3х – 5y = 15
у = 2х + 4
Answers
Answer:
the answer is m equals 3 over 5
Related Questions
Find a in degrees and round to nearest hundreth

Answers
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.
Destiny owns a cake shop and she is working on two wedding cakes this week. The first cake consists of 4 small tiers and 4 large tiers, which will serve a total of 288 guests. The second one includes 3 small tiers and 5 large tiers, which is enough servings for 316 guests. How many guests does each size of tier serve?
A small tier will serve guests and a large tier will serve guests.
Answers
Answer:
small tier: 22large tier: 50Step-by-step explanation:
If cakes of 4 small and 4 large tiers serve 288 guests, and 3 small and 5 large tiers serve 316 guests, you want to know the number of guests served by a tier of each size.
SetupLet 's' and 'l' represent the numbers of guests served by small and large cake tiers, respectively. The first cake serves ...
4s +4l = 288
And the second cake serves ...
3s +5l = 316
SolutionSubtracting 3/4 of the first equation from the second gives ...
(3x +5l) -3/4(4s +4l) = (316) -3/4(288)
2l = 100
l = 50
4s +4(50) = 288 . . . substitute for l in the first equation
4s = 88 . . . . . . . . . . subtract 200
s = 22 . . . . . . . divide by 4
A small tier will serve 22 guests; a large tier will serve 50 guests.

Solve equation by the quadratic formula .list the solution by commas 3m^2+m+13=3 please answer me

Answers
We will have the following:
\(\begin{gathered} 3m^2+m+10=0\Rightarrow m=\frac{-(1)\pm\sqrt{(1)^2-4(3)(10)}}{2(3)} \\ \\ \Rightarrow x=-\frac{1}{6}-\frac{\sqrt{119}}{6}i \\ \\ and \\ \\ \Rightarrow x=-\frac{1}{6}+\frac{\sqrt{119}}{6}i \end{gathered}\)From this, we can see that the function has no solution in the real numbers and the solutions are:
\(-\frac{1}{6}-\frac{\sqrt{119}}{6}i,-\frac{1}{6}+\frac{\sqrt{119}}{6}i\)A factory that makes statues is trying to maximize its income. Their two primary products are the Liberty and David statues. Each Liberty requires 18 minutes of machine time to rough cut the shape and 36 minutes of artist time to finish the details. The David requires 27 minutes on the machines and 18 minutes with the artist's hand. The factory is limited each day to 162 minutes of machine time and 216 minutes of artist time. Both use 7 pounds of stone, and the factory has 49 pounds of stone available per day. If each Liberty brings in a profit of sixty-three dollars, and each David brings in ninety-six dollars, how many statues of each type should the factory make each day?
Constraints:
⎧
⎪
⎨
⎪
⎩
18
L
+
27
D
≤
162
36
L
+
18
D
≤
216
7
L
+
7
D
≤
49
Objective:
Income =
63
L
+
96
D
Answers
Optimizing function describes the minimum or maximum output from the function.
The factory should make 3 David statues and 4.5 Liberty statues
The constraints and the objective function are given as:
\(\mathbf{18L + 27 D \le 162}\)
\(\mathbf{36L + 18 D\le 216}\)
\(\mathbf{7L + 7D \le 49}\)
\(\mathbf{Objective:\ Income = 63L+ 96D}\)
We start by plotting the graphs of the inequalities, where L is represented on the vertical axis, and D on the horizontal axis
From the graph, the only optimal point is: D = 3 and L = 4.5
Hence, the factory should make 3 David statues and 4.5 Liberty statues
Read more about optimizing functions at:
https://brainly.com/question/11206462

Two planes, which are 2760 miles apart, fly toward each other. Their speeds differ by 40 mph. If they pass each other in 4 hours, what is the speed of each?
Answers
Answer:
3x-x+2=4
Step-by-step explanation:
i ain readin allat !!
The speed of the slower plane is 325 mph and the speed of the faster plane is 365 mph.
Explanation:This is a classic problem of relative speed. The two planes are moving toward each other, so their effective speed is the sum of their individual speeds. If we denote the slower plane's speed as x mph, then the faster plane's speed would be x + 40 mph. As they pass each other in 4 hours, we get the equation: 4*(x + x + 40) = 2760.
Solving this equation, we first simplify it to 2x + 40 = 690. Subtracting 40 from both sides gives us 2x = 650. Dividing both sides by 2 yields x = 325 mph, which is the speed of the slower plane, and the faster plane's speed is x + 40 = 365 mph.
Learn more about Relative Speed here:https://brainly.com/question/32038972
#SPJ2
The scale drawing of a room to be 3 inches by 4 1/2 inches. carpet, which is $15.00 per square yard, is to be installed in the room
Answers
Answer:
$202.5
Step-by-step explanation:
13.5 sqyd area
13.5 x 15= $202.5
The two points that define the latus rectum are?

Answers
Answer:
(a, 2a), and (a, -2a)
Find the present value of an annuity which pays ` 200 at the end of each 3 months for 10 years assuming
money to be worth 5% converted quarterly?
(a) ` 3473.86
(b) ` 3108.60
(c) ` 6265.38
(d) None of thes
Answers
The present value of the annuity is approximately `7032.08. The correct answer is option (d) None of these.
To find the present value of an annuity, we can use the formula:
PV = PMT * (1 - (1 + r)^(-n)) / r
Where PV is the present value, PMT is the periodic payment, r is the interest rate per period, and n is the number of periods.
In this case, the periodic payment is `200, the interest rate is 5% (or 0.05) converted quarterly, and the number of periods is 10 years, which equals 40 quarters.
Plugging in these values into the formula, we get:
PV = 200 * (1 - (1 + 0.05)^(-40)) / 0.05
Simplifying the equation, we find:
PV ≈ 200 * (1 - 0.12198) / 0.05
PV ≈ 200 * 0.87802 / 0.05
PV ≈ 35160.4 / 0.05
PV ≈ 7032.08
Therefore, the present value of the annuity is approximately `7032.08.
None of the provided answer options (a), (b), or (c) match this result. The correct answer is (d) None of these.
For more such questions on annuity
https://brainly.com/question/25792915
#SPJ8
I understand the lower and upper class limits but there are only one number but I don't know what to do

Answers
The class mark of the modal class is: 25
How to solveFrom the given histogram, the following Frequency Distribution is obtained:
Class Interval Mid point Frequency
625-675 650 3
676-726 701 5
727 - 777 752 7
778 - 828 803 8
829 - 879 854 6
880 - 930 905 2
931 - 981 956 0
982 - 1032 1007 1
b. To find the lower class limit of the first class:
First class: 625
c. The upper limit of the first class is:
First class: 676
The class mark of the modal class is:
The modal class is: 803
The class mark is upper limit + lower limit/2
Thus, 828-778/2
=> 50/2
The class mark of the modal class is: 25
Read more about class mark here:
https://brainly.com/question/19473137
#SPJ1
Consider a sample with six observations of 15, 16, 12, 8, 6, and 9. Compute the z-scores for each sample observation.
Sample observation. z-scores
15
16
12
8
6
9
Answers
Answer:
1 ; 1.25 ; 0.25 ; - 0.75 ; - 1.25 ;- 0.5
Step-by-step explanation:
Given the sample observations : 15, 16, 12, 8, 6, 9
Zscore for each sample Observation :
Zscore = (x - mean) / standard deviation
(15 + 16 + 12 + 8 + 6 + 9) / 6 = 11
Mean value (m) = 11
Standard deviation (s) = 5
Sqrt[(x - m)^2 / (n - 1)]
[(15-11)^2 + (16-11)^2 + (12-11)^2 + (8-11)^2 + (6-11)^2 + (9-11)^2] / (6 - 1)
= 80/5 = 16
Sqrt(16) = 4
Zscore = (x - mean) / standard deviation
x = 15
Zscore = (15 - 11) / 4 = 1
x = 16
Zscore = (16 - 11) / 4 = 1.25
x = 12
Zscore = (12 - 11) / 4 = 0.25
x = 8
Zscore = (8 - 11) / 4 = - 0.75
x = 6
Zscore = (6 - 11) / 4 = - 1.25
x = 9
Zscore = (9 - 11) / 4 = - 0.5
the ruiz family is exchanging euros for us dollars the exchange rate is 1 euro 1.35261
Answers
Answer:so what is the question
Step-by-step explanation:
PLSSSS I NEED HELP
Evaluate 35a when a=7.
Answers
Answer:
\(35x \\ 35 \times 7 = 245\)
Answer:
245
Step-by-step explanation:
All you have to do is replace a with 7.
So, 35a=35*7= 245
Two buildings are 18 m part. The shorter building is 12 m high while the taller one is 19 m high. Find the distance, x m between the top of the buildings.
Answers
The distance between the tops of the buildings is 28.5 meters.
To find the distance between the top of the buildings, we can use the concept of similar triangles.
Let's denote the height of the shorter building as "a" (12 m) and the height of the taller building as "b" (19 m). The distance between the buildings can be denoted as "c" (18 m), and the distance between the top of the buildings as "x" (which we need to find).
We can set up a proportion based on the similar triangles formed by the buildings:
a/c = b/x
Substituting the known values:
12/18 = 19/x
To find "x," we can cross-multiply and solve for "x":
12x = 18 * 19
12x = 342
x = 342/12
x = 28.5 m
Therefore, the distance between the tops of the buildings is 28.5 meters.
for such more question on distance
https://brainly.com/question/12356021
#SPJ8
which one is bigger? 3/8 or 2/8
Answers
Answer:
3/8 because 3 is bigger than 2.
3 of anything is bigger than 2 of the same thing.
Ralph Chase plans to sell a piece of property for $150000. He wants the money to be paid off in two ways a - short-term note at 11% interest and a long-term note at 8% interest. Find the amount of each note if the total annual interest paid is $15200
.
Answers
Answer:
Amount on 11% note = $106,666.67
Amount on 8% note = $43,333.33
Step-by-step explanation:
Let the amount for the short-term note at 11% interest be x.
Thus, the amount for the short-term note at 8% interest will be (150000 - x)
Now we are told that the total interest paid is $15,200.
Thus;
0.11x + 0.08(150000 - x) = 15200
0.11x + 12000 - 0.08x = 15200
Rearranging gives;
0.03x = 15200 - 12000
0.03x = 3200
x = 3200/0.03
x = $106666.67
Thus, amount for 8% note = $150000 - $106666.67 = $43,333.33
the difference between a two-digit number and that number reversed is 18. What could that number be. List all possibility's.
Answers
9514 1404 393
Answer:
20, 31, 42, 53, 64, 75, 86, 97
Step-by-step explanation:
The difference of 18 means the difference of digits is 18/9 = 2. Since the number you seek is the larger number, the 10s digit will be 2 more than the 1s digit. Possible numbers are ...
20, 31, 42, 53, 64, 75, 86, 97
_____
If t and o are the tens and ones digits respectively, the relation you seek is ...
(10t +o) -(10o +t) = 18
9(t -o) = 18
t - o = 2 . . . . as above
Since both t and o must be single digits, the minimum will be t=2, o=0, and the maximum will be t=9, o=7.
Answer:
10a+b=10b+a-18
9a+9b = -18
9(a+b) = -18
a+b = 18/9
a + b =2
Step-by-step explanation:
X+1 is greater than or equal to 3 or 4/3x is greater than -8. Solve, graph, and write the solution to the following inequality in interval notation.
Answers
The solution of the inequalities is x ≥ 2 or x > -6. The interval notation of the solution of the following inequality is (-6, ∞).
What is interval notation?In mathematics, a range can be conceived of as an interval. It describes a collection of real numbers that starts at one and ends at another. This interval could or might not have its beginning and ending points. Interval notation is a method of representing an interval technically. Interval notation, as its name indicates, is a way to mark or depict an interval that contains a subset of real numbers. A continuous interval of one subset of real numbers or the union of two subsets of real numbers can both be expressed using interval notation. Whether the endpoints are included (a closed interval) or omitted is also indicated by the notation (an open interval).
Given that,
x + 1 ≥ 3 or
4/3x > -8
The solution of the inequalities are:
x + 1 ≥ 3 or 4/3x > -8
x ≥ 2 or x > -6
The system thus consists of all the elements that are present in the system of the equations.
The interval notation of the solution of the following inequality is (-6, ∞).
To graph the equation equate different values of x and obtain values of y and plot them on the graph.
Learn more about interval notation here:
https://brainly.com/question/17249352
#SPJ1
There are 5 white balls, 8 red balls, 7 yellow balls and 4 green balls in a container. A ball is chosen at random. What is the probability of choosing neither white nor green
Answers
Answer: 5/8
Step-by-step explanation:
i just added all of them & took out the white and green balls ......... oh and i also simplified itAnswer:
The probability is 5/8
Step-by-step explanation:
First, we must add all the numbers together. 5 + 8 + 7 + 4 = 24. Now, let's add the white balls and green balls. 5 + 4 = 9. Therefore, the probability of choosing a white or green ball is 9/24 which also equals 3/8. To find out the probability of NOT choosing white or green, we must subtract 9 from 24. 24 - 9 = 15. So, the probability of choosing neither the white or green balls equals 15/24 which also equals 5/8.
Hope this helps!!
what is 4*6 i need help
Answers
3x^3-2x^2+7x+9 divided by x^2-3x
Answers
The quotient is 3x + 7, and the remainder is (28x + 9) / (x^2 - 3x).
What is Division?A division is a process of splitting a specific amount into equal parts.
We have to find 3x³-2x²+7x+9 divided by x²-3x
3x³-2x²+7x+9 is the dividend and x²-3x is the divisor.
The steps to solve this are given below.
Step 1: Take the first digit of the dividend from the left. Check if this digit is greater than or equal to the divisor.
Step 2: Then divide it by the divisor and write the answer on top as the quotient.
Step 3: Subtract the result from the digit and write the difference below.
Step 4: Bring down the next digit of the dividend (if present).
Step 5: Repeat the same process.
Hence, the quotient is 3x + 7, and the remainder is (28x + 9) / (x^2 - 3x).
To learn more on Division click:
https://brainly.com/question/21416852
#SPJ9

If triangle VWX, the measure of angle X=90°, the measure of angle is W=31°, and XV = 8.4 feet. Find the length of WX to the nearest tenth of a foot.
Answers
To find the measure of a side in a right triangle as given (have a angle of 90º) you use the trigonometric function. Use the value of the angle W=31º
\(\tan \alpha=\frac{opposite}{adjacent}\)The opposite side of angle W is XV and the adjacent side is y:
\(tan31=\frac{8.4ft}{y}\)Use this equation to find the value of side WX (y):
\(\begin{gathered} y\cdot\tan 31=8.4ft \\ y=\frac{8.4ft}{\tan 31} \\ \\ y=13.979ft \end{gathered}\)Then, side WX is 14.0 ft (rounded to the nearest tenth)
Choose the fraction that is NOT equivalent to 2/2?
A.1/1
B.2/1
C.3/3
D.4/4
Answers
Answer:
B 2/1
Step-by-step explanation:
2/2=1
3/3=1
4/4=1
and 2/1=2
what is the property of 3x(5x7)=(3x5)7
Answers
The property you are referring to is called the associative property of multiplication. According to this property, when multiplying three numbers, the grouping of the numbers does not affect the result. In other words, you can change the grouping of the factors without changing the product.
In the equation you provided: 3x(5x7) = (3x5)7
The associative property allows us to group the factors in different ways without changing the result. So, whether we multiply 5 and 7 first, or multiply 3 and 5 first, the final product will be the same.
Orly uses 3 cups of raisins for every 10 cups of trail mix she makes. How many cups of trail mix will she make if she uses cups of raisins?
Answers
The total 'x' number of cups of trail mix Orly uses c cups of raisins, she will make 10c / 3 cups of trail mix.
Orly uses 3 cups of raisins for every 10 cups of trail mix,
Which means that the ratio of cups of raisins to cups of trail mix is 3:10.
let us consider x be the number of cups of trail mix
and c be the number of cups of raisins.
We can set up a proportion to solve for the number of cups of trail mix,
⇒ 3/10 = c/x
To solve for x, we can cross-multiply and simplify,
⇒ 3x = 10c
⇒ x = 10c / 3
Therefore, if Orly uses c cups of raisins, she will make 10c / 3 cups of trail mix.
learn more about cups here
brainly.com/question/2487851
#SPJ1
how you define pricing?
Answers
Answer:
the cost per or per liter,one kilogram,one pound e.t c is called pricing in mathematics
Answer:
Definition: Price is the value that is put to a product or service and is the result of a complex set of calculations, research and understanding and risk taking ability. A pricing strategy takes into account segments, ability to pay, market conditions, competitor actions, trade margins and input costs, amongst others.
Help please:)
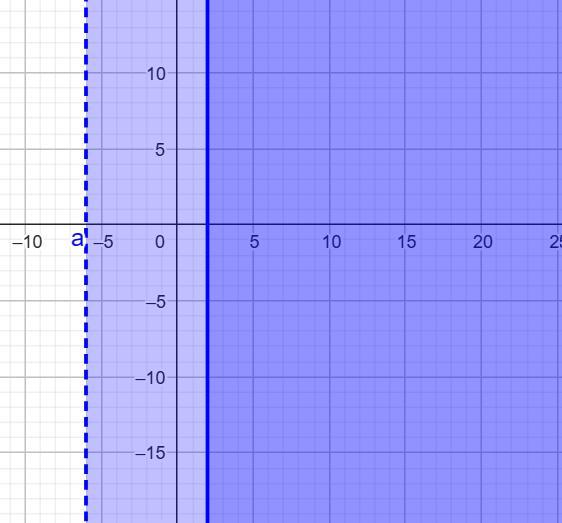
Graph the equation by plotting points.
X=4
Answers
Answer:
(4,0)
Step-by-step explanation:
You basically are plotting a point on the positive number 4 on the x line. Since they're only asking for an X and not a Y, you'd leave it as (4,0). Hope this helps!
Evaluate the expression and write your answer in the form a + bi. 1) (2-6i)+(4+2i)2) (6+5i)(9-2i)3) 2/(3-9i)4) (3 − 5i)(7 − 2i)
Answers
Answer:
Step-by-step explanation:
Given the following complex numbers, we are to expressed them in the form of a+bi where a is the real part and b is the imaginary part of the complex number.
1) (2-6i)+(4+2i)
open the parenthesis
= 2-6i+4+2i
collect like terms
= 2+4-6i+2i
= 6-4i
2) (6+5i)(9-2i)
= 6(9)-6(2i)+9(5i)-5i(2i)
= 54-12i+45i-10i²
= 54+33i-10i²
In complex number i² = -1
= 54+33i-10(-1)
= 54+33i+10
= 54+10+33i
= 64+33i
3) For the complex number 2/(3-9i), we will rationalize by multiplying by the conjugate of the denominator i.e 3+9i
= 2/3-9i*3+9i/3+9i
=2(3+9i)/(3-9i)(3+9i)
= 6+18i/9-27i+27i-81i²
= 6+18i/9-81(-1)
= 6+18i/9+81
= 6+18i/90
= 6/90 + 18i/90
= 1/15+1/5 i
4) For (3 − 5i)(7 − 2i)
open the parenthesis
= 3(7)-3(2i)-7(5i)-5i(-2i)
= 21-6i-35i+10i²
= 21-6i-35i+10(-1)
= 21-41i-10
= 11-41i
Simplified form of the given expressions will be,
1). 6 - 4i
2). 64 + 33i
3). \(\frac{1}{15}+\frac{1}{5}i\)
4). \(\frac{31}{53}-\frac{31}{53}i\)
1). In a complex number (a + bi),
a = Real part of the complex number
bi = Imaginary part
Expression given in the question → (2 - 6i) + (4 + 2i)
Rule to solve the given expression,
"Add real part and imaginary part of two complex numbers separately"
(2 - 6i) + (4 + 2i) = (2 + 4) + (-6i + 2i)
= 6 + (-4i)
= 6 - 4i
Therefore, simplified form of the given expression will be (6 - 4i).
2). Given expression → (6 + 5i)(9 - 2i)
Rule to solve the expression → i² = -1
(6 + 5i)(9 - 2i) = 6(9 - 2i) + 5i(9 - 2i)
= 54 - 12i + 45i - 10i²
= 54 - 12i + 45i + 10 [Since, i² = -1]
= (54 + 10) + (45i - 12i)
= 64 + 33i
Therefore, simplified form of the given expression will be (64 + 33i).
3). Given expression → \(\frac{2}{3-9i}\)
Multiply numerator and denominator with the conjugate of (3 - 9i) to convert the expression into (a + bi).
\(\frac{2}{3-9i}= \frac{2(3+9i)}{(3-9i)(3+9i)}\)
\(=\frac{2(3+9i)}{3^2-(9i)^2}\)
\(=\frac{6+18i}{9-81(-1)}\)
\(=\frac{6+18i}{9+81}\)
\(=\frac{6+18i}{90}\)
\(=\frac{6(1+3i)}{90}\)
\(=\frac{1}{15}+\frac{1}{5}i\)
Therefore, simplified form of the given expression will be \(\frac{1}{15}+\frac{1}{5}i\)
4). Given expression → \(\frac{(3-5i)}{(7-2i)}\)
Multiply numerator and denominator with the conjugate of the denominator.
\(\frac{(3-5i)}{(7-2i)}=\frac{(3-5i)(7+2i)}{(7-2i)(7+2i)}\)
\(=\frac{3(7+2i)-5i(7+2i)}{7^2-(2i)^2}\)
\(=\frac{21+4i-35i-10i^2}{49-4(-1)}\)
\(=\frac{21-31i+10}{53}\)
\(=\frac{31-31i}{53}\)
\(=\frac{31}{53}-\frac{31}{53}i\)
Therefore, simplified form of the given expression will be \(\frac{31}{53}-\frac{31}{53}i\).
Learn more,
https://brainly.com/question/2571267
What is the constant of proportionality in the equation y=5/4x
Answers
The constant of proportionality in the equation is 5/4
What is constant of proportionality?The constant connecting two given numbers in what is known in a proportional relationship is the constant of proportionality.
The constant of proportionality may also be referred to as the constant ratio, constant rate, unit rate, constant of variation, or even the rate of change.
In the problem, y = 5/4x
The constant term 5/4 as used in the equation is used t multiply the input x values to get the out put y values
The term helps in relating x to y
Learn more about constant of proportionality at:
https://brainly.com/question/27598477
#SPJ1
Estimate how much a paramedic will make over 30 years
Answers
Answer:
The salary of a paramedic can vary depending on several factors such as location, experience, and employer. According to the Bureau of Labor Statistics, the median annual wage for paramedics and EMTs was $36,650 in May 2020.
Assuming a constant annual income of $36,650 over 30 years, the estimated total income for a paramedic would be:
$36,650 x 30 = $1,099,500
However, it is important to note that this is just an estimate and does not take into account potential salary increases, promotions, or changes in the job market.
It takes a bear 9 more days to eat a barrel of honey alone than it takes the bear and a second bear to eat the barrel of honey together. It takes the first bear 7 fewer days to eat a barrel of honey alone than it takes the second bear to eat a barrel of honey alone. In how many days can the two bears eat a barrel of honey together?
Answers
Answer:
it takes the bears 12 days to eat honey together.
Step-by-step explanation:
1/x+9+1/x+16=1/x
(solve this using cross multiplication)
= x^2 = 144
x=12
The number of days that it takes for both of the considered bears to eat a barrel of honey together is 12 days.
How are number of people to time needed to complete a task related?More people to do a task means less time it will take.
Less people to do a task means more time it will take.
Thus, they are inversely related.
We can define a constant as "Manpower" needed for doing that specific work.
Each worker has his/her own strength. That strength is applied per unit of time.
Let we define:
Manpower needed for a work = time taken for that work × strength used for that work per unit of time
(we used multiplication as it represents linear use of strength to finish the task, so using that strength for a finite units of time means you stacked up your strengths that many times to finish that work)
Here, we have:
Instead of people, here we consider bears.Work in consideration = eating honey out of a considered barrel (assuming all barrels considered will have same amount of honey)Assume that:
Strength of first bear (call it bear A) for eating honey = S per day (as unit of time is a day here).Strength of second bear (call it bear B) for eating honey = T per dayManpower the work needs be M (assume)Time needed by bear A to complete the work = 'x' daysTime needed by bear B to complete the work = 'y' days.Then, we get:
Manpower needed for a work = time taken for that work × strength used for that work per unit of time
\(M = x \times S\\M = y \times T\)
If bear A and bear B both do the work together, then their strenghts will add up.
That means, the combined strength would be S + T per day
The manpower the work needs is still M, therefore, the time needed is:
\(M = \text{Time needed} \times (S + T)\\\\\text{Time needed} = \dfrac{M}{S+T}\)
This is the time needed for both bears to do the work together.
Also, it is given that:
It takes a bear 9 more days to eat a barrel of honey alone than it takes the bear and a second bear to eat the barrel of honey together.
or
Time needed by bear A to do work = 9 + time needed by both bears to do the work
or
\(x = 9 + \dfrac{M}{S + T}\)
Also, it is given that:
It takes the first bear 7 fewer days to eat a barrel of honey alone than it takes the second bear to eat a barrel of honey alone.
or
Time taken by bear A to do the work = Time taken by bear B for that work - 7 days
or
\(x = y - 7\)
Thus, we got these equations:
\(M = S \times x\\M = T \times y\\\\x = \dfrac{M}{S + T} +9\\\\x = y - 7\)
call them first, second, third and fourth equation as per their ordering.
From the first and second equation, we get:
\(S = \dfrac{M}{x}\\\\T = \dfrac{M}{y}\)
Putting these values in the third equation, we get:
\(x = \dfrac{M}{M/x + M/y} + 9\\\\\\x = \dfrac{xy}{x+y} + 9\\\\(x-9)(x+y) = xy\\x^2 -9x -9y + xy = xy\\x^2 -9x = 9y\)
From the fourth equation, we know that:
\(x = y - 7\)
or \(y = x +7\)
Putting this value of y in the equation \(x^2 -9x = 9y\), we get:
\(x^2 -9x = 9(x+7)\\x^2 -9x = 9x + 63\\x^2 -18x -63 =0\\\\x^2 -21x + 3x -63 = 0\\x(x-21) + 3(x - 21) = 0\\(x+3)(x-21) = 0\\(x+3) = 0, (x-21) = 0\\x = -3, x = 21\)
'x' represents time in number of days. So it cannot be negative.
Thus, the value of x obtained is 21.
Also, we need: Time needed for both the bears to do the work together.
This time is the value of \(\dfrac{M}{S+T}\), which is equal to \(x - 9\) days (from the third equation)
Thus, the time needed for both the bears to do the work together = \(x-9 = 21-9 = 12 \; \rm days\)
Thus, the number of days that it takes for both of the considered bears to eat a barrel of honey together is 12 days.
Learn more about work and time here:
https://brainly.com/question/1063042
#SPJ2