72. Shoe Sales On Saturday night, the manager of a shoe store evaluates the receipts of the previous week's sales. Two hundred and forty pairs of two different styles of tennis shoes were sold. One style sold for $66.95 and the other sold for $84.95. The total receipts were $17,652. The cash register that was supposed to record the number of each type of shoe
sold malfunctioned. Can you recover the information? If so, how many shoes of each type were sold?
Answers
Answer:
To solve this problem, we can use a system of equations. Let x be the number of shoes sold at $66.95 and y be the number of shoes sold at $84.95. We know that:
x + y = 240 (because 240 pairs of shoes were sold in total)
66.95x + 84.95y = 17,652 (because this is the total amount of money earned from shoe sales)
To find the number of each type of shoe sold, we can use substitution method, by solving one equation for one variable and substituting that expression into the other equation.
We can solve the first equation for y:
y = 240 - x
Then we can substitute this expression into the second equation and solve for x:
66.95x + 84.95(240 - x) = 17,652
66.95x + 21,068 - 84.95x = 17,652
-18x = -3,416
x = 176
So, 176 pairs of shoes were sold at $66.95. To find the number of shoes sold at $84.95, we can substitute this value of x into the first equation:
y = 240 - 176 = 64
So, 64 pairs of shoes were sold at $84.95.
In conclusion, we can recover the information and the manager can know that 176 pairs of shoes were sold at $66.95 and 64 pairs of shoes were sold at $84.95.
Related Questions
abcdefghijklmnopqrstuvwxyz
Answers
Answer: ??
Step-by-step explanation:
Answer:
Step-by-step explanation:
huh
Which expression is equivalent to 6–3,
o 63
O 36
O 36
3
o
O
ool

Answers
Answer:
\(\huge\underline{\red{A}\blue{n}\pink{s}\purple{w}\orange{e}\green{r} -}\)
a basic rule of exponents and powers states that if the power / exponent of the given base is a negative integer , we can reciprocate the base and change the power from negative to positive!
According to this rule ,
\(6 { }^{ - 3} \: can \: be \: written \: as \\ \\ \dashrightarrow \: (\frac{1}{6} ){}^{3} \)
therefore , 4th option is correct !
hope helpful :)
I need help
please help

Answers
9514 1404 393
Answer:
see attached
Step-by-step explanation:
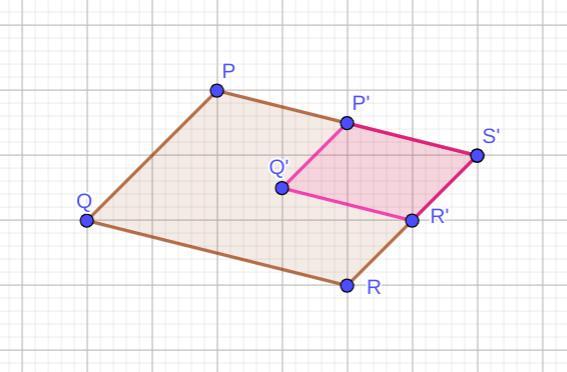
Dilation by a factor of 1/2 about point S means each point moves to a position half as far from S as it was to begin with. Point S remains invariant. (Point S and S' are the same point.)
Rick deposited $1500 in a savings account that earns 6% interest for 4 years. How much money is in his account at the end of the 4 years?
Answers
Answer:
$5820
Step-by-step explanation:
1500*6%=90 per month
90*(48months=4yrs)=4320
1500+4320=5820
Find the length of the hypotenuse of the right triangle. Use pencil and paper. Explain how you can interpret the Pythagorean Theorem using the areas of squares. A right triangle has a vertical leg labeled 7 and a horizontal leg labeled 24. The hypotenuse is labeled c. 24 7 c. The length of the hypotenuse is
Answers
Answer: The length of the hypotenuse is 25
Step-by-step explanation:
Hi, to answer this question we have to apply the Pythagorean Theorem:
c^2 = a^2 + b^2
Where c is the hypotenuse of the triangle (the longest side) and a and b are the other legs of the triangle (vertical and horizontal leg)
Replacing with the values given:
c^2 = 7^2 + 24^2
c^2 = 49+576
c^2 = 625
c = √625
c = 25
Feel free to ask for more if needed or if you did not understand something.
Find the sum: 34∑n=1(-17+8k)

Answers
The summation is 4182
suppose you randomly color the edges of the complete graph on 16 vertices with red and blue. what is the expected number of blue edges? suppose you randomly color the edges of the complete graph on 16 vertices with red and blue. what is the expected number of blue edges?
Answers
A complete graph on 16 vertices has a total of C(16, 2) edges, where C(n, k) denotes the binomial coefficient or the number of ways to choose k items from a set of n items. Here, n = 16 and k = 2. We can compute C(16, 2) as follows:
C(16, 2) = 16! / (2! * (16 - 2)!)
= 16! / (2! * 14!)
= (16 * 15) / 2
= 120
So, the complete graph on 16 vertices has 120 edges.
Now, let's calculate the expected number of blue edges. Each edge has a probability of 1/2 of being colored blue, as there are two possible colors: red and blue. To find the expected number of blue edges, we simply multiply the total number of edges by the probability of an edge being blue:
Expected number of blue edges = Total edges * Probability of an edge being blue
= 120 * (1/2)
= 60
Therefore, the expected number of blue edges in the complete graph on 16 vertices when randomly coloring the edges with red and blue is 60.
To learn more about binomial coefficient : brainly.com/question/31229700
#SPJ11
Use the given marginare, confidence level and population standard deviation, σ, to find the minimum samples required to estimate an unknown population mea, μ
Margin of error 12 inches, confidence level 90%, σ = 24 inches
A confidence level of 90% requires a minimum sample size of ___ (Round up to the nearest integer)
Answers
a confidence level of 90% requires a minimum sample size of 44 Rounded up to the nearest integer.
The margin of error, confidence level, and population standard deviation, σ, is provided in the question, and we need to determine the minimum sample size required to estimate an unknown population mean, μ. We'll use the following formula to solve the problem:
Where,n = Sample size requiredz = Z-score that corresponds to the given confidence levelE = Margin of errorσ = Population standard deviationIn the given question, the margin of error is 12 inches, confidence level is 90%, and the population standard deviation, σ, is 24 inches.
To get the Z-score corresponding to a 90% confidence level, we must use a z-table, which gives a value of 1.645.
Simplifying the above equation, we get,
We must always round up the minimum sample size to the nearest integer because it is impossible to have a fraction of a sample size. Thus, the minimum sample size required to estimate an unknown population mean is 44. Hence, a confidence level of 90% requires a minimum sample size of 44 (Rounded up to the nearest integer).
To know more about selling price visit:
https://brainly.com/question/29109312
#SPJ11
plzzzzz help need answer by 5 mins plzzzz

Answers
Answer:
D
Step-by-step explanation:
Answer:
Its D
Step-by-step explanation:
all other answers are wrong because you will soon have to multiply a negative with a negative thus making it a positive.
alex and ben go to a cafe with some friends.
alex buys 4 cups of coffee and 3 cups of tea. he paid a total of £6.95.
Ben buys 5 cups of coffee and 2 cups of tea. He pays a total of £7.20.
work out the total cost of each cup of coffee in the cost of each cup of tea
Answers
Answer:
Step-by-step explanation:
Assume the cost for a cup of coffee is x and the cost for a cup of tea is y.
For Alex: 4x+3y=6.95
For Ben 5x+2y=7.20
Then multiply Alex's cost by 2 and Ben's by 3 to cancel y.
8x+6y=13.90
15x+6y=21.60
Equation 2 minus equation 1 would be
15x+6y-(8x+6y)=15x+6y-8x-6y=7x
21.60-13.90=7.70
7x=7.70
Then x=1.10 and plugging it one of the equations,
y= 0.85
A cup of coffee costs 1.10 pounds and A cup of tea is 0.85 pounds
:)
"Find the area and the circumference of a circle with diameter of 8m"

Answers
Radius = diameter/2 = 8/2 = 4m
Area of a circle = pi x r^2 = pi x 4^2 = 16pi m^2 ( exact area) or 50.27 m^2
Circumference = pi x diameter = 8pi m ( exact) or 25.12 m
Answer:
C = 25.12 A = 50.24
Step-by-step explanation:
Circumference formula = dπ
Area formula = πr^2
Circumference:
Plug in:
8π
8 × 3.14 = 25.12
Area:
8/2 = 4
r = 4
Plug in:
πr^2
π4^2
16π
16 × 3.14 = 50.24
Hope this helped.
Explain how to convert 44.0 gallons to liters.
Answers
It is instructed that we change 44.0 gallons to liters. One gallon is one unit of volume. A gallon is equivalent to 3.785 liters.
3.785411784 litres make to one US gallon. 4 quarts, 8 pints, or 128 fluid ounces make up a gallon. In American measurements, a gallon is equivalent to 3.785 litres, 128 fluid ounces, 4 quarts, 8 pints, or 16 cups. A gallon's volume is about equivalent to 3.78541 litres. Thus, a gallon is more than three litres. A gallon of one liquid could weigh differently than a gallon of another. As one imperial gallon is equal to 4.54609 litres, it takes up space that is nearly 4,546 cubic centimetres (roughly a 16.5cm cube). An average glass holds eight ounces. So, 16 eight-ounce glasses of water make up a gallon.
44.0 gallons to 3.785 liters.
Learn more about gallon here
https://brainly.com/question/28274339
#SPJ4
Find f(a),f(a+h), and the difference quotient
h
f(a+h)−f(a)
, where h
=0
f(x)=
x+7
x
f(a)=
f(a+h)=
Answers
We have `f(a) = (a+7)/a`, `f(a+h) = (a+h+7)/(a+h)`, and the difference quotient is `(h(a+7))/(ah+h^2)`.
Given a function `f(x)` is defined by `f(x) = (x+7)/x`.
We need to find `f(a)`, `f(a+h)`, and the difference quotient `(f(a+h)-f(a))/h` where `h≠0`.
Solution:
`f(x) = (x+7)/x`
At `x=a`, we have
`f(a) = (a+7)/a`.
At `x = a + h`,
we have `
f(a+h) = [(a+h)+7]/(a+h)`.
So,
`f(a+h) = (a+h+7)/(a+h)`.
Now,
`f(a+h)−f(a)` is `[(a+h)+7]/(a+h) − (a+7)/a`.
LCM of `(a+h)` and `a` is `a(a+h)`.
So, we get `f(a+h)−f(a)` as `(a+h)(a+7)−a(a+h+7)/a(a+h)`.
On simplification, we have `f(a+h)−f(a)` as `(ah+7h)/(a(a+h))`.
Now, `(f(a+h)−f(a))/h` is `(ah+7h)/(ah+h^2)`.
On simplification, we have `(f(a+h)−f(a))/h` as `(h(a+7))/(ah+h^2)`.
Hence, `f(a) = (a+7)/a`, `f(a+h) = (a+h+7)/(a+h)`, and the difference quotient is `(h(a+7))/(ah+h^2)`.
Given a function `f(x)` is defined by `f(x) = (x+7)/x`. We have found `f(a)`, `f(a+h)`, and the difference quotient `(f(a+h)-f(a))/h` where `h≠0`. Thus, we have `f(a) = (a+7)/a`, `f(a+h) = (a+h+7)/(a+h)`, and the difference quotient is `(h(a+7))/(ah+h^2)`.
To know more about the difference quotient, visit:
brainly.com/question/6200731
#SPJ11
How do you add two negative decimals together?.
Answers
Answer:
-and a -= a positive
Step-by-step explanation:
-8+-9=19
sin−1(sin/6)
cos−1(cos5/4)
tan−1(tan5/6) compute without using a calculator
Answers
Without using a calculator, the trigonometric expressions simplify to:
1. sin^(-1)(sin(θ/6)) = θ/6
2. cos^(-1)(cos(5/4)) = 5/4
3. tan^(-1)(tan(5/6)) = 5/6.
To compute the trigonometric expressions without using a calculator, we can make use of the properties and relationships between trigonometric functions.
1. sin^(-1)(sin(θ/6)):
Since sin^(-1)(sin(x)) = x for -π/2 ≤ x ≤ π/2, we have sin^(-1)(sin(θ/6)) = θ/6.
2. cos^(-1)(cos(5/4)):
Similarly, cos^(-1)(cos(x)) = x for 0 ≤ x ≤ π. Therefore, cos^(-1)(cos(5/4)) = 5/4.
3. tan^(-1)(tan(5/6)):
tan^(-1)(tan(x)) = x for -π/2 < x < π/2. Thus, tan^(-1)(tan(5/6)) = 5/6.
Hence, without using a calculator, we find that:
sin^(-1)(sin(θ/6)) = θ/6,
cos^(-1)(cos(5/4)) = 5/4,
tan^(-1)(tan(5/6)) = 5/6.
To know more about trigonometric expressions refer here:
https://brainly.com/question/12676341#
#SPJ11
An entrance to a building is not wheelchair accessible. The entrance is 6 feet above ground level and 30 feet from the roadway.
b. How can you build a ramp to meet the regulation within the space of 30 feet?
Answers
By utilizing a switchback ramp design, you can meet accessibility regulations within the space of 30 feet for the wheelchair-accessible ramp.
To build a wheelchair-accessible ramp within a space of 30 feet, you can consider using a switchback or zigzag ramp design. This design allows for a longer ramp within a limited space. Here's how you can construct the ramp:
1. Measure the vertical rise: In this case, the entrance is 6 feet above ground level.
2. Determine the slope ratio: To meet accessibility regulations, the slope ratio should be 1:12 or less. This means that for every 1 inch of rise, the ramp should extend 12 inches horizontally.
3. Calculate the ramp length:
Divide the vertical rise (6 feet or 72 inches) by the slope ratio (1:12).
The result is the minimum ramp length required, which is
72 inches x 12 = 864 inches.
4. Consider a switchback design: Since you have a limited space of 30 feet, a straight ramp may not fit. A switchback design allows for a longer ramp by changing direction.
This can be achieved by incorporating platforms or landings at regular intervals.
5. Design the switchback ramp: Divide the total ramp length (864 inches) by the available space (30 feet or 360 inches).
This will determine how many platforms or landings you can incorporate. Ensure that each section of the ramp remains within the slope ratio requirements.
6. Ensure safety and accessibility: Install handrails on both sides of the ramp, with a height of 34-38 inches, to provide support. Make sure the ramp is wide enough (at least 36 inches) to accommodate a wheelchair comfortably.
Know more about the vertical rise
https://brainly.com/question/1904673
#SPJ11
determine the surface area of a right circular cone that has a slant height of 5.8 ft and a diameter of 6.4 ft? round your answer to the nearest whole.

Answers
Answer:
it is 6.4*5.8 brainliest?
Step-by-step explanation:
Determine if 0.1111111111111111...0.1111111111111111... is rational or irrational and give a reason for your answer.
Answers
Answer:
Rational
Step-by-step explanation:
Repeating decimals can be expressed as convergent infinite geometric series, which result in fractions of the form p/q, where p and q are coprime positive integers.
simplify the polynomial expression. (4x^2-2x+7)+(x^2-7x-2)
Answers
Given the following polynomial:
\(\mleft(4x^2-2x+7\mright)+\mleft(x^2-7x-2\mright)\)You can follow the steps shown below in order to simplify it:
Step 1. Remember the Signs rules for multiplication:
\(\begin{gathered} (-)_{}(-)_{}=(+)_{} \\ (-)_{}(+)=(-) \\ (+)(+)=(+) \end{gathered}\)Then, you can rewrite the expression as following:
\(=4x^2-2x+7+x^2-7x-2\)Step 2. Now you must add the like terms (Remember that "like terms" are those terms whose variables are exponents are the same). Then, you get:
\(=5x^2-9x+5\)The answer is:
\(5x^2-9x+5\)How is solving 2x c= d similar to solving 2x 1 = 9 for how are they different? how can you use 2x c= d to solve 2x 1 = 9? free anser
Answers
The value of x is x = 9/4. The equation 2xc = d as follows: 2xc = d2x * 1/2 = 9/22x = 9/2 * 2x = 9/4
The equation 2xc = d and 2x + 1 = 9 are similar in that they are both linear equations and involve the variable x.
However, they are different in that they have different constants and coefficients.
How to use 2xc = d to solve 2x + 1 = 9? To use 2xc = d to solve 2x + 1 = 9, you first need to rewrite 2x + 1 = 9 in the form 2xc = d.
To do this, you need to isolate x on one side of the equation. 2x + 1 = 9
Subtract 1 from both sides2x = 8. Divide both sides by 2x = 4Now, we can write 2x + 1 = 9 as 2x * 1/2 = 9/2.
Therefore, we can see that this equation is similar to 2xc = d, where c = 1/2 and d = 9/2.
We can use this relationship to solve for x in the equation 2xc = d as follows: 2xc = d2x * 1/2 = 9/22x = 9/2 * 2x = 9/4 Therefore, x = 9/4.
To know more about value visit:
brainly.com/question/20532123
#SPJ11
In an interval whose length is z seconds, a body moves (32z+2z 2 )ft. Which of the following is the average speed v of the body in this interval?
Answers
In an interval whose length is z seconds, a body moves (32z+2z 2 )ft;
the average speed v of the body in this interval is 32 + 2z ft/second.
So we need to divide the total distance traveled by the time taken.
To find the average speed of the body in the given interval,
we need to divide the total distance traveled by the time taken.
In this case, the total distance traveled by the body is given as
(32z + 2z²) ft,
and the time taken is z seconds.
Therefore, the average speed v of the body in this interval can be calculated as:
v = total distance / time taken
v = (32z + 2z²) ft / z seconds
Simplifying this expression, we get:
v = 32 + 2z ft/second
So, the average speed of the body in the given interval is 32 + 2z ft/second.
To know more about interval, visit:
https://brainly.com/question/11051767
#SPJ11
Solve the inequality below.
4(x + 3) < 6x – 2
Answers
Answer:
X > 7
Step-by-step explanation:
4(x + 3) < 6x – 2
4x + 12 < 6x -2
-6x -6x
-2x + 12 < -2
-12 -12
-2x < -14
----- -----
-2 -2
x > 7
The < change because it was divided by a negative number
Divide the following. Put
your answer in scientific
notation.
(3.4 X 10^-1) / (4)
Answers
Answer:
8.5 × 10-2
Step-by-step explanation:
I believe this is it
1. use the following normal-form game to answer the questions below. a. identify the one-shot nash equilibrium (10 pts) b. suppose this game is infinitely repeated and the interest rate is 6 percent. can the players achieve payoffs that are better than the one-shot nash equilibrium? what is the payoff? (15 pts)
Answers
One-Shot Nash equilibrium is (A, C).
Yes the players can achieve payoffs that are better than the one-shot Nash equilibrium.
This is due to the fact that player 2 will choose strategy C if player A chooses option A. Player 2 will immediately choose Plan C if Player A chooses Option B. As a result, C becomes the second player's dominant strategy. The optimal decision for player 1 is to choose strategy A if player 2 chooses option C. Player 1 will select A if Player 2 chooses to choose D, making this Player 1's dominant move.
A Nash equilibrium is necessary for matrix reward games with two players if the row chosen is to maximize the payoff for the row player given the column chosen by the column player, and the column, in turn, is to maximize the payoff for the column player given the row chosen by the row player.
Learn more about Nash equilibrium:
brainly.in/question/4220195
#SPJ4
One-Shot Nash equilibrium is (A, C).
Yes, the players can achieve payoffs that are better than the one-shot Nash equilibrium.
This is due to the fact that player 2 will choose strategy C if player A chooses option A. Player 2 will immediately choose Plan C if Player A chooses Option B. As a result, C becomes the second player's dominant strategy. The optimal decision for player 1 is to choose strategy A if player 2 chooses option C. Player 1 will select A if Player 2 chooses to choose D, making this Player 1's dominant move.
A Nash equilibrium is necessary for matrix reward games with two players if the row chosen is to maximize the payoff for the row player given the column chosen by the column player, and the column, in turn, is to maximize the payoff for the column player given the row chosen by the row player.
To learn more about Nash equilibrium visit: brainly.com/question/27578385
#SPJ4
1. Approximate the value of
√
√
Answers
Answer:
\(\sqrt{3} =1.7\\\sqrt{3/48} =0.04\\\sqrt{48} =6.9\\\frac{\sqrt{3} }{\sqrt{48} } =0.25\)
Step-by-step explanation:
I wasn't sure which one you were referring to
the weight of the chocolate and Hershey Kisses are normally distributed with a mean of 4.5338 G and a standard deviation of 0.1039 G
a. For the bell-shaped graph Of the normal distribution of weights of Hershey kisses what is the area under the curve?
b. What is the value of the median?
c. What is the value of the mode?
d. What is the value of the variance?
Answers
For the bell-shaped graph of the normal distribution of weights of Hershey kisses, the area under the curve is 1, the value of the median and mode both is 4.5338 G and the value of variance is 0.0108.
In the given question,
The weight of the chocolate and Hershey Kisses are normally distributed with a mean of 4.5338 G and a standard deviation of 0.1039 G.
We have to find the answer of many question we solve the question one by one.
From the question;
Mean(μ) = 4.5338 G
Standard Deviation(σ) = 0.1039 G
(a) We have to find for the bell-shaped graph of the normal distribution of weights of Hershey kisses what is the area under the curve.
As we know that when the mean is 0 and a standard deviation is 1 then it is known as normal distribution.
So area under the bell shaped curve will be
\(\int\limits^{\infty}_{-\infty} {f(x)} \, dx\)= 1
This shows that that the total area of under the curve.
(b) We have to find the median.
In the normal distribution mean, median both are same. So the value of median equal to the value of mean.
As we know that the value of mean is 4.5338 G.
So the value of median is also 4.5338 G.
(c) We have to find the mode.
In the normal distribution mean, mode both are same. So the value of mode equal to the value of mean.
As we know that the value of mean is 4.5338 G.
So the value of mode is also 4.5338 G.
(d) we have to find the value of variance.
The value of variance is equal to the square of standard deviation.
So Variance = \((0.1039)^2\)
Variance = 0.0108
Hence, the value of variance is 0.0108.
To learn more about normally distribution link is here
https://brainly.com/question/15103234
#SPJ1
the proper way to construct a stem-and-ieaf display for the data set {62,67,68,73, 73, 79,91,94,95,97} is to
Answers
The proper way to construct a stem-and-leaf plot to display the data set {62,67,68,73, 73, 79,91,94,95,97} is to include a stem labeled ‘8’ and enter no leaf on the stem. So, the correct choice is option (b).
A stem and leaf graph is like a special table where each data value is separated into a "stem" (the first number) and a "leaf" (usually the last number). Leaves are sorted in ascending order from left to right. We have a data set with values {62,67,68,73, 73, 79,91,94,95,97}. Now, to construct the stem- leaf plot for our data.
Stem | Leaf
6 | 2 7
7 | 3 3 9
9 | 1 4 5 7
For stem and leaf diagram if some values are not present for some stem, then no leaf should be added to that stem. If we skip that stem than it would distort the shape of distribution of the data.
stem | leaf
6 | 2 7
7 | 3 3 9
8 |
9 | 1 4 5 7
Hence, include a stem labeled 8 and enter no leaves on the stem.
To learn more about stem-and-eaf plot, visit :
https://brainly.com/question/12276901
#SPJ4
Complete question:
The proper way to construct a stem-and-leaf display for the data set {62, 67, 68, 73, 73, 79, 91, 94, 95, 97} is to
a)exclude a stem labeled ‘8
b)include a stem labeled ‘8’ and enter no leaves on the stem.
c) include a stem labeled ‘(8)’ and enter no leaves on the stem.
d) include a stem labeled ‘8’ and enter one leaf value of ‘0’ on the stem.
The solution of m2 − 14m + 49 = 0 is
Answers
Answer:
49/12 or 4 1/12 or 4.083 (all the same answer in different forms)
Step-by-step explanation:
2m-14m+49=0
-12m+49=0
-12m+-49
m=49/12
Answer: m=7
Step-by-step-explanation:
m^2-14m+49=0
(m-7)^2=0
m-7=0
m=7
Help me! thank you so much

Answers
Answer:
Step-by-step explanation:
\(\frac{sinxcos^3x-cos xsin^3x}{cos^42x-sin^42x} \\=\frac{sin x cos x(cos^2x-sin ^2 x)}{(cis^2 2x+sin^2 2x)(cos^2 2x-sin ^22x)} \\=\frac{2sin x cos x cos 2x}{2(1)(cos 4x)} \\=\frac{sin 2x cos 2x}{2 cos 4x} \\=\frac{2 sin 2x cos 2x}{4 cos 4x} \\=\frac{sin 4x}{4 cos 4x} \\=\frac{1}{4} tan 4x\)
what does the slope of a beer's law plot represent
Answers
The slope of a beer's law plot represents that one can quantitatively determine the molar absorptivity of a substance, which is essential for accurately determining concentrations of unknown samples using spectrophotometric methods.
In Beer's law, the relationship between the concentration of a substance and its absorbance is described by the equation A = εbc, where A is the absorbance, ε is the molar absorptivity (also known as the molar absorptivity coefficient), b is the path length of the sample, and c is the concentration of the substance.
When plotting a graph of absorbance versus concentration, the slope of the line represents the molar absorptivity (ε). The molar absorptivity is a constant that reflects the substance's ability to absorb light at a specific wavelength. A higher molar absorptivity indicates that the substance has a greater tendency to absorb light and is more sensitive to changes in concentration.
Conversely, a lower molar absorptivity indicates weaker absorption characteristics.
In summary, by measuring the slope of the Beer's law plot, one can quantitatively determine the molar absorptivity of a substance.
To know more about Beer's law, refer here:
https://brainly.com/question/30762062#
#SPJ11