A 7 inch candle burns at a rate of 2 inches per hour. Which equation represents the
relationship between y, the height of the candle, and x, the number of hours the
candle burns?

The probability of at least one card being a heart is 0.546 or approximately 54.6%.

To solve this problem, we can use the concept of complementary probability, which states that the probability of an event happening is equal to one minus the probability of the event not happening.

The probability of not getting a heart on the first draw is 39/52, since there are 39 non-heart cards out of a total of 52 cards. The same probability applies to the second draw, as the card is replaced. Therefore, the probability of not getting a heart on both draws is (39/52) x (39/52) = 0.454.

Using the complementary probability concept, the probability of at least one card being a heart is 1 - 0.454 = 0.546 or approximately 54.6%.

This means that if we were to repeat this experiment many times, we would expect to get at least one heart card in more than half of the trials.

To learn more about probability click on,

https://brainly.com/question/30874104

#SPJ1

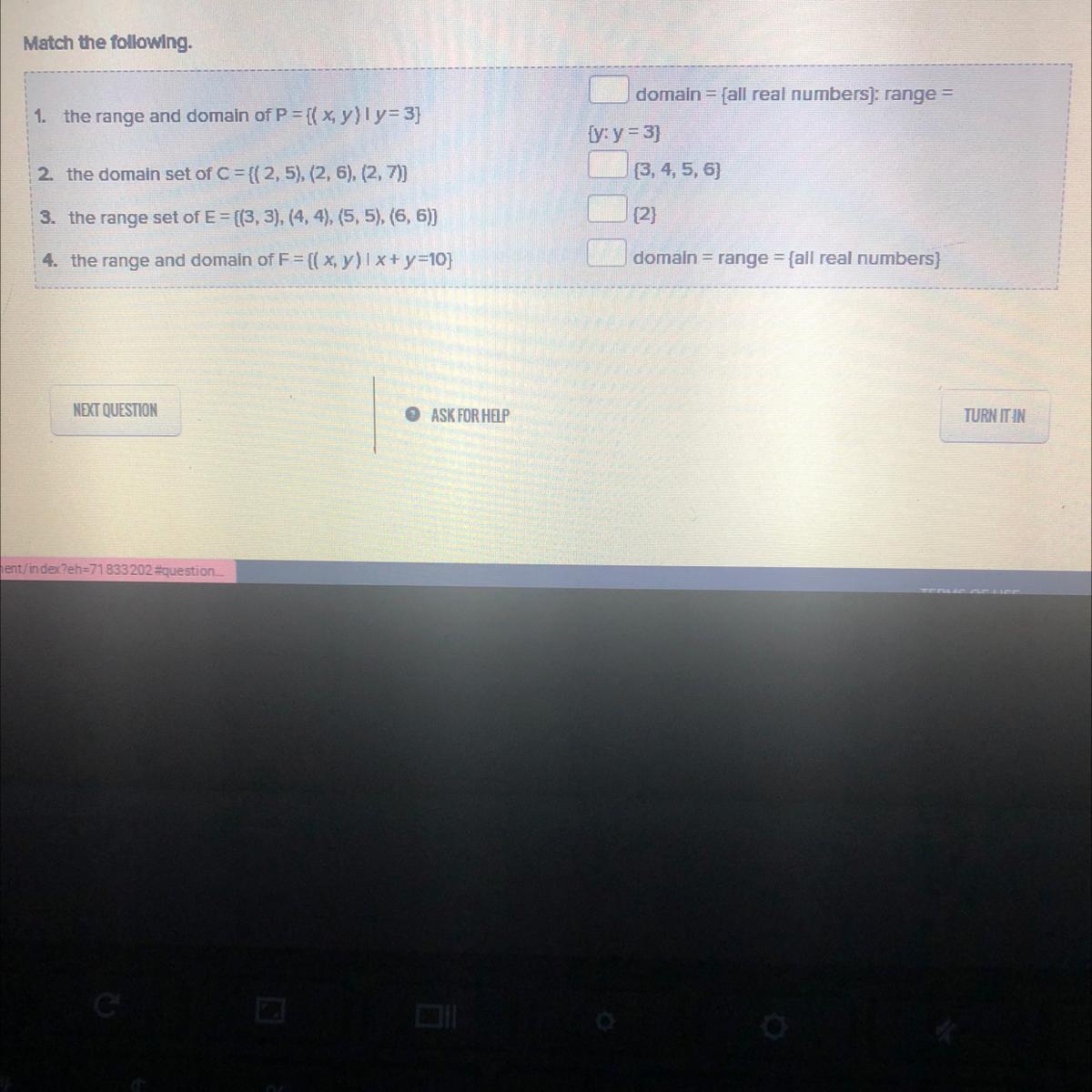
Answer:

Step-by-step explanation:

Domain of a function is defined by the set of x-values (input values) and Range is the set of y-values (output values) of the function.

1). The range and domain of P = {(x, y)| y = 3}

Domain: Set of all real numbers

Range: {y: y=3}

2). The domain set of C = {(2, 5), (2, 6), (2, 7)}

 Domain: {2}

3). The range set of E = {(3, 3), (4, 4), (5, 5), (6, 6)}

  Range: {3, 4, 5, 6}

4). The range and domain set of F = {(x, y)| x + y = 10}

   Domain = Range = {All real numbers}

Answer:

149.6

Step-by-step explanation:

I did the question and got it right

Answer: About 14 liters of gasoline is required.

Step-by-step explanation:

On the map,

1 centimeter= 25 kilometers.

Distance the towns along the highway is 4.5 centimeters.

Actual distance = 4.5 x 25 km

= 112.5 km

Tori's car uses 0.123 liter of gasoline for each kilometer of highway driving.

Total gasoline required = 0.123  x  112.5 km

= 13.8375 liters≈ 14 liters

hence, about 14 liters of gasoline is required.

Answer:

A. f(t) = –16(t – 1)2 + 24

Step-by-step explanation:

The team mascot shoots a rolled T-shirt from a special T-shirt cannon to a section of people in the stands at a basketball game. The T-shirt starts at a height of 8 feet when it leaves the cannon and 1 second later reaches a maximum height of 24 feet before coming back down to a lucky winner. If the path of the T-shirt is represented by a parabola, which function could be used to represent the height of the T-shirt as a function of time, t, in seconds?

A. f(t) = –16(t – 1)² + 24

B. f(t) = –16(t + 1)² + 24

C. f(t) = –16(t – 1)² – 24

D. f(t) = –16(t + 1)² – 24

Answer: The path of the T-shirt is represented by a parabola. The general equation of a parabola is given by y = a(x - h)² + k with a vertex at (h, k).

The height of the t shirt is a function of the time. Given:

A. f(t) = –16(t – 1)² + 24

At time (t) = 0. Therefore:

f(0) = –16(0 – 1)² + 24  = -16 + 24 = 8 feet.

The vertex of the function is at (1, 24). This means at one second, the maximum height is 24 feet.

This is the correct option

B. f(t) = –16(t + 1)² + 24

At time (t) = 0. Therefore:

f(0) = –16(0 + 1)² + 24  = -16 + 24 = 8 feet.

The vertex of the function is at (-1, 24). This means at -1 second, the maximum height is 24 feet. The function is wrong since the time cnnot be negative

C. f(t) = –16(t – 1)² – 24

At time (t) = 0. Therefore:

f(0) = –16(0 – 1)² - 24  = -16 - 24 = -40 feet.

The vertex of the function is at (1, -24). This means at one second, the maximum height is -24 feet. This is not correct

D. f(t) = –16(t + 1)² – 24

At time (t) = 0. Therefore:

f(0) = –16(0 + 1)² + 24  = -16 - 24 = 8 feet.

The vertex of the function is at (-1, -24). This means at -1 second, the maximum height is -24 feet. This is not correct

These are the main data: the T-shirt starts at a height of 8 feet when it leaves the cannon and 1 second later reaches a maximum height of 24 feet

So, f(0) = 8 feet and f(1) = 24 feet

That means, that you can evaluate the functions at t = 0 and t = 1 to see which represents those two points, (0, 8) and (1, 24).

A: f(t) = –16(t – 1)^2 + 24

t = 0 => f(0) = - 16 (0 – 1) ^2 + 24 = -16 + 24 = 8 => This is Ok.

t =1 => f(1) = - 16 (1 – 1)^2 + 24 = 0 + 24 => This is Ok.

B: f(t) = –16(t + 1)^2 + 24

t = 0 => f(0) = -16 (0 + 1)^2 + 24 = - 16 + 24 = 8 => this is Ok

t = 1 => f(1) = -16 (1 + 1)^2 + 24 = -16(4) + 24 = - 64 + 24 = - 40 => Wrong

C: f(t) = –16(t – 1)^2 – 24

t = 0 => f(0) = -16 (0 – 1)^2 - 24 = -16 – 24 = - 40 => Wrong

D: f(t) = –16(t + 1)^2 – 24

t = 0 => f(0) = - 16 (0 + 1)^2 – 24 = -16 – 24 = - 40 => Wrong

With tha we have obtained that the answer is the option A.

Answer:

x = 36, y = 84

Step-by-step explanation:

The sum of the 3 angles in a triangle = 180°

Subtract the sum of the 2 given angles from 180 for x

x = 180 - (96 + 48) = 180 - 144 = 36

The exterior angle of a triangle is equal to the sum of the 2 opposite interior angles.

y is an exterior angle of the triangle, thus

y = 48 + 36 = 84

Answer: 3

Step-by-step explanation:

A/B

30/10 = 3

The greatest of following is 10 liter. Option D. is the correct answer.

To solve this question, first we need to understand the term milliliter and liter.

Milliliter is the CGS unit while liter is the SI unit of volume.

1 ml = 0.001 liter,

For solving, we need to convert all milliliter into liter,

hence, A. 1 ml = 0.001 L

            B. 1 L = 1 L

            C. 10 ml = 10* 0.001

                           = 0.01 L

            D. 10 L = 10 L

            E. 100 ml = 100* 0.001 L

                               = 0.1 L

Therefore, the greatest of the following is 10 L.

To know more about volume and conversions,

https://brainly.com/question/27710307

Answer:

D) 10 liters

1 liter = 1000ml

10 liters = 1000×10

= 10'000ml

Answer:

3.39g

Step-by-step explanation:2.69+0.7=3.39g

The mean of the data in the dot plot is approximately 5.33.

By dividing the sum of the numbers by the total number of numbers, the mean, or average, of the given numbers is determined. Mean is equal to (Sum of all Observations / Total Observations).

We must sum up all the values and divide by the total number of values to determine the mean of the data in the dot plot.

The first step is to count the dots for each value:

3 has 3 dots

4 has 5 dots

5 has 6 dots

6 has 8 dots

7 has 5 dots

8 has 3 dots

Then, multiplying each value by the quantity of dots associated with it, we must total up all the products:

(3 x 3) + (4 x 5) + (5 x 6) + (6 x 8) + (7 x 5) + (8 x 3) = 3 + 20 + 30 + 48 + 35 + 24 = 160

Last but not least, we must divide the entire number of values—i.e., dots—by the sum:

160 ÷ (3 + 5 + 6 + 8 + 5 + 3) = 160 ÷ 30 = 5.33

To know more about mean visit:-

https://brainly.com/question/31101410

#SPJ1

Answer:

Dear user,

Answer to your query is provided below

The building is 60.77 ft tall.

Step-by-step explanation:

Explanation is provided below in the image attached

The upper bound is 1842 and lower bound is 1692. By using these boundaries and t-table, the sample mean is 1767 and sample standard deviation = 133.98.

Here, the two boundaries are 1692 and 1842.

Mean = (1692+1842) /2 = 1767

Here the degree of freedom, df = (n-1) = 25-1 =24

Margin of error = (1842-1692)/2 = 75

Confidence level = 99%

From the t table, value of T with confidence level 99% and df= 24 is 2.80

The equation for margin of error is M = Ts/√n

            M= 75 , T= 2.80, n =25

75 = (2.80 × s) / √25

75 = 2.80s/ 5

s = (75×5)/2.80 = 133.928 = 133.93

So the sample mean is 1767 and the standard deviation is 133.93.

For more details regarding mean and standard deviation, kindly refer

https://brainly.com/question/16287436

#SPJ4

Answer:

c=30

v=10

30+10=40

4*30=120

6*10=60

120+60=180

a) The complex solution to the equation 1+2x = -5i+2 is x = -0.5-1.5i.

b) The complex solutions to the equation x² + 2x + 2 = 0 are x = -1 + i and x = -1 - i.

c) The complex solution to the equation x³ = -2 + 2i is x = 1 + i.

d) The complex solution to the equation x¹ = -i 22 1 is x = -i.

a) To solve the equation 1+2x = -5i+2, we rearrange it to isolate the variable x. Subtracting 2 from both sides gives 2x = -5i, and dividing by 2 yields x = -2.5i. Therefore, the complex solution is x = -0.5-1.5i.

b) For the equation x² + 2x + 2 = 0, we can apply the quadratic formula. Substituting the coefficients into the formula gives x = (-2 ± √(-4(1)(2))) / (2(1)). Simplifying further, we have x = (-2 ± √(-8)) / 2. Since the square root of a negative number is an imaginary number, we can express it as x = (-2 ± 2i√2) / 2. Dividing both the numerator and denominator by 2 gives x = -1 ± i√2. Hence, the complex solutions are x = -1 + i and x = -1 - i.

c) To solve x³ = -2 + 2i, we can start by finding the cube root of both sides. The cube root of -2 + 2i is equal to the cube root of its magnitude times the cube root of the complex number itself. The magnitude of -2 + 2i is √((-2)² + 2²) = √8 = 2√2. The cube root of -2 + 2i can be expressed as 2√2 (cos(θ) + i sin(θ)), where θ is the angle whose tangent is 2/(-2) = -1. Therefore, θ = -π/4. The cube root of -2 + 2i is 2√2 (cos(-π/4) + i sin(-π/4)), which simplifies to 2√2 (-√2/2 - i√2/2). The final solution is x = 2√2 (-√2/2 - i√2/2) = -2 - 2i.

d) The equation x¹ = -i 22 1 is equivalent to x = -i. Therefore, the complex solution is x = -i.

Learn more about complex solutions here:

https://brainly.com/question/29070036

#SPJ11

Answer:

126 blue marbles, 24 white marbles

Step-by-step explanation:

The ratio of blue marbles to white marbles is 21 to 4. From this, we have this equation:

\(21x + 4x = 150\)

\(25x = 150\)

\(x = 6\)

So we have 21 × 6 = 126 blue marbles and 4 × 6 = 24 blue marbles.

126/24 = 21/4

The required length of the curve y = sin(2x) for the limits 0 to 2π is equal to 8.944units.

Length of the curve y = sin(2x) from x = 0 to x = 2π,

Use the arc length formula,

L = \(\int_{0}^{2\pi }\)√(1 + (dy/dx)^2) dx

y = sin(2x)

⇒ dy/dx = 2cos(2x)

Plug this into the arc length formula and simplify,

L =\(\int_{0}^{2\pi }\)√(1 + (2cos(2x))^2) dx

L = \(\int_{0}^{2\pi }\) √(1 + 4cos^2(2x)) dx

This integral cannot be solved exactly,

Use numerical methods to approximate the value of the integral.

Use a numerical integration method such as Simpson's rule or the trapezoidal rule.

Using Simpson's rule with a step size of 0.01,

Length of the curve is approximately 8.944 units.

Therefore, the length of the curve for the given limits is equal to 8.944units.

Learn more about length here

brainly.com/question/2516083

#SPJ4

The given question is incomplete, I answer the question in general according to my knowledge:

What is the length of the curve y = sin2x from x = 0 to x = 2π?

The requried, "a" and "b" are positive numbers, the minimum sum (a + b) is 13.711.

To find the minimum sum of two positive numbers whose product is 47, we can use the concept of the arithmetic mean-geometric mean inequality (AM-GM inequality).

The AM-GM inequality states that for any two positive numbers, the arithmetic mean (average) is always greater than or equal to the geometric mean. Mathematically, it can be expressed as:

AM ≥ GM

For two positive numbers "a" and "b," the arithmetic mean is (a + b) / 2, and the geometric mean is √(ab).

Given that the product of the two numbers is 47 (ab = 47), we want to find the minimum value of their sum (a + b).

Using the AM-GM inequality:

(a + b) / 2 ≥ √(ab)

Substitute ab = 47:

(a + b) / 2 ≥ √47

Now, let's solve for the minimum sum (a + b):

a + b ≥ 2(√47)

a + b ≥ 2 * √(47)
a + b ≥  13.711.        

Since "a" and "b" are positive numbers, the minimum sum (a + b) is 13.711.

Learn more about the minimum sum of numbers here:

https://brainly.com/question/33367738

#SPJ12

The least of the integers in arithmetic mean of n consecutive odd integers is 3.

The formula to calculate average or arithmetic mean of evenly distributed set is -

Average = sum of first and last term/2

Keep the values in formula to find the least integer. Since these are consecutively arranged, the first number will be the least number.

10 = first number + 17/2

First number + 17 = 10×2

Performing multiplication on Right Hand Side

First number + 17 = 20

First number = 20 - 17

Performing subtraction

First number = 3

Hence, the least integer is 3.

Learn more about mean -

https://brainly.com/question/20118982

#SPJ4

Answer:

It'll be 18% to the nearest percent

Step-by-step explanation:

2/5 × 45 = 18

Answer:

The answer is 18%

Step-by-step explanation:

The formula to find experimental probability is number of favorable outcomes/total number of trails. Our favorable outcome here is C ( the outcome we want), and it occurs 8 times. The spinner is spun 45 times so there are 45 trials. This means we get 8/45. 8 divided by 45 equals 0.177777778. When rounded up equals 0.18=18%.

Hope this helps for you K12 math test.

Answer:

-40%

Step-by-step explanation:

NV = new value

OV = old value

percent change = (NV - OV)/(OV) × 100%

percent change = (30 - 50)/(50) × 100%

percent change = -20/50 × 100%

percent change = -40%

Answer:

3rd option

Step-by-step explanation:

The equation of a line in point slope form is

y - b = m(x - a)

where m is the slope and (a, b ) a point on the line

Given

y - 4 = \(\frac{1}{4}\) (x - 8)

with m = \(\frac{1}{4}\) and (a, b) = (8, 4 )

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept ) , then

y = \(\frac{1}{4}\) x + c ← is the partial equation

To find c substitute (8, 4) into the partial equation

4 = 2 + c ⇒ c = 4 - 2 = 2

y = \(\frac{1}{4}\) x + 2 ← equation in slope- intercept form

The given statement that a trinomial is always a higher degree than a monomial is false because greater number of terms does not means higher degree.

A monomial is an algebraic expression with only one term. Or we can say that the representation of a single concept is a monomial.

An example of an unary expression is: 12

A trinomial is an algebraic expression containing three terms. An example of a ternary is: x + y + 7

A trinomial is always of higher degree than a monomial is false statement .

A counterexample can be used to explain why this is wrong. Suppose we have a monomial, 8⁵ and then a trinomial x² + 2x + 3 . This is just a random example. This monomial has a higher degree because 5 is greater than 2. So basically it doesn't matter what the monomial is, if the degree is higher it is just a term than the maximum degree of the trinomial. Just because this has three terms does not mean that the highest degree term is greater than his one term in the monomial.

To learn more about Monomial and trinomial, refer:

https://brainly.com/question/24620388

#SPJ4

The volume of oil exiting the pipe is approximately 100 cu in/hr, 2,400 cu in/day, and 1.39 cu ft/day when converting cu in/day to cubic feet per day.



To calculate the volume of oil exiting the pipe every hour, you would need to know the flow rate of the oil in cubic inches per hour. Let's assume the flow rate is 100 cubic inches per hour.To find the volume of oil exiting the pipe every day, you would multiply the flow rate by the number of hours in a day. There are 24 hours in a day, so the volume of oil exiting the pipe every day would be 100 cubic inches per hour multiplied by 24 hours, which equals 2,400 cubic inches per day.

To convert the volume from cubic inches per day to cubic feet per day, you would need to divide the volume in cubic inches by the number of cubic inches in a cubic foot. There are 1,728 cubic inches in a cubic foot. So, dividing 2,400 cubic inches per day by 1,728 cubic inches per cubic foot, we get approximately 1.39 cubic feet per day.

Therefore, the volume of oil exiting the pipe is approximately 100 cubic inches per hour, 2,400 cubic inches per day, and 1.39 cubic feet per day.

To learn more about volume click here

brainly.com/question/22907480

#SPJ11

Answer:

4+x=5

Step-by-step explanation:

4+x=5

To rotate a point 180° clockwise about the origin, we essentially need to flip the point across the x-axis and then across the y-axis. So the x-coordinate of point A' is -3.

This means that the x-coordinate of the point will become its opposite (negation) and the y-coordinate of the point will also become its opposite.

So, in this problem, we have the point A with coordinates (3, 2). To rotate this point 180° clockwise about the origin, we will negate both the x and y coordinates of the point:

The negation of 3 is -3, so the new x-coordinate of the point will be -3.

The negation of 2 is -2, so the new y-coordinate of the point will be -2.

Putting these together, we get the new coordinate of the point A' as (-3, -2).

So the x-coordinate of point A' is -3.

To learn more about origin please click on below link.

https://brainly.com/question/28528569

#SPJ4