A bakery sells 10 types of pies: apple, cherry, blueberry, strawberry, peach, key lime, pumpkin, sweet potato, pecan, and chocolate. Assume that it has an unlimited supply of each type. How many different ways are there to choose 6 pies from these 10 types if... a. ...there are no restrictions? b. ...all the pies chosen are of the same type? C. ...all the pies chosen are of different types? d. ...at least 2 apple pies and 1 cherry pie are chosen? e....at most 3 key lime pies are chosen?
Answers
The required set of combinations are:
a. 210, b. 10, c. 210, d. 10, e. 481
a. To choose 6 pies from 10 types without any restrictions, we can use the combination formula:
10C6 = 210 ways.
b. To choose 6 pies of the same type, we can simply choose one of the 10 types, so there are 10 ways.
c. To choose 6 pies of different types, we can use the permutation formula:
10P6 = 151,200 ways.
d. To choose at least 2 apple pies and 1 cherry pie, we can split this into two cases:
Case 1: 2 apple pies, 1 cherry pie, and 3 other pies. We can choose the 2 apple pies from the 2 apple pies available, the 1 cherry pie from the 1 cherry pie available, and the 3 other pies from the remaining 8 types. Using the multiplication principle, there are (2C2) x (1C1) x (8C3) = 56 ways to choose the pies in this case.
Case 2: 3 or more apple pies, 1 cherry pie, and 2 other pies. We can choose the 3 or more apple pies from the 2 apple pies available, the 1 cherry pie from the 1 cherry pie available, and the 2 other pies from the remaining 8 types. Using the multiplication principle, there are (2C3 + 2C4 + 2C5 + 2C6) x (1C1) x (8C2) = 700 ways to choose the pies in this case.
Adding the number of ways from both cases, we get a total of 56 + 700 = 756 ways.
e. To choose at most 3 key lime pies, we can split this into three cases:
Case 1: 0 key lime pies. We can choose any 6 pies from the remaining 9 types, so there are 9C6 = 84 ways to choose the pies in this case.
Case 2: 1 key lime pie. We can choose 1 key lime pie from the 3 available, and the remaining 5 pies from the remaining 9 types. Using the multiplication principle, there are (3C1) x (9C5) = 945 ways to choose the pies in this case.
Case 3: 2 or 3 key lime pies. We can choose 2 or 3 key lime pies from the 3 available, and the remaining pies from the remaining 9 types. Using the multiplication principle, there are (3C2 + 3C3) x (9C4 + 9C3) = 10,395 ways to choose the pies in this case.
Adding the number of ways from all three cases, we get a total of 84 + 945 + 10,395 = 11,424 ways.
To know more about combinations,
https://brainly.com/question/20211959
#SPJ11
Related Questions
I need some help please I got to get this done

Answers
Answer:
\(\huge\boxed{\sf 6(x + 2)}\)
Step-by-step explanation:
= 2(5x + 3) - 2(2x - 3)
Expand
= 10x + 6 - 4x + 6
Combine like terms
= 10x - 4x + 6 + 6
Add or subtract as indicated
= 6x + 12
Take 6 common
= 6(x + 2)
\(\rule[225]{225}{2}\)
Hope this helped!
~AH1807If x=8 and y=−3, evaluate the following expression:6x−8y
Answers
Answer:
72
Step-by-step explanation:
here's your solution
=> x= 8
=> y= -3
=> putting the value
=> 8*6 - (8*-3)
=> 48 + 24
=> 72
hope it helps
Hey there!
If x = 8 and y = -3, then SUBSTITUTE it into the equation
6(8) - 8(-3)
6(8) = 48
48 - 8(-3)
8(-3) = -24
48 - (-24)
- & - = +
48 + 24 = 72
Answer: 72
Good luck on your assignment and enjoy your day!
~Amphitrite1040:)
Find the missing side length 12 cm 1,200 cm 20 cm ____ cm

Answers
Answer:
Missing side length is 5 cm.Step-by-step explanation:
Multiply 20 by 12:
20 * 12 = 240.Multiply 240 by 5:
240 * 5 = 1200.Multiply the lengths:
20 * 12= 240 * 5= 1200.Answer:
The missing side is 5 cm
Step-by-step explanation:
Step 1: Determine the missing side
\(V=l*w*h\)
\(1200\ cm^3 = 20\ cm * w * 12\ cm\)
\(\frac{1200\ cm^3}{20\ cm * 12\ cm} = w\)
\(\frac{1200\ cm^3}{240\ cm^2} = w\)
\(5\ cm = w\)
Answer: The missing side is 5 cm
Rebecca is baking three cakes for a big party. If the recipe for one cake calls for 123 cups of flour, how many cups of flour does she need for three cakes?
Answers
The total number of cups of flour that Rebecca will need to bake three cakes is 369 cups of flour.
What is multiplication?Multiplication is the process of multiplying, therefore, adding a number to itself for the number of times stated. For example, 3 × 4 means 3 is added to itself 4 times, and vice versa for the other number.
Given that the recipe for one cake calls for 123 cups of flour. Also, Rebecca needs to bake three cakes, therefore, the total number of cups of flour that Rebecca will need is,
Total number of cups of flour = Number of cakes × Number of cups of flour in a cake
= 3 cakes × 123 cups of flour per cake
= 369 cups of flour
Hence, the total number of cups of flour that Rebecca will need to bake three cakes is 369 cups of flour.
Learn more about Multiplication here:
https://brainly.com/question/14059007
#SPJ1
5. Use the Lagrange multiplier method to find the values of and y which maximise the function f(x,y)=x^1/2y^1/2 subject to the constraint 2x +y = 20. 6. A sequence of numbers xo, 01.12.... is such that so = 1 and, for each n > 1
xn = 1/3xn-1 + 2
Find an explicit expression for , in terms of n. Hence describe the behaviour of xn as n -> infinity.
Answers
Using the Lagrange multiplier method, the maximum values of x and y for the given function and constraint are x = 8 and y = 4.
To maximize the function f(x, y) = x^(1/2) * y^(1/2) subject to the constraint 2x + y = 20, we can employ the Lagrange multiplier method.
Set up the Lagrange function L(x, y, λ) = f(x, y) - λ(g(x, y)), where g(x, y) represents the constraint equation.
Differentiate L with respect to x, y, and λ, and set the partial derivatives equal to zero.
Solve the resulting system of equations to find critical points.
Evaluate the critical points and check the endpoints of the feasible region.
Determine the maximum values of x and y that maximize the function f(x, y) while satisfying the given constraint.
Applying these steps, we find that x = 8 and y = 4 maximize the function f(x, y) subject to the constraint. Thus, the maximum values of x and y are 8 and 4, respectively.
Learn more about Lagrange multiplier method here: brainly.com/question/31133918
#SPJ11
Determine whether each vector can be written as a linear combination of vectors S 1) 8= {(2₁-1₁3), (5,0,4)} a) 2- (-1₁-2.2); c) w = (1₁-8, 12) b) v = (8,-14, 27/4) d) (1,1,-1)
Answers
We are given a set of vectors S and we need to determine whether each given vector can be written as a linear combination of the vectors in S.
(a) For vector (2, -1, -2), we need to check if there exist scalars k₁ and k₂ such that k₁(2, -1, 3) + k₂(5, 0, 4) = (2, -1, -2). By solving the system of equations, we find that k₁ = -1 and k₂ = 0, so the vector can be written as a linear combination of the vectors in S.
(b) For vector (8, -14, 27/4), we need to check if there exist scalars k₁ and k₂ such that k₁(2, -1, 3) + k₂(5, 0, 4) = (8, -14, 27/4). By solving the system of equations, we find that there are no solutions, so the vector cannot be written as a linear combination of the vectors in S.
(c) For vector (1, -8, 12), we need to check if there exist scalars k₁ and k₂ such that k₁(2, -1, 3) + k₂(5, 0, 4) = (1, -8, 12). By solving the system of equations, we find that there are no solutions, so the vector cannot be written as a linear combination of the vectors in S.
(d) For vector (1, 1, -1), we need to check if there exist scalars k₁ and k₂ such that k₁(2, -1, 3) + k₂(5, 0, 4) = (1, 1, -1). By solving the system of equations, we find that there are no solutions, so the vector cannot be written as a linear combination of the vectors in S.
Learn more about vectors here: brainly.com/question/29740341
#SPJ11
I NEED HELP ON THIS ASAP!!! WILL GIVE BRAINLIEST!!

Answers
The best measure of center is the mean
The are 20 students represented by the whisker
The percentage of classrooms with 23 or more is 25%
The percentage of classrooms with 17 to 23 is 50%
The best measure of centerFrom the question, we have the following parameters that can be used in our computation:
The box plot
There are no outlier on the boxplot
This means that the best measure of center is mean
The students in the whiskerHere, we calculate the range
So, we have
Range = 30 - 10
Evaluate
Range = 20
The percentage of classrooms with 23 or moreFrom the boxplot, we have
Third quartile = 23
This means that the percentage of classrooms with 23 or more is 25%
The percentage of classrooms with 17 to 23From the boxplot, we have
First quartile = 15
Third quartile = 23
This means that the percentage of classrooms with 17 to 23 is 50%
Read more about boxplot at
https://brainly.com/question/3473797
#SPJ1
4. John took a new job for a company that offers him an average raise in pay of $3,000 per year. After 5 years on the job, John's annual salary was $58,000. Slope / Rate Y-intercept Ordered pair (point)(x, y)
Part A: Write an equation that John can be used to calculate his annual salary, y, over any given number of years, X.
Part B: How much will John's salary be after working for 10 years? Part C: What does the y-intercept represent in this problem?
part c. what does the Y-intercept represent in this problem

Answers
Answer:
part c is the correct answer to this question
Janelle won 27 tickets at the fair. She traded the tickets for 9 prizes. Each prize was worth the same number of tickets was each prize worth?
Answers
Answer:
3
Step-by-step explanation:
27 tickets = 9 prizes
Since they are all equal, it would be 27 divided by 9 = 3
jasper
Answers
of aviation,
there is no way a bee
should be able to fly.
Its wings are too small to get
its fat little body off the ground.
The bee, of course, flies anyway
because bees don't care
what humans think is impossible.
Yellow, black. Yellow, black.
Yellow, black. Yellow, black.
Ooh, black and yellow!
Let's shake it up a little.
Barry! Breakfast is ready!
Ooming!
Hang on a second.
Hello?
- Barry?
- Adam?
- Oan you believe this is happening?
- I can't. I'll pick you up.
Looking sharp.
Use the stairs. Your father
paid good money for those.
Sorry. I'm excited.
Here's the graduate.
We're very proud of you, son.
A perfect report card, all B's.
Very proud.
Ma! I got a thing going here.
- You got lint on your fuzz.
- Ow! That's me!
- Wave to us! We'll be in row 118,000.
- Bye!
Barry, I told you,
stop flying in the house!
- Hey, Adam.
- Hey, Barry.
- Is that fuzz gel?
- A little. Special day, graduation.
Never thought I'd make it.
Three days grade school,
three days high school.
Those were awkward.
Three days college. I'm glad I took
a day and hitchhiked around the hive.
You did come back different.
- Hi, Barry.
- Artie, growing a mustache? Looks good.
- Hear about Frankie?
- Yeah.
- You going to the funeral?
- No, I'm not going.
Everybody knows,
sting someone, you die.
Don't waste it on a squirrel.
Such a hothead.
I guess he could have
just gotten out of the way.
I love this incorporating
an amusement park into our day.
That's why we don't need vacations.
Boy, quite a bit of pomp...
under the circumstances.
- Well, Adam, today we are men.
- We are!
- Bee-men.
- Amen!
Hallelujah!
Students, faculty, distinguished bees,
please welcome Dean Buzzwell.
Welcome, New Hive Oity
graduating class of...
...9:15.
That concludes our ceremonies.
And begins your career
at Honex Industries!
Will we pick ourjob today?
I heard it's just orientation.
Heads up! Here we go.
Keep your hands and antennas
inside the tram at all times.
- Wonder what it'll be like?
- A little scary.
Welcome to Honex,
a division of Honesco
and a part of the Hexagon Group.
This is it!
Wow.
Wow.
We know that you, as a bee,
have worked your whole life
to get to the point where you
can work for your whole life.
Honey begins when our valiant Pollen
Jocks bring the nectar to the hive.
Our top-secret formula
is automatically color-corrected,
scent-adjusted and bubble-contoured
into this soothing sweet syrup
with its distinctive
golden glow you know as...
Honey!
- That girl was hot.
- She's my cousin!
- She is?
- Yes, we're all cousins.
- Right. You're right.
- At Honex, we constantly strive
to improve every aspect
of bee existence.
These bees are stress-testing
a new helmet technology.
- What do you think he makes?
- Not enough.
Here we have our latest advancement,
the Krelman.
- What does that do?
- Oatches that little strand of honey
that hangs after you pour it.
Saves us millions.
Oan anyone work on the Krelman?
Of course. Most bee jobs are
small ones. But bees know
that every small job,
if it's done well, means a lot.
But choose carefully
because you'll stay in the job
you pick for the rest of your life.
The same job the rest of your life?
I didn't know that.
What's the difference?
You'll be happy to know that bees,
as a species, haven't had one day off
in 27 million years.
So you'll just work us to death?
We'll sure try.
Wow! That blew my mind!
"What's the difference?"
How can you say that?
One job forever?
That's an insane choice to have to make.
I'm relieved. Now we only have
to make one decision in life.
But, Adam, how could they
never have told us that?
Why would you question anything?
We're bees.
We're the most perfectly
functioning society on Earth.
You ever think maybe things
work a little too well here?
Like what? Give me one example.
I don't know. But you know
what I'm talking about.
Please clear the gate.
Royal Nectar Force on approach.
Wait a second. Oheck it out.
- Hey, those are Pollen Jocks!
- Wow.
I've never seen them this close.
They know what it's like
Consider the following list of weights,
x
, of children in (kg).
54.8, 56.4, 69.3, 53.8, 57.7, 47.6, 30.7, 36.9, 44.8, 52.5, 42.1, 57.3, 63.9, 65.3, 49.6, 46.4, 46.3, 49, 46.2, 60.5, 45.2, 43, 66.5, 38.5
Answers

to estimate the percentage of defects in a recent manufacturing batch, a quality control manager at sony selects every 16th music cd that comes off the assembly line starting with the ninth until she obtains a sample of 140 music cds.
Answers
The quality control manager at Sony uses systematic sampling to estimate the percentage of defects in a manufacturing batch of music CDs. Therefore, the quality control manager can estimate that approximately 20% of the entire manufacturing batch of music CDs may have defects based on the systematic sample she obtained.
Systematic sampling involves selecting items from a population at regular intervals. In this case, the quality control manager selects every 16th music CD starting from the ninth. This method ensures that every CD has an equal chance of being selected, providing a representative sample of the batch.
By using systematic sampling, the quality control manager obtains a sample of 140 music CDs. She can then examine these CDs to determine the number of defective ones. Let's assume she finds 28 defective CDs in the sample.
To estimate the percentage of defects in the manufacturing batch, the quality control manager can use the formula:
Defect percentage = (Number of defective CDs / Sample size) *100
Substituting the values, we have \((\frac{28}{140}) * 100 = 20%\).
Therefore, the quality control manager can estimate that approximately 20% of the entire manufacturing batch of music CDs may have defects based on the systematic sample she obtained. This estimation provides valuable information for assessing the quality of the batch and taking necessary actions for improvement.
Learn more about systematic sampling here:
https://brainly.com/question/1550235
#SPJ11
Four people each roll a fair die once. Quantity A: The probability that at least two people will roll the same number Quantity B: 70%
Answers
How likely something is to occur is known as its probability.Probability when die rolled 1st time is 6C1 i.e. (1,2,3,4,5,6).
Find the probability ?How likely something is to occur is known as its probability.We can discuss the probabilities of various outcomes—how likely they are—when we aren't sure how a particular event will turn out. Statistics describes the examination of events subject to probability.
Probability when die rolled 1st time=6C1 i.e. (1,2,3,4,5,6) suppose 1 comes, then 2nd time it should not be .as it is given that no 2 people will roll same number.
so 2nd time probability=5C1 i.e. (2,3,4,5,6). same way 3rd and 4th time probability=4C1 and 3C1 respectively.Probability that no one rolls the same no. = 6*5*4*3and total possibility =6^4
p(same number)= 6*5*4*3/ 6^4
= 5/18
p(no same number will roll)=1-5/18
=13/18
To learn more about probability refer
https://brainly.com/question/25870256
#SPJ4
10.8.7: scheduling meals at a school. a school cook plans her calendar for the month of february in which there are 20 school days. she plans exactly one meal per school day. unfortunately, she only knows how to cook ten different meals. (a) how many ways are there for her to plan her schedule of menus for the 20 school days if there are no restrictions on the number of times she cooks a particular type of meal? (b) how many ways are there for her to plan her schedule of menus if she wants to cook each meal the same number of times?
Answers
The school cook has 10^20 ways to plan her schedule without restrictions, and if she wants to cook each meal the same number of times, she has a specific combination of 20 school days for each meal.
(a) To calculate the number of ways for the school cook to plan her schedule of menus for the 20 school days without any restrictions on the number of times she cooks a particular type of meal, we can use the concept of permutations.
Since she knows how to cook ten different meals, she has ten options for each of the 20 school days. Therefore, the total number of ways she can plan her schedule is calculated by finding the product of the number of options for each day:
Number of ways = 10 * 10 * 10 * ... * 10 (20 times)
= 10^20
Hence, there are 10^20 ways for her to plan her schedule of menus for the 20 school days without any restrictions on the number of times she cooks a particular type of meal.
(b) If the school cook wants to cook each meal the same number of times, she needs to distribute the 20 school days equally among the ten different meals.
To calculate the number of ways for her to plan her schedule under this constraint, we can use the concept of combinations. We need to determine the number of ways to select a certain number of school days for each meal from the total of 20 days.
Since she wants to cook each meal the same number of times, she needs to divide the 20 days equally among the ten meals. This means she will assign two days for each meal.
Using the combination formula, the number of ways to select two school days for each meal from the 20 days is:
Number of ways = C(20, 2) * C(18, 2) * C(16, 2) * ... * C(4, 2)
= (20! / (2!(20-2)!)) * (18! / (2!(18-2)!)) * (16! / (2!(16-2)!)) * ... * (4! / (2!(4-2)!))
Simplifying the expression gives us the final result.
To know more about combination,
https://brainly.com/question/29451244
#SPJ11
1) the owner of a video store has determined that the cost c, in dollars, of operating the store is approximately given by where x is the number of videos rented daily. find the lowest cost to the nearest dollar. a) $400 b) $500 c) $650 d) $550
Answers
The lower cost will occur at the extreme point, that is if the number of videos rented daily is 8 pieces and the cost will be $550.
The cost function is given by:
C(x) = 2x² - 32x + 678
The lowest cost happens at the extreme point. In this point the derivative of C(x) is equal to zero.
Take the derivative:
C'(x) = 4x - 32 = 0
4x = 32
x = 32/4 = 8
Hence, the lowest cost will occur if the number of video rented daily is 8 pcs.
Substitute x = 8 into the cost function:
C(8) = 2(8)² - 32.(8) + 678 = 550
Complete question:
The owner of a video store has determined that the cost c, C(x) = 2x² - 32x + 678 in dollars, of operating the store is approximately given by where x is the number of videos rented daily. find the lowest cost to the nearest dollar
Learn more about cost function here:
https://brainly.com/question/2292799
#SPJ4
Which rule describes the composition of transformations that maps δbcd to δb"c"d"? translation of 5 units x, negative 6 units y composition reflection across y = negative x reflection across y = negative x composition translation of 5 units x, negative 6 units y. translation of 6 units x, negative 5 units y composition reflection across the y-axis reflection across the y-axis composition translation of 6 units x, negative 5 units y
Answers
The rule which describe the composition of transformations that
maps ΔBCD to ΔB"C"D" is:
Reflection across the y-axis composition translation of 6 units x,
negative 5 units y ⇒ last answer
Step-by-step explanation:
Let us revise the reflection across the y-axis , horizontal translation
and vertical translation
1. If point (x , y) is reflected across the y-axis, then its image is (-x , y)
2. If point (x , y) is translated h units to the right, then its image is
(x + h , y), if translated h units to the left, then its image is (x - h , y)
3. If point (x , y) is translated k units up, then its image is (x , y + k),
if translated k units down, then its image is (x , y - k)
∵ The vertices of triangle BCD are (1 , 4) , (1 , 2) , (5 , 3)
∵ The vertices of triangle B'C'D' are (-1 , 4) , (-1 , 2) , (-5 , 3)
∵ The x-coordinates of the vertices of Δ B'C'D' have the same
magnitude of x-coordinates of Δ BCD and opposite signs
∴ Δ B'C'D' is the image of Δ ABC after reflection across the y-axis
∵ The vertices of triangle B'C'D' are (-1 , 4) , (-1 , 2) , (-5 , 3)
∵ The vertices of triangle B''C''D'' are (5 , -1) , (5 , -3) , (1 , -2)
∵ The image of -1 is 5 and the image of -5 is 1
∴ The x-coordinates of the vertices of triangle B'C'D' are added by 6
∵ The image of 4 is -1 , image of 2 is -3 and the image of 3 is -2
∴ The y-coordinates of the vertices of triangle B'C'D' are subtracted
by 5
∴ Δ B"C"D" is the image of Δ B'C'D' by translate 6 units to the right
and 5 units down ⇒ (x + 6 , y - 5)
The rule which describe the composition of transformations that
maps ΔBCD to ΔB"C"D" is:
Reflection across the y-axis composition translation of 6 units x,
negative 5 units y
Learn more about reflection here brainly.com/question/11203617
#SPJ1
The composition of transformations that maps BCD to B"C"D" is described by the following rule:
Composition translation of 6 units x, negative 5 units y across the y-axis last response
Let us rewrite the y-axis reflection, horizontal translation, and vertical translation.
1. If point (x, y) is mirrored across the y-axis, the image of that point is (-x , y)
2. If point (x, y) is translated h units to the right, its image is (x + h, y), and if it is translated h units to the left, its image is (x + h, y) (x - h , y)
3. If point (x, y) is translated k units up, its image is (x, y + k), but if it is translated k units down, its image is (x , y - k)
∵ Triangle BCD has (1, 4) vertices, (1, 2) vertices, and (5, 3) vertices. Triangle B'C'D' has (-1, 4) vertices, (1, 2) vertices, and (5, 3) vertices. The x-coordinates of the B'C'D' vertices have the same magnitude as the x-coordinates of BCD and opposite signs. B'C'D' is the picture of ABC after it has been reflected across the y-axis.
The vertices of triangle B'C'D' are (-1, 4), (-1, 2), (-5, 3), (1, -2)
The vertices of triangle B"C"D" are (5, -1), (5, -3), (1, -2)
The x-coordinates of the triangle B'C'D' vertices are added by 6.
The image of 4 is -1, the image of 2 is -3, and the image of 3 is -2.
The y-coordinates of triangle B'C'D' vertices are subtracted by 5.
∴ Δ B"C"D" is the image of Δ B'C'D' by translating 6 units to the right
and 5 units down ⇒ (x + 6 , y - 5)
The rule which describe the composition of transformations that
maps ΔBCD to ΔB"C"D" is:
Reflection across the y-axis composition translation of 6 units x,
negative 5 units y
Learn more about reflection here:
brainly.com/question/11203617
#SPJ1
a card is drawn from a standard deck and replaced. after the deck is shuffled, another card is pulled. what is the probability that the first card drawn is a heart and the second card is a spade? (enter your probability as a fraction.)
Answers
If a card is drawn from a standard deck and replaced. after the deck is shuffled, another card is pulled. Then the probability that the first card drawn is a heart and the second card is a spade is 1/16.
The probability of drawing a heart on the first card is 1/4 since there are 13 hearts out of a total of 52 cards in a standard deck.
After replacing the card and shuffling the deck, the probability of drawing a spade on the second card is also 1/4 since there are 13 spades out of a total of 52 cards in the deck (assuming the deck is well-shuffled).
To find the probability of both events happening (drawing a heart and then a spade), we multiply the individual probabilities together:
Probability = (1/4) * (1/4) = 1/16
Therefore, the probability that the first card drawn is a heart and the second card is a spade is 1/16.
To learn more about probability: https://brainly.com/question/13604758
#SPJ11
In 2017 the Hindu festival of Diwali occurred on Thursday, 19 October. What fraction of the year was this
Answers
The Diwali occurred on 0.408 or 40.8% of the year in 2017.
To find the fraction of the year that Diwali occurred in 2017, we need to divide the number of days between Diwali and the start of the year by the total number of days in the year.
Diwali occurred on Thursday, October 19, 2017. The start of the year 2017 is January 1, 2017 which is a Sunday.
There are 365 days in a non-leap year. Since 2017 is not a leap year, there are 365 days in that year.
So the fraction of the year that Diwali occurred in 2017 can be calculated as: (days between Diwali and the start of the year) / (total days in the year) = ( 19 + 31 + 30 + 31 + 30 + 19 ) / 365 = (148) / 365 = 0.408
So, the Diwali occurred on 0.408 or 40.8% of the year in 2017.
Therefore, Diwali occurred on 0.408 or 40.8%
To learn more about fractions,
Visit; brainly.com/question/10354322
#SPJ4
The circle shown above has a radius of 4. The central angle, a, of the sector is 2/3n and the arc length represented by b
Determine whether each statement is true about the circle shown above. Select True or False for each statement.
radians, and the arc length is represented
Answers
A circle is a curve sketched out by a point moving in a plane. Except for the first statement both the second and the third statement is true.
What is a circle?A circle is a curve sketched out by a point moving in a plane so that its distance from a given point is constant; alternatively, it is the shape formed by all points in a plane that are at a set distance from a given point, the center.
The complete question is mentioned in the below image.
For the given circle,
The area of the sector is,
Area of sector = π(4)²×[2π/(3×2π)] = 16π/3
The area of the circle is,
Area of the circle = π×(4)² = 16π
The length of the Arc is,
Length of the arc = 2π×(4)×[2π/(3×2π)] = 8π/3
Hence, Except for the first statement both the second and the third statement is true.
Learn more about Circle:
https://brainly.com/question/11833983
#SPJ1

El último informe digital de Perú, publicado en el mes de febrero, reveló que hay 19,9 millones de internautas. Asimismo, hay 27 millones de usuarios activos en los medios sociales En la siguiente gráfica se presentan datos por rango de edad y género en porcentajes.
Si se desea realizar una encuesta a usuarios peruanos de las diversas redes sociales en el 2021, ¿cuál es la probabilidad de que el primer usuario que responda la encuesta sea mujer de más de 44 años?

Answers
Desde el gráfico, se encuentra que hay una probabilidad de 9.9% que el primer usuario que responda la encuesta sea mujer de más de 44 años.
------------------------
El gráfico muestra el porcentaje de usuarios de redes sociales correspondiente a características de género y edad.De el gráfico, hay:
Una probabilidad de 5.1% que el primer usuario sea mujer entre 45 y 54 años.2.7% que sea mujer entre 55 y 64 años.2.1% que sea mujer con más de 65 años.5.1% + 2.7% + 2.1% = 9.9%, puesto que:
Hay una probabilidad de 9.9% que el primer usuario que responda la encuesta sea mujer de más de 44 años.
Un problema similar es dado en https://brainly.com/question/18734831
what is the purpose of the permutation test? group of answer choices for hypothesis testing of mean, median, and quartiles, it is used to synthesize the population distribution of the statistic of interest for hypothesis testing of mean, median, and quartiles, it is used to synthesize the sampling distribution under the null
Answers
Permutation test is used to synthesize the population distribution of the statistic of interest for hypothesis testing of mean, median, and quartiles
An estimation of the population distribution—the distribution from which our observations originated—is the goal of a permutation test. We can then calculate how uncommon our observed values are in comparison to the population.
I find the permutation test to be more natural, and it only relies on the assumption of random assignment of treatment groups.
In a permutation test, you compare the observed test statistic to the distribution of values
you get when the treatment group assignments are shuffled/randomized/permuted.
The null hypothesis that two distinct groups originate from the same distribution is tested using permutation tests, also known as exact tests, randomization tests, or re-randomization tests. A permutation test can be used for hypothesis testing or significance testing (including A/B testing) without requiring any presumptions to be made about the distribution of the samples, such as that the samples must be normally distributed.
To know more about permutation here
https://brainly.com/question/14632937
#SPJ4
Whats the square root of 10000
Answers
Answer: 100
Step-by-step explanation:
Answer:
The square root of 10000 is 100
Step-by-step explanation:
In a state lottery, 25 balls are numbered from 1-25 are placed in a machine. Then 6 numbers are randomly drawn. What is the probability that a player that buys one ticket will win $10,000?
Answers
The probability that you win a prize is 0.00003797372
Here, we have,
From the question, we have the following parameters:
Sample Space = 1 to 22
This means that
Sample size, n = 22 i.e. the count of numbers from 1 to 22
The count of numbers to be drawn is 5
So, the individual probabilities are
P(1) = 5/22
P(2) = 4/21
P(3) = 3/20
P(4) = 2/19
P(5) = 1/18
The probability of winning is the product of the above
So, we have
p = 5/22 * 4/21 * 3/20 * 2/19 * 1/18
Evaluate
p = 0.00003797372
Hence, the probability is 0.00003797372
Read more about probability at
brainly.com/question/24756209
#SPJ1
complete question:
In a certain state's lottery, 22 balls numbered 1 through 22 are placed in a machine and 5 of them are drawn at random. If the 5 numbers drawn match the numbers that a player had chosen, the player wins $30,000. In this lottery, THE ORDER THE NUMBERS ARE DRAWN DOES MATTER. Compute the probability that you win the prize if you purchase a single lottery ticket.
consider circle c below, where the central angle is measured in radians. circle c is shown. line segments r c and s c are radii. angle r c s is startfraction 5 pi over 6 endfraction. arc r s has a measure of 10 pi. what is the length of the radius? units
Answers
Answer:
The answer is 12 units
Step-by-step explanation:
The length of the radius is 12 units
What is radius?The radius of a circle is a line drawn from the center of the circle to its circumference
The length (L) of the arc is given as:
\(L = 10\pi\)
The length of an arc is:
\(L = r\theta\)
So, we have:
\(r\theta =10\pi\)
The angle at the center of the circle is \(\frac{5\pi}{6}\)
So, we have:
\(r* \frac{5\pi}{6}=10\pi\)
Multiply both sides by 6
\(r* 5\pi=60\pi\)
Divide both sides by 5pi
\(r = 12\)
Hence, the length of the radius is 12 units
Read more about radius at:
https://brainly.com/question/6613758
3. The mass m is less than 5 kilograms.
Answers
Answer:
5 minus m ( variable)
Step-by-step explanation:
np
What error did Leah make?

Answers
Answer:
the lines arent parallel, so you cant use corresponding angles theorem
The error is corresponding property does not apply.
What are parallel lines?Parallel lines are those lines that are equidistant from each other and never meet, no matter how much they may be extended in either directions. For example, the opposite sides of a rectangle represent parallel lines.
We know that when two lines are parallel they the following property:
Alternate interior angleCorresponding angleco- interior angles.As, there is no parallel lines line.
So, the measurement if <1 = 88 can't be true because corresponding doesn't apply.
Learn ore about parallel lines here:
https://brainly.com/question/12860077
#SPJ2
the ""4p"" model of resisting corruption focuses on becoming aware of it
Answers
The 4P model of resisting corruption is a useful framework that can be utilized to combat corruption. It emphasizes the importance of prevention, punishment, promotion, and participation.
The 4P model is a method of combating corruption by focusing on becoming more aware of it. It is a framework that includes four elements:
Prevention, Punishment, Promotion, and Participation.
The first component of the 4P model is prevention, which entails identifying and eliminating the underlying causes of corruption. The objective is to minimize the opportunities for corruption and to promote ethical behavior.
This can be achieved through the establishment of strong policies and regulations, as well as the implementation of accountability mechanisms.
The second element of the 4P model is punishment. When corruption occurs, penalizing those who engage in it is critical to deter others from doing so. This entails implementing strict laws and regulations and ensuring that those caught face harsh consequences.
The third component of the 4P model is promotion. This element is all about promoting transparency and ethical conduct. The aim is to create a culture of integrity where people are encouraged to do the right thing and transparency is prioritized.
The 4P model of resisting corruption is a useful framework that can be utilized to combat corruption. It emphasizes the importance of prevention, punishment, promotion, and participation.
To know more about the 4P model, visit:
brainly.com/question/32704108
#SPJ11
Which of the following represents the relationship between the circumference, c, and diameter, d, of any circle?

Answers
Given:
Circumference of a circle = C
Diameter of a circle = d
To find:
The relationship between the circumference, c, and diameter, d, of any circle.
Solution:
We know that, circumference of a circle is
\(C=2\pi r\)
It can be written as
\(C=(2r)\pi \)
\(C=d\pi \) \([\because d=2r]\)
On dividing both sides by d, we get
\(\dfrac{C}{d}=\pi \)
Therefore, the correct option is (F).
Is (-2,-4) a solution of the graphed inequality?
Choose 1 answer:
Yes
No
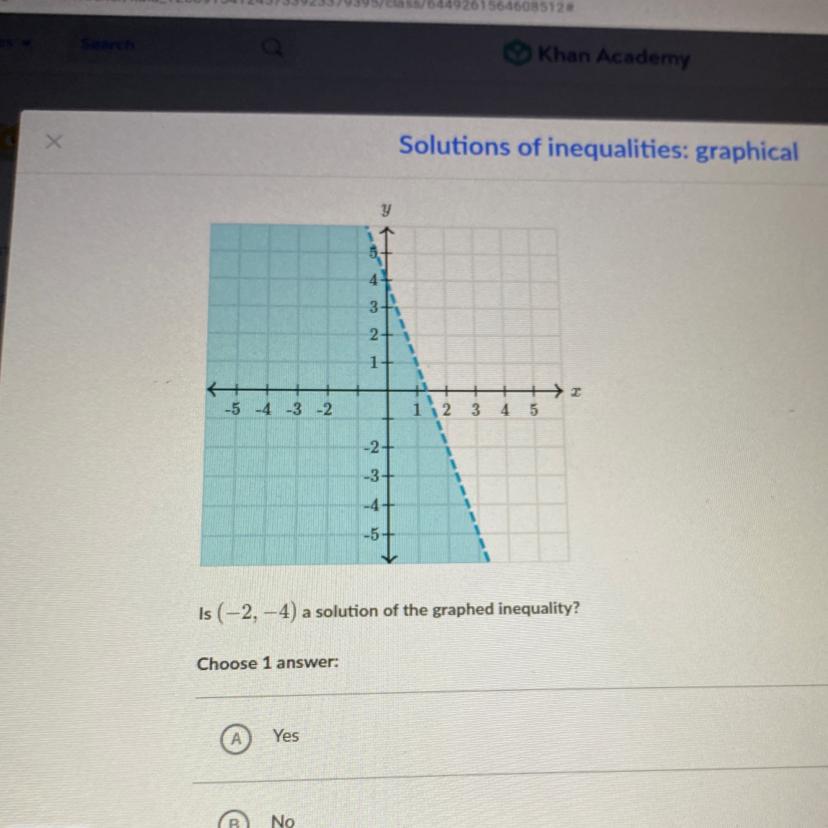
Answers
Answer:
Yes
General Formulas and Concepts:
Algebra I
Reading a coordinate graphCoordinates (x, y)Solving inequalitiesStep-by-step explanation:
When we plot (-2, -4) onto the graph, we can envision that the point is within the shaded region of the graphed line.
∴ (-2, -4) would be a solution.
Do not include anything other than numbers in your responses. For example, do not include comma or dollar sign in your numbers. As a rule of thumb, keep 2 decimal places for larger numbers and 3 decimal places for smaller numbers less than 1. An accounts department is concerned about the number of internal purchase forms that its users completed incorrectly. As a result they are monitoring the proportion of purchase forms that were not completed correctly. This was chosen, rather than measuring the actual number of defects, because any number of defects on a form required about the same effort to revise. The following table shows number of forms completed incorrectly "out of 200 forms" that is processed each day. Construct a control chart for the data that monitors the proportion of incorrect forms. Is the process in control? Day 1 2 Number of Incorrect Forms 13 13 3 15 4 13 19 5 6 13 15 7 8 16 9 13 10 13 Sum 143 IMPORTANT: In this problem, keep 3 decimal places in your calculations. Which of the following charts is appropriate? (P Chart/C Chart) Based on your choice on the last question, calculate "one" of the followings, P (for P chart), or C (for C chart): If you chose P Chart, how much is standard deviation of p (sigma_p)? (Write 0 if you are not doing P chart) Upper Control Limit: Lower Control Limit: Is the proportion of incorrect forms in control? (Yes/No)
Answers
We can determine if the process is in control by checking if any of the data points fall outside the control limits.
To construct a control chart for monitoring the proportion of incorrect forms, we will use the P chart because we are interested in monitoring the proportion of defects relative to the total number of forms processed.
To calculate the standard deviation of p (sigma_p) for the P chart, we can use the formula:
sigma_p = sqrt((p * (1 - p)) / n)
where:
p = average proportion of defective forms
n = number of forms processed
First, let's calculate the average proportion of defective forms (p):
p = Sum of incorrect forms / (200 * Number of days)
p = 143 / (200 * 10)
p ≈ 0.0715
Next, let's calculate sigma_p using the formula mentioned above:
sigma_p = sqrt((0.0715 * (1 - 0.0715)) / (200 * 10))
sigma_p ≈ 0.0093
For the P chart, the Upper Control Limit (UCL) is given by:
UCL = p + 3 * sigma_p
UCL ≈ 0.0715 + 3 * 0.0093
UCL ≈ 0.0994
The Lower Control Limit (LCL) for the P chart is typically set to zero since the proportion cannot be negative:
LCL = 0
Now, we can determine if the process is in control by checking if any of the data points fall outside the control limits.
Learn more about data from
https://brainly.com/question/30459199
#SPJ11