A data set had values ranging from 117 to 139. A new data point of 30 was
added to the data set. Would this point affect the mean or the median more? How
(increase/decrease) and why? (2 points)
Answers
Answer:
This point would affect the mean more because the median is less sensitive to outliers.
Step-by-step explanation:
Hope this helps!
Related Questions
Solve for x
2x + 10 = -3x - 15
A -5
B -7
C -4
D -2
Answers
Answer:
A. x = -5
2(-5) + 10 = -3(-5) - 15
0 = 0
Find two 2 possible value of the geometric mean of 16 and 36
Answers
Answer:
\(\pm24\)
Step-by-step explanation:
To find the geometric mean of two numbers, you find their product and then take the square root of that product:
\(GM=\sqrt{16*36}=\sqrt{576}=\pm24\)
Please explain your answer to the question in the picture with steps.

Answers

help please quickly and give explanation

Answers
Answer:
Because y is a common variable, we can assume that they are equal to each other.

A cabin on a ferris wheel has traveled one fourth of the circumference
of the wheel, a distance of 117.75 feet. What is the radius, in feet, of
the ferris wheel? Use 3.14 for pi
Answers
Solving for the circumference and using the formula for the circumference we got the radius as 74.95 feet
Mensuration of Flat ShapesGiven Data
1/4 of the circumference = 117.75 feet.
Let the circumference be x feet
1/4*x = 117.75
x/4 = 117.75
cross multiplying
x = 4*117.75
x = 471 feets
The expression for the circumference is given as
C = 2πr
471 = 2πr
Making r subject of formula we have
r = = 471/2*3.142
r = 471/6.284
r = 74.95 feet
Learn more about Circles here
https://brainly.com/question/24375372
Among the cast aluminum parts manufactured on a certain day, 90% were flawless, 8% had only a minor flaw, and 2% had major flaws. Suppose we select a random part from the production line. What is the probability that the part has at least one flaw
Answers
Answer:
10% probability that the part has at least one flaw
Step-by-step explanation:
We have these following probabilities:
90% probability of the part being flawless.
8% probability of the part having a minor flaw
2% probability of the part having major flaws.
What is the probability that the part has at least one flaw
Minor or major flaws. So 8% + 2% = 10%
10% probability that the part has at least one flaw
PLEASE HELP ASAP
Use trigonometry to resolve the following vectors into components. Describe the vectors
using vector notation.

Answers
step by step explanation:
Calc II Question
Find the volume of the solid obtained by rotating the region bonded bt the given curves about the specified line.
Y = e^-x
Y = 1
X = 2
About the Y = 2
Answers
Answer:
\(\displaystyle \frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Step-by-step explanation:
This can be solved with either the washer (easier) or the shell method (harder). For the disk/washer method, the slice is perpendicular to the axis of revolution, whereas, for the shell method, the slice is parallel to the axis of revolution. I'll show how to do it with both:
Shell Method (Horizontal Axis)
\(\displaystyle V=2\pi\int^d_cr(y)h(y)\,dy\)
Radius: \(r(y)=2-y\) (distance from y=2 to x-axis)
Height: \(h(y)=2-(-\ln y)=2+\ln y\) (\(y=e^{-x}\) is the same as \(x=-\ln y\))
Bounds: \([c,d]=[e^{-2},1]\) (plugging x-bounds in gets you this)
Plugging in our integral, we get:
\(\displaystyle V=2\pi\int^1_{e^{-2}}(2-y)(2+\ln y)\,dy=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Washer Method (Parallel to x-axis)
\(\displaystyle V=\pi\int^b_a\biggr(R(x)^2-r(x)^2\biggr)\,dx\)
Outer Radius: \(R(x)=2-e^{-x}\) (distance between \(y=2\) and \(y=e^{-x}\))
Inner Radius: \(r(x)=2-1=1\) (distance between \(y=2\) and \(y=1\))
Bounds: \([a,b]=[0,2]\)
Plugging in our integral, we get:
\(\displaystyle V=\pi\int^2_0\biggr((2-e^{-x})^2-1^2\biggr)\,dx\\\\V=\pi\int^2_0\biggr((4-4e^{-x}+e^{-2x})-1\biggr)\,dx\\\\V=\pi\int^2_0(3-4e^{-x}+e^{-2x})\,dx\\\\V=\pi\biggr(3x+4e^{-x}-\frac{1}{2}e^{-2x}\biggr)\biggr|^2_0\\\\V=\pi\biggr[\biggr(3(2)+4e^{-2}-\frac{1}{2}e^{-2(2)}\biggr)-\biggr(3(0)+4e^{-0}-\frac{1}{2}e^{-2(0)}\biggr)\biggr]\\\\V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\biggr(4-\frac{1}{2}\biggr)\biggr]\)
\(\displaystyle V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\frac{7}{2}\biggr]\\\\V=\pi\biggr(\frac{5}{2}+4e^{-2}-\frac{1}{2}e^{-4}\biggr)\\\\V=\pi\biggr(\frac{5}{2}+\frac{4}{e^2}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4}{2e^4}+\frac{8e^2}{2e^4}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4+8e^2-1}{2e^4}\biggr)\\\\V=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Use your best judgment when deciding on what method you use when visualizing the solid, but I hope this helped!

A manufacturer of chocolate chips would like to know whether its bag filling machine works correctly at the 442 gram setting. It is believed that the machine is underfilling the bags. A 44 bag sample had a mean of 438 grams. Assume the population variance is known to be 576. A level of significance of 0.1 will be used. Find the P-value of the test statistic. You may write the P-value as a range using interval notation, or as a decimal value rounded to four decimal places.
Answers
Answer:
p value is 0.1343
Step-by-step explanation:
Null: u>= 442
Alternative: u < 442
Using the formula for z score:
(x - u)/sd/√n
Where x is 438, u = 442 sd can be determined from the variance = √variance =√576 = 24 and n = 44
z score = 438-442 / (24/√44)
z score = -4/(24/6.6332)
z = -4/3.6182
z =-1.1055
Now let's find the p value at 0.1 significance level using a z score of -1.1055, using a p value calculator, p value is 0.1343 which greatest than 0.1 meaning the day is not sufficient enough to conclude that the machine is underfilling the bags.
The population of Boca Raton can be predicted using the function p(n)=74,760+1940n, where n is the number of years since 2000. In what year will the predicted population of Boca Raton reach 100,000?
Answers
In 2014, the predicted population of Boca Raton will be 100000.
Given that the population function of Boca Raton is,
p(n) = 74760+1940n
So when the population of Boca Raton is 100000, then
p(n) = 100000
So,
100000 = 74760+1940n
1940n = 100000-74760
1940n = 25240
n = 25240/1940 = 14 (approximately)
So, the year in which the predicted population of Boca Raton reach 100000 is = 2000+14 = 2014
To know more about Population Function refer to:
https://brainly.com/question/25896797
#SPJ1
Suppose the function h(x) = 2x - 9 is translated up 5 units to become a new function,
Xx). What's the equation of the new function?
A) x) = 7x-4
B)(x) = 2x - 14
C)(x) = 7x-9
D) (x)=2x-4
Answers
According to the given data the equation of the new function is (D) f(x) = 2x - 4.
What is meant by equation?An equation is a mathematical statement that indicates that two expressions are equal. It contains an equals sign "=" and may involve variables, constants, and mathematical operations such as addition, subtraction, multiplication, division, exponentiation, etc.
According to the given information:If we translate the function h(x) = 2x - 9 up by 5 units, the new function f(x) will have the form:
f(x) = h(x) + 5
Substituting the definition of h(x) into this equation, we get:
f(x) = 2x - 9 + 5
Simplifying, we have:
f(x) = 2x - 4
Therefore, the equation of the new function is (D) f(x) = 2x - 4.
To know more about equations visit:-
https://brainly.com/question/22964920
#SPJ1
I need help please!!!

Answers
Siama and Wills used different methods to find the differences between (5x + 6x) and (2x - 1) but they both arrived at the same answer.
I prefer Wills method because it is easier and less complicated.
How to solve differences?Wills method:
(5x + 6x) - (2x - 1)
Subtract both 2x and -1
5x + 6x - 2x - - 1
5x + 4x + 1
In conclusion, Wills method is preferred when both methods are compared.
Read more on difference of numbers:
https://brainly.com/question/17301989
#SPJ1
What is -20/2(7 2/3)
Answers
The simplified form of -20/2(7 2/3) is -230/3.
To solve the expression -20/2(7 2/3), we need to follow the order of operations, which states that we should perform the operations inside parentheses first, then any multiplication or division from left to right, and finally any addition or subtraction from left to right.
First, let's convert the mixed number 7 2/3 to an improper fraction.
7 2/3 = (7 * 3 + 2) / 3 = 23/3
Now, let's substitute the value back into the expression:
-20/2 * (23/3)
Next, we simplify the multiplication:
-10 * (23/3)
To multiply a fraction by a whole number, we multiply the numerator by the whole number:
-10 * 23 / 3
Now, we perform the multiplication:
-230 / 3
Therefore, the simplified form of -20/2(7 2/3) is -230/3.
for such more question on simplified form
https://brainly.com/question/11680269
#SPJ8
A plane flies with a speed of 600 mph. What distance will it fly
in 3 /5 hours,11/12 hours, 4/15 hours?
Answers
Answer:
3/5=360 mph 11/12=550 4/15=160
Step-by-step explanation:
Given a loan amount P, an annual interest rate r, and the length of the loan in years, find the monthly payment R necessary to pay off the loan by completing parts a through c. Represent the number of monthly payments by n.
Answers
Answer: To find the monthly payment R necessary to pay off a loan, we can use the following formula:
R = P * (r/12) / (1 - (1 + r/12)^(-12n))
where P is the loan amount, r is the annual interest rate (as a decimal), and n is the number of years of the loan.
To complete parts a through c, we'll need to make some assumptions about the loan. Let's assume:
P = $10,000
r = 5% (0.05 as a decimal)
n = 3 years
a) Calculate the number of monthly payments.
Since the loan is for 3 years, the number of monthly payments will be:
n = 3 * 12 = 36
So there will be 36 monthly payments.
b) Calculate the monthly payment.
Substituting the given values into the formula, we get:
R = 10000 * (0.05/12) / (1 - (1 + 0.05/12)^(-12*3))
R = $299.71 (rounded to the nearest cent)
So the monthly payment necessary to pay off the loan is $299.71.
c) Verify that the loan is paid off in 3 years.
To verify that the loan is paid off in 3 years, we can multiply the number of monthly payments by the monthly payment amount:
36 * $299.71 = $10,789.56
Since the original loan amount was $10,000, and the total paid over 36 months is $10,789.56, the loan is paid off in 3 years (with a bit extra paid due to the interest).
Step-by-step explanation:
Find the standard form of the equation of the line through (8,-3) that is parallel to the line 3y=4x+8
Answers
The standard form of the equation of the line passing through (8,-3) that is parallel to the line 3y=4x+8 is 4x - 3y = 41
How to represent equation in standard form?The equation of the line in standard form can be represented as follows:
Ax + By = C
where
A, B and C are constantTherefore, the standard form of the equation of the line through (8,-3) that is parallel to the line 3y = 4x + 8 is a s follows;
Parallel lines have the same slope.
Hence,
3y = 4x + 8
y = 4 / 3 x + 8 / 3
The slope of the line is 4 / 3. Hence, the line passes through (8, -3). let's find the y-intercept.
y = 4 / 3 x + b
-3 = 4 / 3 (8) + b
b = -3 - 32 / 3
b = -9 - 32/ 3
b = -41 / 3
Hence,
y = 4 / 3 x - 41 / 3
multiply through by 3
3y = 4x - 41
Therefore, the standard form is 4x - 3y = 41
learn more on standard form here: https://brainly.com/question/11479371
#SPJ1
What values of x
and y
satisfy the system of equations {8x+9y=−36 x+7y=1}
Enter your answer as an ordered pair, like this: (42, 53)
If your answer includes one or more fractions, use the / symbol to separate numerators and denominators. For example, if your answer is (4253,6475),
enter it like this: (42/53, 64/75)
If there is no solution, enter "no"; if there are infinitely many solutions, enter "inf."
Answers
The solution to the system of equations is (x, y) = (-261/47, 44/47) as an ordered pair.
To solve the given system of equations:
Equation 1: 8x + 9y = -36
Equation 2: x + 7y = 1
We can use the method of substitution or elimination to find the values of x and y. Let's use the method of substitution:
From Equation 2, we can solve for x:
x = 1 - 7y
Substituting this value of x into Equation 1:
8(1 - 7y) + 9y = -36
8 - 56y + 9y = -36
-47y = -44
y = 44/47
Substituting the value of y back into Equation 2 to find x:
x + 7(44/47) = 1
x + 308/47 = 1
x = 1 - 308/47
x = (47 - 308)/47
x = -261/47
Therefore, as an ordered pair, the solution to the system of equations is (x, y) = (-261/47, 44/47).
Learn more about system of equation on:
https://brainly.com/question/12526075
Call: Im(formula = Repair.Costs ~ Miles.Driven, data = Dataset) Residuals: Min 1Q Median 3Q Max -247.81 -144.68 29.07 64.89 343.86 Coefficients: Estimate (Intercept) 72.807562 Miles.Driven 0.009792 Std. Error 89.456108 0.001601 t value 0.814 6.117 Pr>It) 0.432 5.2e-05 *** Signif. codes: 0) ****' 0.001 '**'0.01 '*' 0.05'.'0.1''1 Residual standard error: 180.3 on 12 degrees of freedom Multiple R-squared: 0.7572, Adjusted R-squared: 0.7369 F-statistic: 37.42 on 1 and 12 DF, p-value: 5.2e-05
Using these regression results, what is the estimated repair cost on a car that has 74,000 miles on it?
Answers
Answer:
797.42
Step-by-step explanation:
Given the Output of a linear regression data using R;
From the result table;
Intercept = 72.807562
Gradient or slope = 0.009792
General form of a linear equation:
y = mx + c
Where y = response variable ; x = explanatory variable ; c = intercept and m = gradient / slope
Hence, the regression equation becomes :
y = 0.009792x + 72.807562
Using these regression results, what is the estimated repair cost on a car that has 74,000 miles on it?
x = 74,000
y = 0.009792(74000) + 72.807562
y = 724.608 + 72.807562
y = 797.42
Answer:
The estimated repair cost on a car that has 74,000 miles on it is $797.42.
Step-by-step explanation:
The statement: Im(formula = Repair.Costs ~ Miles.Driven, data = Dataset) implies that the variable "Repair.Costs" is the dependent variable and the variable "Miles.Driven" is the independent variable.
From the provided data the regression equation formed is:
\(\text{Repair.Costs}=72.807562+0.009792\cdot \text{Miles.Driven}\)
Compute the estimated repair cost on a car that has 74,000 miles on it as follows:
\(\text{Repair.Costs}=72.807562+0.009792\cdot \text{Miles.Driven}\)
\(=72.807562+0.009792\cdot 74000\\\\=72.807562+724.608\\\\=797.415562\\\\\approx 797.42\)
Thus, the estimated repair cost on a car that has 74,000 miles on it is $797.42.
Construct the 99% confidence interval estimate of the mean wake time for a population with the treatment
m
(Round to one decimal place as needed)
ample Get more help-
HW Score: 39.53%, 17 of 43 points
O Points: 0 of 6
A clinical trial was conducted to test the effectiveness of a drug for treating insomnia in older subjects. Before treatment, 14 subjects had a mean wake time of 105 0 min After treatment, the 14 subjects had a
mean wake time of 782 min and a standard deviation of 24 1 min Assume that the 14 sample values appear to be from a normally distributed population and construct a 99% confidence interval estimate of the
mean wake time for a population with drug treatments What does the result suggest about the mean wake time of 105 0 min before the treatment? Does the drug appear to be effective?
Answers
The result suggests that the mean wake time might have really reduced since the values barely fall above 100 min as in before treatment with a high degree of confidence. thus , the drug is effective.
Confidence interval is written in the form as;
(Sample mean - margin of error, sample mean + margin of error)
The sample mean represent x , it is the point estimate for the population mean.
Margin of error = z × s/√n
Where s = sample standard deviation = 21.8
n = number of samples = 17
Now the population standard deviation is unknown and the sample size is small, hence, we would use the t distribution to find the z score
then the degree of freedom, df for the sample.
df = n - 1 = 17 - 1 = 16
Since confidence level = 99% = 0.99, α = 1 - CL = 1 – 0.99 = 0.01
α/2 = 0.01/2 = 0.005
Therefore the area to the right of z0.005 is 0.005 and the area to the left of z0.005 is 1 - 0.005 = 0.995
the t distribution table, z = 2.921
Margin of error = 2.921 × 21.8/√17
= 15.44
The confidence interval for the mean wake time for a population with drug treatments will be; 90.3 ± 15.44
The upper limit is 90.3 + 15.44 = 105.74 mins
The lower limit is 90.3 - 15.44 = 74.86 mins
Learn more about confidence interval here:
https://brainly.com/question/16148560
#SPJ1
Ax^2+bx+c=2(x-1)(2x+3)+(x^2-4x+2)
Answers
The quadratic form ax² + bx + c for the given set of factors is 5x² - 2x - 4.
How do we determine the quadratic equation (ax^2+bx+c) from a given set of factors?The quadratic equation that takes the form ax^2+bx+c can be determined from a given set of factors by applying the rule:
a + (b + c) = a + b + cLet us expand the eqaution: 2(x-1) (2x+3)
Ax^2+bx+c = 2(x-1) (2x+3) + x^2-4x+2So, we have:
2(x - 1)(2x + 3) ⇒ 4x² + 2x - 6.
= 4x² + 2x - 6 + x² - 4x + 2
Now, let us group like terms, we have:
= 4x² + x² + 2x - 4x - 6 + 2
= 5x² - 2x - 4
Therefore, we can conclude that the quadratic form ax² + bx + c for the given set of factors is 5x² - 2x - 4.
Learn more about quadratic equations here:
https://brainly.com/question/25841119
#SPJ1
please help asap!!!!!

Answers
Answer:
Step-by-step explanation:
R= 2,1 Q= 3,3 P= 1,4
If point (4, 5) is on the graph of a function, which equation must be true?
Answers
4 ≤ h(x) ≤5
Answer:
C. f(4)=5
Step-by-step explanation:
I got it right on EDG.
In the figure below,S is between Q and T and R is the midpoint of QS. If RT=9 And RS=4 find QT

Answers
Answer:
QT = 13
Step-by-step explanation:
since R is the midpoint of QS, QR = RS = 4
QT = RT + QR = 9 + 4 = 13
PLS HELP WILL GIVE BRAINLIEST ANSWER

Answers
Answer:
8
Step-by-step explanation:
2(20-8x)=5x-2
40-16x=5x-2
42=21x
x=2
HK=5x-2 = 5(2)-2 = 10-2 = 8
Seth is using the figure shown below to prove Pythagorean Theorem using triangle similarity:
In the given triangle ABC, angle A is 90° and segment AD is perpendicular to segment BC.
The figure shows triangle ABC with right angle at A and segment AD. Point D is on side BC.
Which of these could be a step to prove that BC2 = AB2 + AC2?
possible answers -
By the cross product property, AB2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by AD.
By the cross product property, AB2 = BC multiplied by AD.

Answers
The correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
To prove that \(BC^2 = AB^2 + AC^2\), we can use the triangle similarity and the Pythagorean theorem. Here's a step-by-step explanation:
Given triangle ABC with right angle at A and segment AD perpendicular to segment BC.
By triangle similarity, triangle ABD is similar to triangle ABC. This is because angle A is common, and angle BDA is a right angle (as AD is perpendicular to BC).
Using the proportionality of similar triangles, we can write the following ratio:
\($\frac{AB}{BC} = \frac{AD}{AB}$\)
Cross-multiplying, we get:
\($AB^2 = BC \cdot AD$\)
Similarly, using triangle similarity, triangle ACD is also similar to triangle ABC. This gives us:
\($\frac{AC}{BC} = \frac{AD}{AC}$\)
Cross-multiplying, we have:
\($AC^2 = BC \cdot AD$\)
Now, we can substitute the derived expressions into the original equation:
\($BC^2 = AB^2 + AC^2$\\$BC^2 = (BC \cdot AD) + (BC \cdot AD)$\\$BC^2 = 2 \cdot BC \cdot AD$\)
It was made possible by cross-product property.
Therefore, the correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
For more questions on cross-product property:
https://brainly.com/question/14542172
#SPJ8
A box contains orange balls and green The number of more four the number of orange If there 38 balls how many green balls and how balls are there in the box ?
Answers
let number of green balls= x
let number of orange balls=x+4
x+x+4=38
2x=38-4
2x=34
x=17
number of green balls=17
number of orange balls=21
Find the area of the given circle.
99.8 km

Answers
Answer:
Area = 7822.61542 km²
Step-by-step explanation:
Área of a circle is:
area = π (d/2)²
π = 3.1416
d = diameter
In this case:
area = 3.1416 * (99.8/2)²
area = 3.1416 * 49.9²
area = 3.1416 * 2490.01
area = 7822.61542km²
Anyone know the answer to this question
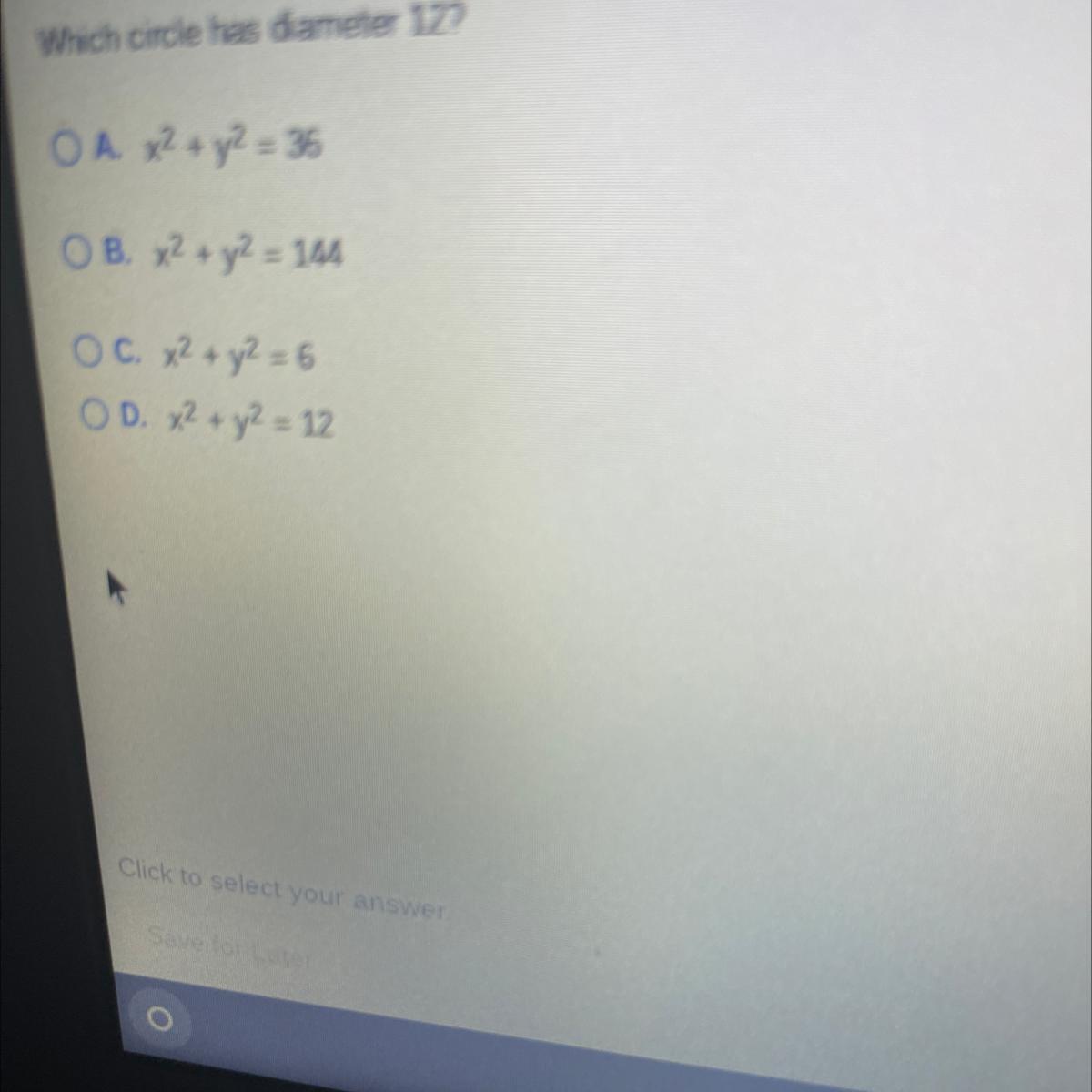
Answers
Answer:
The answer is D.............
Which is an example of Identity Property of Zero?
Answers
Answer:
Identity Property of Zero
The identity property of 0 states that if you add or subtract 0 from any number, the number will always stay the same. Here are some examples involving whole numbers: 3+0=3 7−0=7 Therefore, x+0=0+x=x. This is also known as the additive identity property of 0.
Step-by-step explanation:
Hope it helps :)
A set of data is described as:
The data is around 12. If another measurement were taken, it would probably be around 12.
Which group of measures would lead to this conclusion?
Range—7
Mode—11
Median—12
Mean—12
Range—6
Mode—11
Median—11
Mean—11
Range—14
Mode—12
Median—9
Mean—12
Range—5
Mode—11
Median—12
Mean—10
Answers
The group of measures which would lead to the provided conclusion is the range is 7, the mean of the data is 12, the median is 12 and the mode is 11.
Given that, the data is around 12. If another measurement were taken, it would probably be around 12.
We need to find which group of measures would lead to this conclusion.
What are the mean, median and mode of the data set?The mean of the data is the average value of the given data. The mean of the data is the ratio of the sum of all the values of data to the total number of values of data.
The median of the data is the middle value of the data set when it arrange in ascending or descending order. The data is around 12 which suggests that the median is 12.
Median=12
The mode of a data set is the value, which occurs most times for that data set. The value which has the highest frequency in the given set of data is known as the mode of that data set.
Mean and mode is around the median. For this case, the mean of the data is 12 and the mode is 11.
Mode=11
Mean=12
Thus, the group of measures which would lead to the provided conclusion is the range is 7, the mean of the data is 12, the median is 12 and the mode is 11.
Learn more about the mean, median and mode here;
brainly.com/question/14532771
#SPJ1