A goat is tired to a pole at the center of a square of length of side 20m. If the rope is 10m long. Calculate the (I) area of the square that can't be grazed by the goat (ii) fraction of grazed portion to the whole area
Answers
Answer:
percentage = 78.54%
Step-by-step explanation:
The area of a square of side length x is:
\(A_s=x^2\)
The area of a circle of radius r is:
\(A_c=\pi r^2\)
The goat is tied to a pole at the center of a square of a side length of x=20 cm.
The area of the square is:
\(A_s=20^2\)
\(A_s=400~m^2\)
The rope is 10 m long. The goat is able to graze an area of:
\(A_c=\pi 10^2\)
\(A_c=100\pi~m^2\)
(i)
Since the diameter of the circle (20 m) is equal to the length of the square, the area of the circle is contained in the square and the area of the square not grazed by the goat is:
\(A = A_s-A_c=400~m^2-100\pi~m^2\)
\(A=100(4-\pi)~m^2\)
Calculating:
\(A = 85.84~m^2\)
(ii)
The percentage can be calculated as:
\(\displaystyle \frac{A_c}{A_s}*100=\frac{100\pi}{400}*100=25\pi\)
Calculating:
percentage = 78.54%
Related Questions
The area of a trapezoid is 96 m. If the two bases measure 11m and 13m, solve for the height.
Answers
Answer:
Step-by-step explanation:
Formula
Area = 1/2 (b1 + b2)*h
Givens
b1 = 11 m
b2 = 13 m
Area = 96
h = ?
Solution
96 = 1/2 (11 + 13) * h Multiply by 2 Combine the bases as well.
96*2 = (24) * h Divide by 24
96*2/24 = h Multiply by 2 and divide by 24
h = 8
Select the two equations that will help you to solve this problem:
The combined average weight of an okapi and a llama is 450 kilograms.
3 llamas, on average, weigh 190 kilograms more than an average okapi.
You want to find the average weight of each type of animal.
Answers
Answer:
An average Ilama weighs 160 kilograms and an average okapi weighs 290 kilograms.
Step-by-step explanation:
Let,
x be the average weight of a Ilamas
y be the average weight of an okapi
According to given statement;
x + y = 450 Eqn 1
3x = y + 190 Eqn 2
From Eqn 2
y = 3x - 190 Eqn 3
Putting this value of y in Eqn 1
x + (3x-190) = 450
x + 3x - 190 = 450
4x = 450 + 190
4x = 640
Dividing both sides by 4
\(\frac{4x}{4}=\frac{640}{4}\\x=160\\\)
Putting x = 160 in Eqn 3
y = 3(160) - 190
y = 480 - 190
y = 290
Hence,
An average Ilama weighs 160 kilograms and an average okapi weighs 290 kilograms.
At a high school, the probability that a student is a senior is 0.25. The
probability that a student plays a sport is 0.20. The probability that a student
is a senior and plays a sport is 0.08.
What is the probability that a randomly selected student plays a sport, given
that the student is a senior?
O A. 0.32
• B. 0.08
O C. 0.17
O D. 0.25
Answers
The probability that a randomly selected student plays a sport, given
that the student is a senior is A. 0.32
What is probability?Probability is the chance of occurrence of a certain event out of the total no. of events that can occur in a given context.
This is a case of conditional probability and we know,
Conditional probability is a term used in probability theory to describe the likelihood that one event will follow another given the occurrence of another event.
Given, At a high school, the probability that a student is a senior is 0.25
and the probability that a student is a senior and plays a sport is 0.08.
Therefore, The probability that a randomly selected student plays a sport, given that the student is a senior is,
= 0.08/0.25.
= 0.32
learn more about probability here :
https://brainly.com/question/743546
#SPJ9
i need help with math

Answers
The relationship between the distance that birds fly in relation to the time they do so, is positive.
There are about 3 outliers but for the most part, the relationship is positive.
How to describe the relationship ?The graph which shows the distance that birds fly in relation to the time they do, shows that there is a positive relationship because as the time increases, the distance that the birds have flown also increases.
There are some outliers such as the bird that flew 1 mile in 7 hours but in general, as the time increases, the distance increases as well. There are two clusters of distance as well.
Find out more on relationship at https://brainly.com/question/1599922
#SPJ1
Part A: Choose one value for a and one value for b that would make both of the following inequalities true:
a < b and |b| < |a|
Answers
The correct answer is, by choosing a = -2 and b = 1, we satisfy both inequalities .a < b:
To make both inequalities true, we need to select values for a and b that satisfy the given conditions:
a < b: This inequality means that the value of a should be less than the value of b.
|b| < |a|: This inequality means that the absolute value of b should be less than the absolute value of a.
One possible solution that satisfies both conditions is:
a = -2
b = 1
With these values, we have:
-2 < 1 (a < b)
|-1| < |2| (|b| < |a|)
Therefore, by choosing a = -2 and b = 1, we satisfy both inequalities.a < b:
This inequality states that the value of a should be less than the value of b. In other words, a needs to be positioned to the left of b on the number line. To satisfy this condition, we can choose a to be any number that is less than b. In the example I provided, a = -2 and b = 1, we can see that -2 is indeed less than 1, fulfilling the requirement.
|b| < |a|:
This inequality involves the absolute values of a and b. The absolute value of a number is its distance from zero on the number line, always resulting in a non-negative value. The inequality states that the absolute value of b should be less than the absolute value of a. To satisfy this condition, we can choose b to be any number with a smaller absolute value than a. In the example I provided, |1| is less than |(-2)|, as 1 is closer to zero than -2, fulfilling the requirement.
By selecting a = -2 and b = 1, we satisfy both inequalities: a < b and |b| < |a|. The specific values of -2 and 1 were chosen as an example, but there are multiple other values that would also satisfy the given conditions. The important aspect is that a is indeed less than b, and the absolute value of b is smaller than the absolute value of a.
Learn more about inequality here:
https://brainly.com/question/30238989
#SPJ8
Someone HELPPppp for tmr

Answers
Answer:
y=1x-6
Step-by-step explanation:
First we find the slope by using rise over run. So you can either count up and over(rise/run) or use the slope formula y2-y1/x2-x1. You will find that the slope is 1, so plug that into the equation for mx. So we have y=1x so far. Then we find the y-intercept by looking where the graph intersects the y-axis. As you can see it intersects at -6, so plug -6 into the equation for b. No we have our full equation of y=1x-6.
-Hope this helped
Which is the equation of the circle that has a diameter with endpoints located at (0, –3) and (6, 5)?
(x – 6)^2 + (y – 5)^2 = 100
(x – 3)^2 + (y – 1)^2 = 25
x^2 + (y + 3)^2 = 100
(x – 5)^2 + y^2 = 25
Answers
The equation of the circle that has a diameter with endpoints located at (0, –3) and (6, 5) is;
(x – 3)² + (y – 1)² = 25The midpoint of the diameter of a circle is it's center.
As such; the coordinates of its center are;
x = (0 + 6)x = 3y = (-3 + 5)/2y = 1The coordinates of the center are then; (3, 1)
The radius of a circle is half the length of the diameter;
Radius, r = d/2where; d = √(6-0)² + (5-(-3))²d = √36 + 64d = √100d = 10Therefore, radius, r = 10/2 = 5.
Therefore, the equation of the circle usually takes the form;
(x -f)² + (x -g)² = r²In this scenario; the equation is;
(x – 3)² + (y – 1)² = 25.Read more;;
https://brainly.com/question/16646649
8. Write a paragraph proof.
Proof Given: In a plane, a is perpendicular to b, b id perpendicular to c, and c || d.
Prove: a || d
Answers
To prove that line segment a is parallel to line segment d, based on the given information, we can utilize the properties of perpendicular and parallel lines.
Given that a is perpendicular to b and b is perpendicular to c, we know that angles formed between a and b, as well as between b and c, are right angles. Let's denote these angles as ∠1 and ∠2, respectively.
Now, since c is parallel to d, we can conclude that the corresponding angles ∠2 and ∠3, formed between c and d, are congruent.Considering the fact that ∠2 is a right angle, it can be inferred that ∠3 is also a right angle.
By transitivity, if ∠1 is a right angle and ∠3 is a right angle, then ∠1 and ∠3 are congruent.Since corresponding angles are congruent, and ∠1 and ∠3 are congruent, we can deduce that line segment a is parallel to line segment d.
Thus, we have successfully proven that a is parallel to d based on the given information and the properties of perpendicular and parallel lines.
For more such questions on line segment
https://brainly.com/question/30756145
#SPJ8
16. Find m<2.
a. 86°
b. 43°
C. 94°
d. 133

Answers
Answer : 86 degrees
Type the correct answer in each box. Use numerals instead of words.
Consider this system of linear equations.
4x - 3y = -8
3x + 2y = -6
The solution to this system is ( , )
Answers
To solve the system of linear equations, we can use the method of substitution or elimination. Here, we will use the method of substitution.
From the second equation, we can solve for y in terms of x:
3x + 2y = -6
2y = -3x - 6
y = (-3/2)x - 3
Now we can substitute this expression for y into the first equation:
4x - 3y = -8
4x - 3((-3/2)x - 3) = -8
Simplifying and solving for x, we get:
4x + (9/2)x = 1
(17/2)x = 1
x = -2/17
Now we can substitute this value of x into the expression we found for y:
y = (-3/2)x - 3
y = (-3/2)(-2/17) - 3
y = 1/17 - 3
y = -50/17
Therefore, the solution to the system is (-2, 1).
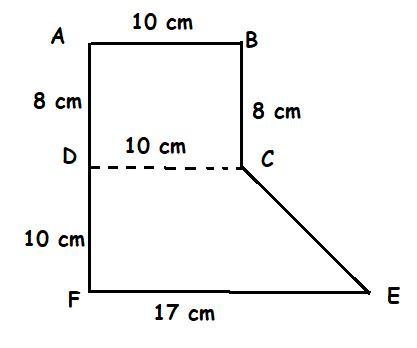
help me pls due in 5 mins

Answers
Answer: \(215\ cm^2\)
Step-by-step explanation:
Given
Here the given figure can be divided into two shapes i.e. rectangle and a trapezium
For rectangle ABCD Area = \(10\times8=80\ cm^2\)
Area of trapezium CEFD Area is \(\frac{1}{2}[\text{sum of non-parallel sides}]\times[\text{distance between them}]\)
\(\Rightarrow \frac{1}{2}\times [10+17][10]=135\ cm^2\)
Total shaded area \(=80+135=215\ cm^2\)
On a coordinate plane, a dashed straight line has a positive slope and goes through (negative 3, 1) and (0, 3). Everything to the left of the line is shaded.
Which linear inequality is represented by the graph?
On a coordinate plane, a dashed straight line has a positive slope and goes through (negative 3, 1) and (0, 3). Everything to the left of the line is shaded.
Which linear inequality is represented by the graph?
Answers
Answer:
2x-3y<-9
Step-by-step explanation:

rectangle has area 80 square centimeters. the rectangle is dilated using A as a center and a scale factor of 1/2 what is the area of the image
Answers
9514 1404 393
Answer:
20 square centimeters
Step-by-step explanation:
The area of the dilated figure is the original area multiplied by the square of the dilation factor. The center of dilation is irrelevant.
dilated area = (1/2)² × original area
dilated area = 1/4 × 80 cm²
dilated area = 20 cm²
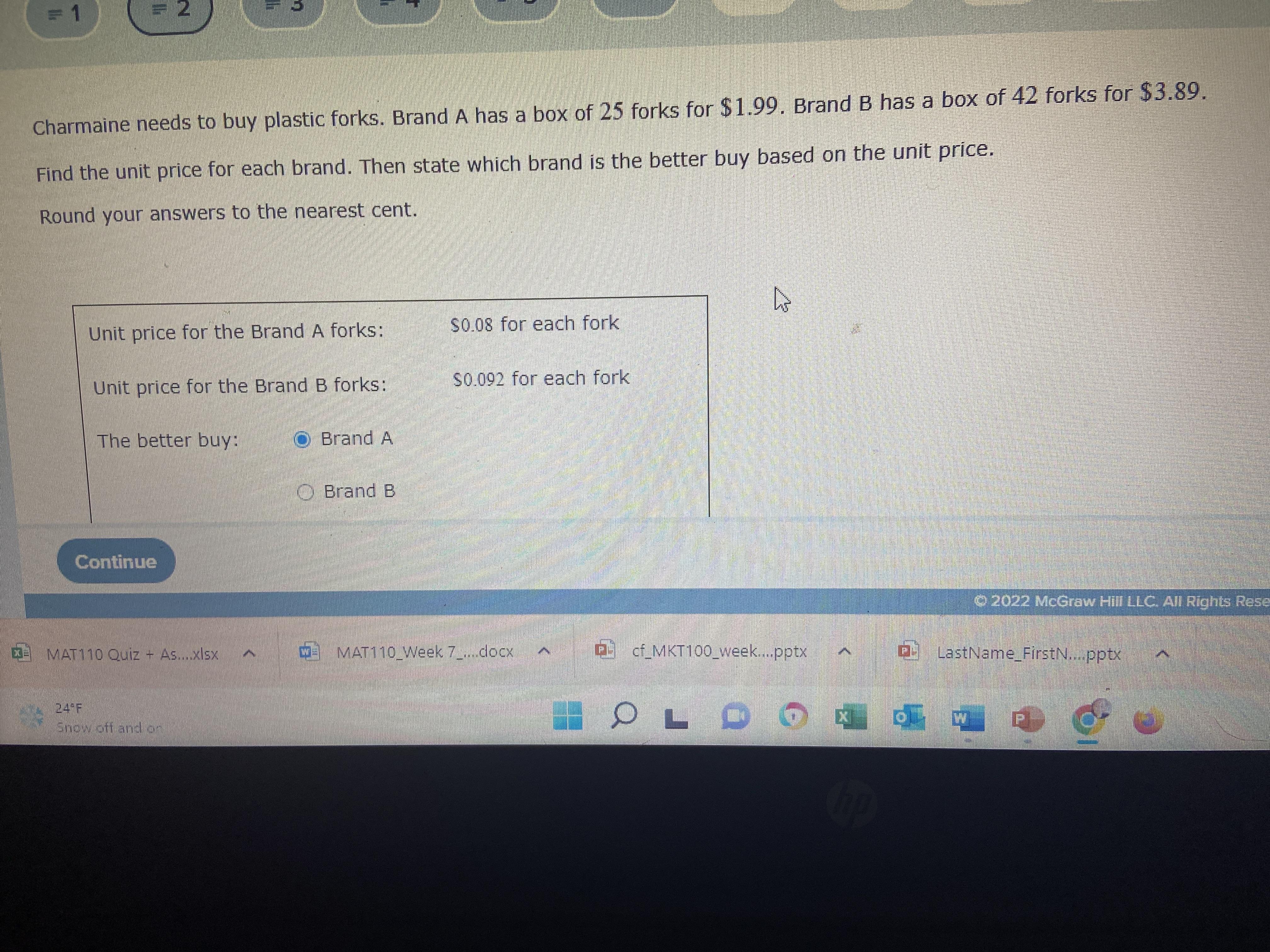
Brand A has a box of 25 forks for 1.99 and Brand B has a box of 42 totals for 3.89. What is the unit price for each brand and what brand is a better buy based on unit price
Answers
Answer:
Brand A
Step-by-step explanation:
Brand A has a box of 25 forks for 1.99
Take the price per fork
1.99 /25 = .0796
.08 per fork
Brand B has a box of 42 totals for 3.89
3.89 / 42
.092319048
.09 per fork
Find the maximum value of s = xy + yz + xz where x+y+z=9.
Answers
From the constraint, we have
\(x+y+z=9 \implies z = 9-x-y\)
so that \(s\) depends only on \(x,y\).
\(s = g(x,y) = xy + y(9-x-y) + x(9-x-y) = 9y - y^2 + 9x - x^2 - xy\)
Find the critical points of \(g\).
\(\dfrac{\partial g}{\partial x} = 9 - 2x - y = 0 \implies 2x + y = 9\)
\(\dfrac{\partial g}{\partial y} = 9 - 2y - x = 0\)
Using the given constraint again, we have the condition
\(x+y+z = 2x+y \implies x=z\)
so that
\(x = 9 - x - y \implies y = 9 - 2x\)
and \(s\) depends only on \(x\).
\(s = h(x) = 9(9-2x) - (9-2x)^2 + 9x - x^2 - x(9-2x) = 18x - 3x^2\)
Find the critical points of \(h\).
\(\dfrac{dh}{dx} = 18 - 6x = 0 \implies x=3\)
It follows that \(y = 9-2\cdot3 = 3\) and \(z=3\), so the only critical point of \(s\) is at (3, 3, 3).
Differentiate \(h\) again and check the sign of the second derivative at the critical point.
\(\dfrac{d^2h}{dx^2} = -6 < 0\)
for all \(x\), which indicates a maximum.
We find that
\(\max\left\{xy+yz+xz \mid x+y+z=9\right\} = \boxed{27} \text{ at } (x,y,z) = (3,3,3)\)
The second derivative at the critical point exists
\($\frac{d^{2} h}{d x^{2}}=-6 < 0\) for all x, which suggests a maximum.
How to find the maximum value?Given, the constraint, we have
x + y + z = 9
⇒ z = 9 - x - y
Let s depend only on x, y.
s = g(x, y)
= xy + y(9 - x - y) + x(9 - x - y)
= 9y - y² + 9x - x² - xy
To estimate the critical points of g.
\($&\frac{\partial g}{\partial x}\) = 9 - 2x - y = 0
\($&\frac{\partial g}{\partial y}\) = 9 - 2y - x = 0
Utilizing the given constraint again,
x + y + z = 2x + y
⇒ x = z
x = 9 - x - y
⇒ y = 9 - 2x, and s depends only on x.
s = h(x) = 9(9 - 2x) - (9 - 2x)² + 9x - x² - x(9 - 2x) = 18x - 3x²
To estimate the critical points of h.
\($\frac{d h}{d x}=18-6 x=0\)
⇒ x = 3
It pursues that y = 9 - 2 \(*\) 3 = 3 and z = 3, so the only critical point of s exists at (3, 3, 3).
Differentiate h again and review the sign of the second derivative at the critical point.
\($\frac{d^{2} h}{d x^{2}}=-6 < 0\)
for all x, which suggests a maximum.
To learn more about constraint refer to:
https://brainly.com/question/24279865
#SPJ9
A stockbroker bought 55 shares of stock for $44.31 each.
Answers
Answer:
whats the question?
Step-by-step explanation:
Answer:
2,437.05
Step-by-step explanation:
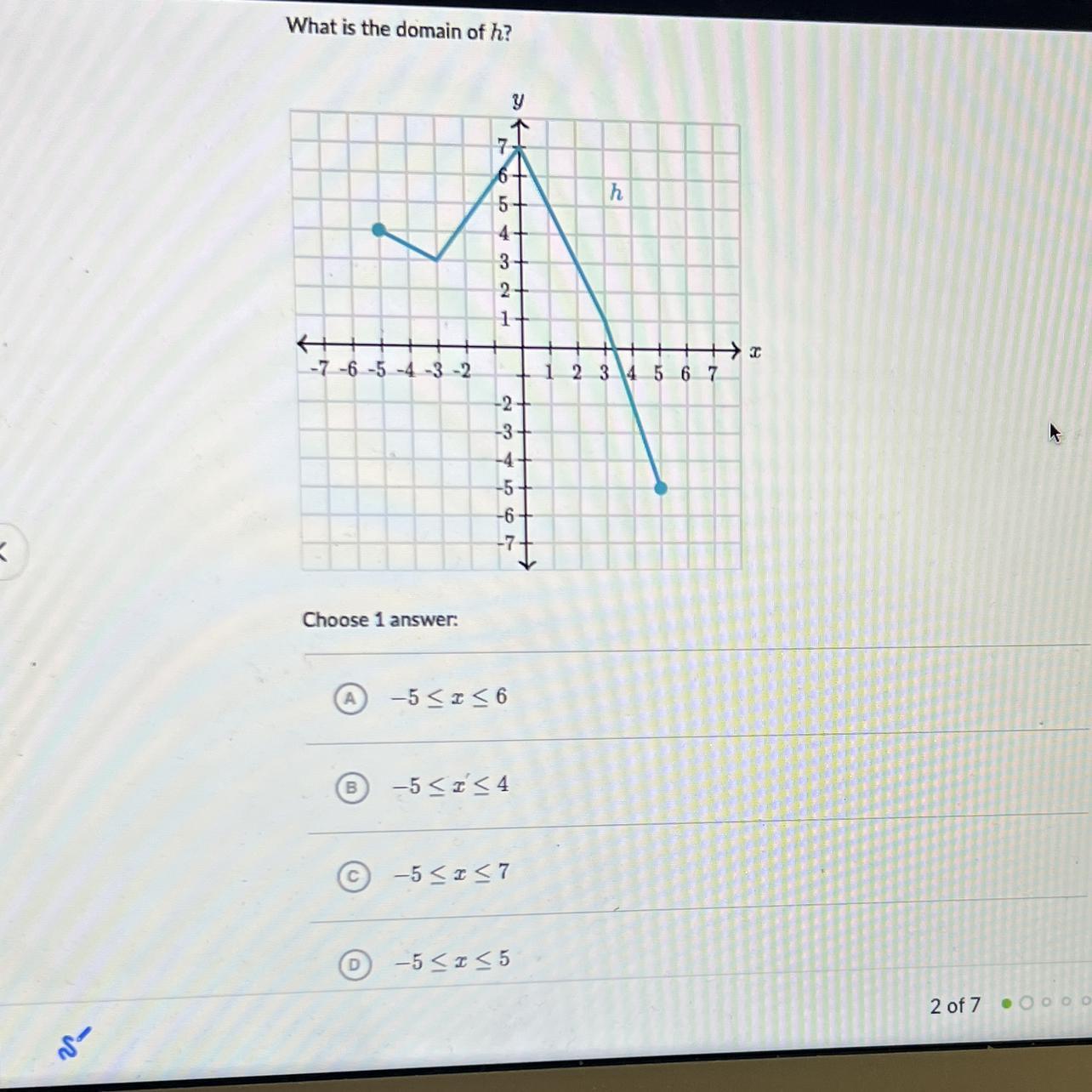
what is the domain of h
Answers
h: The domain
-5 ≤ x ≤ 5
A.right triangle
B.isosceles triangle
C.obtuse triangle
D.scalene triangle
HELP PLSSS THIS IS DUE BY 2:00 AM I NEED IT ASAPPP

Answers
Answer:
B. Isosceles triangleStep-by-step explanation:
It is a vertical section and the figure formed from the cross-section is:
Isosceles triangleCorrect choice is B
What is the vertical displacement of the basic graph to produce a graph of
OA Sunits down
B. 2 units down
OC units down
OD
units up
SUBMIT

Answers
The vertical displacement is of 2 units down, the correct option is B.
What is the vertical displacement?Remember that for a function f(x), a vertical displacement of N units is written in general form as:
g(x) = f(x) + N
If N > 0, the translation is upwards.
if N < 0, the translation is downwards.
Here we assume that we start with the parent cosine function:
y = cos(x)
And the transformed function is:
y = -2 - cos(x - π)
So we have some transformations, but the vertical translation is of 2 units down. So the correct option is B.
Learn more about translations at:
https://brainly.com/question/24850937
#SPJ1
what do you think 40×40 is
And tell how you got your answer
Answers
Answer:
1600
please see the attached picture for full solution
Hope it helps...

2.1. Provide a general rule to describe the relationship between the dates of spread and number of people infected infected.
Answers
The relationship between the dates of spread and the number of people infected can vary depending on various factors such as the infectiousness of the disease, the effectiveness of containment measures, population density, and individual behaviors.
However, there is a general rule that can describe the relationship:As the dates of spread progress, the number of infected individuals tends to increase initially, reaching a peak, and then gradually decreasing over time.
This pattern is often referred to as the epidemic curve or the epidemiological curve. In the early stages of an outbreak, the number of cases may grow rapidly as the disease spreads through a susceptible population. This rapid increase is often influenced by factors such as the contagiousness of the disease, population density, and social interactions.
As containment measures, such as vaccination campaigns, public health interventions, and behavioral changes, are implemented, the rate of new infections may start to decline. This can lead to a peak in the number of cases, after which the curve gradually decreases as the disease is brought under control and fewer susceptible individuals remain.
It's important to note that the specific shape, duration, and magnitude of the epidemic curve can vary significantly depending on the disease and the effectiveness of the response measures implemented. Additionally, emerging variants, changes in behavior, and other factors can impact the trajectory of the epidemic curve.
Know more about disease here:
https://brainly.com/question/27441596
#SPJ11
You have several numbers in a data set: 5, 7, 9, 11, 13, 15, 17. What is the z Score for the number 15? (the SD is 4.32)
Answers
The value of the z-score for the number 15 in a data set is 0.93.
Define z-score.
A data point's z-score, also known as a standard score, indicates how far it deviates from the mean. In practical terms, however, it's a measurement of how many standard deviations a raw number is from or above the population mean.
You can plot a z-score on a normal distribution graph. Z-scores can be anywhere between -3 and +3 standard deviations.
∴ z = (x – μ) / σ
Given:
σ = 4.32
x = 15
Data set: 5, 7, 9, 11, 13, 15, 17
So, mean = 5 + 7 + 9 + 11 + 13 + 15 + 17/7
= 77/7
μ = 11
z = (x – μ) / σ
= (15 - 11)/4.32
= 4/4.32
z = 0.93
To know more about z-score visit:
brainly.com/question/15016913
#SPJ1
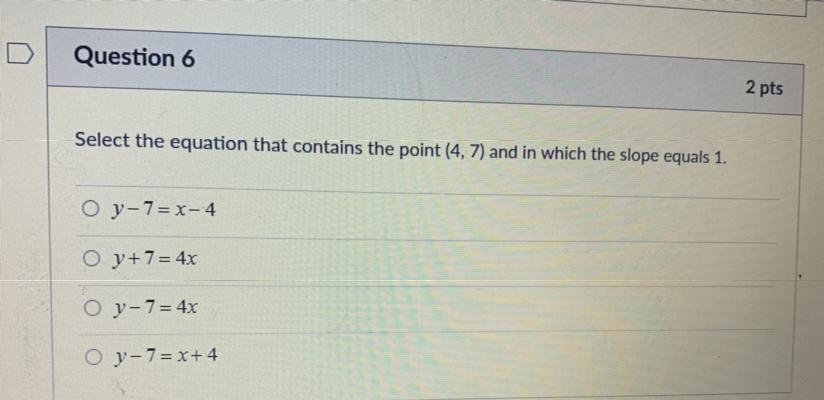
Help me out plssszzszzszz
Answers
Answer:
\(the \: answer \: is \: \\ y - 7 = 1(x - 4) \\ y - 7 = x - 4 \\ or \: in \: other \: way \: \\ y = x+ 3\)
Graph the line with slope -3 passing through the point (1,-5)
Answers
The equation of the line in the standard form exists 3x - y = 2.
What is the equation of a line?The equation of a line is a representation of a line on an x-y plane that illustrates the relationship between x and y for each point on the specific line. When x and y are variables and a, b, and c are constants, a line has the standard form ax + by = c.
Y = mx + b is the slope-intercept form of a line, where x and y are variables, m is the line's slope, and b is the line's y-intercept.
The one-point formula reads: y - y₁ = m(x - x₁). to describe the equation of a line traveling through the point (x1, y1) and having a slope of m.
We are asked to graph a line with a slope = -3, passing through the point (1, -5).
We use the one-point formula to determine the equation of this line, with slope m = -3, (x₁, y₁) = (1, -5).
Substituting these values in the equation y - y₁ = m(x - x₁), we get
Let the equation be y - -5 = -3(x - 1)
simplifying the equation, we get
y = -3x + 3 - 5
y = -3x - 2
3x - y = 2
The equation of the line in the slope-intercept form exists y = -3x - 2
The equation of the line in the standard form exists 3x - y = 2.
We draw the locations (1,-5) (because it is obvious that the line goes through this location) and (0, 2) (since the y-intercept is at 2 and the line passes through the point (0, 2)) in order to graph this line. We draw a line connecting these places, then we expand it on both sides to create the necessary line.
To learn more about standard form refer to:
brainly.com/question/187506
#SPJ1

I NEED HELP PLEASE, THANKSSS! :)

Answers
Answer: A) max at (14, 6) = 64, min at (0,0) = 0
Step-by-step explanation:
Graph the lines at look for the points of intersection.
Input those points into the Constraint function (2x + 6y) and look for the maximum value and minimum value.
Points of Intersection: (0, 0), (17, 0), (0, 10), (14, 6)
Point Constraint 2x + 6y
(0, 0): 2(0) + 6(0) = 0 Minimum
(17, 0): 2(17) + 6(0) = 34
(0, 10): 2(0) + 6(10) = 60
(14, 6): 2(14) + 6(6) = 64 Maximum

Mrs. Grayson uses 2/ 3 of a dozen eggs to make a small chiffon cake. If she wants to bake 6 small chiffon cakes, how many dozen eggs does she need?
Answers
Answer:
Step-by-step explanation:
For one cake= 2/3 dozen
for 6 cakes= 2/3x6=4 dozen
8*6= 48 eggs. 48/12= 4 dozen.
So he needs 4 dozen (48 total eggs) eggs to make 6 small chiffon cakes.
A students score is at the 16th percentile. This indicates that:
A. 16% of scores are at his/her score or below
B. 84% of scores are at his/her score or below.
Answers
Answer:
A. 16% of scores are at his/her score or below
Step-by-step explanation:
When a student's score is at the 16th percentile, it means that their score is equal to or better than 16% of the scores in the population. In other words, 16% of the scores are at their score or below.
One employee of a computer store is paid a base salary of $1000 a month plus an 8% commission on all sales over $7000 during the month. How much must the employee sell in one month to earn a total of $3000 for the month? Write an equation required to find the solution, using x to represent the amount of sales, in dollars, by the employee. nothing
Answers
Answer:
$32,000
Step-by-step explanation:
From the information given, the equation would indicate that the total salary is equal to the base salary plus the result of subtracting $7,000 from the amount of sales for 8%:
1,000+(x-7,000)*0.08=3,000, where x is the amount of sales
Now, you can solve for x:
1,000+0.08x-560=3,000
0.08x+440=3,000
0.08x=3,000-440
x=2,560/0.08
x=32,000
According to this, the answer is that the employee must sell $32,000 in one month to earn a total of $3,000 for the month.
(Stock Level). A.S. Ltd. produces a product 'RED' using two components X and Y. Each unit of 'RED' requires 0.4 kg. of X and 0.6 kg. of Y. Weekly production varies from 350 units to 450 units averaging 400 units. Delivery period for both the components is 1 to 3 weeks. The economic is 600 kgs. and for Y is 1,000 kgs. Calculate: (1) Re-order level of X; (ii) Maximum level of X; (iii) Maximum level of Y.
Answers
Answer:
Step-by-step explanation:
To calculate the reorder level of component X, we need to find out the average weekly consumption of X.
Average consumption of X per unit of 'RED' = 0.4 kg
Average weekly production of 'RED' = 400 units
Average weekly consumption of X for producing 400 units of 'RED' = 0.4 kg/unit x 400 units/week = 160 kg/week
Assuming lead time of 3 weeks for delivery of X, the reorder level of X would be:
Reorder level of X = Average weekly consumption of X x Lead time for delivery of X
Reorder level of X = 160 kg/week x 3 weeks = 480 kg
To calculate the maximum level of X, we need to take into account the economic order quantity and the maximum storage capacity.
Economic order quantity of X = Square root of [(2 x Annual consumption of X x Ordering cost per order) / Cost per unit of X]
Assuming 52 weeks in a year:
Annual consumption of X = Average weekly consumption of X x 52 weeks/year = 160 kg/week x 52 weeks/year = 8,320 kg/year
Ordering cost per order of X = 600
Cost per unit of X = 1
Economic order quantity of X = Square root of [(2 x 8,320 kg x 600) / 1] = 2,771.28 kg (approx.)
Maximum storage capacity of X = Economic order quantity of X + Safety stock - Average weekly consumption x Maximum lead time
Assuming a safety stock of 20% of the economic order quantity and a maximum lead time of 3 weeks:
Maximum storage capacity of X = 2,771.28 kg + (0.2 x 2,771.28 kg) - (160 kg/week x 3 weeks) = 2,815.82 kg (approx.)
To calculate the maximum level of Y, we follow the same approach as for X:
Annual consumption of Y = Average weekly consumption of Y x 52 weeks/year
Average consumption of Y per unit of 'RED' = 0.6 kg
Average weekly consumption of Y for producing 400 units of 'RED' = 0.6 kg/unit x 400 units/week = 240 kg/week
Annual consumption of Y = 240 kg/week x 52 weeks/year = 12,480 kg/year
Economic order quantity of Y = Square root of [(2 x Annual consumption of Y x Ordering cost per order) / Cost per unit of Y]
Ordering cost per order of Y = 1,000
Cost per unit of Y = 1.5
Economic order quantity of Y = Square root of [(2 x 12,480 kg x 1,000) / 1.5] = 915.65 kg (approx.)
Maximum storage capacity of Y = Economic order quantity of Y + Safety stock - Average weekly consumption x Maximum lead time
Assuming a safety stock of 20% of the economic order quantity and a maximum lead time of 3 weeks:
Maximum storage capacity of Y = 915.65 kg + (0.2 x 915.65 kg) - (240 kg/week x 3 weeks) = 732.52 kg (approx.)
Compute the missing x and y values so that each ordered pair will satisfy the given equation y=2x+4
Answers
The missing ordered pairs that satisfy the equation y = 2x + 4 are (3, 10) and (2, 8).
The equation given is y = 2x + 4. To compute the missing x and y values, we need to substitute the given ordered pairs into the equation and solve for the missing variable.
Let's assume we have an ordered pair (x, y) that satisfies the equation y = 2x + 4.
For example, let's say one missing value is x = 3. We can substitute this into the equation:
y = 2(3) + 4
y = 6 + 4
y = 10
So, the missing ordered pair is (3, 10).
Similarly, if another missing value is y = 8, we can substitute this into the equation and solve for x:
8 = 2x + 4
4 = 2x
x = 2
So, the missing ordered pair is (2, 8).
In summary, the missing x and y values that satisfy the equation y = 2x + 4 are (3, 10) and (2, 8).
For more questions on equation
https://brainly.com/question/29174899
#SPJ8