A grocery store sells three different quantities of sugar. A 1-pound bag costs $1.05, a 2-pound bag costs
$1.90, and a 3-pound bag costs $2.82. Enter the unit cost in price per pound for each. Complete the
description about how the unit cost changes as the quantity of sugar increases.
Answers
Step-by-step explanation:
a 1-pound bag is, well, 1 pound. so, the unit price is $1.05.
a 2-pound bag has two units of the 1-pound bag. so, the price per 1-pound unit is $1.90/2 = $0.95
a 3-pound bag has three units of the 1-pound bag. so, the price per 1-pound unit is $2.82/3 = $0.94
the unit cost goes down with increased quantity. but the biggest difference is between 1-pound and 2-pound bags. the unit price difference between 2- and 3-pound bags is almost irrelevant.
Related Questions
My checking account balance was $443 on February 1st and $872 on February 7th. Show the rate of change
Answers
Answer:
$61.29 per day.
Step-by-step explanation:
Checking account balance on February 1st: $443
Checking account balance on February 7th: $872
Difference in balances: $872 - $443 = $429
Number of days between February 1st and February 7th: 7 days
Rate of change = Difference in balances / Number of days
Rate of change = $429 / 7 days
To find the rate of change per day, divide the difference in balances by the number of days:
Rate of change = $429 / 7 days ≈ $61.29 per day
Therefore, the rate of change in your checking account balance during that period was approximately $61.29 per day.
If you subtract 0. 3 from a certain number, add 0. 4 times the original number to the result, and then add another 2. 78, you'll get 25. What was the original number?
Answers
After all the conditions you applied from the statement given you will get the original number as 16.08.
What is the algebraic equation?An algebraic equation is when two expressions are set equal to each other, and at least one variable is included.
Given that, if you subtract 0.3 from a certain number, add 0.4 times the original number to the result and then add another 2.78, you'll get 25.
We need to find the original number.
Let us take the original number as x.
Now, subtract 0.3 from the original number.
That is x-0.3.
0.4 times the original number is 0.4x.
Add 0.4 times the original number to the result.
That is, x-0.3+0.4x=1.4x-0.3
Now, add 2.78 to the result. That is 1.4x-0.3+2.78=1.4x+2.48.
As a result, you'll get 25. That is 1.4x+2.48=25
⇒1.4x=22.52
⇒x=16.08
There, the original number is 16.08.
To learn more about algebraic equations visit:
https://brainly.com/question/953809.
#SPJ1
graph h(x)=(x-1)^2-9
Answers
The graph of h(x) = (x-1)^2 - 9 is a U-shaped parabola that opens upwards, with the vertex at (1, -9), and it extends indefinitely in both directions.
The function h(x) = (x-1)^2 - 9 represents a quadratic equation. Let's analyze the different components of the equation to understand the behavior of the graph.
The term (x-1)^2 represents a quadratic term. It indicates that the graph will have a parabolic shape. The coefficient in front of the quadratic term (1) implies that the parabola opens upwards.
The constant term -9 shifts the graph downward by 9 units. This means the vertex of the parabola will be at the point (1, -9).
Based on this information, we can draw the following conclusions:
The graph will be a U-shaped curve with the vertex at (1, -9).
The vertex represents the minimum point of the parabola since it opens upward.
The parabola will be symmetric with respect to the vertical line x = 1 since the coefficient of the quadratic term is positive.
The graph will extend indefinitely in both directions.
To accurately plot the graph, you can choose several x-values, substitute them into the equation to find the corresponding y-values, and then plot the points on the graph. Alternatively, you can use graphing software or calculators that can plot the graph of the equation for you.
Remember to label the axes and indicate the vertex at (1, -9) to provide a complete representation of the graph of h(x) = (x-1)^2 - 9.
for such more question on parabola
https://brainly.com/question/9201543
#SPJ8
To find the number in a square, add the numbers in the two circles
connected to it.
Fill in the missing numbers.

Answers
The missing values in the quantitative reasoning given are : -2, 13 and 9
Given the rule :
square = circle + circleWe can deduce that :
circle = square - circleFor the left circle :
circle = -6 - (-4) = -6 + 4 = -2
For the right circle :
circle = 11 - (-2) = 11 + 2 = 13
For the left square :
square = 13 + (-4)
square = 13 -4 = 9
Therefore, the missing values are : -2, 13 and 9
Learn more on puzzle: https://brainly.com/question/27645967
#SPJ1
The volume of a rectangular prism is 5,890.625 cm3. If the height is 14.5 cm and the length is 25 cm, what is the value of the width?
Answers
Answer:
Step-by-step explanation:
The formula for the volume of a rectangular prism is V = lwh, where V is the volume, l is the length, w is the width, and h is the height.
We know that V = 5,890.625 cm^3, h = 14.5 cm, and l = 25 cm.
Substituting these values into the formula, we get:
5,890.625 = 25w(14.5)
5,890.625 = 362.5w
w = 16.25
Therefore, the width of the rectangular prism is 16.25 cm.
Answer:
It's A
Step-by-step explanation:
well all you have to do is divide like 5,890.625 dvided by 14.5 then divide again by 25 them bam you got 16.25
Can someone please help me ASAP??

Answers
what is the property of 3x(5x7)=(3x5)7
Answers
The property you are referring to is called the associative property of multiplication. According to this property, when multiplying three numbers, the grouping of the numbers does not affect the result. In other words, you can change the grouping of the factors without changing the product.
In the equation you provided: 3x(5x7) = (3x5)7
The associative property allows us to group the factors in different ways without changing the result. So, whether we multiply 5 and 7 first, or multiply 3 and 5 first, the final product will be the same.
Solve the following equation by using the addition principle. Check the solution.
-4/5 + y = -1/4
Answers
Answer:
y = 11/20
Step-by-step explanation:
-4/5 + y = -1/4
Add 4/5 to each side
-4/5 +4/5 + y = -1/4+4/5
y = -1/4 + 4/5
Get a common denominator
y = -1/4 *5/5 + 4/5 *4/4
y = -5/20 + 16/20
y = 11/20
Check
-4/5 +11/20 = -1/4
Get a common denominator
-4/5*4/4 + 11/20 = -1/4*5/5
-16/20 +11/20 = -5/20
-5/20 = - 5/20
Check
Step-by-step explanation:
\( - \frac{4}{5} + y = - \frac{1}{4} \\ y = \frac{ - 1}{4} + \frac{4}{5} \\ y = \frac{ - 5 + 16}{20} \\ y = \frac{11}{20} \)
\(y = \frac{11}{20} \)
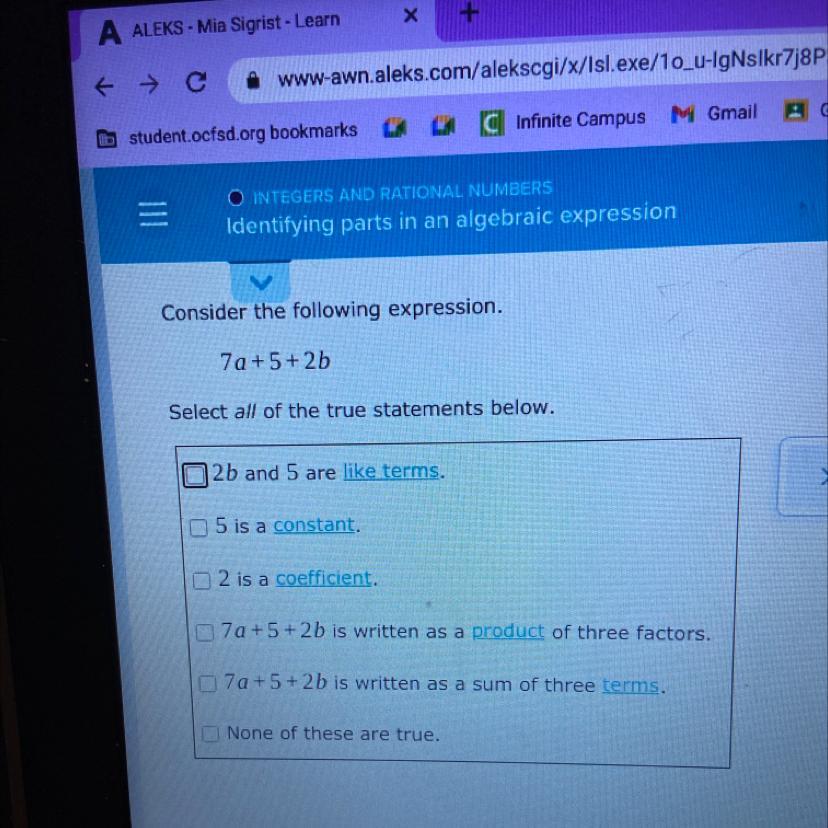
7a +5+2b
Select all of the true statements below.
- 2b and 5 are like terms.
- 5 is a constant.
- 2 is a coefficient.
- 7a+5+2b is written as a product of three factors.
- 7a +5+2b is written as a sum of three terms.
- None of these are true.
Answers
Answer:
5 is a constant
2 is a coefficient
7a + 5 + 2b is written as a sum of three terms
What are the coordinates of the terminal point determined by t = 10pi/3 ?

Answers
The correct option is- A: (-1/2 , -√3/2) are the coordinates found using the terminal points t = 10pi/3.
Explain about the terminal points?On the unit circle, the terminal point. To find any terminal point on the unit circle which start at (1, 0), and determine the angle in degree or radian on the circle that travel counter clockwise whereas if angle is positive as well as clockwise if the angle is negative. The terminal point is the coordinate of the endpoint.
Given values:
t = 10pi/3
convert to degrees
t = 10*pi/3
t = 10*180/3
t = 600 degrees
Find quadrant of 600 degrees.
600 = 360+240
240 comes in III quadrant
Thus, x-coordinate and y-coordinate are negative
Now,
240° = 180°+ 60°
60° is the angle for which terminal point are to be find.
Let ∅=60°
Consider unit circle
radius r = 1 units
Then,
x = -r*cos ∅
x = -cos 60
x = -(1/2)
And,
y = -r*sin ∅
y = -sin 60
y = -(√3)/2
Thus, the coordinates of the terminal point are found as (-1/2 , -√3/2) by
t = 10pi/3.
Know more about the terminal points
https://brainly.com/question/3988149
#SPJ1
The diameter of a circle is 8cm. Find its circumference to the nearest tenth.
Answers
Answer:
\(C = 25.1 \text{ cm}\)
Step-by-step explanation:
We can find the circumference of the circle by plugging the given radius value 8 cm into the formula:
\(C = \pi d\)
Note: This formula can also be written as \(C = 2\pi r\) because \(2r = d\).
↓ plugging in the given radius
\(C = 8\pi \text{ cm}\)
↓ rounding to the nearest tenth
\(\boxed{C = 25.1 \text{ cm}}\)
Question You and a friend tutor for a total of 12 hours. Use the tape diagram to find how many hours you tutor. You tutor for hours.
Answers
The amount of time I spent tutoring from the tape diagram is 4 hours.
How to solve an equationLet x represent one rectangle. Therefore from the tape diagram:
Amount of hours I spent tutoring = x + x = 2x
Amount of hours my friend spent tutoring = x + x + x + x = 4x
Since both me and my friend spent a total of 12 hours, hence:
2x + 4x = 12
6x = 12
Dividing through by 6:
x = 2 hours
Amount of hours I spent tutoring = 2x = 2(2) = 4 hours
The amount of time I tutor is 4 hours.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1

I already tried D but it wasnt correct

Answers
Answer:
A. E bisects AB and CD
Step-by-step explanation:
If E is a bisector, it creates two pairs of congruent sides. The included angles are congruent because they are vertical angles. The triangles will be congruent by SAS.
PLS HELP ILL GIVE YOU FREE PIONTS AND BRAINLEST PLSSS

Answers
Answer:
B,D,C,A,E
Step-by-step explanation:
-1, -4/3, 1/2, 2, 2 1/4
Answer:
BDCAE
Step-by-step explanation:
hope this help
n a box of 12 tape measures, there is one that does not work. Employees take a tape measure as needed. The tape measures are not returned, once taken. You are the 8th employee to take a tape measure. Is this a binomial experiment?
a. Yes, the probability of success is one out of 12 with 8 selected.
b. No, the probability of getting the broken tape measure changes as there is no replacement.
c. Yes, you are finding the probability of exactly 5 not being broken.
d. No, binomial does not include systematic selection such as "eighth".
Answers
Answer:
b. No, the probability of getting the broken tape measure changes as there is no replacement.
Step-by-step explanation:
For each tape measure, there are only two possible outcomes. Either it is broken, or it is not, which means that the first condition for the binomial distribution is respected.
However, the tapes are not returned to the box, which means that in each trial, the probabilities of getting the tape with defect changes, which means that the binomial distribution cannot be used. So option b is the correct answer
Levy is painting a miniature model of a World War II tank. His figure uses a 1:72 scale and is 22.5 cm
long. How many centimeters long was the actual tank?
cm
Answers
Levy is painting a miniature model of a World War II tank. His figure uses a 1:72 scale and is 22.5 cm long. The actual tank is 1620 cm long.
To determine the length of the actual tank, we need to scale up the length of the miniature model using the given scale of 1:72.
Let's denote the length of the actual tank as "x".
According to the scale, 1 cm on the miniature model represents 72 cm on the actual tank.
So, we can set up the following proportion:
1 cm (miniature model) / 72 cm (actual tank) = 22.5 cm (miniature model) / x cm (actual tank)
Cross-multiplying and solving for x, we get:
x = (72 cm * 22.5 cm) / 1 cmx = 1620 cm
The actual tank is 1620 cm long.
For more such questions on miniature model
https://brainly.com/question/14657504
#SPJ8
The luxury Swiss Chalet hotel general manager (GM) reported to her owner that the hotel's Occupancy Index for the calendar year 2019 was 1.25. Based upon only this information alone, what MUST be correct?
Answers
Answer:
the Swiss Chalet had higher occupancy than its competitive set in 2019
Step-by-step explanation:
15–80÷4^2×2 as a expression using the order of operations.
Answers
\(\huge\text{Hey there!}\)
\(\large\textsf{Do PEMDAS}\)
\(\large\text{Parentheses}\)
\(\large\text{Exponents}\)
\(\large\text{Multiplication}\)
\(\large\text{Division}\)
\(\large\text{Addition}\)
\(\large\text{Subtraction}\)
\(\mathsf{15 - 80\div4^2\times2}\)
\(\mathsf{4^2}\)
\(\mathsf{= 4\times 4}\)
\(\mathsf{= \bf 16}\)
\(\mathsf{15 - 80\div16\times 2}\)
\(\mathsf{80\div16}\)
\(\mathsf{= \bf 5}\)
\(\mathsf{15 - 5\times2 }\)
5 × 2 = 10
\(\mathsf{15 - 10}\)
\(\mathsf{= \bf 5}\)
\(\boxed{\boxed{\large\textsf{Answer: \huge \bf 5}}}\huge\checkmark\)
\(\text{Good luck on your assignment and enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
The number of children's books at a library was 2/5 of the total number of books. After 298 children's books were added to the library, the number of children's books was 4/7 of the total number of books. How many books were there in the library at first?
Answers
Answer:
745
Step-by-step explanation:
You want the original number of books in the library if adding 298 children's books increased the fraction of children's books from 2/5 to 4/7.
RatioWe often like to work problems like this in terms of "ratio units." Here, we'll let x represent the number of books in a ratio unit. This means the number of children's books is originally 2x, and the total number of books is originally 5x. Then we have ...
(2x +298)/(5x +298) = 4//7
SolutionCross multiplying gives ...
7(2x +298) = 4(5x +298)
3(298) = 6x . . . . . . . . . . . . . subtract (14x+4(298))
149 = x
745 = 5x . . . . . . the original number of books in the library
There were 745 books in the library at first.
__
Additional comment
If we let x represent the original number of library books, then the arithmetic involves more fractions. You would have an equation like ...
2/5x +298 = 4/7(x +298)
<95141404393>
A sample of a radioactive substance has an initial mass of 45.1 mg. This substance follows a continuous exponential decay model and has a half-life of 19
minutes.
(a)let t be the time (in minutes) since the start of the experiment, and
let y be the amount of the substance at time t.
Write a formula relating y to t.
Use exact expressions to fill in the missing parts of the formula.
Do not use approximations.
y = ()e^()t
(b) How much will be present in 9 minutes?
Do not round any intermediate computations, and round your
answer to the nearest tenth.
Answers
a) The formula relating y to t is: y = 45.1 * e^(-0.693/19 * t) b) there will be approximately 30.1 mg of the substance present after 9 minutes.
How to Write a formula relating y to t.(a) The general formula for exponential decay is y = y0 * e^(-kt), where y is the amount at time t, y0 is the initial amount, k is the decay constant, and e is Euler's number.
To find the decay constant, we can use the fact that the half-life is 19 minutes. The formula for half-life is t1/2 = ln(2) / k, where ln(2) is the natural logarithm of 2.
Substituting t1/2 = 19 and ln(2) = 0.693 into the formula gives:
19 = 0.693 / k
k = 0.693 / 19
So the formula relating y to t is:
y = 45.1 * e^(-0.693/19 * t)
(b) To find how much will be present in 9 minutes, we can plug t = 9 into the formula we found in part (a):
y = 45.1 * e^(-0.693/19 * 9) ≈ 30.1 mg
So, there will be approximately 30.1 mg of the substance present after 9 minutes.
Learn more about exponential decay model at https://brainly.com/question/29629074
#SPJ1
Anyone that helps me with getting all these answers, will get a brainliest (correct answers only)

Answers
Answer:
58) 12.65
59) 8.25
60) 17.89
61) 15.81
62) 4.27
63) 10.07
64) a=4, ST=48
65) x=11, ST=22
66) Yes because the feet are like points on a plane and the ground would be the coordinate plane
67) 4 1/2 feet
68) 0.275
69) 56
Step-by-step explanation:
I hope this helps!!
Find the area of the triangle.
18 in.
25 in.

Answers
Answer:
225in
Step-by-step explanation:
Basically multiply 18*25
Your answer will be 450
Then simply divide it by 2
You’ll get your answer, hope I could help
2 The driver of the water tanker works for 5% days per week and 9 hours per day on week days except on Saturdays where they work for a ½ day (4,5 hours). The rate per hour was R92,50 and the rate of pay was doubled on Saturdays. 2.1 Calculate the amount of money that the tanker driver receive per day during week days. 2.2 Determine the total number of hours that the driver has worked in March 2022. (2) (3) Page | 2
Answers
From the mathematical problem, the tanker driver receives R749,25 per day during week days and the driver worked a total of 261 hours in March 2022.
How is the Problem Calculated?2.1 To calculate the amount of money that the tanker driver receives per day during week days, we need to calculate the total number of hours worked during a weekday and multiply it by the hourly rate, which is R92,50.
On weekdays, the driver works for 9 hours per day for 5% days per week, except for Saturdays where they work for 4.5 hours. So the number of hours worked during a weekday is:
9 hours/day x 5 days/week = 45 hours/week
45 hours/week - 4.5 hours on Saturday = 40.5 hours/week
To calculate the amount of money earned per day, we divide the weekly pay by the number of weekdays in a week:
Pay per week = 40.5 hours/week x R92,50/hour = R3746,25/week
Pay per day = R3746,25/week ÷ 5 days/week = R749,25/day
Therefore, the tanker driver receives R749,25 per day during week days.
2.2 To determine the total number of hours that the driver has worked in March 2022, we need to know the number of weekdays in March 2022.
March 2022 has 31 days, so the number of weekdays in March 2022 is:
31 days in March 2022 - 4 Saturdays = 27 weekdays in March 2022
Now we can calculate the total number of hours worked in March 2022:
Total hours worked in March 2022 = 27 weekdays x 9 hours/weekday + 4.5 hours on each Saturday x 4 Saturdays
Total hours worked in March 2022 = 243 hours + 18 hours
Total hours worked in March 2022 = 261 hours
Therefore, the driver worked a total of 261 hours in March 2022.
Learn more about mathematical problems here: https://brainly.com/question/22688504
#SPJ1
hi why do we need to keep watching ads tbh im very tired of it
Answers
Answer:
cs sometimes we needa pass a test n dis is the only shi dat b righh fr
Step-by-step explanation:
What is the amplitude ? How do I find it? do I add 7.7 to (-6.7) then divide? Thank you in advance

Answers
Answer:
7.2
Step-by-step explanation:
The amplitude is half the difference between the maximum and the minimum.
A = (7.7 − (-6.7)) / 2
A = 7.2
Correct answer please

Answers
Answer:
50.75
Step-by-step explanation:
We have:
\(E[g(x)] = \int\limits^{\infty}_{-\infty} {g(x)f(x)} \, dx \\\\= \int\limits^{1}_{-\infty} {g(x)(0)} \, dx+\int\limits^{6}_{1} {g(x)\frac{2}{x} } \, dx+\int\limits^{\infty}_{6} {g(x)(0)} \, dx\\\\= \int\limits^{6}_{1} {g(x)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {(4x+3)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {(4x)\frac{2}{x} } \, dx + \int\limits^{6}_{1} {(3)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {8} \, dx + \int\limits^{6}_{1} {\frac{6}{x} } \, dx\\\\\)
\(=8\int\limits^{6}_{1} \, dx + 6\int\limits^{6}_{1} {\frac{1}{x} } \, dx\\\\= 8[x]^{^6}_{_1} + 6 [ln(x)]^{^6}_{_1}\\\\= 8[6-1] + 6[ln(6) - ln(1)]\\\\= 8(5) + 6(ln(6))\\\\= 40 + 10.75\\\\= 50.74\)
Thompson and Thompson is a steel bolts manufacturing company. Their current steel bolts have a mean diameter of 145 millimeters, and a standard deviation of 7 millimeters. If a random sample of 31 steel bolts is selected, what is the probability that the sample mean would be less than 141.5 millimeters? Round your answer to four decimal places.
Answers
Using a standard normal distribution table, we find that the probability is approximately 0.0134 (rounded to four decimal places).
What is probability?Probability is a measure of the likelihood or chance that a particular event or outcome will occur. It is expressed as a value between 0 and 1, where 0 represents an event that is impossible to occur, and 1 represents an event that is certain to occur.
According to question:To solve this problem, we can use the formula for the standard deviation of the sample mean:
Standard deviation of sample mean = standard deviation / √(sample size)
Plugging in the given values:
Standard deviation of sample mean = 7 / √(31)
Next, we can calculate the z-score, which is the number of standard deviations the sample mean is below the population mean:
z-score = (sample mean - population mean) / standard deviation of sample mean
Plugging in the given values:
z-score = (141.5 - 145) / (7 / √(31))
Using a calculator, we find that the z-score is approximately -2.22.
Finally, we can use a standard normal distribution table or a calculator to find the probability that a z-score is less than -2.22.
Using a standard normal distribution table, we find that the probability is approximately 0.0134 (rounded to four decimal places).
To know more about probability visit:
https://brainly.com/question/30034780
#SPJ1
Question 21 ptsA rectangular prism has a volume of 3 m3, a length of 30 cm, and a width of40 cm. What is the height of the prism?25 m250 cm25 cm0.25 cm
Answers
We have a rectangular prism and we are given the following information.
\(\begin{gathered} A=3m^3 \\ L=30\operatorname{cm} \\ W=40\operatorname{cm} \end{gathered}\)We are asked to find the height of the rectangular prism
\(H=\text{?}\)The very first thing to notice is that the given area and the given length, width has different units.
It is very important to have the same unit throughout otherwise there is a chance of making a mistake!
So let us first convert the given area from m into cm.
We know that 1 meter is equal to 100 centimeters.
\(A=3\cdot100=300\operatorname{cm}\)Now we can proceed to find the height of the prism.
Recall that the area of a rectangular prism is given by
\(A=W\cdot L\cdot H\)Where W is the width, L is the length and H is the height of the rectangular prism.
Finally, just substitute the given values into the above equation and solve for H.
\(\begin{gathered} 300=40\cdot30\cdot H \\ H=\frac{300}{40\cdot30} \\ H=\frac{300}{1200} \\ H=\frac{1}{4} \\ H=0.25\operatorname{cm} \end{gathered}\)Therefore, the height of the rectangular prism is 0.25 cm.
The correct option is the last one 0.25 cm.
What is happening to the pieces (units) when the numerator and denominator are getting larger?
I NEED HELP!!!!!!
Answers
Answer:
the number itself, (units) are getting bigger
Step-by-step explanation:
-10 degrees Celsius is what Fahrenheit
Answers
Answer:
Step-by-step explanation:
i think if its -10 degrees i think the fahrenheit would be 50 degrees