A mechanic had412 gallons of motor oil at the start of the day. At the end of the day, only 5 pints remained
Answers
The mechanic used 412 - 411.375 = 0.625 gallons of motor oil during the day.
A mechanic had 412 gallons of motor oil at the start of the day and ended up with only 5 pints of oil remaining.To solve this problem, we need to convert both measurements to the same unit.
1 gallon = 8 pints (since there are 8 pints in a gallon)
So the mechanic started with:
412 gallons * 8 pints/gallon = 3,296 pints
And ended with:
5 pints
To find how much motor oil the mechanic used during the day, we can subtract the ending amount from the starting amount:
3,296 pints - 5 pints = 3,291 pints
To convert this back to gallons, we divide by 8:
3,291 pints / 8 pints/gallon = 411.375 gallons (rounded to three decimal places)
Learn more about measurements
brainly.com/question/2107310
#SPJ11
Related Questions
a spinner has three sections. the table shows the results of spinning the arrow on the spinner 80 times. what is the experimental probability of the arrow stopping over section 1? responses 128 1 over 28 720 7 over 20 713 7 over 13 45 4 over 5 section 1section 2section 3 283616
Answers
The experimental probability of the arrow stopping over section 1 is 7/13, or 0.538.
To calculate this, you need to take the number of times the arrow stopped on section 1 (45) and divide it by the total number of times the arrow was spun (80). This can be expressed as a fraction (45/80), which can be simplified to 7/13. To convert this fraction to a decimal, divide the numerator by the denominator (7/13 = 0.538).
for more questions related to experimental probability, refer here:
https://brainly.com/question/30694293#
#SPJ11
The box-and-whisker plot below represents some data set. What percentage of the data values are greater than or equal to 92?
Answers
The percentage of the data values in the box-and-whiskers plot, that are greater than or equal to 92, which is the 75th percentile, based on the five number summary, are 25 percent of the data.
What is the five number summary of a box-and-whiskers plot?The five number summary of a box-and-whiskers plot are value of the minimum, the first quartile, the median, the third quartile and the maximum value of the set of data.
Please find attached the possible box-and-whiskers plot in the question, obtained from a similar question on the internet
The five number summary from the box-and-whiskers plot are;
Minimum value = 82
The first quartile or the 25th percentile = 87
The median, second quartile or the 50th percentile = 90
The third quartile or the 75th percentile = 92
The value 92 on the data represents the 75th percentile, therefore, the percentage of the data that are greater than or equal to 92 are; 100 - 75 = 25 percent
Learn more on box-and-whiskers plots here: https://brainly.com/question/973515
#SPJ1

help..............solve for x give answer as an improper fraction

Answers
The appropriate fraction produced by the expression is -32/9.
Solving rational fractionsAny function that can be expressed as a rational fraction, which is an algebraic fraction in which both the numerator and the denominator are polynomials, is referred to as a rational function.
Given the function below:
6x-5/3 = 5x + 9
Cross multiply
6x - 5 = 3(5x + 9)
Expand to have:
6x - 5 = 3(5x) + 3(9)
6x - 5 = 15x + 27
6x - 15x = 27 + 5
-9x = 32
Divide both sides by -9
-9x/-9 = 32/-9
x = -32/9
Hence the result of the expression as an improper fraction is -32/9.
Learn more on rational fraction here: https://brainly.com/question/19044037
#SPJ1
6) How long will it take for an investment to double in value if it earns 4.75% compoundedcontinuously?A) 14.593 yearsB) 15.711 years C) 23.129 years D) 7.296 years
Answers
A quantity that is compounded continuously follows the next equation:
\(A=Pe^{rt}\)Where:
\(\begin{gathered} A=\text{ amount in time ''t''} \\ P=\text{ initial amount} \\ r=\text{ rate of interest in decimal form} \\ t=\text{ time} \end{gathered}\)Now, the interest rate in decimal notation is determined by dividing the percentage by 100:
\(r=\frac{4.75}{100}=0.0475\)Now, we are asked to determine the time required for the quantity to double. Therefore, we need to determine "t" when:
\(A=2P\)Substituting in the formula we get:
\(2P=Pe^{rt}\)Now, we can cancel out the "P":
\(2=e^{rt}\)Now, we solve for "t". First, we take the natural logarithm to both sides:
\(ln2=lne^{rt}\)Now, we use the following property of logarithms:
\(lnx{}^y=ylnx\)Applying the property we get:
\(ln2=rtlne\)We have that:
\(lne=1\)Therefore:
\(ln2=rt\)Now, we divide both sides by "r":
\(\frac{ln2}{r}=t\)Now, we substitute the value of "r":
\(\frac{ln2}{0.0475}=t\)Solving the operations:
\(14.593=t\)Therefore, the right option is A.
A particle moving along a curve in the xy-plane has position.
Answers
The position of a particle moving along a curve in the xy-plane can be described using parametric equations, where x and y are both functions of a third variable, usually time (t).
1. Parametric equations are equations that express the coordinates of a point (x, y) in the xy-plane in terms of a single variable, often time (t). In this case, x = f(t) and y = g(t), where f(t) and g(t) are functions of time.
2. To find the position of the particle at any given time, plug the value of time (t) into both functions, f(t) and g(t), to find the corresponding x and y coordinates. The position of the particle at time t is given by (x(t), y(t)).
3. To visualize the path of the particle, you can plot the curve described by the parametric equations x = f(t) and y = g(t) on the xy-plane. The particle moves along this curve as time progresses.
4. If you need to find the particle's velocity or acceleration, you can calculate the first and second derivatives of the position functions with respect to time.
In summary, the position of a particle moving along a curve in the xy-plane can be described by parametric equations, which relate the x and y coordinates to a third variable, usually time (t). The position of the particle at any given time can be found by plugging in the value of time into the parametric equations.
To know more about Parametric equations visit:
brainly.com/question/29187193
#SPJ11
Given the polynomial: f(x) = 3x² + x + 9, find f(-5).
Answers
Answer:
79.
Step-by-step explanation:
Replace the x by -5 and simplify:
f(-5) = 3(-5)^2 + (-5) + 9
= 75 - 5 + 9
= 79.
The value of f(-5) will be 79.
Step-by-step explanation:
An expression of more than two algebraic terms, especially the sum of several terms that contain different powers of the same variable(s) is called a polynomial.
The following table gives special names given to polynomials of low orders.
polynomial order polynomial name
2 quadratic polynomial
3 cubic polynomial
4 quartic
5 quintic
6 sextic
Here, the given polynomial: f(x) = 3x² + x + 9
by putting value of x = -5
\(3*(-5)^{2} + (-5) + 9\)
after putting we get,
\(75 - 5 + 9\)
On solving the above numerical we get,
\(79\).
So our final answer would be 79 on putting x = -5 in the given polynomial : f(x) = 3x² + x + 9
To learn more about polynomials, visit :
https://brainly.com/question/11536910?referrer=searchResults
Simplify 5 x times the square root of quantity 3 x end quantity minus 2 x times the square root of quantity 3 x end quantity minus x times the square root of quantity 3 x end quantity period.
Answers
Simplifying the expression gives 6x√3x
How to simplify the expressionAdding and subtracting surds is applicable where the numbers underneath the root symbols also known as radicands are the same.
From the information given, we have:
5x √3x + 2x√3x - x√3x
We can see than the numbers within the root symbols '3x' are the same for all the three surds.
Note that if the root cases are the same, the numbers cannot be added or substracted.
Now, let's add the values outside the roots
5x √3x + 2x√3x - x√3x
= 5x + 2x - x
= 7x - x
= 6x
We have;
6x√3x
Thus, simplifying the expression gives 6x√3x
Learn more about surds here:
https://brainly.com/question/840021
#SPJ1
assume the mass hanger (before we add anything to it) is about 5g. how much mass will you need to add to the mass hanger in order to get a total single mass hanger system equal to 90 grams?
Answers
We will need to add 85 grams of mass to the mass hanger in order to get a total single mass hanger system equal to 90 grams.
To get a total single mass hanger system equal to 90 grams, you will need to add 85 grams of mass to the mass hanger. This is because the mass hanger is already 5 grams, and you need to add enough mass to get to 90 grams.
Here's the step-by-step explanation:
1. Start with the mass of the mass hanger: 5 grams
2. Subtract this from the desired total mass: 90 grams - 5 grams = 85 grams
3. The result is the amount of mass you need to add to the mass hanger: 85 grams
The combination of slotted masses and mass hanger allows a student to quickly create any desired amount of mass.
Know more about mass hanger here:
https://brainly.com/question/2264725
#SPJ11
someone know the answer
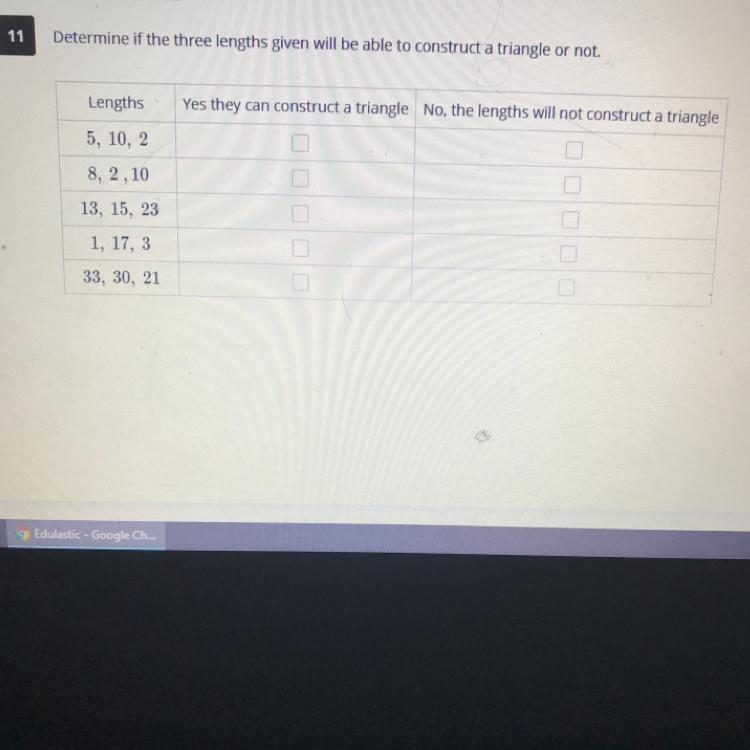
Answers
Answer:
yes all
Step-by-step explanation:
What is a mathematical operation that is easily performed but that is highly unlikely to reverse in a reasonable amount of time
Answers
A mathematical operation that is easily performed but highly unlikely to reverse in a reasonable amount of time is known as a "one-way function." One-way functions are fundamental to cryptography, particularly in areas like secure hashing and public-key encryption. These functions are designed to be simple and efficient to compute in one direction but extremely difficult and time-consuming to reverse.
A prime example of a one-way function is the multiplication of two large prime numbers. Multiplying them is a straightforward task, but attempting to factorize the product back into its original primes, known as the "prime factorization problem," is considered computationally infeasible for large numbers. This asymmetry in complexity is utilized in cryptographic systems, such as the RSA encryption algorithm, to ensure the security of sensitive information.
In summary, one-way functions are mathematical operations that can be easily performed but are highly challenging to reverse. Their properties make them invaluable in the realm of cryptography, where they provide the foundation for secure communication and data protection.
To know more about mathematical operation visit:
https://brainly.com/question/20628271
#SPJ11
I NEED EXTREME HELP. I ASKED THIS QUESTION 2 TIMES ALREADY AND NOW THIS IS MY THIRD. WHOEVER ANSWERS THIS CAN ANSWER THE SAME THING ON MY PROFILE AND GET A LOT OF POINTS. HELP!!!!!

Answers
Answer:
2.5 times taller
Step-by-step explanation:
6+6=12 3+3=6 12+6=18 so the streetlight is 18 ft
What value of q is a solution to this equation?
-3(12+q)=-18
Answers
Answer: q= -6
Step-by-step explanation:
Find the percent increase in volume when 1 foot is added to each dimension of the prism. Round your answer to the nearest tenth of a percent. 100 points!!!

Answers
Step-by-step explanation:
4 × 11 = 44
44 × 9 = 396
therefore it is 396ft
Answer:
4 x 11 = 44
44 x 9 = 396
It will be 396 ft
Step-by-step explanation:
Jon is hitting baseballs. The height of the ball is given by h(t) = - 16t? + 5t + 5 where t is in
seconds. When will the baseball hit the ground?
Answers
Your equation is wrong. See below for correct equation.
The ball will hit the ground when h(t) is 0.
Here is the set up:
0 = -16t^2 + 5t + 5
Solve for t to find your answer.
Rewrite the following equation in slope-intercept form. Y + 5 = 1 7 ( x + 7 )
Answers
Answer: y = 17x + 114
Step-by-step explanation:
The equation for the slope-intercept form is y = mx + b.
Arrange the equation so that it resembles y = mx + b.
You will do this by multiplying and subtracting so y is on the left side of the equation and mx + b is on the right side of the equation.
y + 5 = 17(x + 7)
y + 5 = 17x + 119
y + 5 - 5 = 17x + 119 - 5
y = 17x + 114
Answer:
Y = 17x + 114
Step-by-step explanation:
1. Y + 5 = 17 (x+7)
2. Y + 5 = 17x + 119 [Multiply the numbers in parenthesis by 17.]
3. Y = 17x + 114. [To keep the balance and move the 5 over, subtract it from 119.]
Cuánto es -a +28 =14
Answers
a = -14
-14+28= 14
14 x 2 = 28
1/2 of -28 --> -14
This means a equals -14.
Esto significa A=-14
(sorry my spanish is not good, hope this helps)
Find the volume of a right circular cone that has a height of 14.9 cm and a base with a circumference of 2.9 cm. Round your answer to the nearest tenth of a cubic centimeter
Answers
The volume of the right circular cone is approximately 1.6 cubic centimeters (rounding this answer to the nearest tenth of a cubic centimeter).
What is volume ?
Volume is a physical quantity that measures the amount of three-dimensional space that a substance or object occupies.
The volume of a right circular cone is given by the formula
\(V = (1/3)\pi r^2h\) , where r is the radius of the base and h is the height of the cone. We are given the height of the cone, which is 14.9 cm. To find the radius of the base, we need to use the given circumference of the base, which is 2.9 cm.
The formula for the circumference of a circle is C = 2πr, where C is the circumference and r is the radius. We can rearrange this formula to solve for r, which gives us r = C/(2π). Plugging in the given circumference of 2.9 cm, we get:
r = 2.9/(2π) ≈ 0.461
Now, we can substitute the values of r and h into the formula for the volume of a cone and solve for V:
V = (1/3)π(\(0.461^2\))(14.9) ≈ 1.564 \(cm^3\)
Rounding this answer to the nearest tenth of a cubic centimeter gives us a final volume of approximately \(1.6 cm^3\). Therefore, the volume of the right circular cone is approximately 1.6 cubic centimeters.
To learn more about circumference from the given link :
https://brainly.com/question/28757341
#SPJ1
convex quadrilateral has and . diagonals and intersect at , , and triangles and have equal areas. what is ?
Answers
Triangle AED and triangle BEC have equal areas. The length of AE can be represented as 14 - x (since AC = 14). AE is equal to 10.
To find the length of AE, we can use the fact that triangle AED and triangle BEC have equal areas. Since the areas of two triangles with the same height are proportional to their base lengths, we can set up the following proportion:
Area of triangle AED / Area of triangle BEC = AE / EC
Let's denote EC as x (the length of EC). Then, the length of AE can be represented as 14 - x (since AC = 14).
Now, let's look at the given information about the lengths of the sides of the quadrilateral:
AB = 9
CD = 12
AC = 14
We can use the given information to find the lengths of the other sides of the quadrilateral:
BC = AC - AB = 14 - 9 = 5
AD = AC - CD = 14 - 12 = 2
Next, we can calculate the areas of triangle AED and triangle BEC using the lengths of their sides:
Area of triangle AED = (1/2) * AD * AE
Area of triangle BEC = (1/2) * BC * EC
Since the areas of the two triangles are equal, we can set up the following equation:
(1/2) * AD * AE = (1/2) * BC * EC
Plugging in the values we know:
(1/2) * 2 * (14 - x) = (1/2) * 5 * x
Simplifying the equation:
14 - x = (5/2) * x
Multiplying both sides by 2 to clear the fraction:
28 - 2x = 5x
Adding 2x to both sides:
28 = 7x
Dividing both sides by 7:
x = 4
Therefore, the length of EC is 4.
Since AE = AC - EC, we can calculate AE:
AE = 14 - EC = 14 - 4 = 10
So, AE is equal to 10.
To learn more about triangles visit:
brainly.com/question/11070154
#SPJ11
The complete question is:<Convex quadrilateral ABCD has AB = 9 and CD = 12. Diagonals AC and BD intersect at E, AC = 14 and triangle AED and triangle BEC have equal areas. What is AE?>
Dana has to pay 25% tax on any income above £24,000 per year. Dana is paid £36,000 annually. Calculate the amount of money she receives after tax each month.
Answers
Answer:
£2,750
Step-by-step explanation:
Tax rule: 25% tax on any income above £24,000 per year
It means that upto £24,000 there is no tax and the amount above £24,000
is taxable.
Annual payment of Dana = £36,000
Hence, she will be taxed only on amount above £24,000 out of £36,000.
Lets find amount above £24,000 = £36,000- £24,000 = £12,000
Tax on £12,000 = 25% of £12,000 = 25/100 * £12,000 = £3,000
Thus, £3,000 will be deducted as tax annually out of total earning of £36,000.
Amount paid to Dana after deduction of tax annually = £36,000 - £3,000
Amount paid to Dana after deduction of tax annually is £33,000
As one year has 12 months , hence it can be also said that in 12 months she is paid £33,000
the amount of money she receives after tax in 12 month = £33,000
Dividing LHS and RHS by 12
The amount of money she receives after tax in 12/12 month = £33,000/12
The amount of money she receives after tax in 1 month = £2,750
The amount of money Dana receives after tax each month is £2,750.
Divide g by seven than multiply by six
Answers
Answer:
6/7x
Step-by-step explanation:
g/7 x 6 = 6/7 x
Answer: g / 7 x 6
Explanation:
Statistical data of car accidents show that the annual vehicle miles (i.e., miles per vehicle per year) driven between traffic accident can be presented by a mean of 15,000 miles per year and standard deviation of 3750 miles per year. Z distribution.pdf For a typical driver who drives less than 10,000 miles per year, the probability of him/her having an accident in a year is _____________.
Answers
The probability of a typical driver who drives less than 10,000 miles per year having an accident in a year is 9.18%.
To calculate the probability of a driver who drives less than 10,000 miles per year having an accident, we can use the Z-score and the standard normal distribution.
First, we need to calculate the Z-score for a driver who drives less than 10,000 miles per year. The Z-score formula is:
Z = (X - μ) / σ
Where:
X is the value we want to calculate the Z-score for (10,000 miles per year),
μ is the mean (15,000 miles per year), and
σ is the standard deviation (3,750 miles per year).
Plugging in the values, we get:
Z = (10,000 - 15,000) / 3,750
Z = -1.333
Looking up the Z-score -1.333 in the standard normal distribution table, we find the probability to be approximately 0.0918 or 9.18%.
Therefore, the probability of a typical driver who drives less than 10,000 miles per year having an accident in a year is approximately 9.18%.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ4
Which of the following statements is true?
a. sin 18° = cos 720
b. sin 55° = cos 55°
C. sin 72° = cos 18°
d. Both a and c.
Answers
Answer:
C
Step-by-step explanation:
A) not true. Sin A = some decimal
Cos 720 = 1
D) That means that d is not true either. not true
B) Sin55 = cos55 is not true either only sin(45) = cos(45) is true. So B is not true.
That leaves C. I think if you check it, you'll find it is right. sin(A) = cos(90 - A)
3) Find the linearization L(x) of the function at a. f(x)= cosx, a= pi/2
Answers
Therefore, the linearization of f(x) = cos(x) at a = π/2 is L(x) = π/2 - x.
The linearization of a function f(x) at a point a is given by:
L(x) = f(a) + f'(a)(x - a)
where f'(a) denotes the derivative of f(x) evaluated at x = a.
In this case, we have:
f(x) = cos(x)
a = π/2
First, let's find f'(x):
f'(x) = -sin(x)
Then, we can evaluate f'(a):
f'(π/2) = -sin(π/2) = -1
Next, we can plug in the given values into the formula for linearization:
L(x) = f(a) + f'(a)(x - a)
L(x) = cos(π/2) + (-1)(x - π/2)
L(x) = 0 - x + π/2
L(x) = π/2 - x
To know more about linearization,
https://brainly.com/question/27749345
#SPJ11
A supercomputer system has 50 jobs in the queue that will be executed in sequence. The times required to execute the jobs are independent and follow a common distribution that has mean 20 seconds and standard deviation 4 seconds. Approximate the probability that the supercomputer system will complete executing at least 25 of the jobs in the first 450 seconds.[Use the Central Limit Theorem]
Answers
The probability that the supercomputer system will complete executing at least 25 of the jobs in the first 450 seconds is approximately 0.9599, using the Central Limit Theorem.
Let X be the total time required to execute all the 50 jobs. Then, X follows a normal distribution with mean μ = 50 × 20 = 1000 seconds and standard deviation σ = 50 × 4 = 200 seconds, since the times required for each job are independent and identically distributed.
Now, let Y be the total time required to execute the first 25 jobs. Then, Y also follows a normal distribution with mean μ_Y = 25 × 20 = 500 seconds and standard deviation σ_Y = sqrt(25) × 4 = 20 seconds, since the times required for each job are independent and identically distributed.
To approximate the probability that the supercomputer system will complete executing at least 25 of the jobs in the first 450 seconds, we need to standardize the random variable (Y - μ_Y) / σ_Y and use the standard normal distribution.
P(Y >= 450) = P((Y - μ_Y) / σ_Y >= (450 - 500) / 20) = P(Z >= -2) = 0.9772
Therefore, the probability that the supercomputer system will complete executing at least 25 of the jobs in the first 450 seconds is approximately 0.9599, which is the complement of 0.9772.
For more questions like Probability visit the link below:
https://brainly.com/question/15198684
#SPJ11
Is this relation a function? Justify your answer.

Answers
Answer:
yes
Step-by-step explanation:
yes the answer is A hope this helps
3 An art class is making mosaics with glass squares. Each of the 121 students will get the same number of glass squares to use. The total number of glass squares for the students to use is shown. How many glass squares will each student get? A. Write an expression that can be used to find the number of glass squares each student will receive. B. Complete the given division problem to find the number of squares each student will receive. C. How many whole glass squares will each student receive? 1,240 glass squares D. A remainder is the amount left over when an amount cannot be divided equally. What does the remainder mean in this context? 121)1240 30 R
Answers
Answer: A. To find the number of glass squares each student will receive, we need to divide the total number of squares by the number of students.
We can write this as:
x = number of glass squares per student
x = 1240 / 121
B. To find the number of squares each student will receive, we need to solve for x by dividing 1240 by 121.
1240 ÷ 121 = 10.246753246753247
C. Each student will get 10 whole glass squares.
D. The remainder in this context is the number of glass squares that cannot be distributed evenly among the students. In this case, the remainder is 30. It means that there will be 30 glass squares left over after each student has received 10 squares. It's like remainder in division where after dividing 1240 by 121 the quotient is 10 and the remainder is 30.
Step-by-step explanation:
-4 2/3 as a decimal can't figure it out help!!!
Answers
Answer:
-4.6 Repeating
Step-by-step explanation:
This will be a repeating Decimal. :)
Answer:
0.6666
Step-by-step explanation:
you divide 2 by three and then you get your answer
In triangle ABC, angle a equals 25°, angle C equals 55°, and a B equals 60
Answers
Answer:
7250
Step-by-step explanation:
This is like the pythagorean theorem. So you add A^2,B^2, and C^2. So 25^2 + 60^2 + 55^2. 625 + 3600 + 3025. That equals to 7250.
Which value of t makes the two matrices inverses of each other?
Answers
Answer:
C) 2
Step-by-step explanation:
I got it right on Edge 2021
The reason is that you can see that on the first matrix a and d are the same number, meaning that a and d on the second matrix need to be the same as well. Brainliest please :)
Ignore grammar and spelling mistakes
Answer: 2
Step-by-step explanation:
Southeastern Bell stocks a certain switch connector at its central warehouse for supplying field service offices. The yearly demand for these connectors is 15,000 units. Southeastern estimates its annual holding cost for this item to be $25 per unit. The cost to place and process an order from the supplier is $75. The company operates 300 days per year, and the lead time to receive an order from the supplier is 2 working days.a)Find the economic order quantity.b) Find the annual holding costs.c) Find the annual ordering costs.d) What is the reorder point?
Answers
a) The economic order quantity is 300 units.
b) The annual holding costs are 3,750.
c) The annual ordering costs are 3,750.
d) The reorder point is 117 units.
To solve this problem, we can use the Economic Order Quantity (EOQ) model, which helps determine the optimal order quantity to minimize total inventory costs. The formula for EOQ is:
\(EOQ = \sqrt{((2DS/H)}\)
where D is the annual demand, S is the setup cost per order, and H is the annual holding cost per unit.
a) Find the economic order quantity:
D = 15,000 units
S = 75 per order
H = 25 per unit per year
Substituting into the formula for EOQ:
\(EOQ = \sqrt{((2\times15000\times75)/25)} = \sqrt{90000} = 300 units\)
Therefore, the economic order quantity is 300 units.
b) Find the annual holding costs:
To find the annual holding costs, we need to multiply the average inventory level by the holding cost per unit. Half of the EOQ can be used to compute the average inventory level.
Average inventory level = \(EOQ/2 = 300/2 = 150 units\)
Annual holding costs = Average inventory level x Annual holding cost per unit
= \(150 \times25 = 3,750\)
Therefore, the annual holding costs are 3,750.
c) Find the annual ordering costs:
To find the annual ordering costs, we need to divide the annual demand by the EOQ and then multiply by the setup cost per order:
Number of orders per year = Annual demand / EOQ =\(15,000 / 300 = 50\) orders per year
Annual ordering costs = Number of orders per year x Setup cost per order
=\(50 \times75 = 3,750\)
Therefore, the annual ordering costs are 3,750.
d) What is the reorder point?
The inventory level at which a new order ought to be placed is known as the reorder point. It is calculated as the lead time demand plus safety stock. The lead time demand is the demand during the lead time, which is 2 working days in this case. We can assume that the demand is evenly distributed over the 300 working days per year, so the lead time demand is:
Lead time demand = (Annual demand / 300) x Lead time = \((15,000 / 300) \times 2 = 100 units\)
The safety stock is the buffer inventory kept to cover unexpected demand during the lead time. The safety stock depends on the desired service level and the variability of demand and lead time. Assuming a 95% service level and a normal distribution of demand and lead time, we can use the z-score corresponding to a 95% service level, which is 1.645. The standard deviation of demand during the lead time can be estimated as the square root of the lead time demand:
Standard deviation of demand during lead time = \(\sqrt{100}\) = 10 units
The safety stock is then:
Safety stock = z-score x Standard deviation of demand during lead time
= \(1.645 \times 10 = 16.45\) units (rounded up to 17 units)
Therefore, the reorder point is:
Reorder point = Lead time demand + Safety stock
= \(100 + 17 = 117\)units
Therefore, the reorder point is 117 units.
for such more question on reorder point
https://brainly.com/question/26814787
#SPJ4