A piece of equipment costs $75,000 new but depreciates 12% per year in each succeeding year . Find its value after 8 years
Answers
The equipment's value after 8 years, given its original value was $75,000 and it depreciates by 12% each year, is approximately $27,506.62.
To find the value of the equipment after 8 years, we need to calculate its value at the end of each year, taking into account the 12% depreciation per year.
At the end of year 1, the equipment will be worth 88% of its original value
Value at end of year 1 = 0.88 x $75,000 = $66,000
At the end of year 2, the equipment will be worth 88% of its value at the end of year 1
Value at end of year 2 = 0.88 x $66,000 = $58,080
We can continue this process for each year
Value at end of year 3 = 0.88 x $58,080 = $51,206.40
Value at end of year 4 = 0.88 x $51,206.40 = $45,065.91
Value at end of year 5 = 0.88 x $45,065.91 = $39,654.02
Value at end of year 6 = 0.88 x $39,654.02 = $34,991.23
Value at end of year 7 = 0.88 x $34,991.23 = $31,191.80
Value at end of year 8 = 0.88 x $31,191.80 = $27,506.62
Therefore, the value of the equipment after 8 years is $27,506.62.
To know more about depreciating value:
https://brainly.com/question/21212050
#SPJ1
Related Questions
11. Chip has a fruit stand and sells oranges and
grapefruits. In one hour, he sold 30 pieces of fruit
for $7.50. He sold oranges for 20 cents and
grapefruits for 35 cents each. How many of each
kind did he sell?
Answers
Find the lowest common denominator (multiple). Type the equivalent fractions. Then, add or subtract. Simplify your answer. 1
2
1
3
Answers
Answer:what
Step-by-step explanation:what does this mean
what is the probability that a single randomly sampled observation have a value above the mean?
Answers
The probability of a single randomly sampled observation having a value above the mean is approximately 0.1587, assuming a normal distribution.
if the mean of the data is μ and the standard deviation is σ, then the probability of a single observation being above the mean is given by:
P(X > μ) = 1 - P(X ≤ μ)
where X is the random variable representing the data. To calculate this probability, we need to standardize the data by subtracting the mean from each observation and dividing by the standard deviation. This gives us a standard normal variable Z, which has a mean of 0 and a standard deviation of 1.
Then, we can look up the probability in a standard normal table or use a calculator or software to find the area under the standard normal curve to the right of Z = 0.
For example, suppose we have a dataset with a mean of 10 and a standard deviation of 2. If we standardize the data, then a value of 12 would correspond to a Z-score of:
Z = (12 - 10) / 2 = 1
The probability of a value being above the mean is then:
P(X > 10) = 1 - P(X ≤ 10) = 1 - P(Z ≤ 1) = 1 - 0.8413 = 0.1587
Therefore, the probability of a single randomly sampled observation having a value above the mean is approximately 0.1587, assuming a normal distribution.
Learn more about probability
brainly.com/question/30034780
#SPJ11
Can somebody help with this

Answers
Answer:
B
Step-by-step explanation:
Domain is the x value and it is asking your for the coordinates with the same x value.
Besides being simple for its own sake, what other advantage do simple models usually have?
a) Higher accuracy
b) Greater complexity
c) Easier interpretation
d) More detailed predictions
Answers
The correct option is c) Easier interpretation. One of the main advantages of simple models is their ease of interpretation. Simple models tend to have fewer parameters and less complex mathematical equations, making it easier to understand and interpret how the model is making predictions.
This interpretability can be valuable in various domains, such as medicine, finance, or legal systems, where it is important to have transparent and understandable decision-making processes.
Complex models, on the other hand, often involve intricate relationships and numerous parameters, which can make it challenging to comprehend the underlying reasoning behind their predictions. While complex models can sometimes offer higher accuracy or make more detailed predictions, they often sacrifice interpretability in the process.
To know more about complex visit-
brainly.com/question/28235673
#SPJ11
PLEASE HELP I WILL MARK U BRAINLIEST!!!! Solve the equation using the zero-product property. Show your work
(2x + 2)(5x - 5) = 0
Answers
x=-1
5x-5=0
x=1
good luck
a bacteria culture grows with a constant relative growth rate. after 2 hours there are 600 bacteria and after 8 hours the count is 75,000. (a) find the initial population.
Answers
The initial population of the bacteria culture is 200 bacteria.
The initial population of the bacteria culture can be determined using the equation for exponential growth: P(t)=P0(1+rt), where P(t) is the population after time t, P0 is the initial population, and r is the relative growth rate.
In this case, after 2 hours, the population is 600 and after 8 hours the population is 75,000. Plugging in the values, we get P0 = 600/(1+2*r), or P0 = 600/3. Thus, the initial population of the bacteria culture is 600/3 = 200 bacteria.
Exponential growth is a function of time and rate of growth. It is often used to model population growth or decay, such as in this case. The equation for exponential growth states that the population at any time is equal to the initial population multiplied by the rate of growth at each unit of time.
In this case, the rate of growth (r) is constant over the time period, so the population can be determined by putting in the values for P(t) and P0 and solving for r. Then, using the same equation, the initial population (P0) can be determined.
To know more about exponential growth click on below link:
https://brainly.com/question/1340582#
#SPJ11
Give 3 examples of linear equation with two variable.
Show
and explain the computation and make a graph .
300 words
Answers
The two variables, x and y, represent the x- and y-coordinates on the graph, respectively. The graph visually represents the solution set of the equation, showing all possible points that satisfy the equation.
Here are three examples of linear equations with two variables, along with their computations and graphs:
1. Equation: 2x + 3y = 6
Computation: To find the values of y for different x values, we can choose arbitrary values of x and solve for y. For example, when x = 0, we have 2(0) + 3y = 6, which simplifies to 3y = 6, and y = 2. Similarly, when x = 2, we have 2(2) + 3y = 6, which simplifies to 4 + 3y = 6, and y = 2/3.
Graph: The graph will be a straight line passing through the points (0, 2) and (2, 2/3).
2. Equation: -4x + 2y = 8
Computation: Following a similar process, we can find the values of y for different x values. When x = 0, we have -4(0) + 2y = 8, which simplifies to 2y = 8, and y = 4. When x = -2, we have -4(-2) + 2y = 8, which simplifies to 8 + 2y = 8, and y = 0.
Graph: The graph will be a straight line passing through the points (0, 4) and (-2, 0).
3. Equation: x + y = 5
Computation: Similarly, we can find the values of y for different x values. When x = 0, we have 0 + y = 5, and y = 5. When x = 3, we have 3 + y = 5, and y = 2.
Graph: The graph will be a straight line passing through the points (0, 5) and (3, 2).
In each case, the computation involved solving for one variable in terms of the other and substituting different values to obtain corresponding values. The graph of each equation will be a straight line because the relationship between the variables is linear. The two variables, x and y, represent the x- and y-coordinates on the graph, . The graph visually represents the solution set of the equation, showing all possible points that satisfy the equation.
To learn more about graph click here:brainly.com/question/17267403
#SPJ11
To reduce a fraction, divide the numerator and denominator by the ? . Select one:
a. denominator
b. numerator
c. same number
d. smallest fraction
Answers
To reduce a fraction, you divide the numerator and denominator by the same number.
This number is the greatest common divisor (GCD) of the numerator and denominator. By dividing both the numerator and denominator by their GCD, you simplify the fraction to its simplest form. The GCD is the largest number that evenly divides both the numerator and denominator without leaving a remainder.
Dividing by the GCD ensures that the fraction is expressed in its lowest terms, where the numerator and denominator have no common factors other than 1. This process eliminates any common factors and reduces the fraction to its simplest representation.
Therefore, To reduce a fraction, you divide the numerator and denominator by the same number. Option c is correct.
Learn more about Fraction here
https://brainly.com/question/10354322
#SPJ4
r(x) = 2√x s(x) = √x
(rs)(4) = ?
Answers
Answer:
8
Step-by-step explanation:
Answer:
8
Step-by-step explanation:
I got a 100 on edgenu
Please help me !!!!!!

Answers
Answer:
2
Step-by-step explanation:
-2+4=2
pls help asap if you can!!!!!

Answers
Answer:
x = 24
Step-by-step explanation:
if a and b are parallel then
62 and 5x - 2 are same- side interior angles and sum to 180° , that is
5x - 2 + 62 = 180
5x + 60 = 180 ( subtract 60 from both sides )
5x = 120 ( divide both sides by 5 )
x = 24
thus for a to be parallel to b , then x = 24
What is the solution of the inequality
- 47 < -20
Answers
Answer:
True?
Step-by-step explanation:
There not really an equation here.
But that is correct.
-47 is less than -20
If you walk to school at a rate of 3 miles per hour, how long will it take you to walk 6 miles?
Answers
At the ice skating competition, Vonda finished with a total of 44 points. Melinda finished with 0. 2 fewer points than Vonda, and Davina finished with 1. 68 fewer points than Melinda. How many points did Davina have? Help me!!!
Answers
The number of points Davina have in the ice skating competition is 33.52.
Define the term product of the number?As the question stated,
Vonda scored a total of 44 points to finish.Melinda came in second place, 0. 2 points behind Vonda.Melinda finished ahead of Davina with 1. 68 fewer points.Then,
Formulate based on the conditions stated: 44 - 1.68 - (44 x 0.2).
Determine the quotient or product: 44 - 1.68 - 8.8.
Determine the total or difference: 42.32 - 8.8
Determine the total or difference: 33.52.
The, the number of points Davina have is 33.52.
To know more about the product of the number, here
https://brainly.com/question/1654645
#SPJ4
What is the solution?
-4(3) - 3 = ?
Answers
I hope it helps you :)
what is the quotient of 10/16 ÷ 5/16
Answers
Answer: 2
Step-by-step explanation:
Answer:
Step-by-step explanation:
The answer is 2.
(10/16)/(5/16)=2
10/5=2
16/16=1
2/1=2
Qué número sumado igual da 60 que no sea 20
Answers
Answer: 30
Step-by-step explanation:
HELPPPP!!!!!
A rare baseball card just sold for $12,000. Sports experts anticipate this baseball card to increase in value by 9%
each decade.
According to the experts, about how much should the baseball card be worth in 30 years?
Answers
The baseball card be worth in 30 years is: $159212.14
We have the following information available from the question is:
A rare baseball card just sold for $12,000
This baseball card to increase in value by 9%
each decade.
The principal = $12,000
Rate of interest (r) =9%
Time period (t) = 30 years
The number of times per year the interest is compounded (n) = 1
We know the formula is:
\(=P(1+\frac{r}{n} )^n^t\)
Plug all the values, we get:
\(=12000(1+\frac{\frac{9}{100} }{1} )^3^0\)
Then, Evaluate the equation/expression:
=> $159212.14
Learn more about Compound interest at:
https://brainly.com/question/21847227
#SPJ2
how long it will take for an investment of 1000 dollars to double in value if the interest rate is 7.5 percent per year, compounded continuously?
Answers
By using the formula for compound interest, it can be calculated that
It took 0.0924 years to make $1000 to double in value if the interest rate is 7.5 percent per year, compounded continuously
What is compound interest?
If the principal on a certain rate over a certain period of time increases exponentially rather than linearly, the interest earned is called compound interest
If p is the principal, r is the rate and n is the time in year, then amount is calculated by the formula
\(A = p(1+\frac{r}{100})^n\)
The difference between amount and the principal gives the compound interest.
Let the time required be t years
Principal = $1000
Rate = 7.5%
Amount = $2000
\(A = pe^{rt}\\\\2000 = 1000e^{7.5t}\\\\\frac{2000}{1000} = e^{7.5t}\\\\e^{7.5t} = 2\\\\7.5 t = ln2\\\\7.5t = 0.693\\\\t = \frac{0.693}{7.5}\\\\t = 0.0924 \ years\)
To learn more about compound interest, refer to the link-
https://brainly.com/question/24924853
#SPJ4
8) Imani spent half of her weekly allowance
playing mini-golf. To earn more money her
parents let her wash the car for $4. What is
her weekly allowance if she ended with
$12?
how would i solve this in a two step equation? pls and thanks
Answers
Answer:
See below.
Step-by-step explanation:
We can represent Imani's weekly allowance with the variable a. The equation you can write is:
1/2a+4=12
2(1/2a+4)=2(12)
a+8=24
a=16
The Imani's weekly allowance value is $16.
To solve this problem using a two-step equation, follow these steps:
Step 1: Let's represent Imani's weekly allowance with the variable "x."
Step 2: We know that Imani spent half of her allowance playing mini-golf, so the amount she spent is (1/2) × x. Additionally, she earned $4 by washing the car. Therefore, the equation becomes:
x - (1/2) × x + 4 = 12
To solve this equation, we need to combine like terms and isolate the variable "x":
(1/2) ×x = 12 - 4
(1/2) × x = 8
Next multiply both sides of the equation by 2 to eliminate the fraction:
2 × ((1/2) × x) = 2 × 8
x = 16
To know more about value here
https://brainly.com/question/30145972
#SPJ6
Evaluate function expression −2⋅f(−6)−7⋅g(−7)=
Answers

Answer:
11
Step-by-step explanation:
-2 • f(-6) -7 • g(-7) = ?
As per graph:
f(-6) = 5
g(-7) = -3
Calculation:
-2 • f(-6) -7 • g(-7) =
-2(5) - 7(-3) =
-10 + 21 =
11
(x+5)(x+1)+(x+5)(x+8)
Answers
Answer:
2x² + 19x + 45
Step-by-step explanation:
(x + 5)(x + 1) + (x + 5)(x + 8) ← expand both sets of factors using FOIL
= x² + 6x + 5 + x² + 13x + 40 ← collect like terms
= 2x² + 19x + 45
Please answer this by midnight I need it for Algebra 3 and I don't want to fail please

Answers
The length of the arc is about 1.758 cm.
First, we need to determine the size of the angle. If we have pi/5 radians, we can convert that to 36 degrees, because pi radians is 180 degrees. Now, we know the measure of the arc is 36 degrees. 36 degrees out of 360 degrees is 10%.
Our arc is 10% of the circumference of the circle.
The circumference is 2(pi)r or 2(3.14)2.8 = 17.58 cm
Now, multiply 17.58 by 0.1 to get a total of 1.758 cm.
hii please help quickly?
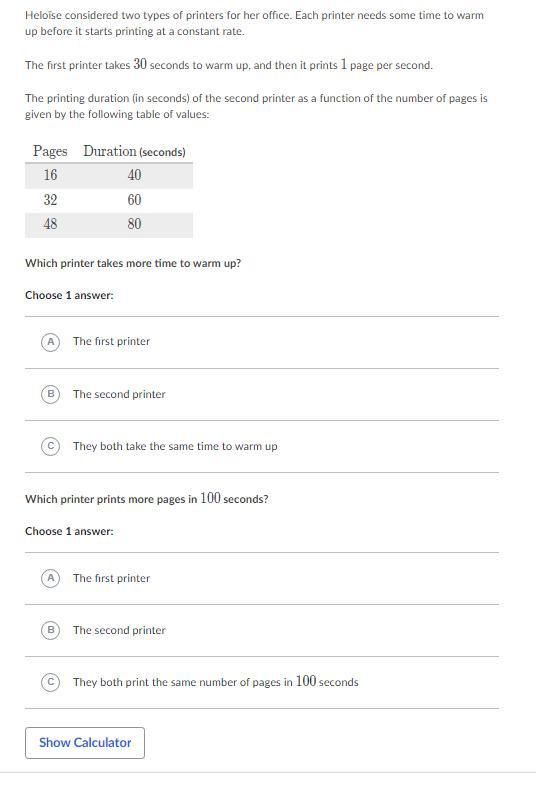
Answers
Problem 1
x = duration in seconds
y = number of pages
The 1st printer has the equation y = x-30 where x > 30.
For example, if x = 31 seconds have elapsed, then y = x-30 = 31-30 = 1 page has been printed. It turns out that the x-intercept will tell us when that 1st page will be printed. The x-intercept for y = x-30 is 30, which means the 31st second is when the first page is printed.
Now let's find the equation for the 2nd printer. The three points on this line are:
(40,16)(60,32)(80,48)Pick two of those points to determine the slope. I'll select the first two points.
m = (y2 - y1)/(x2 - x1)
m = (32-16)/(60-40)
m = 16/20
m = 0.8
Now use point-slope form to do the following steps:
y - y1 = m(x - x1)
y - 16 = 0.8(x - 40)
y - 16 = 0.8x - 32
y = 0.8x - 32 + 16
y = 0.8x - 16
If you were to plug in y = 0 and solve for x, then,
y = 0.8x - 16
0 = 0.8x - 16
16 = 0.8x
0.8x = 16
x = 16/0.8
x = 20
The warm-up time for the 2nd printer is 20 seconds, which is less than the warm-up time for the 1st printer (30 seconds).
Answer: The first printer.========================================================
Problem 2
Plug x = 100 into the 1st equation
y = x-30
y = 100-30
y = 70
The 1st printer can print out 70 pages in 100 seconds.
Repeat for the 2nd equation.
y = 0.8x-16
y = 0.8*100-16
y = 80-16
y = 64
The 2nd printer can print 64 pages in 100 seconds.
So even though the 1st printer needs a longer warm-up time, its rate or speed is faster than the 2nd printer to be able to print more pages.
Answer: The first printer.What is the coefficent of the r-term in -8r+24s-9r-7
Answers
The coefficient of the r-term in -8r+24s-9r-7 is -8 - 9 = -17.
In the given expression -8r+24s-9r-7, the term with the variable r is -8r and the coefficient of the r-term is -8.
A coefficient is a numerical factor that multiplies a variable or variables in a term. In this case, -8 is the coefficient of the term -8r.
The coefficient of a term with a variable indicates how many times the variable appears in that term, multiplied by the sign of the coefficient.
For example, the term -8r means -8 times r, so the coefficient is -8. It is important to identify coefficients when simplifying expressions, solving equations, or manipulating algebraic expressions.
Learn more about:
coefficient : brainly.com/question/1594145
#SPJ11
Find the Surface area of the trapezoid
please help
show work

Answers
Answer:
259.5
Step-by-step explanation:
8.1*12=97.2
Area of trapiezium = 1/2(b+a)h
(2.8+8.1)=10.9
10.9*3/2=16.35
16.35*2=32.7
2.8*12=33.6
33.6+32.7+97.2=163.5
4*12*2=96
163.5+96=259.5
What is the volume of a cylinder that has the same base area and the same height?

Answers
Answer:
108 cubic units
Step-by-step explanation:
Volume of cone = 36\(\pi\) cubic units
⇒ 1/3 π r² h = 36 π
⇒ πr²h = 36π × 3
⇒ πr²h = 108 π
The cylinder has the same base area and the same height as the cone.
Volume of cylinder = πr²h
= 108 π cubic units
Volume of cylinder = 108 cubic units
2/-3 divided by -1 2/7 =
pls explain the answer
Answers
Answer:
\(\frac{14}{27}\)
Step-by-step explanation:
\(-1\frac{2}{7} = -\frac{9}{7}\) Plug -9/7 in: \(-\frac{2}{3}\) ÷ \(-\frac{9}{7}\) -2/3 ÷ -9/7 = 2/3 ÷ 9/7 = 2/3 × 7/9\(\frac{2}{3}\) × \(\frac{7}{9} = \frac{14}{27}\)I hope this helps!
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
\( \frac{2}{ - 3} \div (- 1 \frac{2}{7}) = \\ \)
\( - \frac{2}{3} \div ( - \frac{ 7}{7} - \frac{2}{7} ) = \\ \)
\( - \frac{2}{3} \div ( \frac{ - 7 - 2}{7} ) = \\ \)
\( - \frac{2}{3} \div ( - \frac{9}{7} ) = \\ \)
Negatives simplifies
\( \frac{2}{3} \div \frac{9}{7} = \\ \)
\( \frac{2}{3} \times \frac{7}{9} = \\ \)
\( \frac{14}{27} \\ \)
Done...
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
The area of a rectangular fence is 500 square feet. If the width of the
fence is 20 feet, then find its length.
Answers
Answer
Here the area and the width of the rectangular fence are given. We have to find length of the fence.
( diagram )
The area A of a rectangle is given by the formula A=lw where l is the length and w is the width.
Given that area is 500 square feet and width is 20 feet.
Substituting values in formula,
⇒500=l×20
⇒20/500
= 20/1×20
[ Dividing both sides by 20 ]
⇒l=25 feet
∴ length of rectangular fence is 25 feet.
Hence, the answer is 25.
