Answer to Image .PleasePleasePleasePleasePleasePleasePleasePleasePleasePleasePlease

Answers
Answer:
ASA congruence postulate
Step-by-step explanation:
The previous steps show the angles at either end of segment RT are congruent with their corresponding angles. This means you have congruent angles, congruent sides, and congruent angles, in that order. The ASA congruence postulate is all that is needed for you to complete the proof.
Answer:
ASA congruence postulate
Step-by-step explanation:
Related Questions
Shamin Jewelers sells diamond necklaces for $442 less 10%. Jewelers offers the same necklace for $527 less 34%, 14% What additional rate of discount must offer to meet the competitor's price
Answers
Answer:
The selling price of the diamond necklace at Shamin Jewelers after 10% discount is:
$442 * 0.9 = $397.80
The selling price of the same necklace at the competitor's store after 34% and 14% discount is:
$527 * 0.66 * 0.86 = $247.08
So, Shamin Jewelers needs to offer an additional discount to meet the competitor's price:
$397.80 - $247.08 = $150.72
To calculate the additional rate of discount, we divide the difference by the original selling price at Shamin Jewelers and multiply by 100:
($150.72 / $442) * 100 = 34.11%
Therefore, Shamin Jewelers must offer an additional 34.11% discount to meet the competitor's price.
Step-by-step explanation:
Find the absolute value of 16
Answers
Answer:
16
Step-by-step explanation:
Absolute value always means positive i.e to remove any negative signs in front of a number.
Since 16 is a simple digit with the as the positive sign is invincible.
So, the absolute value of 16 is 16.
\(\huge\boxed{\maltese{\sf{Hi~there!}}}\)
Let's talk about what the absolute value is.
Notation: | |
\(\maltese\) The absolute value of a number is always positive, even if the number is negative.
Thus, the absolute value of 16 is 16. :)
\(\huge\boxed{\star{Answer:16\star}}}\)
Hope it helps! Enjoy your day!
~Just a determined gal
\(\bf{S^il^en^t\)
You can use these steps to work out the amount of income tax you pay each month.
Work out
monthly salary - 987.5
Work out
answer to Step 1 +5
Step 1
Step 2
Cho has a salary of £24 000 per year.
Helen has a salary of £1720 per month.
How much more income tax does Cho pay than Helen each month?
Answers
The amount more in income tax that Cho pays than Helen each month would be £56.
How to find the income tax ?First, find Helen's yearly salary :
= 1, 720 x 12
= £ 20, 640
Both Cho's and Helen's annual salaries fall within the Basic rate tax bracket.
Cho 's monthly tax would be:
= (( 24, 000 - 12, 570 ) x 20 % ) / 12
= £ 190. 50
Helen's monthly tax :
= (( 20, 640 - 12, 570 ) x 20 % ) / 12
= £ 134.50
The difference is therefore :
= 190. 50 - 134.50
= £56
Find out more on income tax at https://brainly.com/question/20704728
#SPJ1
Find the solution of the system for which

Answers
Answer:
3,0,-6,0
Step-by-step explanation:
x1=3 because 3+0+0=3
since x2 and s2=0.
1. Find the equation of the image of the circle x² + y2 + 16x-24y + 183 = 0 by rotated the line mirror 4x + 7y + 13 = 0. 2. The image of the circle (x - 3)² + (y-2)² = 1 in the line mirror ax + by = 19 is (x-1)³ + (y-16)2 = 1 then, find the values of (a, b). 3. Find the equation of a line passing through the origin and making an angle with the 4 line y-3x-5. 4. A parabola is drawn with its focus at (3,4) and vertex at the focus of the parabola y²-12x - 4y + 4 = 0. The n find equation of the parabola. 5. If the line ax + by + c = 0 touches the circle x² + y² - 2x = and is normal to the circle x² + y² + 2x - 4y + 1 = 0, then find the value of (a, b). 6. If the line through the points (-2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x. -3 7.1² 14 231= [] then find the matrix A 8. Find the equation of the ellipse having its center at the point (2,-3), one and one vertex at (4, -3). 3 9. Find the value of x if-1 0 10. Solve the linear system using Cramer's rule a) 2 1 2 4 (6x - 4y = -12 8x - 3y = -2 X = 16 -21 3x + 2y = z = 5 b) x-y+3z = -15 (2x + y +7z = -28 one focus at (3,-3) 11. Find the value of k for which the following system of linear equations has infinite solutions: x + (k+1)y = 5 ((k+1)x + 9y = 8k - 1
Answers
Answer:
-72x - 53y + 287 = 0.
Step-by-step explanation:
To find the equation of the image of the circle, we need to reflect each point on the circle in the given line mirror.
The line mirror equation is given as 4x + 7y + 13 = 0.
The reflection of a point (x, y) in the line mirror can be found using the formula:
x' = (x - 2Ay - 2B(Ax + By + C)) / (A^2 + B^2)
y' = (y - 2Bx + 2A(Ax + By + C)) / (A^2 + B^2)
where A, B, and C are the coefficients of the line mirror equation.
For the given line mirror equation 4x + 7y + 13 = 0, we have A = 4, B = 7, and C = 13.
Now, let's find the equations of the image of the circle.
The original circle equation is x² + y² + 16x - 24y + 183 = 0.
Using the reflection formulas, we substitute the values of x and y in the circle equation to find x' and y':
x' = (x - 2Ay - 2B(Ax + By + C)) / (A^2 + B^2)
= (x - 2(4)y - 2(7)(4x + 7y + 13)) / (4^2 + 7^2)
= (x - 8y - 8(4x + 7y + 13)) / 65
= (x - 8y - 32x - 56y - 104) / 65
= (-31x - 64y - 104) / 65
y' = (y - 2Bx + 2A(Ax + By + C)) / (A^2 + B^2)
= (y - 2(7)x + 2(4)(Ax + By + C)) / (4^2 + 7^2)
= (y - 14x + 8(Ax + By + C)) / 65
= (y - 14x + 8(4x + 7y + 13)) / 65
= (57x + 35y + 104) / 65
Therefore, the equation of the image of the circle is:
(-31x - 64y - 104) / 65 + (-57x + 35y + 104) / 65 + 16x - 24y + 183 = 0
Simplifying the equation, we get:
-31x - 64y - 57x + 35y + 16x - 24y + 183 + 104 = 0
-72x - 53y + 287 = 0
So, the equation of the image of the circle is -72x - 53y + 287 = 0.
in order to model the -3.5 - (2.7) on a number line you start from and move units
Answers
In order to model the expression -3.5 - (2.7) on a number line;
place the cursor on -3.5 and move towards the left by 2.7 as shown in the diagram below;We have to move to the left since -2.7 is a negative valueThe number line is a line containing negative values to the left of the number line and positive values to the right of the number lines.
In order to model the expression -3.5 - (2.7) on a number line;
place the cursor on -3.5 and move towards the left by 2.7 as shown in the diagram below;We have to move to the left since -2.7 is a negative valueLearn more here; https://brainly.com/question/23379455

One number is 8 more than another number, and their sum is 16. What are the 2 numbers?
Answers
Answer:
x = 12
y = 4
Step-by-step explanation:
x + y = 16
x - y = 8
y + 8 = x
Replace x with y + 8 in the new equation
8 + 2y = 16 ----> we can minus 8 on both sides
2y = 8 -----> divide both sides by 2
y = 4
Now for the x value
x + 4 = 16 ----> minus 4 on both sides
x = 12
Answer:
12 and 4
Step-by-step explanation:
The ratio of qualified teachers to unqualified teachers is 1;2. Use the given ratio and determine how many qualified teachers there are if there are 540 unqualified teachers. show your calculations
Answers
Answer:
270
Step-by-step explanation:
by using the proportion rule:
let X be the number of qualified teachers then
1:2=X=540 i.e.
1/2 = X/540
by cross multiplication,
540x1=2xX
540=2X i.e.
X=540/2
X=270
There are 270 qualified teachers.
To solve this, we would apply the knowledge of proportion.
It is simply a way of stating that two ratios are of equal measure.
For example, \(a:b = x:y\) or \(\frac{a}{b} = \frac{x}{y}\)
Applying the following proportion rule given that:
Ratio of qualified teachers to unqualified teachers is 1:2.
Number of unqualified teachers = 540
Let number of qualified teachers be represented by x.
Therefore:
\(\frac{1}{2} = \frac{x}{540}\)
Cross multiply
\(2x = 540(1)\)
Divide both sides by 2
\(\frac{2x}{2} = \frac{540}{2} \\x = 270\)
Therefore, the number of qualified teachers is 270.
Learn more about ratio here:
https://brainly.com/question/21768124
Select the correct answer.
Which expression is equivalent to the given expression?
(7y^6) (2y^-4)²

Answers
Answer:
c
Step-by-step explanation:
\((7 {y}^{6} ) {(2 {y}^{ - 4} )}^{2 } = = = > \\ (7 {y}^{6} )( \frac{4}{ {y}^{8} } ) = = = > \\ ( \frac{28 {y}^{6} }{ {y}^{8} } ) = = > \\ ( \frac{28}{ {y}^{2} } )\)
Assume that the situation can be expressed as a linear cost function. Find the cost function in this case.
Marginal cost: $15; 150 items cost $5500 to produce.
The linear cost function is C(x) =
Answers
The linear cost function is C(x) = 15x + 3250 and the cost function in marginal cost: $15; 150 items cost $5500 to produce is $ 5500 .
The linear operate is expressed as y = mx + b .....(1)A linear value operate expresses value as a linear operate of the amount of items;Let C(x) is that the total value, and x is that the range of things.
The slope "m" is named the cost and "b" is named the charge.
The value of m is $15 and the price of "x" is 150.
Total cost of 150 items are $5500
Substitute all the values within the equation (1) , we get
5500 = 15 (150) + b
5500 = 2250 + b
3250 = b
Hence , linear cost function is given by C(x) = 15x + 3250
Learn more about linear cost function here :
https://brainly.com/question/4025726
#SPJ9
PLEASE HURRY DUE TODAY WILL MARK BRAINLESTIS RIGHT
what is √29 Place a dot on the number line at the BEST approximation

Answers
Answer:
5.4
Step-by-step explanation:
square of 29 = 5.385164807
5.385164807 estimated is 5.4

3. If triangle ABC was reflected across the y-axis, what would be the coordinates of C'?
(4,1)
(-4,-4)
(1,1)
(-4,-1)

Answers
Answer:
(4,1)
Step-by-step explanation:
(4,1) is the answer
3 by 5 ratio 8 by 9
Answers
Answer:
5:24
Step-by-step explanation:
Given data
3 by 5
=3*5
=15
8 by 9
=8*9
=72
Hence the ratio is
15:72
Equivalent to
5:24
4) Students in Ms. Udon
science class planted 13
conifers in different places
around the school yard. They
measured the heights (in inches)
of the conifers one month after
planting them. How many
conifers are greater than 6 1/4
inches tall but less than 8 1/2
inches tall?
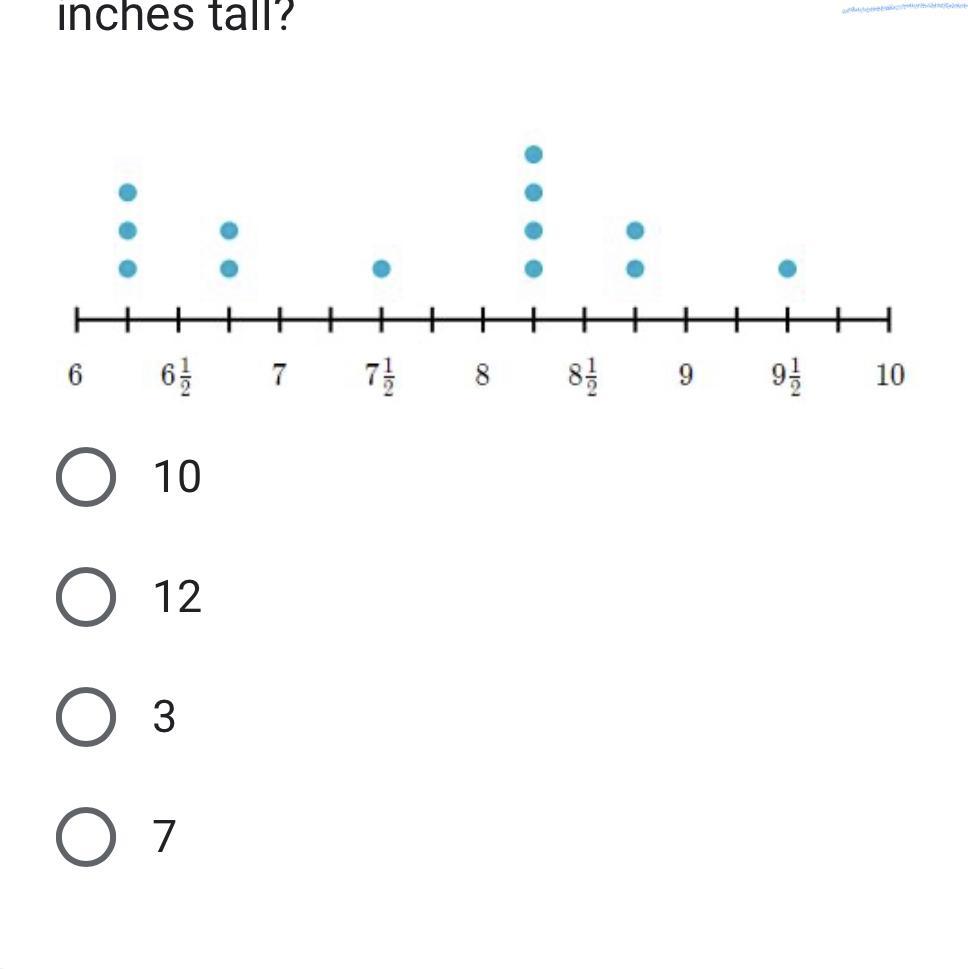
Answers
Considering the dot plot, the tallest conifer is 3.25 inches taller than the shortest conifer.
This shows, with dots, the number of times that each of the measures appears in a data set.
For finding the dot plot, we have that:
The shortest conifer measures 6 and 1/4
= 6.25 inches.
The tallest conifer measures 9.5 inches.
The difference is:
9.5 - 6.25 = 3.25 inches.
Therefore the tallest conifer is 3.25 inches taller than the shortest conifer.
More can be learned about a dot plot at;
brainly.com/question/24912483
#SPJ1
Question 9/30 If ADD = 81, BAD = 49, and CAD = 64. then what is the value of ADA?
Answers
The value of ADA is 36
The question could be approached as a quantitative reasoning exercise :
Assigning each alphabet a numeric value corresponding to its position in the English alphabet :
A has a value of 1
B has a value of 2
C has a value of 3
D has a value of 4
ADD could be interpreted as :
ADD = (1 + 4 + 4) = 9
Taking the square of the sum ; 9² = 81
ADD = 81
BAD could be interpreted as :
BAD = (2 + 1 + 4) = 7
Taking the square of the sum ; 7² = 49
CAD could be interpreted as :
CAD = 3 + 1 + 4 = 8
Taking the square of the sum ; 8² = 64
Therefore ;
ADA could be interpreted as :
ADA = 1 + 4 + 1 = 6
Square of the sum ; 6² = 36
Hence, the value of ADA is 36
Learn more : https://brainly.com/question/18109354
At the beginning of year 1, Paolo invests $500 at an annual compound
interest rate of 4%. He makes no deposits to or withdrawals from the
account.
Which explicit formula can be used to find the account's balance at the
beginning of year 5? What is the balance?

Answers
Answer:
see below
Step-by-step explanation:
The way the problem is worded, we expect "n" to represent the year number we're at the beginning of. That is the initial balance is that when n=1, and the balance at the beginning of year 5 (after interest accrues for 4 years) is the value of obtained when n=5.
After compounding interest for 4 years, the balance will be ...
500·1.04^4 = 584.93
The matching answer choice is shown below.

Answer:
b
Step-by-step explanation:
It is known that 4 WHOEVER ANSWERS CORRECTLY WILL BE MARKED BRAINLIEST
Answers
Answer:
jsjsjsjs
Step-by-step explanation:
sjsjsjsjdjdjdjdjdjjdjdfjjfdjjdjdjdjdjdjdjdjd
\(\lim_{t\to 0} \det\left(\begin{bmatrix} \displaystyle \int_0^t \frac{u}{\sinh(u)} du & \cos(t) & \displaystyle \sum_{n=1}^{\infty} \frac{1}{n+t+i} \\ \displaystyle \frac{d}{dt} \left(e^t \ln \left(\frac{1}{t}\right) \right) & \binom{5}{2} t^2 & \displaystyle \prod_{n=1}^4 \left(\sqrt{1+nt} - 1\right) \\ i\binom{5}{3} t^3 \sin(2t) & \displaystyle \sum_{n=1}^{5} n^2 e^{int} & \binom{8}{2} t^2 + i\binom{5}{2} t^3 \cos(3t) \end{bmatrix}\right)\)
Answers
The limit of the determinant as \(t\) approaches 0 is \(-\infty\).
To evaluate this limit, we can use the fact that the determinant is a linear function of each row, and that the limit of a sum is the sum of the limits. Therefore, we can compute the limit of each row separately.
Starting with the first row, we have:
\(\lim_{t\to 0} \int_0^t \frac{u}{\sinh(u)} du
= \lim_{t\to 0} \frac{\int_0^t \frac{u}{\sinh(u)} du}{t} \cdot t
= \lim_{t\to 0} \frac{\frac{t}{\sinh(t)} - 1}{t} \cdot t
= \lim_{t\to 0} \frac{1-\sinh(t)}{t\sinh(t)} = 1\)
\(\lim_{t\to 0} \cos(t)
= 1\)
\(\lim_{t\to 0} \sum_{n=1}^{\infty} \frac{1}{n+t+i}
= \sum_{n=1}^{\infty} \lim_{t\to 0} \frac{1}{n+t+i}
= \sum_{n=1}^{\infty} \frac{1}{n+i}
= \psi(i+1) \approx 0.643 + 0.41i\)
where \(\psi(z)\) is the digamma function.
Therefore, the limit of the first row is \(1 \cdot 1 \cdot \psi(i+1) = \psi(i+1)\).
Moving on to the second row, we have:
\(\lim_{t\to 0} \frac{d}{dt} \left(e^t \ln \left(\frac{1}{t}\right) \right)
= \lim_{t\to 0} \frac{e^t}{t} - \lim_{t\to 0} \frac{e^t}{t^2}
= 1 - \infty = -\infty\)
\(\lim_{t\to 0} \binom{5}{2} t^2
= 0\)
\(\lim_{t\to 0} \prod_{n=1}^4 \left(\sqrt{1+nt} - 1\right)
= \prod_{n=1}^4 \lim_{t\to 0} \left(\sqrt{1+nt} - 1\right)
= \prod_{n=1}^4 \sqrt{1+n} - 1
= 4\sqrt{2} - 5\)
Therefore, the limit of the second row is \(-\infty \cdot 0 \cdot (4\sqrt{2} - 5) = 0\).
Finally, for the third row, we have:
\(\lim_{t\to 0} i\binom{5}{3} t^3 \sin(2t) = 0\)
\(\lim_{t\to 0} \sum_{n=1}^{5} n^2 e^{int}
= \sum_{n=1}^{5} n^2 \lim_{t\to 0} e^{int}
= \sum_{n=1}^{5} n^2
= 55\)
\(\lim_{t\to 0} \binom{8}{2} t^2 + i\binom{5}{2} t^3 \cos(3t) = 28\)
Therefore, the limit of the third row is \(0 \cdot 55 \cdot 28 = 0\).
Putting everything together, we get:
\(\lim_{t\to 0} \det\left(\begin{bmatrix} \displaystyle \int_0^t \frac{u}{\sinh(u)} du & \cos(t) & \displaystyle \sum_{n=1}^{\infty} \frac{1}{n+t+i} \\ \displaystyle \frac{d}{dt} \left(e^t \ln \left(\frac{1}{t}\right) \right)
& \binom{5}{2} t^2 & \displaystyle \prod_{n=1}^4 \left(\sqrt{1+nt} - 1\right) \\ i\binom{5}{3} t^3 \sin(2t) & \displaystyle \sum_{n=1}^{5} n^2 e^{int} & \binom{8}{2} t^2 + i\binom{5}{2} t^3 \cos(3t) \end{bmatrix}\right) = \det\left(\begin{bmatrix} \psi(i+1) & 1 & 0 \\ -\infty & 0 & 4\sqrt{2}-5 \\ 0 & 55 & 28 \end{bmatrix}\right) = -\infty\)
To learn more about : determinant
https://brainly.com/question/24254106
#SPJ11
simplify 22 - (-24) + (-32)
Answers
Simplify
22 - (-24)
Swap since they are both negatives.
22-(-24) =
22+(24)
22+24
= 46
Which now add in the negative 32 to the problem
46 + (-32)
Recreate the problem to make it more simple:
46 - 32
= 14
The population of a city decreases by 0.9% per year. If this year's population is 338,000, what will next year's population be, to the nearest individual?
Answers
Answer:
The population will be 334,958.
Step-by-step explanation:
Multiply 338,000 by 0.009 to get the answer. The reason is to multiply by a percentage, you move the decimal two spots to the left. For example, 0.9 -> 0.009. Another would be 3 -> 0.03.
The time between surface finish problems in a galvanizing process is exponentially distributed with a mean of 41 hours. A single plant operates three galvanizing lines that are assumed to operate independently. Round your answers to four decimal places (e.g. 98.7654).
(a) What is the probability that none of the lines experiences a surface finish problem in 41 hours of operation?
(b) What is the probability that all three lines experience a surface finish problem between 24 and 41 hours of operation?
Answers
Answer:
a) The probability that none of the lines experiences a surface finish problem in 41 hours of operation is 0.0498.
b)The probability that all three lines experience a surface finish problem between 24 and 41 hours of operation is 0.0346.
Step-by-step explanation:
\(Mean = \frac{1}{\lambda} = 41\\P(X\leq x)= 1-e^{-\lambda x}\)
\(P(X>x)= e^{-\lambda x}\)
a)
\(P(x> 41, y>41, Z>41) = (P(X>41))^{3}\\\\P(X>41)=e^{^{-\frac{41}{41}}}=e^{-1}\)
\(P(x> 41, y>41, Z>41) = \left (e^{-1} \right )^{3}\\\\P(x> 41, y>41, Z>41) = e^{-3} = 0.0498.\)
b)
\(\lambda =\frac{24}{41}\\P(X=1)=e^{-\lambda }\cdot \lambda =\left ( e^{-0.585} \right )\left ( 0.585 \right )\\P(X=1)=0.326\)
For 3 where, P(X=1, Y==1, Z=1)
\(= (0.326)^{3} \\\\= 0.0346\)
please please help last text then finals l give brainliest

Answers
1. The x - intercepts of the parabola are
x = 2.5 s and x = 7.5 s2. The meaning of the x-intercepts are the plane takes of at x = 2.5 s and lands at x = 7.5 s
3. The vertex of the parabola is at (5, 80).
What is a parabola?A parabola is a curved shape
1. Given the parabola above, to find the x - intercepts, we proceed as follows.
The x-intercepts are the points at which the graph cuts the x-axis.
They are
x = 2.5 s and x = 7.5 s2. The meaning of the x-intercepts in this problem are the points where the plane takes off and lands on the ground.
The plane takes of at x = 2.5 s and lands at x = 7.5 s
3. The vertex is the maximum point on the graph.
So, we see that the vertex is at x = 5 s and y = 80 ft
So, the vertex is at (5, 80).
Learn more about parabola here:
https://brainly.com/question/28094027
#SPJ1
Which of the following mathematical patterns is evident in the piece below?
Answers
Consider that, of all the given options, the right side of the picture seems identical to the left side of the picture.
But it cannot be identical, since the letter on the right side "FIDES" cannot be seen on the right side of the picture.
Rest of all the designs seem symmetrical about the middle vertical line.
Since it is not perfectly identical, not perfectly symmetric, it can be referred as SIMILAR.
So similar patterns are evident in the given piece.
Therefore, option C is the most suitable choice.
what are the assymptotes of this equation
Answers
determine which number or numbers can be a solution for the inequality
32+a>44 11, 12, 13, 14
Answers
The numbers can be a solution for the inequality 32+a>44 is 13 and 14.
What is the solution set to an inequality or an equation?If the equation or inequality have variable terms, than there might be some values of those variables for which the equation or inequality might be correct. Such values are known as solution to that equation or inequality. To set of such values are called solution set to be considered equation or inequality.
Given that;
The inequality= 32+a>44
To solve the inequality 32 + a > 44, we need to isolate the variable "a" on one side of the inequality.
32 + a > 44
Subtract 32 from both sides:
a > 44 - 32
a > 12
This means that any number greater than 12 can be a solution to the inequality.
Therefore, the inequalities numbers 13 and 14 can be solutions, but 11 and 12 cannot.
To learn more about inequalities visit:
https://brainly.com/question/27425770
#SPJ9
what is inequalities
Answers
Inequalities are used in various branches of mathematics, as well as in real-world applications such as economics, physics, and social sciences, to describe relationships, make comparisons, and analyze data.
Inequalities are mathematical statements that describe a relationship between two values or expressions, indicating that one is greater than, less than, or not equal to the other. Inequalities are used to compare quantities and express their relative sizes or order.
The most common symbols used in inequalities are:
">" (greater than): indicates that the value on the left side is larger than the value on the right side.
"<" (less than): indicates that the value on the left side is smaller than the value on the right side.
"≥" (greater than or equal to): indicates that the value on the left side is greater than or equal to the value on the right side.
"≤" (less than or equal to): indicates that the value on the left side is less than or equal to the value on the right side.
"≠" (not equal to): indicates that the values on both sides are not equal.
Inequalities can be represented using variables, constants, and mathematical operations such as addition, subtraction, multiplication, and division. Solutions to inequalities are often expressed as intervals or sets of values that satisfy the given inequality.
Inequalities are used in various branches of mathematics, as well as in real-world applications such as economics, physics, and social sciences, to describe relationships, make comparisons, and analyze data.
For more questions on inequalities
https://brainly.com/question/25275758
#SPJ8
Find the area of the figure. Round your answer to the nearest hundredth.
ill award you brainliest if you actually do it

Answers
Answer:
I think it's about 3840 in.^2
Step-by-step explanation:
The shape is a half circle and a parallelogram
Area of a half circle is 1/2 x pi x r ^2
R is half the diameter(8in), r = 4
Area of half circle = 1/2 x 3.14 x 4^2
Area of half circle = 25.12 square in.
Area of parallelogram = length x height
Area of parallelogram = 10 x 6 = 60 square in.
Total area = 25.12 + 60 = 85.12 square inches
Answer: 85.12 square inches
Find the original slope of (-6,-1) and (0,3)
Answers
Answer:
slope (m) = 2/3
Step-by-step explanation:
slope = change in x /change in y
Also, slope is y2 - y1 / x2 -x1. That is what I apply for this activity, hence:
slope = 3 - (-1) / 0 - (-6)
= 3 + 1 / 0 + 6
= 4 / 6
= 2/3
∴ slope(m) = 2/3
unit 8 right triangles and trigonometry homework 3 similar right triangles and geometric mean

Answers
The right triangles that have an altitude which forms two right triangles
are similar to the two right triangles formed.
Responses:
1. ΔLJK ~ ΔKJM
ΔLJK ~ ΔLKM
ΔKJM ~ ΔLKM
2. ΔYWZ ~ ΔZWX
ΔYWZ ~ ΔYZW
ΔZWX ~ ΔYZW
3. x = 4.8
4. x ≈ 14.48
5. x ≈ 11.37
6. G.M. = 12·√3
7. G.M. = 6·√5
What condition guarantees the similarity of the right triangles?1. ∠LMK = 90° given
∠JMK + ∠LMK = 180° linear pair angles
∠JMK = 180° - 90° = 90°
∠JKL ≅ ∠JMK All 90° angles are congruent
∠LJK ≅ ∠LJK reflexive property
ΔLJK is similar to ΔKJM by Angle–Angle, AA, similarity postulate∠JLK ≅ ∠JLK by reflexive property
ΔLJK is similar to ΔLKM by AA similarityBy the property of equality for triangles that have equal interior angles, we have;
ΔKJM ~ ΔLKM2. ∠YWZ ≅ ∠YWZ by reflexive property
∠WXZ ≅ ∠YZW all 90° angle are congruent
ΔYWZ is similar to ΔZWX, by AA similarity postulate∠XYZ ≅ ∠WYZ by reflexive property
∠YXZ ≅ ∠YZW all 90° are congruent
ΔYWZ is similar to ΔYZW by AA similarity postulateTherefore;
ΔZWX ~ ΔYZW3. The ratio of corresponding sides in similar triangles are equal
From the similar triangles, we have;
\(\dfrac{8}{10} = \mathbf{ \dfrac{x}{6}}\)
8 × 6 = 10 × x
48 = 10·x
\(x = \dfrac{48}{10} = \underline{4.8}\)3. From the similar triangles, we have;
\(\mathbf{\dfrac{20}{29}} = \dfrac{x}{21}\)
20 × 21 = x × 29
420 = 29·x
\(x = \dfrac{420}{29 } \approx \underline{14.48}\)4. From the similar triangles, we have;
\(\mathbf{\dfrac{20}{52}} = \dfrac{x}{48}\)
20 × 48 = 52 × x
\(x = \dfrac{20 \times 48}{52} = \dfrac{240}{13} \approx \underline{18.46}\)5. From the similar triangles, we have;
\(\mathbf{\dfrac{13.2}{26}} = \dfrac{x}{22.4}\)
13.2 × 22.4 = 26 × x
\(x = \dfrac{13.2 \times 22.4}{26} \approx \underline{ 11.37}\)6. The geometric mean, G.M. is given by the formula;
\(G.M. = \mathbf{\sqrt[n]{x_1 \times x_2 \times x_3 ... x_n}}\)
The geometric mean of 16 and 27 is therefore;
\(G.M. = \sqrt[2]{16 \times 27} = \sqrt[2]{432} = \sqrt[2]{144 \times 3} = \mathbf{12 \cdot \sqrt{3}}\)The geometric mean of 16 and 27 is 12·√37. The geometric mean of 5 and 36 is found as follows;
\(G.M. = \sqrt[2]{5 \times 36} = \sqrt[2]{180} = \sqrt[2]{36 \times 5} = \mathbf{ 6 \cdot \sqrt{5}}\)
The geometric mean of 5 and 36 is 6·√5Learn more about the AA similarity postulate and geometric mean here:
https://brainly.com/question/12002948
https://brainly.com/question/12457640


Which represents the solution(s) of this system of equations?
(4, 4)
(–4, –12)
(4, 4) and (–4, 12)
(–4, 4) and (4, 12)
Answers
The solution to the given system of equation is (4, 4)
Factorizing quadratic functionsFrom the solved steps, the final quadratic functions is given as;
x^2 - 8x + 16 = 0
Factorize to have;
x^2 - 4x - 4x + 16 = 0
x(x-4)-4(x-4) = 0
(x-4)(x-4) = 0
x = 4 and 4
Hence the solution to the given system of equation is (4, 4)
Learn more on system of equation here: https://brainly.com/question/847634
#SPJ1
