Area of this shape irregular polygon the high is 4 and width 13
:)
Answers
The area of this irregular polygon is 344.5 square units.
To find the area of an irregular polygon, you can divide it into smaller, simpler shapes.
In this case, we can divide the polygon into a rectangle and a right triangle.
The rectangle has a height of 4 and a width of 13, so its area is 4 x 13 = 52 square units.
The right triangle has a base of 13 and a height of (110 - 4 x 13) / 2 = 45, since the total height of the polygon is 110.
Therefore, the area of the right triangle is (1/2) x base x height = (1/2) x 13 x 45 = 292.5 square units.
Adding the areas of the rectangle and the triangle, we get a total area of 52 + 292.5 = 344.5 square units.
Learn more about polygon at
https://brainly.com/question/24464711
#SPJ11
Related Questions
10. For which of the following utility functions will there always be only a corner solution? a. U(X,Y)=min(X,3Y) b. U(X,Y)=X
2
+Y
2
c. U(X,Y)=X
2
Y
2
d. U(X,Y)=5X+2Y c. None of the above
Answers
The utility function for which there will always be only a corner solution is option a, U(X,Y) = min(X, 3Y).
A corner solution occurs when the optimal choice lies on the boundary of the feasible region rather than in the interior. In option a, U(X,Y) = min(X, 3Y), the utility function takes the minimum value between X and 3Y. This implies that the utility depends on the smaller of the two variables. As a result, the optimal choice will always occur at one of the corners of the feasible region, where either X or Y equals zero.
For the remaining options, b, c, and d, the utility functions are not restricted to the minimum or maximum values of X and Y. In option b, U(X,Y) = X^2 + Y^2, the utility is determined by the sum of the squares of X and Y. Similarly, in option c, U(X,Y) = X^2Y^2, the utility is a function of both X and Y squared. In option d, U(X,Y) = 5X + 2Y, the utility is a linear combination of X and Y. These functions allow for non-zero values of X and Y to be chosen as the optimal solution, resulting in solutions that do not necessarily lie at the corners of the feasible region. Therefore, option a is the only one that guarantees a corner solution.
Learn more about corner solutionhere:
https://brainly.com/question/30897306
#SPJ11
Landon Wallin is an auto mechanic who wishes to start his own business. He will need $4,500 to purchase tools and equipment. Landon decides to finance the purchase with a 4 year fixed installment loan with an interest rate of 5.5%. Determine Landon's monthly payment. (Use loans formula) How much total money does he pay back the bank in 4 years? Find the interest paid.
Answers
Given
$4,500 to purchase tools
4 year fixed
5.5%
First, converting R percent to r a decimal
r = R/100 = 5.5%/100 = 0.055 per year.
Solving our equation:
A = 4500(1 + (0.055 × 4)) = 5490
A = $5,490.00
Answer:
A = $5,490.00
I = A - P = $990.00
A. Monthly Payment
A/(4*12) = 5490/48 = $114.375
B. Total pay
A = $5,490.00
C. Interest
I = A - P = $990.00
What is the length of a line segment that connects the points located at coordinates (12,-22) and (8,-30)? Do not round answer. (leave as a square root)
Answers
Step-by-step explanation:
\(\text{The length between 2 points, } (x_1, y_1)\text{ and }(x_2,y_2)\text{ is determined by, }\)
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
\(\text{The length between } (12, -22)\text{ and }(8, -30)\text{ is determined by, }\)
\(d=\sqrt{(8-12)^2+(-30-(-22))^2}=\sqrt{4^2+8^2}=\sqrt{4^2(1+2^2)}=4\sqrt5\)
2.248 divided by 5.62
Answers
Answer:
0.4
Step-by-step explanation:
Answer:
44.128114
Step-by-step explanation:
ms. chang tracked the number of homework assignments her two math classes submitted each day. these box plots show the results. which class has a higher median number of submitted homework assignments?
Answers
Answer: Class 2
Step-by-step explanation:Because the median point is higher than class 1
From the boxplot of homework assignments data, the median number of submitted homework assignments by math class 2 to the Ms. chang is higher
A box with whisker plot also called a box plot, it is a graphical way of displaying the distribution of data based on a five number summary. The five numbers summary includes minimum, first quartile [Q1], median, third quartile [Q3] and maximum.
The vertical line that split the box in two is called the median value of data.We have two box plots present in attached figure. Ms. chang tracked the submitted assignment by her class through the box plots. Here orange and blue box plots show the data of number homework assignments of her maths class 1 and class 2 submitted each day respectively. Now, see the box plot and use above discussed definition of median, we conclude that median number of class 1 = 25
Median number of class 2 = 26 > 25.
Hence, class 2 has a higher median number than class 1.
For more information about boxplot, visit :
https://brainly.com/question/14277132
#SPJ4
Complete question:
The attached figure complete the question.


What is the median of the data set?
42, 78, 42, 53, 60
Answers
Answer:
53
Step-by-step explanation:
first put it in least to greatest
42,42,53,60,78
the middle value is the median
If y(x) = 2x-5, then f(4) is A. 17 B.5 C.4 D.3
Answers
Answer:
i think the answer is 3
Step-by-step explanation:
Given m|n, find the value of x.
(8x+6) (9x-30)
Answers
Step-by-step explanation:
(8x+6) (9x-30)
=72x²-240x+54x-180
=72x²-186-180
Answer:
(8x+6) (9x-30)
=72x²-240x+54x-180
=72x²-186-180
Step-by-step explanation:
determine the angle of x :p

Answers
Answer:
x=-10 I think?? because they are congruent
whats 100+100+100+100+100+100+66?
anyways look guys its me!11!! AHhHHhhHHHhhHhHHHhhHHH

Answers
Answer:
666 is the answer now give me my points jk
Step-by-step explanation:
Answer:
Yayyyy that's awesome keep up the good work
Step-by-step explanation:
Thanks for the points:)
2 3 4 5 6 7 8 9 10 TIME REMAINING 54:22 Which is true regarding the system of equations? 6 x + 2 y = 46. 3 x + y = 23. The system results in a false statement. The system results in an intersection at one point. The system results in parallel lines. The system results in a true statement because they are the same line.
Answers
Answer:
system results in a true statement
Step-by-step explanation:
Answer: D is the answer
Step-by-step explanation:
For the following, write out each term of the summation in the boxes provided. Then compute the sum.
a) ∑i=151i = + + + + =
b) ∑i=16(−1)ii = + + + + + =
c) ∑i=14(1i−1i+1) = + + + =
Answers
a) For this summation, we are summing the values of i from 1 to 5. So the terms are 1, 2, 3, 4, 5. Writing them out in the boxes, we get:
1 + 2 + 3 + 4 + 5 =
To compute the sum, we simply add up the terms:
1 + 2 + 3 + 4 + 5 = 15
b) For this summation, we are summing the values of (-1)^i * i from 1 to 6. So the terms are -1, 2, -3, 4, -5, 6. Writing them out in the boxes, we get:
-1 + 2 - 3 + 4 - 5 + 6 =
To compute the sum, we simply add up the terms:
-1 + 2 - 3 + 4 - 5 + 6 = 3
c) For this summation, we are subtracting the value of 1/i+1 from 1/i for i from 1 to 4. So the terms are 1/2 - 1/1, 1/3 - 1/2, 1/4 - 1/3. Writing them out in the boxes, we get:
(1/2 - 1/1) + (1/3 - 1/2) + (1/4 - 1/3) =
To compute the sum, we simply add up the terms:
(1/2 - 1/1) + (1/3 - 1/2) + (1/4 - 1/3) = 5/12
To know more about summation visit:
https://brainly.com/question/29334900
#SPJ11
show work
only do those
32,34,36,38,40

Answers
Answer: see below
Step-by-step explanation:
\(32)\quad \dfrac{3}{5}(x-12)>x-24\)
3(x - 12) > 5(x - 24)
3x - 36 > 5x - 120
-5x -5x
-2x - 36 > -120
+36 +36
-2x > -84
÷ -2 ↓ ÷ -2
x < 42
Graph: ←------------o
42
34) 6[5y - (3y - 1)] ≥ 4(3y - 7)
6[5y - 3y + 1] ≥ 4(3y - 7)
6{2y + 1] ≥ 4(3y - 7)
12y + 6 ≥ 12y - 28
-12y -12y
6 ≥ -28
TRUE so the solution is All Real Numbers
Graph: ←-----------------------→
36) BC + AC > AB
4 + 8 - AB > AB
12 - AB > AB
+AB +AB
12 > 2AB
÷2 ÷2
6 > AB
AB < 6
\(38)\quad \dfrac{1}{2}(y-16)\geq y+2\quad ;\text{claim}\ y\leq 20\)
Check: let y = 16
then \(\frac{1}{2}\)(16 - 16) ≥ 16 + 2
0 ≥ 18
FALSE so the claim is wrong
40) question not provided in the image so I cannot give a solution.
The graph below represents the solution set of which inequality?
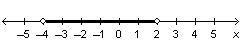
Answers
Answer:
x < 2
Step-by-step explanation:
The indicated part is left from point 2.
You see an open circle at point (2,0) which means you should exclude the point x = 2 in the inequation.
Now you have enough info to get the right inequality:
x < 2
Cronbach's alpha indicates to what extent scale items are correlated to each other?
True
False
Answers
False. Cronbach's alpha is a measure of internal consistency reliability, not a measure of the correlation between scale items.
It assesses the extent to which the items in a scale or questionnaire are measuring the same underlying construct.
Cronbach's alpha is calculated based on the inter-item correlations among the items in a scale. It provides a measure of the average correlation between all possible pairs of items in the scale. The range of Cronbach's alpha is between 0 and 1, with higher values indicating greater internal consistency or reliability.
Essentially, Cronbach's alpha quantifies the extent to which the items in a scale are consistently measuring the same construct or concept. It assesses how well the items "hang together" as a reliable measurement tool.
While correlation between scale items is related to internal consistency, Cronbach's alpha specifically measures the degree to which the items are interrelated and provides a single coefficient that reflects the overall reliability of the scale. It does not directly indicate the extent of item-item correlations or the strength of individual item contributions to the scale.
Learn more about questionnaire at: brainly.com/question/27972710
#SPJ11
a bag of chocolates is labeled to contain 0.384 pounds of chocolate. the actual weight of the chocolates is 0.3798 pounds. how much lighter is the actual weight?
Answers
The actual weight is 0.0042 pounds lighter than the labeled weight.
The actual weight of the chocolates is 0.3798 pounds, while the label on the bag states it should weigh 0.384 pounds. To determine how much lighter the actual weight is, we can calculate the difference between the two weights.
Subtracting the actual weight from the labeled weight, we get:
0.384 pounds - 0.3798 pounds = 0.0042 pounds.
Therefore, the actual weight is 0.0042 pounds lighter than the labeled weight.
It's important to note that this difference may seem small, but it can be significant depending on the context. Accuracy in labeling is crucial for various reasons, such as complying with regulations, providing precise information to consumers, and ensuring fair trade practices. Even minor discrepancies can impact trust and customer satisfaction.
For more information on actual weight visit: brainly.com/question/31170036
#SPJ11
What are the roots of the equation 4x^2 + 16x + 25 = 0 in simplest a + bi form?
Answers
Answer:-2 + 3i/2, and -2-3i/2
Step-by-step explanation:
Apply the quadratic formula.
We have (-16 +-sqrt(16^2-4*4*25))/8.
Simplifying, we have (-16+-12i)/8.
Thus, the roots are -2 + 3i/2, and -2-3i/2
Answer:
The roots are
\(x = - 2 + \frac{3}{2} \: i \: \: \: \: or \: \: \: \: x = - 2 - \frac{3}{2} \: i \\ \)Step-by-step explanation:
4x² + 16x + 25 = 0
Using the quadratic formula
That's
\(x = \frac{ - b\pm \sqrt{ {b}^{2} - 4ac } }{2a} \)From the question
a = 4 , b = 16 , c = 25
Substitute the values into the above formula and solve
We have
\(x = \frac{ - 16\pm \sqrt{ {16}^{2} - 4(4)(25)} }{2(4)} \\ x = \frac{ - 16\pm \sqrt{256 - 400} }{8} \\ x = \frac{ - 16\pm \sqrt{ - 144} }{8} \\ x = \frac{ - 16\pm12 \: i}{8} \\ \)Separate the real and imaginary parts
That's
\(x = \frac{ - 16}{8} \pm \frac{12}{8} \: i \\ x = - 2\pm \frac{3}{2} i\)We have the final answer as
\(x = - 2 + \frac{3}{2} \: i \: \: \: \: or \: \: \: \: x = - 2 - \frac{3}{2} \: i \\ \)Hope this helps you
Can someone help me asap? It’s due today!! I will give brainliest if it’s all correct!!

Answers
Answer:
1) b. 3
2) a. 5
3) c. 4
4) d. 6
Step-by-step explanation:
A coin is tossed and an eight-sided die numbered 1 through 8 is rolled. Find the probability of tossing a tail and then rolling a number greater than 2. The probability of tossing a tail and then rolling a number greater than 2 is ___
Answers
Given that:
- A coin is tossed.
- An eight-sided dice is rolled. This is numbered 1 through 8.
1. By analyzing the information provided in the exercise, you can identify that tossing a coin and getting a tail; and rolling a dice getting a number greater than 2 are Independent Events.
2. Knowing that the probability of occurring two independent events together is equal to the product of their probabilities:
• Let be "A": Tossing a tail.
,• Let be "B": Rolling a number greater than 2.
3. Then, the formula is:
\(P(A\cap B)=P(A)\cdot P(B)\)4. You need to find:
\(\begin{gathered} P(A) \\ P(B) \end{gathered}\)You can determine that:
\(P(A)=\frac{1}{2}\)Because the coin only has two faces.
And:
\(P(B)=\frac{6}{8}=\frac{3}{4}\)Because the dice has 8 sides and you need to find a number greater than 2. This gives you a set of 6 possible values:
\(\lbrace3,4,5,6,7,8\rbrace\)Finally, substituting values into the formula and evaluating, you get:
\(P(A\cap B)=\frac{1}{2}\cdot\frac{3}{4}=\frac{1\cdot3}{2\cdot4}=\frac{3}{8}\)Hence, the answer is:
The probability of tossing a tail and then rolling a number greater than 2 is:
\(P(A\cap B)=\frac{3}{8}\)4.7 squared +7. Three squared -2×4. 7×7. Three times cos 37
Answers
Answer:
135.55
Step-by-step explanation:
PLEASE ANSWER!! WILL GIVE BRAINLIEST

Answers
Answer:
the correct answer is option D

When can parallelism make your algorithms run faster when could it make your algorithms run slower?
Answers
When an algorithm necessitates extensive sharing of instantaneous results, parallelism slows it down. Because there are multiple independent parallel processes and the right number of threads, parallelism will speed up an algorithm.
What algorithm is parallelizable?The ones with data dependencies are the most challenging. It will be exceedingly challenging, for instance, if you are dealing with a vector and the input for the computation at point n depends on the output at position n-1.
When this occurs, you must comprehend what the original algorithm is doing and take an alternative approach. For the aforementioned case, it might be a difficulty with digital signal processing including a feedback-containing digital filter. These are challenging to parallelize, but that is not the sole solution. Instead, you might use the filter and signal's fast Fourier transforms, multiply them, and then perform the inverse transform. All of these operations can be partially parallelized.
To know more about Fourier transforms visit: https://brainly.com/question/1597221
#SPJ4
2. pvalue
3.critical value
4.test value
5.make a desision
Noise Levels in Hospitals In a hospital study, it was found that the standard deviation of the sound levels from 30 areas designated as "casualty doors" was 6.4 dBA and the standard deviation of 28 areas designated as operating theaters was 4.1 dBA. At a 0.10, can you substantiate the claim that there is a difference in the standard deviations? Use a, for the standard deviation of the sound levels from areas designated as "casualty doors." Part 1 of 5 (a) State the hypotheses and identify the claim. H_0: sigma_1^ = sigma_2^ _____
H_1: sigma_1^ ≠ sigma_2^ _____
This hypothesis test is a___test.
Answers
The hypotheses for the test are H₀: σ₁² = σ₂² and H₁: σ₁² ≠ σ₂². This is a two-tailed test to assess if there is a difference in the standard deviations of sound levels between the areas designated as "casualty doors" and operating theaters. The claim being investigated is whether or not there is a difference in the standard deviations.
The hypotheses for the test are:
H₀: σ₁² = σ₂² (There is no difference in the standard deviations of the sound levels between the areas designated as "casualty doors" and operating theaters.)
H₁: σ₁² ≠ σ₂² (There is a difference in the standard deviations of the sound levels between the areas designated as "casualty doors" and operating theaters.)
This hypothesis test is a two-tailed test because the alternative hypothesis is not specifying a direction of difference.
To substantiate the claim that there is a difference in the standard deviations, we will conduct a two-sample F-test at a significance level of 0.10, comparing the variances of the two groups.
To know more about hypothesis test refer here:
https://brainly.com/question/29996729#
#SPJ11
Maria has made $28 selling bracelets at a craft fair. She spends $52 on supplies to make the bracelets. She sells each bracelet for $3. Which inequality can Maria use to find how many more bracelets she needs to sell to make more money than she spent on supplies. A. 3x + 52 < 28 B. 28x +3 >52 C. 3x + 28 < 52 D. 3x +28 > 52
Answers
Answer: D. 3x +28 > 52
Step-by-step explanation:
Based on the information given, the inequality that Maria can use to find how many more bracelets she needs to sell to make more money than she spent on supplies will be calculated thus:
With the question above, the total sales must be greater than the amount spent on supplies. Let the number of bracelets that needs to be sold be represented by x.
Therefore, (3 × x) + 28 > 52
= 3x + 28 > 52.
We can calculate further
3x > 52 - 28
3x > 24
x > 24/3
x > 8
Therefore, 9 or more bracelets needs to be sold since x is greater than 8.
Therefore, the correct option is D 3x +28 > 52
Answer:
D. 3x + 28 > 52
Step-by-step explanation:
(4 x superscript a baseline) superscript b baseline = startfraction 256 over x superscript 8 endfraction?
Answers
The equation (4^a)^b = 256 / x^8 is given. We need to solve for the values of a and b.
To solve the equation (4^a)^b = 256 / x^8, we can simplify the left side of the equation using the exponent rules.
Recall that when we raise an exponent to another exponent, we multiply the exponents. Applying this rule, we have (4^a)^b = 4^(a*b).
Now, the equation becomes 4^(a*b) = 256 / x^8.
To further simplify, we need to express both sides of the equation with the same base. Since 256 is a power of 4 (4^4 = 256), we can rewrite the right side as 4^(4 * (8/2)) = 4^(4 * 4) = 4^16.
Therefore, we have 4^(a*b) = 4^16. In order for the bases to be equal, the exponents must also be equal.
Hence, we have a*b = 16.
To solve for the values of a and b, we need additional information or constraints provided in the problem. Without such information, we cannot determine the specific values of a and b that satisfy the equation.
Learn more about equation: brainly.com/question/29174899
#SPJ11
Complete Question - What are the values of a and b in the equation (4 x Superscript a Baseline) Superscript b Baseline = StartFraction 256 Over x Superscript 8 EndFraction?
Solve by completing the square 5x^2+7k+76=9x+4x^2
Answers
the solution to the equation by completing the square is: x = (9/2) ± √(-7k - 47/4).
To solve the given equation by completing the square, we need to rewrite the equation in the form of \((x + a)^2 = b\) , where a and b are constants. This can be done by following these steps:
1. Move all the terms to one side of the equation:
\(5x^2 + 7k + 76 - 9x - 4x^2 = 0\)
2. Combine like terms:
\(x^2 - 9x + 7k + 76 = 0\)
3. Rewrite the equation by completing the square for the x terms. To do this, take half of the coefficient of x (-9/2), square it, and add it to both sides of the equation:
\(x^2 - 9x + (-(9/2))^2 + 7k + 76 - (-(9/2))^2 = (-(9/2))^2\)
4. Simplify:
\((x - (9/2))^2 + 7k + 76 - (81/4) = 81/4\)
5. Combine constants:
\((x - (9/2))^2 + 7k + 47/4 = 0\)
6. Solve for x by taking the square root of both sides:
x - (9/2) = ±√(-7k - 47/4)
7. Add (9/2) to both sides:
x = (9/2) ± √(-7k - 47/4)
Therefore, the solution to the equation by completing the square is: x = (9/2) ± √(-7k - 47/4).
To know more about completing the square click here:
https://brainly.com/question/8631373
#SPJ4
Assume that y varies inversely with x. if y=4 when x=8, find y when x=2. write and solve an inverse variation equation to find the answer.
Answers
The inverse variation equation is y = k/x where k is the constant of proportionality; when x = 2, y = 16.
What is the inverse variation equation?y = k/x
Where,
k = constant of proportionality
When y = 4; x = 8
y = k/x
4 = k/8
k = 4 × 8
k = 32
When x = 2
y = k/x
y = 32/2
y = 16
Hence, the value of y when x = 2 is 16
Read more on variation:
https://brainly.com/question/13998680
#SPJ1
Determine the value of the variable from the image below.

Answers
Answer:
x=29Step-by-step explanation:
to understand the solving stepsyou need to know about:right angleequationPEMDASto solve:xlet's solve:a right angle contains 90° (always)
according to the question
x+3+x-1+x+1=90
3x3=90
x=87
x=29
solved8.7. let s = {x ∈ z : ∃y ∈ z,x = 24y}, and t = {x ∈ z : ∃y,z ∈ z,x = 4y∧ x = 6z}. prove that s 6= t.
Answers
since we have found an element (48) in S that is not in T, we can conclude that S is not equal to T.
To prove that S is not equal to T, we need to show that there I an element in either S or T that is not in the other set.
Let's first look at the elements in S. We know that S is the set of all integers that can be expressed as 24 times some other integer. So, for example, 24, 48, 72, -24, -48, -72, etc. are all in S.
Now, let's look at the elements in T. We know that T is the set of all integers that can be expressed as 4 times some integer and 6 times some integer. We can find some examples of numbers in T by finding the multiples of the LCM of 4 and 6, which is 12. So, for example, 12, 24, 36, -12, -24, -36, etc. are all in T.
Now, let's consider the number 48. We know that 48 is in S, since it can be expressed as 24 times 2. However, 48 is not in T, since it cannot be expressed as 4 times some integer and 6 times some integer. This is because the only common multiple of 4 and 6 is 12, and 48 is not a multiple of 12.
Learn more about S: https://brainly.com/question/14453211
#SPJ11
find the general solution of the given differential equation. (x + 1) dy dx + (x + 2)y = 2xe−x
Answers
The general solution of the given differential equation (x + 1) dy/dx + (x + 2)y = 2\(xe^{-x}\) is y = \(Cx^{-x}\) + x - 2, where C is a constant.
In order to find the general solution, we can rearrange the equation by dividing both sides by (x + 1):
dy/dx + (x + 2)/(x + 1)y = 2\(xe^{-x}\)/(x + 1).
Next, we notice that the left-hand side can be rewritten as the derivative of y with respect to x times a function of x. This suggests that the equation can be solved using an integrating factor. The integrating factor is given by the exponential of the integral of (x + 2)/(x + 1) with respect to x:
IF = e^{(∫(x + 2)/(x + 1) dx) } = \(e^{x+2}\)ln|x + 1|.
multiplying both sides of the equation by the integrating factor, we obtain:
\(e^{x+2}\)ln|x + 1|dy/dx + (x + 2)\(e^{x+2}\)ln|x + 1|y = 2xe^(-x)\(e^{x+2}\)n|x + 1|.
Simplifying the equation further, we have:
d/dx (\(e^{x+2}\)ln|x + 1|y) = 2xln|x + 1|.
Integrating both sides with respect to x, we get:
\(e^{x+2}\)ln|x + 1|y = x^2ln|x + 1| + C,
where C is the constant of integration. Finally, solving for y, we obtain the general solution:
y = (\(x^{2}\)ln|x + 1| + C)/(\(e^{x+2}\)ln|x + 1|) = Ce^(-x) + x - 2,
learn more about integration here:
https://brainly.com/question/31744185
#SPJ11