An interior designer charges $80 to visit a site, plus $65 to design each room. Identify a function that represents
the total amount he charges for designing a certain number of rooms. What is the value of the function for an
input of 5, and what does it represent?
Answers
The function that represents the total amount he charges is y = 80 + 65x and the total amount he charges for designing 5 rooms is $405
Identify a function that represents the total amount he charges for designing a certain number of roomsThe given parameters are
Charge = $80
Rate = $65 per design
The function is then calculated as
y = Charge + Rate * x
Where
y represents the total amount
x represents the number of rooms
So, we have
y = 80 + 65x
What is the value of the function for an input of 5, and what does it represent?Here, we have
x = 5
So, we have
y = 80 + 65 x 5
Evaluate
y = 405
Hence, the total amount he charges for designing 5 rooms is $405
Read more about linear functions at
https://brainly.com/question/15602982
#SPJ1
Related Questions
Write the second equation in the system of
equations that would produce a graph with
parallel lines.
Answers
If the first equation is in format y=mx+b, (if not convert to it) the second equation would have the same m value, and any b value.
The same value indicates that they have the same slope, therefore parallel.
In what ratio must 40m3 be decreased to become 24m3?
Answers
Answer:
40m3 must be decreased by 40% to become 24m3.
Step-by-step explanation:
To determine in what ratio must 40m3 be decreased to become 24m3, the following calculation must be performed:
40 = 100
24 = X
24 x 100/40 = X
2400/40 = X
60 = X
100 - 60 = 40
Therefore, 40m3 must be decreased by 40% to become 24m3.
Determine whether the given relation is an implicit solution to the given differential equation. Assume that the relationship does define y implicitly as a function of x and use implicit differentiation.
Answers
If it is not true, then the relation is not an implicit solution to the differential equation.
You have not provided the given relation and differential equation, so I will provide general steps to determine whether a given relation is an implicit solution to a differential equation using implicit differentiation and assuming that the relation defines y implicitly as a function of x.
1. Differentiate the relation with respect to x using implicit differentiation.
2. Substitute y' for dy/dx.
3. Simplify the resulting expression by collecting like terms.
4. Substitute the original relation into the simplified expression to obtain a statement that must be true if the relation is an implicit solution to the differential equation.
5. Check whether the resulting statement is true for all values of x and y that satisfy the original relation. If it is true, then the relation is an implicit solution to the differential equation.
To learn more about : equation
https://brainly.com/question/17145398
#SPJ8
Every integer is a rational number.
True or false
Answers
Answer:
Every integer is a rational number. The statement is true. An integer is a number with no decimal or fractional part, from the set of negative and positive numbers, including zero.
For example, lets use the integer, -5.
If it was rational number it would need to be either a decimal or fraction.
So -5 is not a rational number and is an integer.
If the number was 0.5 or 1/5, the number would have been rational.
Inconclusion your statement is true.
The form of malnutrition in which children appear to be of normal weight but are shorter than they should be for their age is termed
Answers
Stunting is the term used to describe a form of malnutrition in which children have a low height-for-age ratio. It is characterized by children appearing to have normal weight but being shorter than they should be for their age.
Stunting is a result of chronic malnutrition, typically experienced during the first 1,000 days of a child's life, from conception to the age of two.
Stunting is a prevalent issue in many developing countries, where access to nutritious food, clean water, and proper healthcare may be limited. It is primarily caused by a lack of adequate nutrition, particularly a deficiency in essential nutrients such as protein, vitamins, and minerals. Additionally, factors like poor sanitation, recurrent infections, and inadequate maternal and child care contribute to stunting.
The consequences of stunting are significant and long-lasting. It affects not only physical growth but also cognitive development, immune function, and overall well-being. Stunted children are at a higher risk of developmental delays, reduced learning capacity, and increased susceptibility to diseases. The impact of stunting can extend into adulthood, leading to reduced productivity and economic potential.
Addressing stunting requires comprehensive interventions that focus on improving maternal and child nutrition, access to clean water and sanitation, and healthcare services. Promoting exclusive breastfeeding, providing nutrient-rich foods, and implementing public health programs are essential in combating stunting and ensuring optimal growth and development for children.
To learn more about ratio, click here: brainly.com/question/24643676
#SPJ11
what is the equation of y=x^3 with the given transformations
Answers
Each transformation affects the shape and position of the graph. It is important to carefully consider the order of the transformations and their impact on the equation.
1. Horizontal Shift (c):
If there is a horizontal shift, the equation becomes y = (x - c)^3.
For example, if there is a shift of 2 units to the right, the equation would be y = (x - 2)^3.
2. Vertical Shift (d):
If there is a vertical shift, the equation becomes y = x^3 + d.
For example, if there is a shift of 3 units upwards, the equation would be y = x^3 + 3.
3. Vertical Stretch (a):
If there is a vertical stretch or compression, the equation becomes y = a * x^3.
For example, if there is a vertical stretch by a factor of 2, the equation would be y = 2 * x^3.
4. Reflection (along the x-axis):
If there is a reflection along the x-axis, the equation becomes y = -x^3.
This flips the graph of the original function upside down.
5. Reflection (along the y-axis):
If there is a reflection along the y-axis, the equation becomes y = (-x)^3.
This mirrors the graph of the original function.
6. Combined Transformations:
If there are multiple transformations, we can apply them in the order they are given. For example, if there is a vertical stretch by a factor of 2 and a horizontal shift of 3 units to the right, the equation would be y = 2 * (x - 3)^3.
Remember, each transformation affects the shape and position of the graph. It is important to carefully consider the order of the transformations and their impact on the equation.
To know more about equation here:
brainly.com/question/29292690
#SPJ11
Which sum or difference is modeled by the algebra tiles?-1OA (x2 - 2x + 3) - (-x2 - 4x - 2) = 2x - 1OB. (x2 - 2x - 3) + (x2 - 4x + 2) = 2x - 1OC. 02 - 2x - 3) - (x2 + 4x + 2) = 2x - 1OD. (x2 - 2x-3) + (-x2 + 4x + 2) = 2x - 1© 2021 Edmentum. All rights reserved.

Answers
Okay, here we have this:
We will take as the first term the upper squares and as the second term the lower ones, and we obtain that:
\(\begin{gathered} (x^2-x-x-1-1-1)+(-x^2+x+x+x+x+1+1) \\ =(x^2-2x-3)+(-x^2+4x+2) \\ =2x-1 \end{gathered}\)Here we obtain that the correct answer is the option D.
I need help ASAP !!
Find the length of a
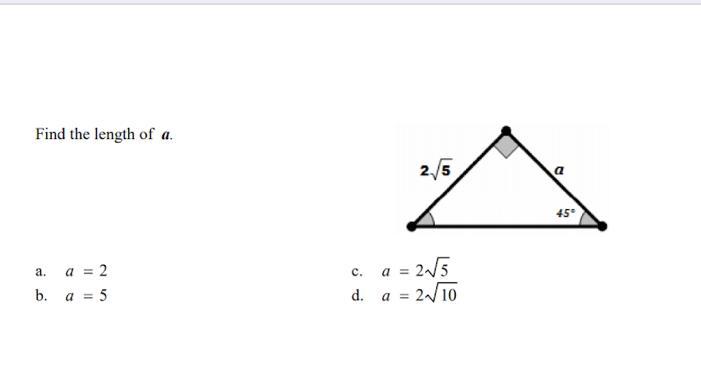
Answers
Step-by-step explanation:
Please refer to the attachment
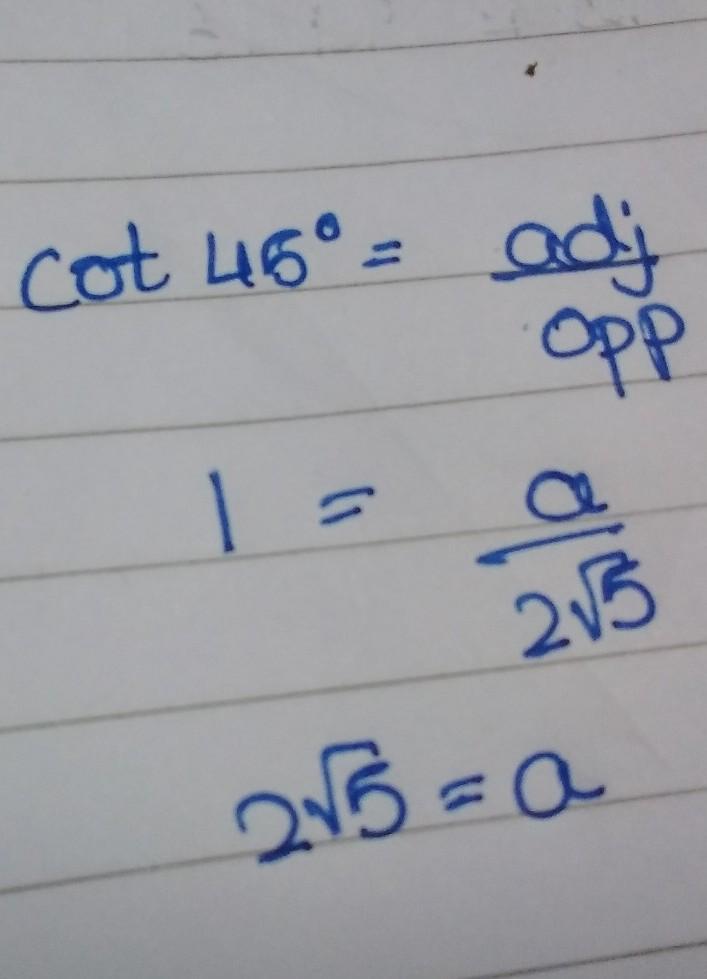
which is bigger -24/5 or -11/2
Answers
Answer:
-24/5
Step-by-step explanation:
which is bigger -24/5 or -11/2?
-24/5 = -4.8
-11/2 = -5.5
-5.5 < -4.8
So, -24/5 is bigger.
a student takes a true-false test that has 14 questions and guesses randomly at each answer. let x be the number of questions answered correctly. find p(5) group of answer choices 0.0001 0.0611 0.1833 0.1222
Answers
The probability to answer 5 questions correctly from 14 true or false questions is 0.1222
The given situation represents a binomial experiment, where there are only two possible outcomes for each trial: success (answering correctly) and failure (answering incorrectly). To find the probability of a particular number of successes, we use the binomial probability formula:
P(x)= nCx × p^x × q^(n-x)
Where, n is the total number of trials, p is the probability of success on each trial, q is the probability of failure on each trial (1-p), and x is the number of successes desired.
n = 14 (total number of questions)
p = 1/2 (probability of answering correctly when guessing randomly), and q = 1/2 (probability of answering incorrectly when guessing randomly).
To find P(5), we substitute these values in the formula
P(5) = 14C5 * (1/2)^5 * (1/2)^9= 2002 * (1/32) * (1/512)= 2002 / 16384≈ 0.1222
Therefore, the answer is option D, 0.1222.
To learn more about Binomial experiment:https://brainly.com/question/9325204
#SPJ11
Read the following statements I through V: 1. Zero (0) II. One (1) III. Two (2) IV. Either Zero (0) or One (1) V. Neither Zero (0) nor One (1) What is the skewness of the normal distribution? 1 II III IV V II or III None of the above
Answers
Skewness of the normal distribution. When it comes to normal distribution, the skewness is equal to zero.
Skewness is a measure of the distribution's symmetry. When a distribution is symmetric, the mean, median, and mode will all be the same. When a distribution is skewed, the mean will typically be larger or lesser than the median depending on whether the distribution is right-skewed or left-skewed. It is not appropriate to discuss mean or median in the case of normal distribution since it is a symmetric distribution.
Therefore, the answer is None of the above.
In normal distribution, the skewness is equal to zero, and it is not appropriate to discuss mean or median in the case of normal distribution since it is a symmetric distribution.
To know more about Skewness visit:
brainly.com/question/15422644
#SPJ11
Which proportion can you use to find the value of a?

Answers
The proportion used to find the value of a is a/18 = 16/a
What is proportion?Proportion is a mathematical comparison between two numbers. According to proportion, if two sets of given numbers are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other.
Given are three similar triangles, (refer to attached figure to separately see the similar triangles)
We know that, similar triangle have corresponding sides in equal ratio,
Therefore,
a/18 = 16/a
Hence, the proportion used to find the value of a is a/18 = 16/a
Learn more about proportion, click;
https://brainly.com/question/7096655
#SPJ1

calculate vred, the speed of red light in the diamond. to four significant figures, c=2.998×108m/s.
Answers
The speed of red light in a diamond, denoted as vred, is approximately equal to the speed of light in a vacuum, c, which is 2.998 × 10^8 m/s, rounded to four significant figures.
According to the principles of optics and the refractive index of a material, the speed of light in a medium is generally lower than its speed in a vacuum. The refractive index of a diamond is approximately 2.42.
To calculate the speed of red light in a diamond, we can use the formula vred = c / n, where c represents the speed of light in a vacuum and n represents the refractive index of the diamond.
Substituting the given values, we have vred = (2.998 × 10^8 m/s) / 2.42. Evaluating this expression yields a result of approximately 1.239 × 10^8 m/s.
Rounding this value to four significant figures, we obtain the speed of red light in a diamond, vred, as approximately 1.239 × 10^8 m/s.
Therefore, the speed of red light in a diamond, rounded to four significant figures, is approximately 1.239 × 10^8 m/s, which is slightly lower than the speed of light in a vacuum, c.
Learn more about principle of optics here:
https://brainly.com/question/28174932
#SPJ11
a) x^2-2x+1=0
b) x^3-3x^2x+3x-1=0
Find x.
Answers
Part (a)
\((x-1)^2=0 \implies x=\boxed{1}\)
Part (b)
\(x^3-3x^2 x+3x-1=0 \\ \\ -2x^3+3x-1=0\)
By inspection, x=1 is a root, so we can consider dividing by x-1.
\(\frac{-2x^3+3x-1}{x-1}=-2x^2-2x+1 \\ \\ \implies (x-1)(-2x^2-2x+1)=0 \\ \\ x-1=0 \implies x=\boxed{1} \\ \\ -2x^2-2x+1=0 \implies x=\frac{2 \pm \sqrt{4+8}}{-4} \\ \\ =\boxed{\frac{-1 \pm \sqrt{3}}{2}}\)
Write an ordered pair that is a solution of each system of inequalities.
x + y > 2 , 3x + 2y ≤ 6
Answers
The ordered pair (1, 2) is a solution to the system of inequalities
x + y > 2 and
3x + 2y ≤ 6.
To find an ordered pair that is a solution to the system of inequalities:
Start with the first inequality:
x + y > 2.
Choose a value for x and y that satisfies this inequality. For example, let's choose
x = 1 and
y = 2.
Substituting these values into the inequality:
1 + 2 > 2, which is true.
Now, let's move to the second inequality:
3x + 2y ≤ 6.
Substitute the same values, x = 1 and
y = 2, into this inequality:
3(1) + 2(2) ≤ 6.
Simplifying, we have:
3 + 4 ≤ 6, which is true.
Therefore, the ordered pair (1, 2) is a solution to the given system of inequalities.
Hence the ordered pair (1, 2) is a solution to the system of inequalities
x + y > 2 and 3x + 2y ≤ 6.
To know more about inequalities, visit:
https://brainly.com/question/28053239
#SPJ11
3 3 Luke started a weight-loss program. The first week, he lost x pounds. The second week, he lost 2 pounds less than 2 times the pounds 3 he lost the first week. The third week, he lost 1 pound more than ã of the pounds he lost the first week. 3 Liam started a weight-loss program when Luke did. The first week, he lost 1 pound less than 2 times the pounds Luke lost the first 5 week. The second week, he lost 4 pounds less than 2 times the pounds Luke lost the first week. The third week, he lost 2 pound more 5 than 3 times the pounds Luke lost the first week. Assuming they both lost the same number of pounds over the three weeks, complete the following sentences. 4 pounds 6 pounds 21 4 2 pounds 13 - 40Luke started a weight loss program the first week he lost X pounds the second week he lost 3/2 pounds less than 3/2 times the pounds he lost the first week the third week he lost 1 pound more than three-fourths of the Pouncey lost the first week
Answers
We know that Luke lost x pounds the first week.
We also know that the second week 3/2 less than 3/2 times the pounds he lost the first week, this means that the secons week he lost:
\(\frac{3}{2}x-\frac{3}{2}\)Finally the third week he lost 1 pound more than 3/4 of the pounds he lost the first week. This can be written as:
\(\frac{3}{4}x+1\)Hence luke lost a total of:
\(x+\frac{3}{2}x-\frac{3}{2}+\frac{3}{4}x+1=\frac{13}{4}x-\frac{1}{2}\)Therefore the expression for Luke's weight loss is:
\(\frac{13}{4}x-\frac{1}{2}\)Liam lost the first week 1 pound less than 3/2 times the loss Luke had the first week this can be express as:
\(\frac{3}{2}x-1\)The second week he lost 4 pounds less than 5/2 times the loss of Luke the firs week then we have:
\(\frac{5}{2}x-4\)Finally Liam lost 1/2 pound more than 5/4 times the loss of Luke the first week, then:
\(\frac{5}{4}x+\frac{1}{2}\)Adding this we have:
\(\frac{3}{2}x-1+\frac{5}{2}x-4+\frac{5}{4}x+\frac{1}{2}=\frac{21}{4}x-\frac{9}{2}\)Therefore Liam's expression is:
\(\frac{21}{4}x-\frac{9}{2}\)Now, we know that both of them lost the same weight, then we have the equation:
\(\frac{13}{4}x-\frac{1}{2}=\frac{21}{4}x-\frac{9}{2}\)Solving for x we have:
\(\begin{gathered} \frac{13}{4}x-\frac{1}{2}=\frac{21}{4}x-\frac{9}{2} \\ \frac{21}{4}x-\frac{13}{4}x=\frac{9}{2}-\frac{1}{2} \\ \frac{8}{4}x=4 \\ x=\frac{4}{\frac{8}{4}} \\ x=2 \end{gathered}\)Therefore Luke lost 2 pound the first week.
Finally we plug the value of x in the expression for Luke's weight loss to get the total amount over the three weeks:
\(\begin{gathered} \frac{13}{4}(2)-\frac{1}{2}=\frac{13}{2}-\frac{1}{2} \\ =\frac{12}{2} \\ =6 \end{gathered}\)Therefore they lost 6 pounds in three weeks.
Please help!!! What are the domain and range of the function?

Answers
Answer: Option D
Step-by-step explanation:
Step-by-step explanation:
As we know domain of a function is represented by x values on the graph and y values represents the range of the function.
From the given table domain will be the set of all real numbers.
Range of the same function will be y > 4
Option D is the answer. there you go o(* ̄︶ ̄*)o it was hard to but now its easy
someone help
thank you

Answers
Answer:
30000+200000
Step-by-step explanation:15% bc its 3 years, 15% of 200000 is 30000
Answer: 230 000
Step-by-step explanation:
2017 - 2014 = 3
if each year it goes up by 5% and it's already been 3 yrs.
then 3 x 5 = 15%
now it's at 15 %
Value :
200 000(0.15)
= 30 000
Cost of house after 3 yrs :
200 000 + 30 000
= 230 000
10 points if somone gets it right
Tran oversees filling the popcorn machine at the local movie theater. The dimensions of the popcorn machine are shown below. The machine currently has 1,425 cubic inches of popcorn inside.
20 in 25 in 15 in
What is the volume of the popcorn that must be added to the machine? Your answer must be exact or accurate to the nearest hundredth
Answers
Answer:
6,075
Step-by-step explanation:
To find the volume of popcorn that must be added to the machine, we need to calculate the difference between the current volume and the maximum volume of the machine.
The volume of the popcorn machine can be calculated by multiplying its dimensions:
Volume = Length × Width × Height
Given dimensions:
Length = 20 inches
Width = 25 inches
Height = 15 inches
Volume of the machine = 20 in × 25 in × 15 in = 7,500 cubic inches
To find the volume of popcorn that must be added, we subtract the current volume (1,425 cubic inches) from the maximum volume (7,500 cubic inches):
Volume of popcorn to be added = Maximum volume - Current volume
= 7,500 cubic inches - 1,425 cubic inches
= 6,075 cubic inches
Therefore, the volume of popcorn that must be added to the machine is 6,075 cubic inches.
Which best describes the constant difference for the function? a constant second difference of –6 a constant second difference of 8 a constant third difference of –6 a constant third difference of 8
its not a or b
Answers
Answer:
D
Step-by-step explanation:
Evaluate the expression for the given value of x.
4x + 6 for x = 7
The solution is
Answers
28 + 6 = 34
the answer to this equation is 34
Question 1 of 10
What is the equation of the parabola in vertex form?
0=y²-x-4y+3
O A. (x-3)=(y-2)²
O B. (x+12)2 = (y-4)
O c. (x+1)=(y-2)²
O D. (x-1)= (y + 2)²
Answers
3(r+2s)=2t−4
Use the distributive property to multiply 3 by r+2s.
3r+6s=2t−4
Subtract 6s from both sides.
3r=2t−4−6s
The equation is in standard form.
3r=−6s+2t−4
Divide both sides by 3.
3
3r
=
3
−6s+2t−4
Dividing by 3 undoes the multiplication by 3.
r=
3
−6s+2t−4
Divide −4+2t−6s by 3.
r=
3
2t
−2s−
3
4
SOLVE FOR S
Consider the following hypotheses: H0: μ = 120 HA: μ ≠ 120 The population is normally distributed with a population standard deviation of 46. (You may find it useful to reference the appropriate table: z table or t table) a-1. Calculate the value of the test statistic with x−x− = 132 and n = 50. (Round intermediate calculations to at least 4 decimal places and final answer to 2 decimal places.)
Answers
The value of the test statistic for the given hypotheses is -2.6087. To calculate the test statistic, we can use the formula for a one-sample z-test:
z = (x - μ) / (σ / \(\sqrt{(n)}\))
where x is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size.
In this case, the sample mean (x) is 132, the population mean (μ) is 120, the population standard deviation (σ) is 46, and the sample size (n) is 50.
Plugging these values into the formula, we have:
z = (132 - 120) / (46 / sqrt(50))
= 12 / (46 / 7.0711)
= 12 / 6.5203
= 1.8387
Since the alternative hypothesis is μ ≠ 120, we are conducting a two-tailed test. The critical value for a two-tailed test with a significance level of 0.05 is ±1.96.
Comparing the test statistic (1.8387) with the critical value, we find that the test statistic does not fall outside the critical region. Therefore, we do not reject the null hypothesis. This means there is not enough evidence to conclude that the population mean is significantly different from 120 based on the given sample.
To leran more about test statistic, refer:-
https://brainly.com/question/31746962
#SPJ11
To be a member of the choir, you must go to an audition. Henry's cousin is a member of the choir. What conjecture can you make about Henry's cousin?
A.) Henry’s cousin practices with the choir
B.) Henry is in the choir
C.) Henry’s cousin went to an audition
Answers
Answer:
A) Henry’s cousin practices with the choir
Step-by-step explanation:
becuase it says "Henry's cousin is a member of the choir."
Answer:
Henry’s cousin went to an audition.
Step-by-step explanation:
To solve, Use the law of detachment. In geometry, the law of detachment states that if P leads to Q and P is true, then Q must be true. This is written in a different format, but it is once again a conditional statement.
Geometry question help!!

Answers
Answer:
3
Step-by-step explanation:
triangles are congruent too
qr/rx = pr/ry
rx = (6*4)/8 = 3
is (fifteen more than a number) an expression?
Answers
Answer:
yes
Step-by-step explanation:
it is a way of saying x number
example, I have more than one apple. I am expressing that I do not have one apple or no apples.
Scores on the Wechsler Intelligence Scale for Children (WISC) in neurotypical children have a population mean of 100 and a population standard deviation of 15. Assume the population standard deviation is the same in neurotypical and autistic children, but the population mean in autistic children is unknown.
a) Suppose we take a sample of 49 autistic children. What is the critical value (on the x^bar scale) for a one-sided Neyman-Pearson hypothesis test of H0 : μ = 100 vs. H 1 : μ = 95 using alpha = 0.05? Round your answer to 3 decimal places.
b)Using your critical value, what is the power of our test? Express your answer as a decimal rounded to the nearest thousandth (3 decimal places).
c)The probability of committing a Type II Error on this test is:
Answers
a. The critical value for this test is 103.525
b. The power of this test is 0.0001
c. The probability of committing a Type II Error on this test is 0.9999.
How to calculate the valuea) Using a standard normal distribution table or calculator, we can find the Zα value for α = 0.05. The Zα value for α = 0.05 is approximately 1.645.
Plugging in the values into the formula, we get:
Critical value = 100 + 1.645 * (15 / √49)
Critical value = 100 + 1.645 * (15 / 7)
Critical value ≈ 100 + 1.645 * 2.143
Critical value ≈ 100 + 3.525
Critical value ≈ 103.525
b) Using the Z-score formula:
Z = (x - μ) / (σ / √n)
Z = (103.525 - 95) / (15 / √49)
Z = 8.525 / (15 / 7)
Z ≈ 8.525 / 2.143
Z ≈ 3.969
Using a standard normal distribution table or calculator, we can find the probability to the right of Z = 3.969. The power is equal to that probability.
The power ≈ 1 - 0.9999
The power ≈ 0.0001
c) The probability of committing a Type II Error is equal to 1 - power. In this case, the probability of committing a Type II Error is approximately:
= 1 - 0.0001
= 0.9999.
Learn more about probability
https://brainly.com/question/24756209
#SPJ1
Find the volume of a right circular cone that has a height of 12.7 m and a base with a circumference of 18.9 m. Round your answer to the nearest tenth of a cubic meter.
Answers
Answer:
119.64m^3
Step-by-step explanation:
Given that
The height is 12.7 m
And the base with the circumference is 18.9 m
We need to find out the volume of the right circular cone
As for determining it first compute the radius
As we know that
Circumference = 2πr
18.9 = 2 × 3.14 × r
r = 3m
Now the volume is
= 1 ÷ 3πr^2h
= 1 ÷ 3 × 3.14 × 3^2 × 12.7
= 119.64m^3
Find the x-intercept and y-intercept of the line.7x+4y=-28* -intercept: 08coХ5?y -intercept:

Answers
The given equation of the line is:
\(7x+4y=-28\)It is required to find the x-intercept and the y-intercept.
To find the x-intercept, substitute y=0 into the equation and find x:
\(\begin{gathered} 7x+4(0)=-28 \\ \Rightarrow7x=-28 \\ \text{ Divide both sides by }7: \\ \Rightarrow\frac{7x}{7}=\frac{-28}{7} \\ \Rightarrow x=-4 \end{gathered}\)Hence, the x-intercept is -4.
To find the y-intercept, substitute x=0 into the equation and find y:
\(\begin{gathered} 7(0)+4y=-28 \\ \Rightarrow4y=-28 \\ \text{ Divide both sides by }4: \\ \Rightarrow\frac{4y}{4}=\frac{-28}{4} \\ \Rightarrow y=-7 \end{gathered}\)The y-intercept is -7.
Answers:
x-intercept: -4
y-intercepe: -7
x – 11 = 9 i need help
Answers
Answer:
20=x
Step-by-step explanation:
x-11=9
if you switch the equation its 11+9=x
11+9= 20
20-11=9
Answer:
x - 11 = 9
+11 +11
x = 20
Step-by-step explanation: