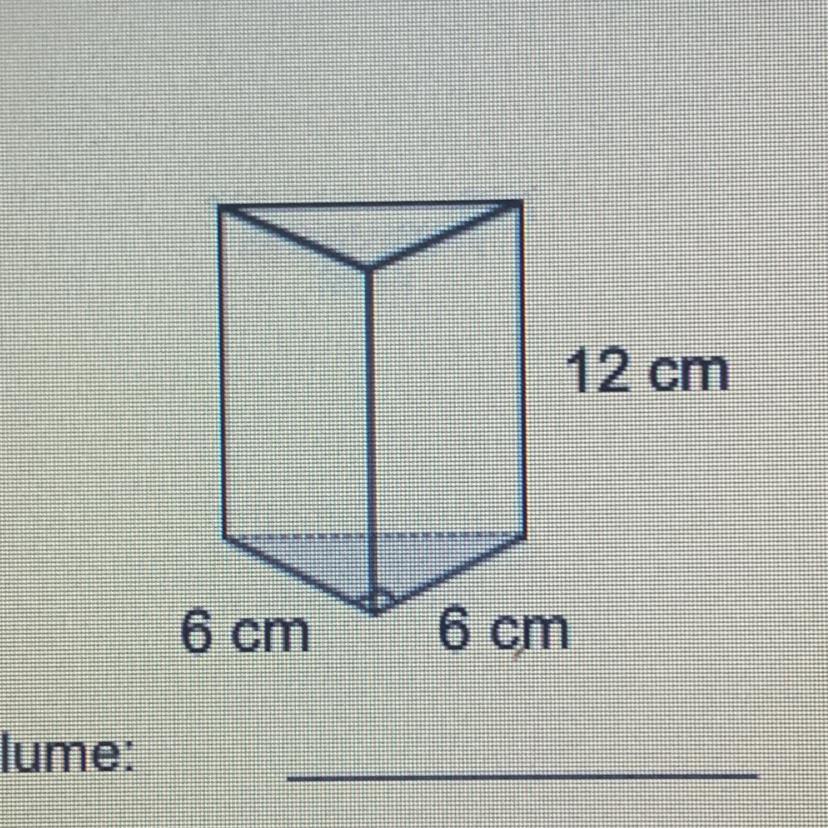
Answers
Answer:
volume=lxbxh
=6*6*12
=432cm^2
Related Questions
please help!
options
A) integer
B) Real
C) Whole
D) irrational

Answers
C. Whole
#CarryOnLearningAnswer:
m
Step-by-step explanation:
Need Help!
A line has a slope of 4 and goes through the point (5,−2). What is the equation of this line in Standard Form?
−4x+y=18
4x+y=−18
−4x+y=−18
−4x+y=−22
Answers
Answer:
-4x+y=-22
Step-by-step explanation:
-4x +y= -22 is the equation of this line in Standard Form .
What is in slope-intercept form?
Y = mx + b, which defines a line, is an equation's slope-intercept form.When a line is graphed, its slope, m, and its point of intersection with the y-axis, b, also known as the y-intercept, are shown.To find answers for x, y, m, and b, utilize slope intercept form.m = 4
the point = (5, -2)
the equation of this line
y - y₁ = m ( x - x₁)
y - ( -2 ) = 4 ( x - 5 )
y + 2 = 4( x - 5 )
y + 2 = 4x - 20
y = 4x - 20 - 2
y = 4x - 22
-4x +y= -22
Learn more about slope-intercept form
brainly.com/question/9682526
#SPJ2
The graph shows the height of a scratch on the edge of a circular gear.
Which function is the best model for the height of the scratch?
a. h(t) = 3.5 sin (π t) + 1.5
b. g(t) = 1.5 sin (π t) +3.5
c. h(t) = 1.5 sin (2 π t) + 3.5
d. h(t) = 1.5 sin (π/2 t) + 3.5
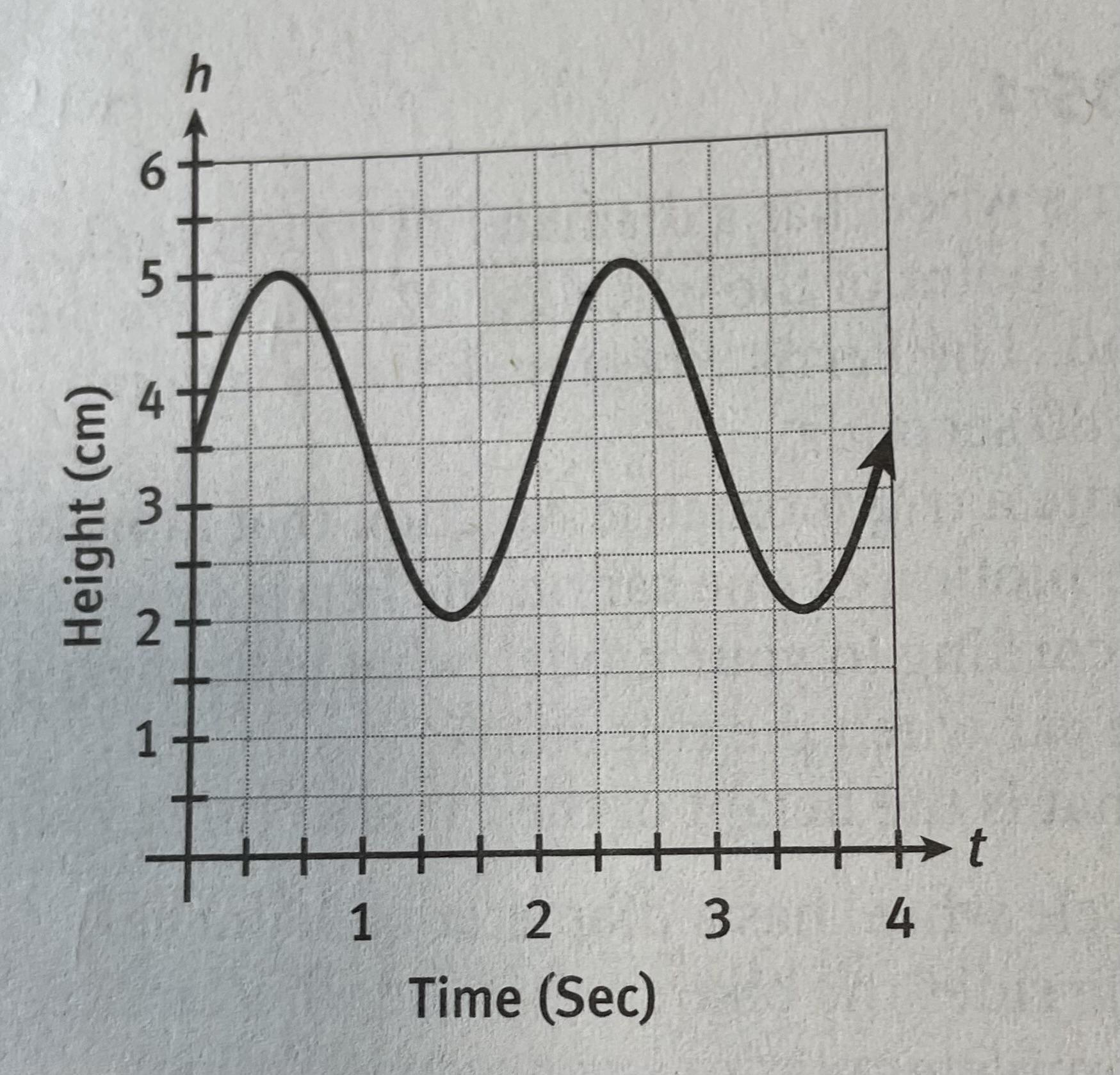
Answers
Answer:
b. g(t) = 1.5 sin (π t) +3.5
Step-by-step explanation:
You want to choose the function that has the given graph.
Test pointsAt t = 0, the graph shows a value of 3.5. The sine of 0 is 0, so this eliminates choice A.
At t = 1/2, the graph shows a value of 5. The values given by the different formulas are ...
b. g(1/2) = 1.5·sin(π/2) +3.5 = 5 . . . . . matches the graph
c. h(1/2) = 1.5·sin(π) + 3.5 = 3.5 . . . . no match
d. h(1/2) = 1.5·sin(π/4) +3.5 = 0.75√2 +3.5 . . . . no match
__
Additional comment
The horizontal distance for one period of the graph (from peak to peak, for example) is T = 2 seconds. If the sine function is sin(ωt), then the value of ω is ...
ω = 2π/T = 2π/2 = π
This tells you the function g(t) = 1.5·sin(πt)+3.5 is the correct choice.
most people complain that they gain weight during the december holidays. to find out how much, we sample the weights of 23 adults in mid-november and again in early to mid-january. the mean weight change for the sample was a gain of 0.11 lbs., with a standard deviation of the differences of 5.25 lbs. find a 82% confidence level for the average weight gain.
Answers
With 82% confidence that the true average weight gain during the December holidays for the sampled adult population is between -1.25 pounds. and 1.47 pounds.
To find the 82% confidence interval for the mean weight gain over the holidays in December, you can use the following formula:
\(CI = xd ± t*(SDd/sqrt(n))\)
where:
xd = average weight change of sample (0.11 lb increase)
SDd = standard deviation of weight difference (5.25 lbs)
n = sample size (23)
t = the critical value of the t distribution with n-1 degrees of freedom and the desired confidence level (82% in this case)
You can use a t-table or a calculator to find the critical value of the t-distribution. With 22 degrees of freedom (n-1) and an 82% confidence level, the critical value is approximately 1.319.
Plugging in the given values gives:
\(CI = 0.11 ± (1.319*(5.25/sqrt(23))) = (-1.25, 1.47)\)
Therefore, we can say with 82% confidence that the true average weight gain during the December holidays for the sampled adult population is between -1.25 pounds. and 1.47 pounds.
Note that the confidence intervals include zero. This means that we cannot reject the null hypothesis that there is no significant difference in weight between mid-November and he early-to-mid-January.
However, this does not necessarily mean no weight gain during his December vacation, as there is individual variation in weight change within the sample.
learn more about standard deviation
brainly.com/question/23907081
#SPJ4
true or false: the graphical method can be used to solve linear programming problems with four decision variables.
Answers
False. The graphical method is only suitable for linear programming problems with two decision variables. For problems with more than two variables, programming techniques such as the simplex method are used.
Variables play a crucial role in both graphical and programming methods as they represent the unknown quantities in the problem.
True, the graphical method can be used to solve linear programming problems with four decision variables. However, it may be more challenging and less efficient compared to other methods, such as the simplex method, when dealing with a higher number of variables.
To know more about Variables click here.
brainly.com/question/17344045
#SPJ11
resolve in factor x³-16x
Answers
Answer:
x (x + 4) (x - 4)
Elena has a shop on Etsy where she makes and sells belts and headbands for girls out of fancy ribbons. Each set uses a total of 1 yard (36 inches) of ribbon. She cuts this into two pieces so that the length of the first piece divided by the length of the second piece has a ratio of 2 to 3.
Answers
Missing part of the question:
Let x represent the length of the first piece. Write an equation that represents the ratio of the first piece of ribbon to the second piece. Be sure to define your variable or variable expressions.
Answer:
\(3x = 2y\)
Step-by-step explanation:
Given
x = first
y = second
Required
Represent as an equation
From the question, when x is divided by y, it gives ratio of 2 to 3.
This implies that:
\(\frac{x}{y} = \frac{2}{3}\)
Cross Multiply
\(3x = 2y\)
What is the absolute value of the number indicated on the number line below?A. -2 2/3B. 2 2/3C. -2 1/2D. 2 1/2

Answers
hello
from the point on the graph, we can notice that it is in between (-3) and (-2) value. this corresponds to -(2 1/2).
But then the absolute value of this number would be
\(\lbrack-2\frac{1}{2}\rbrack=2\frac{1}{2}\)the value of the answer corresponds to option D
Suppose a random sample of 44 OSU students’ IQ exam scores had a sample average
of 105 points. It is known that the population standard deviation of IQ exam scores
is σ = 15 points. Find a 90% confidence interval for the mean OSU students’ IQ exam
score. Justify the relevant confidence interval conditions are met.
Answers
The 90% confidence interval for the mean OSU students’ IQ exam scores is:
105 ± 4.42 or (100.58, 109.42) and we have given the justified relevant confidence interval.
What is the confidence interval?
The confidence interval is a statistical range that estimates the unknown true value of a population parameter, such as the mean or the proportion, based on a sample of data. It gives us a range of values in which we are confident that the true population parameter lies with a certain level of certainty or confidence.
In the given example, we want to estimate the mean IQ exam score for all OSU students based on a random sample of 44 students. We know the population standard deviation, which is σ = 15 points. To find a 90% confidence interval for the mean OSU students’ IQ exam score, we can use the following formula:
Confidence interval = sample mean ± margin of error
The margin of error is calculated as follows:
Margin of error = z* (σ/√n)
where z* is the critical value of the standard normal distribution for a 90% confidence level, which can be found using a table or calculator. For a two-tailed test, the critical value is ±1.645.
n is the sample size, which is 44 in this case.
Plugging in the values, we get:
Margin of error = 1.645 * (15/√44) ≈ 4.42
The sample mean is 105 points.
Therefore, the 90% confidence interval for the mean OSU students’ IQ exam score is:
105 ± 4.42 or (100.58, 109.42)
We can justify the relevant confidence interval conditions as follows:
Random sampling: The sample is chosen randomly, which ensures that it is representative of the population.
Independence: The sample observations are independent of each other, which means that the results are not influenced by any external factors.
Normality: The sample size is sufficiently large (n > 30), so we can assume that the sampling distribution of the sample mean is approximately normal.
Population standard deviation is known: We are given that the population standard deviation is σ = 15 points, which allows us to use the normal distribution to find the confidence interval.
Hence, The 90% confidence interval for the mean OSU students’ IQ exam scores is:
105 ± 4.42 or (100.58, 109.42) and we have given the justified relevant confidence interval.
To learn more about the confidence interval, visit:
https://brainly.com/question/17097944
#SPJ1
in three flips of an unfair coin the probability of getting three heads is the same as the probability of getting exactly two tails. what is the ratio of the probability of flipping a tail to the probability of flipping a head?
Answers
The ratio of the probability of flipping a tail to the probability of flipping a head when the probability of getting three heads is the same as the probability of getting exactly two tails in three flips is 1/3.
How to find the ratio of probability of flipping a tail to probability of flipping a head?Let p be the probability of flipping a head and q be the probability of flipping a tail.
The probability of getting three heads in three flips is \((p)^3.\)
The probability of getting exactly two tails in three flips is 3pq².
Given that these probabilities are equal, we have:
\((p)^3\)= 3pq²
Simplifying this equation gives:
p = 3q
Dividing both sides by q gives:
p/q = 3
Therefore, the ratio of the probability of flipping a tail to the probability of flipping a head is 1/3.
Learn more about Probability
brainly.com/question/30034780
#SPJ11
3 - (2x - 5) < -4 (x+2) can someone please help me get the answer i dont know how to get it
Answers
Answer:
x < -8
Step-by-step explanation:
3 - (2x - 5) < -4 (x+2)
distribute
3 - 2x + 5 < -4x - 8
add the numbers
8 - 2x < -4x - 8
move the x
2x < -16
divide
x < -8
Catherine rolls a 6-sided die five times, and the product of her rolls is 300. How many different sequences of rolls could there have been? (The order of the rolls matters.)
Answers
Answer:
There are 15 different sequences of rolls that could have resulted in a product of 300 when rolling a 6-sided die five times.
Step-by-step explanation:
To determine the number of different sequences of rolls Catherine could have had, we need to find the number of ways to express 300 as the product of five factors.
Let's factorize 300:
300 = 2 * 2 * 3 * 5 * 5
Now, we can assign these factors to the five rolls. Since the order of the rolls matters, we can use the concept of permutations.
We have two 2s, one 3, and two 5s. To find the number of different sequences, we need to calculate the permutations of these factors.
The number of permutations of five items taken from a set of two identical items, one identical item, and two identical items can be calculated using the formula:
P(n; n1, n2, ..., nk) = n! / (n1! * n2! * ... * nk!)
Where:
n is the total number of items (5 rolls)
n1, n2, ..., nk are the number of identical items (2, 1, 2)
Using this formula, we can calculate the number of different sequences of rolls:
P(5; 2, 1, 2) = 5! / (2! * 1! * 2!) = (5 * 4 * 3 * 2 * 1) / (2 * 1 * 1 * 2) = 60 / 4 = 15
know more about permutations: brainly.com/question/32683496
#SPJ11
A line is perpendicular to y = -1/5x + 1 and intersects the point negative (-5,1) what is the equation of this perpendicular line?
Answers
Answer: y = 5x + 26
Step-by-step explanation:
To find the equation of a line that is perpendicular to the given line y = -1/5x + 1 and passes through the point (-5, 1), we need to determine the slope of the perpendicular line. The given line has a slope of -1/5. Perpendicular lines have slopes that are negative reciprocals of each other. So, the slope of the perpendicular line will be the negative reciprocal of -1/5, which is 5/1 or simply 5. Now, we have the slope (m = 5) and a point (-5, 1) that the perpendicular line passes through.
We can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Substituting the values, we get:
y - 1 = 5(x - (-5))
Simplifying further:
y - 1 = 5(x + 5)
Expanding the brackets:
y - 1 = 5x + 25
Rearranging the equation to the slope-intercept form (y = mx + b):
y = 5x + 26
Therefore, the equation of the perpendicular line that passes through the point (-5, 1) is y = 5x + 26.
The real solutions to the equation 3x5 + 25x4 + 26x3 – 82x2 + 76x = 48 are shown on the graph. What are the nonreal solutions?
StartFraction 1 + i StartRoot 5 EndRoot Over 3 EndFraction, StartFraction 1 minus i StartRoot 5 EndRoot Over 3 EndFraction.
StartFraction negative 1 + i StartRoot 5 EndRoot Over 3 EndFraction, StartFraction negative 1 minus i StartRoot 5 EndRoot Over 3 EndFraction.
StartFraction negative 1 + StartRoot 5 EndRoot Over 3 EndFraction, StartFraction negative 1 minus StartRoot 5 EndRoot Over 3 EndFraction.
StartFraction 1 + StartRoot 5 EndRoot Over 3 EndFraction, StartFraction 1 minus StartRoot 5 EndRoot Over 3 EndFraction.

Answers
The non-real solutions according to the equation is (1 + √5 i)/3 and (1 - √5 i)/3.
What is Factor theorem?A polynomial can be factored, and its roots can be discovered using the factor theorem. The polynomial residual theorem is indeed a special instance of this one.
A polynomial f(x) has a factor (x-a), as was noted in the beginning, if and only if f(a) = 0.
As per the given equation in the question,
3x⁵ + 25x⁴ + 26x³ - 86x² + 76x - 48
The function can be written as:
f(x) = g(x).h(x) (i)
The real solutions from the graph is,
x₁ = -6, x₂ = -4 and x₃ = 1.
So,
g(x) = (x + 6) × (x + 4) × (x - 1)
g(x) = (x² + 10x + 24) × (x - 1)
g(x) = x³ + 9x² + 14x - 24.
Now, substitute the values in (i)
3x⁵ + 25x⁴ + 26x³ - 86x² + 76x - 48 = (x³ + 9x² + 14x - 24) × (ax² + bx + c)
Therefore,
ax⁵ = 3⁵
a = 3.
-24c = -48
c = 2.
-24(bx) + 14(cx) = 76x
-24b + 28 = 76
b = -2.
The equation for non-real solution:
h(x) = 3x² - 2x + 2.
Δ = b² - 4ac = (-2)² - 4(3)(2) = -20
x₁ = (2 + √20)/6 = (1 + √5 i)/3
x₂ = (2 - √20)/6 = (1 - √5 i)/3
To know more about Factor theorem:
https://brainly.com/question/24545336
#SPJ1
1) Simplify the expression. Show your work.
\(\sqrt\frac{9x^{3} }{4y^2}\)
2) Simplify the expression (2-5i)(3+7i)-(4+3i). Show your work.
3) Simplify the expression \(\sqrt[3]{81}x^{7}y^{9}z^{5}\) . Show your work.
Answers
The expressions are simplified to 3x^3/2/ y , 2 - 4i - 35i² and 4x^7y^9z^5
How to simply the expressions1.
Given the expression;
\(\sqrt{\frac{9x^3}{4y^2} }\)
Take the square root of the variables;
= \(\frac{3x^3^/^2}{y}\)
2. (2-5i)(3+7i)-(4+3i)
expand the bracket
6 + 14i - 15i - 35i² - 4 - 3i
collect like terms
2 - 4i - 35i²
3. Given the expression;
\(\sqrt[3]{81} x^7 y^9z^5\)
Take the cube root of the value, we have;
4x^7y^9z^5
Thus, the expressions are simplified to 3x^3/2/ y , 2 - 4i - 35i² and 4x^7y^9z^5
Learn more about algebraic expressions here:
https://brainly.com/question/4344214
#SPJ1
Find the average value of f(x,y) = x^2y over the rectangle R with vertices (-1,0), (-1,8), (2,8), (2,0)
Answers
Evaluating this integral will give us the average value of the function f(x, y) over the rectangle R.
To find the average value of the function f(x, y) = x^2y over the rectangle R with vertices (-1, 0), (-1, 8), (2, 8), and (2, 0), we need to calculate the double integral of f(x, y) over the region R and divide it by the area of the region.
The area of the rectangle R can be calculated as the product of the length and width:
Area = (2 - (-1)) * (8 - 0) = 3 * 8 = 24
The double integral of f(x, y) over R is:
∬R f(x, y) dA
To calculate this integral, we need to set up the limits of integration for x and y. Since the rectangle R is defined by the given vertices, the limits for x are -1 to 2, and the limits for y are 0 to 8.
Therefore, the average value of f(x, y) over the rectangle R is given by:
Average value = (1/Area) * ∬R f(x, y) dA
Substituting the limits and the function into the integral, we get:
Average value = (1/24) * ∫[0,8] ∫[-1,2] x^2y dx dy
Evaluating this integral will give us the average value of the function f(x, y) over the rectangle R.
Learn more about integral here:
https://brainly.com/question/30094386
#SPJ11
A sequence has its first term equal to 4, and each term of the sequence is obtained by adding 2 to the previous term. If f(n) represents the nth term of the sequence, which of the following recursive functions best defines this sequence? (1 point)
a
f(1) = 2 and f(n) = f(n − 1) + 4; n > 1
b
f(1) = 4 and f(n) = f(n − 1) + 2n; n > 1
c
f(1) = 2 and f(n) = f(n − 1) + 4n; n > 1
d
f(1) = 4 and f(n) = f(n − 1) + 2; n > 1
Answers
Answer:It would be f(n)= f(n-1) +4 this is because f(n-1) means the previous term and you would add your 4 every time you gain.
Step-by-step explanation:
A new tv show will air live at 8pm Eastern Standard Time.
What time will it air in Central Standard Time?
Answers
Answer:
7:00pm
Step-by-step explanation:
Write the linear equation that gives the rule for this table.
x y
1 10
2 5
3 0
4 –5
Write your answer as an equation with y first, followed by an equal's sign.
Answers
The linear equation that gives the rule for this table is y = -5x + 15
How to determine the linear equation?The table of values is given as:
x y
1 10
2 5
3 0
4 –5
On the above table, we can see that:
As x increases by 1, the value of y decreases by 5
This means that the slope is
Slope = -5
Also, the above table can be modified as follows (using the slope of -5)
x y
0 15
1 10
2 5
3 0
4 –5
This means that the y-intercept is
y-intercept = 15
A linear equation is represented as
y = slope * x + y-intercept
So, we have
y = -5x + 15
So, the equarion is y = -5x + 15
Read more about linear equation at
https://brainly.com/question/13738662
#SPJ1
4 × square root of 3
Answers
Please find the photograph for the square root of 3.
Firstly, you have to write 3 as 3. 00 00 00.Then we should find out the root of the perfect square which is less than 3. Here, 1 is the required perfect square root because 1 × 1 = 1 only which is less than 3.Now 3 - 1 = 2 and we are placing 2 zeros after it so that it will be 200. Now we have to add 1 with the divisor 1 which will be 2. Then we have to select a number to be placed beside this 2 in such a way that if we multiply this combined number with the new number, then we will get a number which is less than 200. We see that if we place 7 after 2 and multiply 27 with 7, we get 189 which is less than 200. Now 200 - 189 = 11 and we are placing 2 zeros after it so that it will be 1100. Now we have to add 7 with the divisor 27 which will be 34. Then we have to select a number to be placed beside this 34 in such a way that if we multiply this combined number with the new number, then we will get a number which is less than 1100. We see that if we place 3 after 34 and multiply 3 with 343, we get 1029 which is less than 1100. Now 1100 - 1029 = 71 and we are placing 2 zeros after it so that it will be 7100. Now we have to add 3 with the divisor 343 which will be 346. Then we have to select a number to be placed beside this 346 in such a way that if we multiply this combined number with the new number, then we will get a number which is less than 7100. We see that if we place 2 after 346 and multiply 2 with 3462, we get 6924 which is less than 7100. So, we will get the quotient as 1.732 (corrected to three places of decimal).4√3
= 4 × 1.732
= 6.928
Answer:6.928
Hope it helps

Solve the second-order differential equations with constant coefficients: a. y" - 4y' + 13y = 0 b. y" - 4y' + 4y = 0
Answers
The general solution is: y = c₁e^(2t)cos(3t) + c₂e^(2t)sin(3t) where c₁ and c₂ are arbitrary constants.
To solve the second-order differential equation with constant coefficients y" - 4y' + 13y = 0, we can assume a solution of the form y = e^(rt), where r is a constant to be determined.
Substituting this assumption into the differential equation, we get:
y" - 4y' + 13y = 0
\((e^(rt))" - 4(e^(rt))' + 13(e^(rt)) = 0\)
Differentiating twice with respect to t:
\(r^2 e^(rt) - 4r e^(rt) + 13 e^(rt) = 0\)
Factoring out e^(rt):
\(e^(rt) (r^2 - 4r + 13) = 0\)
For the equation to hold true for all t, the expression in parentheses must be zero:
\(r^2 - 4r + 13 = 0\)
Using the quadratic formula:
r =\((4 ± sqrt((-4)^2 - 4(1)(13))) / (2*1)\)
r = (4 ± sqrt(16 - 52)) / 2
r = (4 ± sqrt(-36)) / 2
r = (4 ± 6i) / 2
r = 2 ± 3i
Since we have complex roots, the general solution is:
y = c₁\(e^(2t)\)cos(3t) + c₂\(e^(2t)\)sin(3t)
where c₁ and c₂ are arbitrary constants.
Learn more about differential here:
https://brainly.com/question/33433874
#SPJ11
help me on both questions as attached below.
Also it's workings on how to get that if possible

Answers
Answer:
a) 160km
b) it will take 3.2 hours or 192 minutes or 3 hours and 12 minutes
Step-by-step explanation:
a) d=speedxtime
so, 64x2. 5=160km
b) time=d/s
so, 160/50
it will take 3.2 hours or 192 minutes or 3 hours and 12 minutes
A local library is on one side of town, and a school is 540,000 centimeters away. The distance from the school to home is 480,000 centimeters. Find the total distance from the library to the school, and from the school to home. Give your answer in centimeters and in scientific notation.
Answers
The total distance from the library to the school is 1,020,000 centimeters (1.02 x 10^6 cm), and the distance from the school to home is 480,000 centimeters (4.8 x 10^5 cm).
To find the total distance from the library to the school, we add the distance from the library to home (unknown) and the distance from home to the school (540,000 cm):
Total distance = Distance from library to home + Distance from home to school
Total distance = x + 540,000 cm
Given that the distance from home to school is 480,000 cm, we can substitute it into the equation:
Total distance = x + 480,000 cm + 540,000 cm
Total distance = x + 1,020,000 cm
Therefore, the total distance from the library to the school is 1,020,000 centimeters (1.02 x 10^6 cm).
Similarly, the distance from the school to home is given as 480,000 centimeters (4.8 x 10^5 cm).
It's important to note that the unknown distance from the library to home is represented by 'x' in this explanation, and its value is not provided in the question.
Learn more about substitution here:
https://brainly.com/question/22340165
#SPJ11
A rectangular prism has a base that is 1.5 meters by 2 meters and the prsim is 4 meters high,What is the surface area
Answers
Answer:
34
Step-by-step explanation:
the equation is 2(lw+lh+wh)
2( 1.5 x 2 + 1.5 x 4 + 2 x 4)
Answer:
Step-by-step explanation:
surface area=2lb+2(l+b)h
=2×1.5×2+2(1.5+2)×4
=6+2×3.5×4
=6+28
=34 sq. m
if p varies inversely as the square root of q, and p=12 when q=36, find p when q=16
Answers
Answer:
Step-by-step explanation:
p = k / sqrt(q)
The first job is to find k.
p = 12
q = 36
Solution for k
12 = k / sqrt(36)
sqrt(36) = +/- 6
Multiply both sides by +/-6
12 * +/- 6 = k
k = +/- 72
Solution for q = 16
p = +/-72/ sqrt(16)
p = +/- 72 / sqrt(16)
p = +/- 72 / +/-4
p = 18
suppose that a married man is selected at random and a married woman is selected at random. find the approximate probability that the woman will be taller than the man.
Answers
The approximate probability that a married woman selected at random is taller than her husband is 8.85%.
We can use the concept of sampling distribution of the difference between two means to approximate the probability that a randomly selected married woman is taller than her husband.
Let X be the height of a married man and Y be the height of a married woman. Then, the probability that a woman is taller than her husband can be expressed as P(Y > X).
The sampling distribution of the difference between two means can be approximated by a normal distribution if the sample sizes are large enough. In this case, since we have a large sample of 400 couples, we can assume that the sampling distribution of the difference in heights between married men and women is approximately normal.
The mean of the difference in heights between married men and women is
65 - 70 = -5 inches
The standard deviation is the
√(3² + 2.5²) = 3.7 inches.
We can then standardize the difference using the formula:
Z = (Y - X - (-5))/3.7
P(Y > X) = P(Z > (0 - (-5))/3.7) = P(Z > 1.35)
Using a standard normal table or calculator, we find that the probability of a woman being taller than her husband is approximately 0.0885 or 8.85%.
To learn more about probability click on,
https://brainly.com/question/14382068
#SPJ4
Complete question is:
A random sample of 400 married couples was selected from a large population of married couples.
Heights of married men are approximately normally distributed with mean 70 inches and standard deviation of 3 inches.
Heights of married women are approximately normally distributed with mean 65 inches and standard deviation 2.5 inches.
There were 20 couples in which the wife was taller than her husband, and there were 380 couples in which the wife was shorter than her husband
suppose that a married man is selected at random and a married woman is selected at random. find the approximate probability that the woman will be taller than the man.

−5x+2y=9
y=7x
for substitution
Answers
The value of x from the equation is 1
The value of y from the equation is 7
How to calculate the value of x and y ?-5x+2y= 9............equation 1
y= 7x...............equation 2
Substitute 7x for y in equation 1
-5x + 2(7x) = 9
-5x + 14x= 9
9x= 9
x= 9/9
x= 1
Substitute 1 for x in equation 2
y= 7x
y= 7(1)
y= 7
Hence the value of x is 1 and the value of y is 7
Read more on equation here
https://brainly.com/question/10716108
#SPJ1
Find the volume of radius 7 cm in diameter of 12 cm in 3.14
Answers
The volume of a sphere with a radius of 7 cm (or diameter of 12 cm) is 904.32 cubic centimeters.
To find the volume of a sphere with a radius of 7 cm, we can use the formula:
V = (4/3) * π * r^3
where V represents the volume and r represents the radius. However, you mentioned that the diameter of the sphere is 12 cm, so we need to adjust the radius accordingly.
The diameter of a sphere is twice the radius, so the radius of this sphere is 12 cm / 2 = 6 cm. Now we can calculate the volume using the formula:
V = (4/3) * π * (6 cm)^3
V = (4/3) * 3.14 * (6 cm)^3
V = (4/3) * 3.14 * 216 cm^3
V = 904.32 cm^3
For more such questions on volume
https://brainly.com/question/463363
#SPJ8
find the mean, median and mode of these numbers: 9, 10, 9, 9, 11, 9, 10, 9, 9, 10 round all answers to the hundreth place.
Answers
The mean median mode of the data 9,10,9,9,11,9,10,9,9,10 is
Mean =9.5
Median = 11 or 9
Mode is 9
Given that,
The data is 9,10,9,9,11,9,10,9,9,10
The data's mean, median, and mode must be determined.
We know that,
The arithmetic mean of the provided data is another name for mean. If the data are grouped and sorted in ascending order, the median is the value that falls in the middle of the set of grouped data. The value that dominates the data is known as the mode. The Mean, Median, and Mode formulas are described independently for the group of data in the sections that follow.
The data is 9,10,9,9,11,9,10,9,9,10
Mean = 9+10+9+9+11+9+10+9+9+10/10 =95/10=9.5
Median = 11 or 9
Mode is 9
Therefore, The mean median mode of the data 9,10,9,9,11,9,10,9,9,10 is
Mean =9.5
Median = 11 or 9
Mode is 9
To learn more about mode visit: https://brainly.com/question/15323584
#SPJ4
Evaluate 1 1/2 + 3/4 ÷ (-1/3) - 2/3 Enter your answer as a mixed number in simplest form in the box
Answers
The result of the expression as a mixed fraction is -1 5/12
Given the expression
\(1\frac{1}{2}+\frac{3}{4}\div (-\frac{1}{3} ) -\frac{2}{3}\)
Write as an improper fraction
\(\frac{3}{2}+\frac{3}{4}\div (-\frac{1}{3} ) -\frac{2}{3}\)
Using the PEDMAS rule;
\(=\frac{3}{2}+(\frac{3}{4}\div (-\frac{1}{3} )) -\frac{2}{3}\\=\frac{3}{2}+(\frac{3}{4}\times -3) -\frac{2}{3}\\=\frac{3}{2}-(\frac{9}{4}) -\frac{2}{3}\\\)
Find the LCM of the result
\(=\frac{18-27-8}{12}\\= \frac{-17}{12}\\= -1\frac{5}{12}\)
Hence the result of the expression as a mixed fraction is -1 5/12
Learn more here ; https://brainly.com/question/1965935