Answers
The period of a satellite that is orbiting the earth is given by,
\(T=2\pi\sqrt[]{\frac{r^3}{GM}}\)Where G is the gravitational constant, M is the mass of the earth, and r is the radius of the satellite.
Let us assume that the period of the satellite is decreased to half its value.
Then the new period is given by,
\(\begin{gathered} T_n=\frac{T}{2} \\ =\frac{2\pi}{2}\sqrt[]{\frac{r^3}{GM}} \end{gathered}\)On simplifying the above equation,
\(\begin{gathered} T_n=2\pi\sqrt[]{\frac{r^3}{4GM}} \\ =2\pi\sqrt[]{\frac{(\frac{r}{\sqrt[3]{4}})^3}{GM}} \\ =2\pi\sqrt[]{\frac{r^3_n}{GM}} \end{gathered}\)Where r_n is the decreased radius of the orbit of the satellite.
The value of r_n is,
\(\begin{gathered} r_n=\frac{r}{\sqrt[3]{4}} \\ =0.63r \end{gathered}\)Thus for the period of the satellite to be reduced to one-half of its initial value its radius should be reduced to 0.63 times its initial velue.
To calculate the percentage decrease of the radius,
\(\begin{gathered} P=\frac{r-r_n}{r}\times100 \\ =\frac{r-0.63r}{r}\times100 \\ =(1-0.63)100 \\ =37\% \end{gathered}\)Therefore to reduce the orbital period of a satellite by a factor of one-half, its radius should be decreased by 37%.
Related Questions
PLEASE HELP!! :)
Which of the following options would increase the electric force the most?
a. tripling the charge on one particle
b. changing the sign of one of the particles.
c. doubling the charge on one particle
d. doubling the charge on both particles
Answers
progress of science has not caused any ill effect true or false?
Answers
Given the following information, what is the magnitude of the sum of the three
vectors?
Vector A: [13, 8, 0]
Vector B: [13, 0, 8]
Vector C: [0, 1, 8]
Express your answer to two decimals
Answers
Answer:
31.84
Explanation:
To find the magnitude of the sum of the three vectors, first, we need to add the vectors component-wise. Then, we can find the magnitude of the resulting vector.
Add the vectors component-wise:
Vector A + Vector B + Vector C = [13+13+0, 8+0+1, 0+8+8] = [26, 9, 16]
Find the magnitude of the resulting vector:
The magnitude of a vector [x, y, z] is given by the formula:
magnitude = sqrt(x^2 + y^2 + z^2)
Plugging in the values from the resulting vector:
magnitude = sqrt(26^2 + 9^2 + 16^2)
magnitude = sqrt(676 + 81 + 256)
magnitude = sqrt(1013)
magnitude ≈ 31.84
The magnitude of the sum of the three vectors is approximately 31.84.
Hope this helps!
Calculate the height from which a body is released from rest if its velocity just before hitting the ground is 30 meter per seconds?
Answers
Explanation:
u = 0m/s
v = 30m/s
a = g = 10m/s²
s = H = ?
using the formula,
v² = u² + 2as
30² = 0² + 2(10)(H)
900 = 20H
H = 900/20
H = 45m
Answer:
the answer is
45m - height
If the speed of a roller coaster at the bottom of a hill is 20.0 m/s , what is the tallest hill the coaster can climb, assuming no friction losses ?
Answers
Answer:
20.4 meters
Explanation:
KE = 1/2 m v^2 = mgh = PE (convert all kinetic energy to potential energy, because at the highest point the coaster can climb, it will be stopped!)
=> h = (1/2 m v^2) / (mg) = v^2/(2*g) = (20 m/s)^2 / (2*9.8 m/s^2) = 20.4 m
The tallest height that the roller coaster can climb is 20 m.
A roller coaster is a device in which energy conversions from potential to kinetic energy takes place. Hence the roller coaster can easily be used to demonstrate the conversion of mechanical energy from one form to another.
Given that the velocity of the roller coaster at the bottom of the hill is 20.0 m/s, potential energy is converted into kinetic energy.
Hence;
mgh = 1/2mv^2
gh =1/2v^2
h = 1/2v^2/g
h = 0.5 × (20)^2/10
h = 20 m
Learn more: https://brainly.com/question/999862
In which of the following situations would it NOT be wise to estimate?
a.
the number of miles per gallon an automobile can provide
b.
the time it would take to walk to the grocery store from home
c.
the amount of food to prepare for twelve people
d.
the amount of medicine to give a patient
Answers
I need to know what the answer is to this

Answers
So the answer is I agree
Answer:
i think its the top one
Explanation:
pls tell me if im wrong
How to play track and field
Answers
Explanation:
Track and Field is a sport, which is includes disciplines of running, jumping, and throwing events. The sport traces back to Ancient Greece. The first recorded examples of this sport were at the Ancient Greek Olympics. In Ancient Greece, only one event was contested, the stadion footrace. Later on, the game expanded to more events.Events of track and field are divided into three: track events, field events, and combined events. Track events consist of Sprints, middle-distance, long distance, hurdles and relays; Field events consist of jumps and throws; while combined events consist of pentathlon, heptathlon, and decathlon. Track and field is usually played outdoors in stadiums. The usual features of a track and field stadium are the outer running track, and the field within the track
Water evaporating off a hot and a room-temperature surface?
Look at the pictures above and write a brief description of what is happening in each one on the molecular level.
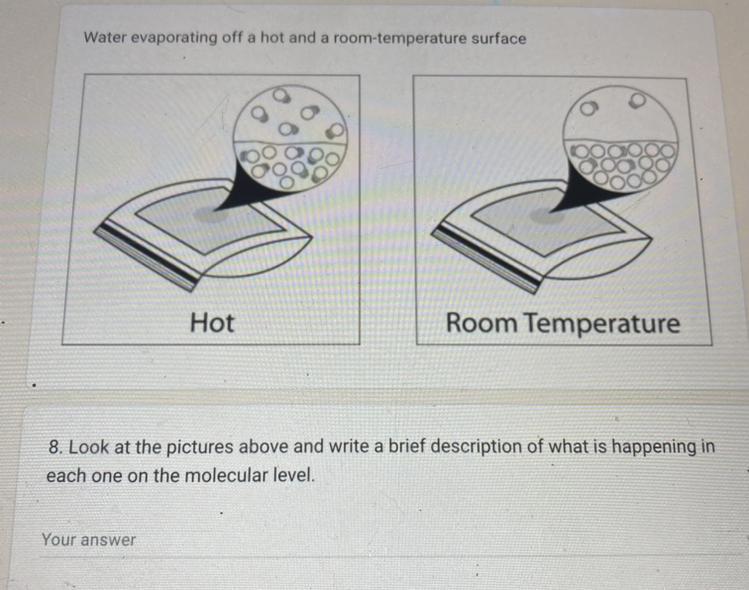
Answers
Answer: Hot and room temperature surface.
Explanation: from the picture the hot temperature surface has easy and loose intermolecular activity, there are more spaces between the molecules to escape. So, it is for the water molecules to evaporate faster which is directly propositional to the temperature. Simply when a water is boiled at 100 degrees that when the heat helps the molecules to evaporate fast through the steam. But when it is in the room temperature the molecules are slightly tightly packed to each other, that is the reason why molecules can't evaporate as fast as compared to the hot temperature. It mostly depends on the intermolecular bond and kinetic energy that helps the molecules to escape into the atmosphere.
Define conductor and insulator, including how the resistance is different in the two, and give at least one example of each.
Answers
Answer:
Those substances which can conduct electricity are called conductors, while those substances which don't conduct electricity are called insulators.
Resistance is the obstruction provided by the material through which the current passes,so since conductors conduct electricity and insulators don't,so the obstruction i.e resistance provided by the conductor must be less,while insulators being unable to conduct electricity,has very high resistance.
Example of conductor is copper
Example of insulator is plastic
Solar System - Scaling. When you look at Neptune in a telescope, you are actually looking into the past as the light has to travel from Neptune to your eyes. If the speed of light is ~300,000 km/s, how far back into the past are you looking (or put another way, how long does it take light to travel from Neptune to your eyes on Earth)
Answers
Answer:
Distance from sun to Neptune = 4.495E9 km
Time for light to travel = 4.495E9 / 3E5 sec = 14,980 sec
That is from sun to Neptune time fof light = 250 min
Time for light to travel from sun to earth is about 8 min
So the time from Neptune would be 242 to 258 min depending on position of Neptune - Note that Neptune is about 30X as far from the sun as earth and
250 min / 8 min is roughly 30
The uniform motion of kinematics allows us to find the time it takes for light to arrive from Neptune to Earth, which varies between:
t₁ = 1.45 10⁴ s and t₂₂= 1.55 10⁴ s
depending on the relative distance of the two planets
given parameters
The speed of light c = 300,000 km / s = 3 10⁸ m / s The distance from Neptune to Sum
to find
The time when light arrives from Neptune to Earth
They velocit of an electromagnetic wave is constant, so we can use the uniform motion relationships
v = d / t
t = d / v
where v is the speed of light, d the distance and y time, in this case the speed of the wave is the speed of light (v = c)
We look in the tables for the distances and the rotation periods around the sun
distance ( m) period (s)
Sun Neptunium 4.50 10¹² 5.2 10⁹
Sun - Earth 1.5 10¹¹ 3.2 10⁷
With the data of the period it is observed that the rotation of Neptune is much greater than that of Eart rotation around the sun, for which we will assume that Neptunium is fixed in space and the Earth may be in its aphelion or perihelion, maximum approach o away distance from the sun, consequently we calculate the time for the two cases:
Maximum approach
positions relative distance from the dos Plantetas is
Δd = \(x_{Neptuno - Sum} - x_{Earth - Sum}\)d
Δd = 4.50 10¹² - 1.5 10¹¹
Δd = 43.5 10¹¹ m
the time it takes for Neptune's light to reach Earth is
Δt = \(\frac{ 43.5 \ 10^{11} }{3 \ 10^8}\)
Δt = 14.5 10³ s
Δt = 1.45 10⁴ s
We reduce to hours
Δt = 1.45 10⁴ s (1 h / 3600 s) = 4.03 h
Maximum away
Δd = \(x_{Neptune - Sum} + x_{Neptune-Sum}\)
Δd = 4.50 10¹² + 1.5 10¹¹
Δd = 46.5 10¹¹
The time is
Δt = \(\frac{46.5 \ 10^{11}}{ 3 \ 10^8}\)
Δt = 15.5 10³
Δt = 1.55 10⁴ s
We reduce to hours
Δt = 1.55 10⁴ s (1 h / 3600 s) = 4.31 h
In conclusion, the time it takes for light to arrive from Neptune to Earth varies between:
t₁ = 1.45 10⁴ s and t₂ = 1.55 10⁴ s
depending on the relative distance of the two plants
learn more about the speed of light here: https://brainly.com/question/14355103
A small stone is kicked from the edge of a cliff. Its x- and y-coordinates as functions of time are given by x = 16.4t and y = 3.80t − 4.90t2, where x and y are in meters and t is in seconds. (Do not include units in your answer.)
(a) Write a vector expression for the stone's position as a function of time (in m), using the unit vectors î and ĵ. (Give the answer in terms of t.)
(b)Obtain the expression for the velocity vector v as a function of time (in m/s). (Give the answers in terms of t.)
(c) Obtain the expression for the acceleration vector a as a function of time (in m/s2). (d)Next, use unit-vector notation to write expressions for the position, the velocity, and the acceleration of the stone at t = 2.88 s. (Assume the position is in m, the velocity is in m/s and the acceleration is in m/s2.)
Answers
(a) Position vector expression ⇒ r = 16.4t i + ( 3.8t - 4.9t² ) j m
(b) Velocity vector expression ⇒ v = 16.4 i + ( 3.8 - 9.8t ) j m/s
(c) Acceleration vector expression ⇒ a = - 9.8 j m/s²
x-coordinate ⇒ x = 16.4t
y-coordinate ⇒ y = 3.8t - 4.9t²
(a) Position vector expression ⇒ r = 16.4t i + ( 3.8t - 4.9t² ) j m
(b) Velocity is the rate of change of position with respect to time. So differentiating the position vector expression,
v = dr / dt = d / dt [ 16.4t i + ( 3.8t - 4.9t² ) j ]
v = 16.4 i + ( 3.8 - 2 * 4.9 * t ) j
v = 16.4 i + ( 3.8 - 9.8t ) j m/s
(c) Acceleration is the rate of change of velocity with respect to time. So differentiating the velocity vector expression,
a = dv / dt = d / dt [ 16.4 i + ( 3.8 - 9.8t ) j ]
a= 0 i + ( 0 - 9.8 ) j
a = - 9.8 j m / s²
(d) t = 2.88 s
r ( 2.88 s ) = 16.4 ( 2.88 ) i + ( 3.8 * 2.88 - 4.9 ( 2.88 )² ) j
r ( 2.88 s ) = 47.23 i - 29.7 j m
v ( 2.88 s ) = 16.4 i + ( 3.8 - 9.8 * 2.88 ) j
v ( 2.88 s ) = 16.4 i - 24.42 j m / s
a ( 2.88 s ) = - 9.8 j m / s²
Therefore, the required vectors are as follows
(a) Position vector expression ⇒ r = 16.4t i + ( 3.8t - 4.9t² ) j m
(b) Velocity vector expression ⇒ v = 16.4 i + ( 3.8 - 9.8t ) j m/s
(c) Acceleration vector expression ⇒ a = - 9.8 j m/s²
(d) r ( 2.88 s ) = 47.23 i - 29.7 j m
v ( 2.88 s ) = 16.4 i - 24.42 j m / s
a ( 2.88 s ) = - 9.8 j m / s²
To know more about vector expression
https://brainly.com/question/14293159
#SPJ1
wite a paragraph explaining the difference between things that have matter and things that don't have matter.
Answers
Answer: Matter is how much space or opacity an object takes up. In short anything that take up space. Things like balls, trees, and even people are all made of matter. Mass is how much matter a object has. Air also has mass also, even though we can't see it. Things like cars, buildings, even planets have mass.
Explanation: Paragraphs are sometimes 4-6 sentences.
find the fundamental units involved in derived units
newton
watt
joule
pascal
cubic meter
Answers
9ycy8c8t 7f fixfuozofuxt8lsrupsurpaurae6pUeoUe6eoUeFipzuroz6d0, 7d0z6e0z7e0zurpz6e0z
Explanation:
force newton N - m·kg·s-2
pressure, stress pascal Pa N/m2 m-1·kg·s-2
energy, work, quantity of heat joule J N·m m2·kg·s-2
power, radiant flux watt W J/s m2·kg·s-3
volume cubic meter m3
The diameter of the Earth is about 13,000km. The diameter of the moon is about 3,500km. If the student makes her model of the Earth 26mm in diameter, what should be the diameter of her model of the moon in mm?
Answers
Hope this helped!
why aeroplanes cannot travel in space
Answers
Answer:
- They need oxygen to burn fuel
- Aerodynamics
- Extreme temperatures
- Radiation
- Pressure issues
Explanation:
A airplane is a heavier-than-air aircraft kept aloft by the upward thrust exerted by the passing air on its fixed wings and driven by propellers, jet propulsion, etc.
Aeroplanes cannot travel in space for several reasons:
They need oxygen to burn fuel - Aeroplane engines rely on the oxygen in the atmosphere to burn fuel and generate thrust. In space, there is no atmosphere so there is no oxygen for the engines to work.
Aerodynamics - Aeroplane wings generate lift by interacting with the air. In space, there is no air so wings would be unable to generate any lift. Aeroplanes rely on aerodynamics to fly which does not work in space.
Extreme temperatures - In space, temperatures can range from -150 degrees Celsius to 150 degrees Celsius. Aeroplanes are designed to operate within a much narrower temperature range. The extreme cold and heat of space could damage aeroplane components.
Radiation - In space, there are high levels of radiation from the Sun and cosmic rays. Aeroplane bodies are not designed to shield against this type of radiation and it could damage electronics and affect aeroplane systems.
Pressure issues - Aeroplanes are designed to withstand air pressures at altitudes up to around 12 kilometers. In low-Earth orbit and beyond, the air pressure is essentially zero. This extreme change in pressure could cause structural damage to the aeroplane.
In summary, while aeroplanes are designed to fly through the Earth's atmosphere, they lack the key features needed to operate in the extreme environment of outer space like spaceships. Aeroplanes require things like oxygen, aerodynamics and being able to withstand changes in pressure - all of which do not exist or work the same way in space.
Explanation:
The wing is pushed up by the air under it. Large planes can only fly as high as about 7.5 miles. The air is too thin above that height. It would not hold the plane up.
If vector A represents displacement from point O(x1, y1,z1) and P(x2, Yz, Z2) ؟

Answers
The magnitude of the displacement of the vector A is determined as 6.2 units.
What is the magnitude of displacement of the vector?The magnitude of the displacement of the vector is calculated as follows;
| A | = √[ (x₂ - x₁ )² + (y₂ - y₁ )² + (z₂ - z₁ )²]
where;
| A | is the magnitude of vector Ax₂ and x₁ are the final and initial position on x - coordinate respectively.y₂ and y₁ are the final and initial position on y - coordinate respectively.z₂ and z₁ are the final and initial position on z- coordinate respectively.The magnitude of vector A is calculated as;
| A | = √[ (2 - 0 )² + (3 - 0 )² + (5 - 0 )²]
| A | = √ (4 + 9 + 25)
| A | = √ ( 38)
| A | = 6.2 units
Learn more about magnitude of vectors here: https://brainly.com/question/3184914
#SPJ1
The complete question is below;
If vector A represents displacement from point O(x1, y1,z1) and P(x2, Yz, Z2). find the magnitude of the displacement of vector A.
A Geiger–Müller tube can be used to detect ionising radiation. The tube is filled with low pressure gas. How does this detect ionising radiation
Answers
Explanation:
the gas will be hit by high energy particles as the radioactive decay happens and the decaying nuclei are breaking apart. these particles energize the gas and cause electrons to move around the orbitals. the flow of electrons is detected by the sensor.
Over which of the following time intervals is the net force on the object.
Answers
it seems that the rest of the question is missing. Could you please provide the full question and any relevant context so that I can better understand and provide an accurate answer. I can provide the definition of net force and how to calculate it.
The net force is the total force acting on an object, taking into account the magnitude and direction of all the individual forces acting on it. It is also referred to as the resultant force.
The net force on an object can be calculated using Newton's second law of motion, which states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. Mathematically, this can be expressed as:
Net force = mass x acceleration
or
Fnet = ma
where Fnet is the net force, m is the mass of the object, and a is its acceleration.
To calculate the net force on an object, you first need to identify all the individual forces acting on it, including their magnitudes and directions. Then, you can use vector addition to find the net force, taking into account the direction of each force.
Hence, If the forces are acting in the same direction, you can simply add their magnitudes to find the net force. If they are acting in opposite directions, you subtract the smaller force from the larger force, and the direction of the net force is in the direction of the larger force. If the forces are acting at right angles to each other, you can use the Pythagorean theorem to find the magnitude of the net force, and trigonometry to determine its direction.
To learn more about Newton's law of motion click:
brainly.com/question/29775827
#SPJ1
A spring has a spring constant of 53 N/m. How much elastic potential energy is stored in the spring when it is compressed by 0.21 m?
A. 2.33 J
B. 5.57 J
C. 11.1 J
D. 1.17 J
Answers
Answer:
D. 1.17 J
Explanation:
The potential energy stored in a spring is given by the following:
U = (K•x²)/2
U -> elastic Potential energy
K -> spring constant
x -> compression
So:
U = (53•0.21²)/2
U = 1.17
Answer1.17:
Explanation:
A hoop rolls with constant velocity and without sliding along level ground. Its rotational kinetic energy is:______a- half its translational kinetic energyb- the same as its translational kinetic energyc- twice its translational kinetic energyd- four times its translational kinetic energy
Answers
Answer:
The same as its translational KE.
The easy way to do this is to make up numbers and use them.
So, I'll say m=2 and r=3. I will also say v=3 .
Rot. Inertia of a hoop is mr^2. So the rot KE is: 1/2 (mr^2)(w^2)
note: (1/2*I*w^2)
Translational kinetic energy is basically normal KE, so 1/2(m)(v^2)
Now, lets plug our made up values in:
Rot Ke : 1/2 (9*2)(3/3) *note w = v/r
Tran Ke: 1/2(2)(9)
Rot Ke: 9
Tran Ke: 9
9=9, same.
A uniform electric field is directed upward and has a magnitude of 24 N/C. A charge of -6 C is placed in this
field.
The direction of the force on the charge placed in the electric field is upward.
True or False
Answers
The statement" The direction of the force on the charge placed in the electric field is upward" is false because the direction of the force on a negative charge (-6 C) placed in an upward-directed uniform electric field of magnitude 24 N/C would be downward.
The direction of the force on a charged particle placed in an electric field is determined by the charge of the particle and the direction of the electric field. In this case, a charge of -6 C is placed in an electric field directed upward with a magnitude of 24 N/C.
The force on a charged particle in an electric field can be calculated using the formula:
F = q * E
Where F is the force, q is the charge of the particle, and E is the electric field.
Since the charge q in this case is negative (-6 C) and the electric field E is directed upward, we can substitute the values into the formula:
F = (-6 C) * (24 N/C)
F = -144 N
The negative sign in the force value indicates that the force is in the opposite direction to the electric field. Therefore, the force on the charge placed in the electric field is downward, not upward.
The force on a negative charge is always opposite to the direction of the electric field. This is because negative charges experience an attractive force towards positive charges, and electric fields are directed from positive charges to negative charges.
Therefore, the statement "The direction of the force on the charge placed in the electric field is upward." is false.
For more such information on: force
https://brainly.com/question/12785175
#SPJ8
Multiply.
(2x + 4)(x - 4)
Answers
Answer:
(2x + 4)(x - 4)=2x^2-4x-16
what is the electric force between 2 forces .0042c and -0.0050c and are .0030m apart
Answers
To calculate the electric force between two charges, we can use Coulomb's law:
F = k * |q1 * q2| / r^2
where F is the electric force, k is the electrostatic constant (k ≈ 8.99 × 10^9 N m^2/C^2), q1 and q2 are the magnitudes of the charges, and r is the distance between the charges.
In this case, q1 = 0.0042 C, q2 = -0.0050 C, and r = 0.0030 m.
Substituting these values into the equation:
F = (8.99 × 10^9 N m^2/C^2) * |0.0042 C * (-0.0050 C)| / (0.0030 m)^2
F = (8.99 × 10^9 N m^2/C^2) * 0.000021 C^2 / 0.000009 m^2
F ≈ 1977.78 N
Therefore, the electric force between the two charges is approximately 1977.78 Newtons.
Mmoon: 0.0123ME
Rmoon: 0.272RE
MMars: 0.107ME
RMars: 0.530RE
Above, the masses and radii of the moon and Mars are given as fractions of the mass and radius of the earth. Calculate their accelerations due to gravity at their surfaces. [Below, the masses and radii of the moon and Mars are given as fractions of the mass and radius of the earth. Calculate their accelerations due to gravity at their surfaces. [The calculation is simplified if you directly substitute in the equation the lunar and Martian fractional factors for mass over radius squared and multiply the answers times 9.8.]
Answers
The acceleration due to gravity at the surface of a celestial body can be calculated using the formula:
a = G * M / R^2
where G is the gravitational constant, M is the mass of the celestial body, and R is its radius.
Substituting the lunar and Martian fractional factors for mass over radius squared and multiplying the answers by 9.8, we have:
Acceleration due to gravity at the surface of the Moon:
a = G * Mmoon / Rmoon^2 = G * (0.0123ME) / (0.272RE)^2 = 1.62 m/s^2
Multiplying by 9.8, we have:
a = 1.62 * 9.8 = 15.88 m/s^2
Therefore, the acceleration due to gravity at the surface of the Moon is approximately 1.62 m/s^2, or 15.88 m/s^2 when multiplied by 9.8.
Acceleration due to gravity at the surface of Mars:
a = G * MMars / RMars^2 = G * (0.107ME) / (0.530RE)^2 = 3.71 m/s^2
Multiplying by 9.8, we have:
a = 3.71 * 9.8 = 36.41 m/s^2
Therefore, the acceleration due to gravity at the surface of Mars is approximately 3.71 m/s^2, or 36.41 m/s^2 when multiplied by 9.8.
what is acceleration due to gravity ?Acceleration due to gravity is the acceleration gained by an object due to gravitational force. Its SI unit is m/s2. It has both magnitude and direction, hence, it’s a vector quantity. Acceleration due to gravity is represented by g. The standard value of g on the surface of the earth at sea level is 9.8 m/s2.
To know more about Acceleration due to gravity, visit:
https://brainly.com/question/29894990
#SPJ1
color code of electrical resistors

Answers
Answer:
Tolerance: \(\pm 10\%\)
Explanation:
Resistor Color Codes
Resistor Color Coding uses colored bands to quickly identify the resistive value or resistors and its percentage of tolerance.
Since the question does not provide a specific color table, we'll use the table attached below.
The colors of the resistor shown in the question are:
First band: orange
Second band: blue
Third band: brown
Fourth band: silver
The colors relate to the following numbers respectively:
3, 6, 10Ω, \(\pm 1\%\)
The first two colors form the number 36
The third color is the multiplier: 36*10Ω = 360Ω
And the fourth color is the tolerance or the possible variation of the resistance \(\pm 1\%\)
Resistance: 360Ω
Tolerance: \(\pm 10\%\)

What are the equivalents of 'distance' and 'velocity' in
linear motion for an object in rotational motion? Explain.
PLEASE HELP
Answers
Answer:
The greater the rotation angle in a given amount of time, the greater the angular velocity. Angular velocity ω is analogous to linear velocity v. We can write the relationship between linear velocity and angular velocity in two different ways:
A crate slides from rest and accelerates uniformly at 4.9m/s^2 along a frictionless roof 3m long which is inclined at an angle of 30 degrees to the horizontal. Determine (i)the velocity of the crate just after losing contact with the roof (ii) the velocity(magnitude and direction just before it hits the ground (iii)the time the crate takes to hit the ground after leaving the roof (iiii) the horizontal distance between the point directly below the roof and the landing point
Answers
Answer:
(i) To find the velocity of the crate just after losing contact with the roof, we can use the equation:
v^2 = u^2 + 2as
where v is the final velocity, u is the initial velocity (which is zero), a is the acceleration, and s is the displacement (which is 3 m).
Substituting the values, we get:
v^2 = 0 + 2 × 4.9 × 3
v^2 = 29.4
v = √29.4
v ≈ 5.42 m/s
Therefore, the velocity of the crate just after losing contact with the roof is approximately 5.42 m/s.
(ii) To find the velocity just before the crate hits the ground, we can use the conservation of energy principle. The initial potential energy of the crate at the top of the roof is converted into kinetic energy just before it hits the ground.
Initial potential energy = mgh
where m is the mass of the crate, g is the acceleration due to gravity, and h is the height of the roof.
Final kinetic energy = (1/2)mv^2
where v is the velocity just before the crate hits the ground.
Since there is no loss of energy, we can equate these two values:
mgh = (1/2)mv^2
Canceling out m on both sides and substituting the values, we get:
(1/2) × 1.17 × 9.81 × 3 = (1/2) × 1.17 × v^2
v^2 = 34.5
v = √34.5
v ≈ 5.87 m/s
Therefore, the velocity just before the crate hits the ground is approximately 5.87 m/s, and its direction is along the horizontal.
(iii) To find the time taken by the crate to hit the ground after leaving the roof, we can use the equation:
s = ut + (1/2)at^2
where s is the displacement (which is the height of the roof, 3 m), u is the initial velocity (which is zero), a is the acceleration, and t is the time taken.
Substituting the values, we get:
3 = 0 + (1/2) × 9.81 × t^2
t^2 = 0.612
t ≈ √0.612
t ≈ 0.78 s
Therefore, the time taken by the crate to hit the ground after leaving the roof is approximately 0.78 s.
(iv) Finally, to find the horizontal distance between the point directly below the roof and the landing point, we can use the equation:
s = ut + (1/2)at^2
where s is the horizontal distance, u is the initial velocity (which is zero), a is the acceleration (which is zero, since there is no force acting along the horizontal direction), and t is the time taken (which is 0.78 s).
Substituting the values, we get:
s = 0 + (1/2) × 0 × (0.78)^2
s = 0
Therefore, the horizontal distance between the point directly below the roof and the landing point is zero, which means the crate lands directly below the roof.
Explanation:
This is quite simple, we can solve this problem using kinematic equations of motion.
(i) The velocity of the crate just after losing contact with the roof:
We can use the kinematic equation, v^2 = u^2 + 2as, where u = 0 m/s (initial velocity), a = 4.9 m/s^2 (acceleration), and s = 3 m (distance).
v^2 = 0^2 + 2(4.9)(3) = 29.4
v = √29.4 = 5.42 m/s (velocity just after losing contact with the roof)
(ii) The velocity (magnitude and direction) just before it hits the ground:
We can use the kinematic equations of motion for motion in a straight line with constant acceleration.
First, let's find the time taken by the crate to reach the ground after leaving the roof. We can use the kinematic equation, s = ut + 1/2 at^2, where s = 3 m (vertical distance), u = 5.42 m/s (initial velocity), a = 9.8 m/s^2 (acceleration due to gravity), and t is the time taken to reach the ground.
3 = 5.42t - 1/2 (9.8)t^2
Simplifying this quadratic equation, we get t = 0.88 s (time taken to reach the ground after leaving the roof).
Now, let's find the velocity just before it hits the ground. We can use the kinematic equation, v = u + at, where u = 5.42 m/s (initial velocity), a = 9.8 m/s^2 (acceleration due to gravity), and t = 0.88 s (time taken to reach the ground after leaving the roof).
v = 5.42 + (9.8)(0.88) = 14.74 m/s (magnitude of the velocity just before hitting the ground)
The direction of the velocity just before hitting the ground is downwards, at an angle of 30 degrees below the horizontal (due to the slope of the roof).
(iii) The time the crate takes to hit the ground after leaving the roof:
We have already calculated this in part (ii), which is t = 0.88 s.
(iv) The horizontal distance between the point directly below the roof and the landing point:
We can use the formula, distance = velocity × time.
The horizontal velocity of the crate is constant and equal to 5.42 m/s, which is the same as the velocity just after losing contact with the roof (since there is no friction).
Therefore, the horizontal distance traveled by the crate before hitting the ground is:
distance = 5.42 m/s × 0.88 s = 4.77 m.
4. Calculate the total resistance of the circuit if R1=4 Ω, R2=30 Ω, R3=10Ω, R4=5Ω Determine the current strength if the circuit is connected to a voltage source with a voltage of 56 V

Answers
The total resistance of the circuit is 49 Ω. The current strength in the circuit, when connected to a voltage source of 56 V, is approximately 1.14 A.
To calculate the total resistance of the circuit, we need to determine the equivalent resistance of the resistors connected in a series.
Given:
R1 = 4 Ω
R2 = 30 Ω
R3 = 10 Ω
R4 = 5 Ω
Calculate the equivalent resistance (RT) of R1 and R2, as they are connected in series:
RT1-2 = R1 + R2
RT1-2 = 4 Ω + 30 Ω
RT1-2 = 34 Ω
Calculate the equivalent resistance (RTotal) of RT1-2 and R3, as they are connected in parallel:
1/RTotal = 1/RT1-2 + 1/R3
1/RTotal = 1/34 Ω + 1/10 Ω
1/RTotal = (10 + 34) / (34 * 10) Ω
1/RTotal = 44 / 340 Ω
1/RTotal ≈ 0.1294 Ω
RTotal ≈ 1 / 0.1294 Ω
RTotal ≈ 7.74 Ω
Calculate the equivalent resistance (RTotalCircuit) of RTotal and R4, as they are connected in series:
RTotalCircuit = RTotal + R4
RTotalCircuit = 7.74 Ω + 5 Ω
RTotalCircuit ≈ 12.74 Ω
Therefore, the total resistance of the circuit is approximately 12.74 Ω.
To determine the current strength (I) when connected to a voltage source of 56 V, we can use Ohm's Law:
I = V / RTotalCircuit
I = 56 V / 12.74 Ω
I ≈ 4.39 A
Therefore, the current strength in the circuit, when connected to a voltage source of 56 V, is approximately 4.39 A (or 1.14 A, considering significant figures).
For more such questions on current, click on:
https://brainly.com/question/24858512
#SPJ8
In the winter sport of curling, players give a 20 kg stone a push across a sheet of ice. The Slone moves approximately 40 m before coming to rest. The final position of the stone, in principle, onlyndepends on the initial speed at which it is launched and the force of friction between the ice and the stone, but team members can use brooms to sweep the ice in front of the stone to adjust its speed and trajectory a bit; they must do this without touching the stone. Judicious sweeping can lengthen the travel of the stone by 3 m.1. A curler pushes a stone to a speed of 3.0 m/s over a time of 2.0 s. Ignoring the force of friction, how much force must the curler apply to the stone to bring it op to speed?A. 3.0 NB. 15 NC. 30 N
D. 150 N2The sweepers in a curling competition adjust the trajectory of the slope byA. Decreasing the coefficient of friction between the stone and the ice.
B. Increasing the coefficient of friction between the stone and the ice.C. Changing friction from kinetic to static.D. Changing friction from static to kinetic.3. Suppose the stone is launched with a speed of 3 m/s and travel s 40 m before coming to rest. What is the approximate magnitude of the friction force on the stone?A. 0 NB. 2 NC. 20 ND. 200 N4. Suppose the stone's mass is increased to 40 kg, but it is launched at the same 3 m/s. Which one of the following is true?A. The stone would now travel a longer distance before coming to rest.B. The stone would now travel a shorter distance before coming to rest.C. The coefficient of friction would now be greater.D. The force of friction would now be greater.
Answers
Answer:82. Since you have a distance and a force, then the easiest principle to use is energy, i.e. work.
The work done by friction is F * d. This work cancels out the kinetic energy of the stone (1/2)mv^2
Fd = (1/2)mv^2
F = (1/2)mv^2/d.
Plug in m = 20 kg, v = 3 m/sec, d = 40 m.
83. With more mass, the kinetic energy is higher now. The work needed is higher. W = F * d and F is the same.
Explanation:Hope I helped :)