Directions: Complete each of the following.
1. Write an algebraic equation to represent each of the statements listed below. Let c = the number of carrots and p = the number of potatoes. (Remember: An equation has an equal sign in it.)
1. There are three times as many carrots as potatoes.
2. There are ten more potatoes than carrots.
2. Write an algebraic equation to represent each of the statements listed below. (Remember: An equation has an equal sign in it.)
1. Fifteen is 12 less than three times a number, n.
2. The difference of 8 and a number n, is 5.
3. Write an algebraic expression to answer each of the following questions. (Remember: An expression does not have an equal sign in it.)
1. A notebook costs $5. How many notebooks can you buy with d dollars?
2. A rose costs $4 more than a carnation. If a rose costs d dollars, how much does a carnation cost?
4. Write an algebraic expression to answer each of the following questions. (Remember: An expression does not have an equal sign in it.)
1. Twenty-four crayons were shared equally among a small group of students in a kindergarten classroom. Let k = the number of kindergarten students in that group. How many crayons did each student receive?
2. Each kindergarten student in a small group was given twenty-four crayons. There were k kindergarten students in that group. How many crayons were given to that group of students?
5. Write an algebraic expression to answer each of the following questions. (Remember: An expression does not have an equal sign in it.)
1. Eleven students from one class and x students from another class joined together at recess to form 4 equal-sized teams. How many students were on each team?
2. There were x students in one class who were organized into four equal-sized groups, named Groups A, B, C, and D. Then one student left Group B. How many students remained in Group B?
Answers
Answer:
1. For the statement "There are three times as many carrots as potatoes," the algebraic equation would be: c = 3p. This equation represents that the number of carrots (c) is three times the number of potatoes (p).
2. For the statement "There are ten more potatoes than carrots," the algebraic equation would be: p = c + 10. This equation represents that the number of potatoes (p) is equal to the number of carrots (c) plus ten.
3. For the statement "Fifteen is 12 less than three times a number, n," the algebraic equation would be: 3n - 12 = 15. This equation represents that three times the number (3n) minus 12 is equal to 15.
4. For the statement "The difference of 8 and a number n is 5," the algebraic equation would be: 8 - n = 5. This equation represents that 8 minus the number (n) is equal to 5.
5. For the question "A notebook costs $5. How many notebooks can you buy with d dollars?" the algebraic expression would be: d/5. This expression represents the division of the amount of money (d) by the cost of a notebook ($5).
6. For the statement "A rose costs $4 more than a carnation. If a rose costs d dollars, how much does a carnation cost?" the algebraic expression would be: d - 4. This expression represents the subtraction of $4 from the cost of a rose (d) to find the cost of a carnation.
7. For the question "Twenty-four crayons were shared equally among a small group of students in a kindergarten classroom. Let k = the number of kindergarten students in that group. How many crayons did each student receive?" the algebraic expression would be: 24/k. This expression represents the division of the total number of crayons (24) by the number of students in the group (k).
8. For the statement "Each kindergarten student in a small group was given twenty-four crayons. There were k kindergarten students in that group. How many crayons were given to that group of students?" the algebraic expression would be: 24 * k. This expression represents the multiplication of 24 crayons by the number of kindergarten students in the group (k).
9. For the question "Eleven students from one class and x students from another class joined together at recess to form 4 equal-sized teams. How many students were on each team?" the algebraic expression would be: (11 + x)/4. This expression represents the addition of the number of students from the two classes (11 + x) divided by the number of teams (4).
10. For the statement "There were x students in one class who were organized into four equal-sized groups, named Groups A, B, C, and D. Then one student left Group B. How many students remained in Group B?" the algebraic expression would be: (x/4) - 1. This expression represents the division of the number of students in the class (x) by the number of groups (4), and then subtracting one to account for the student who left Group B.
Learn more about algebraic equations here:
brainly.com/question/23867556
#SPJ11
Related Questions
Elimination was used to solve a system of equations.
One of the intermediate steps led to the equation 9x = 27.
Which of the following systems could have led to this equation?
O
9x + 2y = 21
-9x - 2y = 21
10x - y = 15
x+y = - 12
7x - 2y = 15
x + y = 6
4x + 3y = 24
-5x - 3y = 3
Answers
The system of equation that could have led to the equation 9x = 27 is
7x - 2y = 15
x + y = 6
The correct option is the third option
7x - 2y = 15
x + y = 6
Solving systems of equationsFrom the question, we are to determine the system that could have led to 9x = 27
1.
9x + 2y = 21
-9x - 2y = 21
Subtracting, we get
9x + 2y = 21
-9x - 2y = 21
-------------------
18x + 4y = 0
2.
10x - y = 15
x + y = - 12
Subtracting, we get
10x - y = 15
x + y = - 12
---------------------
9x -2y = 27
3.
7x - 2y = 15
x + y = 6
Here, multiply the second equation by 2
2 × [x + y = 6]
2x + 2y = 12
Now, add to the first equation
7x - 2y = 15
2x + 2y = 12
------------------
9x = 27
4.
4x + 3y = 24
-5x - 3y = 3
Subtracting, we get
4x + 3y = 24
-5x - 3y = 3
---------------------
9x + 6y = 21
Hence, the system of equation that could have led to the equation 9x = 27 is
7x - 2y = 15
x + y = 6
The correct option is the third option
7x - 2y = 15
x + y = 6
Learn more on Systems of equations here: https://brainly.com/question/12691830
#SPJ1
Samantha has a student loan. The loan amount is $15,000 for 10 years. Her interest rate is 8.25%. How much will Samantha pay each month?
How much will Samantha pay in interest?
Answers
Answer:
The amount paid each month would be 125$
The amount will Samantha pay in interest is $12,375
Step-by-step explanation:
In order to calculate How much will Samantha pay each month we would have to make the following calculation:
loan amount is $15,000 for 10 years
Therefore, amount paid each year would be=$15,000/10=$1,500
Hence, amount paid each month would be=$1,500/12=125$
In order to calculate How much will Samantha pay in interest we would have to make the following calculation:
I=P*r*n
I=$15,000*8.25%*10
I=$12,375
The amount will Samantha pay in interest is $12,375
Answer:
The amount paid each month would be 125$
The amount will Samantha pay in interest is $12,375
Step-by-step explanation:
In order to calculate How much will Samantha pay each month we would have to make the following calculation:
loan amount is $15,000 for 10 years
Therefore, amount paid each year would be=$15,000/10=$1,500
Hence, amount paid each month would be=$1,500/12=125$
In order to calculate How much will Samantha pay in interest we would have to make the following calculation:
I=P*r*n
I=$15,000*8.25%*10
I=$12,375
The amount will Samantha pay in interest is $12,375
I NEED HELP ASAP I WILL GIVE 100 PTS IF YOU HELP ME AND GIVE RIGHT ANSWER AND I NEED EXPLANATION PLS HELP
A student is painting a doghouse like the rectangular prism shown.
A rectangular prism with base dimensions of 8 feet by 6 feet. It has a height of 5 feet.
Part A: Find the total surface area of the doghouse. Show your work. (3 points)
Part B: If one can of paint will cover 50 square feet, how many cans of paint are needed to paint the doghouse? Explain. (Hint: The bottom will not be painted since it will be on the ground.) (1 point)
Answers
Answer:
A: 236 sqaure ft.
B: 4 cans
Step-by-step explanation:
Sure, I can help you with that.
Part A:
The total surface area of a rectangular prism is calculated using the following formula:
Total surface area = 2(lw + wh + lh)
where:
l = lengthw = widthh = heightIn this case, we have:
l = 8 feetw = 6 feeth = 5 feetPlugging these values into the formula, we get:
Total surface area = 2(8*6+6*5+8*5) = 236 square feet
Therefore, the total surface area of the doghouse is 236 square feet.
Part B:
Since the bottom of the doghouse will not be painted, we only need to paint the top, front, back, and two sides.
The total surface area of these sides is 236-6*8 = 188 square feet.
Therefore,
we need 188 ÷ 50 = 3.76 cans of paint to paint the doghouse.
Since we cannot buy 0.76 of a can of paint, we need to buy 4 cans of paint.
Answer:
A) 236 ft²
B) 4 cans of paint
Step-by-step explanation:
Part AThe given diagram (attached) shows the doghouse modelled as a rectangular prism with the following dimensions:
width = 6 ftlength = 8 ftheight = 5 ftThe formula for the total surface area of a rectangular prism is:
\(S.A.=2(wl+hl+hw)\)
where w is the width, l is the length, and h is the height.
To find the total surface area of the doghouse, substitute the given values of w, l and h into the formula:
\(\begin{aligned}\textsf{Total\;surface\;area}&=2(6 \cdot 8+5 \cdot 8+5 \cdot 6)\\&=2(48+40+30)\\&=2(118)\\&=236\; \sf ft^2\end{aligned}\)
Therefore, the total surface area of the doghouse is 236 ft².
\(\hrulefill\)
Part BAs the bottom of the doghouse will not be painted, to find the total surface area to be painted, subtract the area of the base from the total surface area:
\(\begin{aligned}\textsf{Area\;to\;be\;painted}&=\sf Total\;surface\;area-Area\;of\;base\\&=236-(8 \cdot 6)\\&=236-48\\&=188\; \sf ft^2\end{aligned}\)
Therefore, the total surface area to be painted is 188 ft².
If one can of paint will cover 50 ft², to calculate how many cans of paint are needed to paint the doghouse, divide the total surface area to be painted by 50 ft², and round up to the nearest whole number:
\(\begin{aligned}\textsf{Cans\;of\;paint\;needed}&=\sf \dfrac{188\;ft^2}{50\;ft^2}\\\\ &= \sf 3.76\\\\&=\sf 4\;(nearest\;whole\;number)\end{aligned}\)
Therefore, 4 cans of paint are needed to paint the doghouse.
Note: Rounding 3.76 to the nearest whole number means rounding up to 4. However, even if the number of paint cans needed was nearer to 3, e.g. 3.2, we would still need to round up to 4 cans, else we would not have enough paint.

01. Which of the choices below constitutes a simultaneous solution to these equations? ( 2 pts.) (1) 4X+3Y=12 and (2) 2X+4Y=8? 02. What combination of X and Y will yield the optimum for this problem? ( 3 pts.) Maximize Z=$10X+$50Y subject to: (1)3X+4Y≤12 and (2)2X+5Y≤10 03. What combination of X and Y will provide a minimum for this problem? (3pts.) Minimize Z=X+5Y subject to: (1) 4X+3Y≥12 and (2) 2X+5Y≥10
Answers
1. The simultaneous solution of the given equations is X=12/5 and Y=4/5
2.1)The combination of X and Y that will yield the optimum for this problem is X=0 and Y=3.3.
2)The combination of X and Y that will provide a minimum for this problem is X=3 and Y=0.
To find the simultaneous solution of the given equations 4X+3Y=12 and 2X+4Y=8, we can use the method of elimination, also known as the addition method. Multiplying the second equation by 2, we get 4X+8Y=16.
Now, we can subtract the first equation from the second equation: 4X+8Y - (4X+3Y) = 8Y - 3Y = 5Y and 16 - 12 = 4. Thus, 5Y=4 or Y = 4/5.
Substituting this value of Y in any of the two equations, we can find the value of X. Let's substitute this value of Y in the first equation: 4X+3(4/5)=12 or 4X
= 12 - (12/5)
= (60-12)/5
= 48/5.
Thus, X = 12/5. Hence, the simultaneous solution of the given equations is X=12/5 and Y=4/5.2. To find the optimal values of X and Y that will maximize the objective function Z=$10X+$50Y, we need to use the method of linear programming.
First, let's plot the feasible region defined by the given constraints:We can see that the feasible region is bounded by the lines 3X+4Y=12, 2X+5Y=10, X=0, and Y=0.
To find the optimal solution, we need to evaluate the objective function at each of the corner points of the feasible region, and choose the one that gives the maximum value.
Let's denote the corner points as A, B, C, and D, as shown above. The coordinates of these points are: A=(0,3), B=(2,1), C=(5/2,0), and D=(0,0). Now, let's evaluate the objective function Z=$10X+$50Y at each of these points:
Z(A)=$10(0)+$50(3)
=$150, Z(B)
=$10(2)+$50(1)
=$70, Z(C)
=$10(5/2)+$50(0)
=$25, Z(D)
=$10(0)+$50(0)=0.
Thus, we can see that the maximum value of Z is obtained at point A, where X=0 and Y=3. Therefore, the combination of X and Y that will yield the optimum for this problem is X=0 and Y=3.3.
To find the combination of X and Y that will provide a minimum for the problem Minimize Z=X+5Y subject to: 4X+3Y≥12 and 2X+5Y≥10, we need to use the same method of linear programming as above.
First, let's plot the feasible region defined by the given constraints:We can see that the feasible region is bounded by the lines 4X+3Y=12, 2X+5Y=10, X=0, and Y=0.
To find the optimal solution, we need to evaluate the objective function Z=X+5Y at each of the corner points of the feasible region, and choose the one that gives the minimum value.
Let's denote the corner points as A, B, C, and D, as shown above.
The coordinates of these points are: A=(3,0), B=(5,1), C=(0,4), and D=(0,0).
Now, let's evaluate the objective function Z=X+5Y at each of these points:
Z(A)=3+5(0)=3,
Z(B)=5+5(1)=10,
Z(C)=0+5(4)=20,
Z(D)=0+5(0)=0.
Thus, we can see that the minimum value of Z is obtained at point A, where X=3 and Y=0. Therefore, the combination of X and Y that will provide a minimum for this problem is X=3 and Y=0.
Know more about equations here:
https://brainly.com/question/25976025
#SPJ8
Solve the equation. Check your solution, if possible.
1 .-26d = -364
2. X - ⅓ = ⅖
3. 4π s + 5π
4. 1.5y + 1.5y + 10 = 4
5. 4(3 - 6a) = 36
6. 4(2g - 3) = 5 (g - 2)
7. 6r - 8 = 8 + 6r
8. 3y + 6 = 3(y + 9)
9. 0.4(15p + 6) = 1.5(4p + 1.6)
10. 9n - 4 + n = 5 + 10n
Solve the equation for y:
11. 24 = 8x + 4y
12. -2x + 2y = 14
13. 2.7 = y - 8.1x
14. ⅓ x + y = 3
15.
Solve A = bh/2 for h.
Find h for the given triangle.
Solve the formula for the bold variable:
16. i = ec
3
17. P = 2l + 2w
18. I = V
R
19. S = p - 7t
Write and solve an equation to find the value of x.
20.
22. The cost of your new book bag is $11.50 more than the cost c of your old book bag. You pay $47 for your new book bag. Write and solve an equation to find the cost of your old book bag.
23. You can rent a video game for $3.50. Your total cost of rentals for the month was $31.50. Write and solve an equation to find the number of video game rentals for the month.
24. You purchase 5 movies and a CD. The cost of the CD is $8.50. Your total bill before tax is $38.45. Write and solve an equation to find the cost of a movie.
Answers
THIS IS URGENT AM I CORRECT PLEASE HALP!!!!!!

Answers
Answer: The answer is 32.
Step-by-step explanation: Yes since you did 9.5+13.6+5.7+3.2 is 32.00 or 32.
when comparing the means of samples from two normally distributed populations that the samples are independent and the population variances are known a z test can be used
Answers
When comparing the means of samples from two normally distributed populations, with independent samples and known population variances, a z-test can be used.
The z-test is a statistical test used to compare means when certain assumptions are met. In this case, the populations from which the samples are drawn are assumed to be normally distributed. The samples being compared should be independent of each other, meaning that the values in one sample are not related to or influenced by the values in the other sample. Additionally, it is assumed that the population variances are known, which is not always the case in practice.
The z-test relies on the calculation of a test statistic called the z-score, which measures the difference between the sample means in terms of standard deviations. The z-score is calculated by subtracting the mean of one sample from the mean of the other sample, and then dividing by the standard deviation of the sampling distribution of the difference in means. The resulting z-score is compared to a critical value from the standard normal distribution to determine the statistical significance of the difference between the means.
If the absolute value of the z-score exceeds the critical value, it indicates that the difference between the sample means is statistically significant, suggesting that the population means are likely to be different. On the other hand, if the z-score is not statistically significant, it suggests that the difference between the sample means may be due to chance, and there is not enough evidence to conclude that the population means are different.
Overall, when comparing the means of samples from normally distributed populations with known variances and independent samples, a z-test provides a way to assess the statistical significance of the difference between the means.
Learn more about z-test here:
https://brainly.com/question/30109604
#SPJ11
f(x)=5x^2-1 If the graph of f is translated vertically downward by 5 units, it becomes the graph of a function h.
Find the expression for h(x)
Answers
Answer:
h(x) = 5x²-6
Step-by-step explanation:
f(x) = 5x²-1, translated vertically downward by 5 units, it becomes
h(x) = 5x² -1-5 = 5x²-6

simplify the following
a.) 2^7 x 2
Answers
Answer:
256
Step-by-step explanation:
i think it is 256.i hope it was that
Answer:
Step-by-step explanation:
Here you go mate;
STEP 1
2^7 x 2 equation
STEP 2
2^7 x 2 simplify
(2^7)(x^2)
STEP 3
128^2 multiply
answer
16384
Fill in the blank in the given sentence with the vocabulary term that best completes the sentence.
A _____ is a flat surface made up of points that extends infinitely in all directions.
Answers
A plane is a flat surface made up of points that extends infinitely in all directions.
What is a plane in mathematics?In mathematics, a plane is a fundamental geometric concept. It is a two-dimensional flat surface that extends infinitely in all directions. A plane can be visualized as a flat sheet or a tabletop. It has length and width but no thickness.
A plane is defined by three non-collinear points or by a linear equation in three variables. The equation of a plane in three-dimensional space is typically written as Ax + By + Cz + D = 0, where A, B, C are coefficients representing the plane's orientation, and D is a constant term.
Planes are important in various branches of mathematics, such as geometry, linear algebra, and calculus. They serve as a foundation for understanding concepts like lines, angles, and shapes in two dimensions. Additionally, planes are used in vector operations, linear transformations, and solving systems of linear equations.
Learn more about: extends infinitely
brainly.com/question/27341447
#SPJ11
Find the value of x.

Answers
Answer:
x=15
Step-by-step explanation:
You can set up the equation like this
60 =3x+15
Get x by itself
45=3x
Divide both sides by 3
x=15
express 60 as a fraction of 3
Answers
Answer:3/5
Step-by-step explanation:
A longitudinal wave produced on a toy slinky travels at a speed of 30 m/s with a frequency of 20 Hz. Find the minimum separation between the consecutive compressions of the slinky.
Answers
Answer:
pagal
Step-by-step explanation:
pagal pagal pagal pagal pagal pagal pagal pagal pagal pagal pagal pagal pagal pagalwhat is the meaning of a mad person
in testing a new drug, researchers found that 5% of all patients using it will have a mild side effect. a random sample of 5 patients using the drug is selected. find the probability that exactly two will have this mild side effect.
Answers
The probability that exactly two will have this mild side effect is
\(P(X=2)=0.1229\)
Probability is defined as the likelihood that a trial will succeed or fail. The ratio of positive events to all possible outcomes is known as probability. The probability scale ranges from 0 to 1.
Given data:
The probability of all patients that will have the mild side effect is p=5%=0.05
The number of people selected is n=14
The expression for the probability that exactly two will have this mild side effect is given as,
\(P(X=x)=^{n}C _{x} p^{x} (1-p)^{n-x}\)
Substituting the values in the above equation as
\(P(X=x)=^{n}C _{x} p^{x} (1-p)^{n-x}\\P(X=2)=^{14}C _{2} 0.05^{2} (1-0.05)^{14-2}\\P(X=2)=91*0.0025*0.54036\\P(X=2)=0.1229\)
Thus the probability that exactly two will have this mild side effect is
\(P(X=2)=0.1229\)
To know more about probability visit: brainly.com/question/11234923
#SPJ4
what is a real number

Answers
Answer:
pi, 7, and 8
Step-by-step explanation:
Nearly any number you can think of is a Real Number
Find the Slope
of the equation that
passes through (4,9)and (-1,-6).
Answers
Answer:
Step-by-step explanation:
Slope = (-6-9)/(-1-4) = -15/-5 = 3
Answer:
\(m=3\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra Iu
Slope Formula: \(m=\frac{y_2-y_1}{x_2-x_1}\)Step-by-step explanation:
Step 1: Define
Point (4, 9)
Point (-1, -6)
Step 2: Find slope m
Simply plug in the 2 coordinates into the slope formula to find slope m
Substitute [SF]: \(m=\frac{-6-9}{-1-4}\)Subtract: \(m=\frac{-15}{-5}\)Divide: \(m=3\)If you rent a car, you have the following options
1. return in with a full gas tank
2. return it without filling at and pay $5.45/ gallon
3. accept a fixed price of $50 fro gasoline
You expect this car to get 28 miles per gallon. The car has a 16 -gallon tank Current gas price is $3.95/gal. What choice should you make if you expect to 150 miles? Solution:
1. Total gasoline consumed gallons;
2. Option 1 cost: __dollars;
3. Option 2 cost: __dollars;
4. Option 3 cost: __dollars;
Answers
If you rent a car, you should choose Option 3 and accept the fixed price of $50 for gasoline if you expect to drive 150 miles.
1. Total gasoline consumed (gallons):
To calculate the total gasoline consumed, divide the expected distance by the car's fuel efficiency:
Total gasoline consumed = Distance / Fuel efficiency
Total gasoline consumed = 150 miles / 28 miles per gallon
Total gasoline consumed ≈ 5.36 gallons
2. Option 1 cost:
In Option 1, you need to return the car with a full gas tank. Since the car has a 16-gallon tank and you've consumed approximately 5.36 gallons, you need to fill up the remaining 16 - 5.36 = 10.64 gallons.
Option 1 cost = 10.64 gallons * $3.95 per gallon = $42.01
3. Option 2 cost:
In Option 2, you return the car without filling it up and pay $5.45 per gallon. As calculated before, you've consumed approximately 5.36 gallons.
Option 2 cost = 5.36 gallons * $5.45 per gallon = $29.20
4. Option 3 cost:
In Option 3, you accept the fixed price of $50 for gasoline. This fixed price is the most cost-effective option compared to the other two choices.
Therefore, the best choice is Option 3, accepting the fixed price of $50 for gasoline, as it offers a better value for the expected distance of 150 miles.
To know more about fuel efficiency calculations, refer here:
https://brainly.com/question/28314501#
#SPJ11
a group of 8 people are ordering pizza. Each person wants 3 slices and each pizza has 10 slices how many pizzas should they order
Answers
Answer:
3
Step-by-step explanation:
8 people
3 slices per person
8 × 3 = 24
They need 24 slices.
1 pizza has 10 slices.
24/10 = 2.4
They need 2.4 pizzas. Since they need to order a whole number of pizzas, they need to order 3 pizzas.
Answer: 3
The perimeter of a square is 128cm the side length of the square is four times a number what is the side length
Answers
Answer:
32cm
Step-by-step explanation:
A square has 4 sides that MUST be equal
In knowing this, you only need to divide the total amount of sides (4) by the perimeter.
\(128 \div 4 = 32\)
Which of the following represents a Hardy-Weinberg equation that has been modified to model the effect of natural selection on a population?
a. p2+ q2+ r2+ 2pq + 2pr + 2qr = 1
b. p2+ 2pq + q2= 2
c. (p-3s)2+ 2(p-s)q + q2= 1
d. p4 + 2p2q2 + q4= 1
Answers
Option C represents a modified Hardy-Weinberg equation that incorporates the effects of natural selection on a population. The equation is given as:
$(p-3s)^2 + 2(p-s)q + q^2 = 1$
In this equation, various terms are included to express the impact of natural selection. Let's break down the equation and understand its components.
$p$ represents the frequency of the dominant allele in the population, while $q$ represents the frequency of the recessive allele. These frequencies are determined based on the initial allele frequencies in the population.
The term $(p-3s)^2$ represents the expected frequency of the homozygous dominant genotype in the next generation. The factor $3s$ denotes the selection coefficient, where $s$ represents the frequency of homozygous recessive individuals who do not survive due to natural selection. By subtracting $3s$ from $p$, we account for the reduction in the frequency of the dominant allele due to selection.
The term $2(p-s)q$ represents the expected frequency of the heterozygous genotype in the next generation. This term incorporates both the initial frequency of the heterozygous individuals, represented by $(p-s)$, as well as the transmission of alleles through reproduction, given by $q$. The factor of 2 accounts for the two possible combinations of alleles in the heterozygous genotype.
Finally, $q^2$ represents the expected frequency of the homozygous recessive genotype in the next generation. This term considers the transmission of the recessive allele, represented by $q$, and its squared value accounts for the homozygous recessive genotype.
The equation is set equal to 1, as the frequencies of all genotypes should sum to 1 in a population.
To know more about Hardy-Weinberg equation
https://brainly.com/question/5028378
SPJ11#
A gift shop uses two sizes of boxes for presents. These boxes have exactly the same shape. The smaller box is 24 cm long, and the larger box is 28 cm long. If 936 cm^2 of wrapping paper is needed to cover the small box how much wrapping paper is needed to cover the largest box?
Answers
Answer:
1,092 cm²
Step-by-step explanation:
Smaller box:
Length = 24 cm
Wrapping paper = 936 cm²
Bigger box:
Length= 28 cm
Wrapping paper = x cm²
Box : wrapping paper = 24 cm : 936 cm²
Box : wrapping paper = 28 cm : x cm²
Equate both ratios to find x
24 : 936 = 28 : x
24/936 = 28/x
Cross product
24 * x = 936 * 28
24x = 26,208
x = 26,208 / 24
x = 1,092 cm²
Bigger box:
Length= 28 cm
Wrapping paper = 1,092 cm²
6/9 x 3/8 in simplest form
Answers
refer the attachment for your answer !!
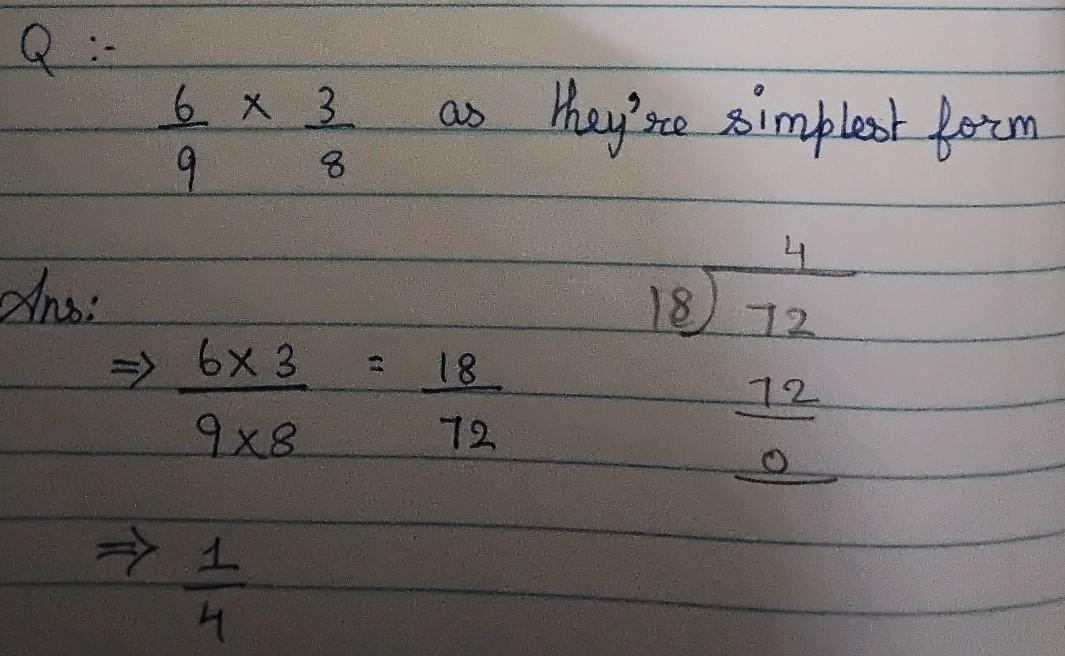
The numbers $1,$ $2,$ $\dots,$ $10$ are to be entered into the 10 boxes shown below, so that each number is used exactly once: \[P = (\square + \square + \square + \square + \square)(\square + \square + \square + \square + \square).\]What is the maximum value of $P$? What is the minimum value of $P$?
Answers
Hint
If we define x to be the value of one of the factors, since 1 + 2 + 3 + 4 + 5 ... + 10 = 11(5) = 55, the value of the other factor has to be 55-x.
To maximize P, you'd like to make x as close as possible to the vertex you found. What if you want to minimize P? Remember x must be an integer.
I hope this helps :)
Need help ASAP. Need to know how to get x and y from x-2y=-13 and y=-2x-6. Not seperate, the xy for both combined if that makes sense. One answer.
Answers
Answer:
\(x = -5\\y = 4\)
Step-by-step explanation:
Not sure I understand that part of your question ...not separate, the xy for both combined.
Here are the solution steps to determine x and y values
Given equations are
\(\begin{amatrix}x-2y=-13 \dots [1] \\\\ y=-2x-6\dots\dots[2]\end{amatrix}\)
In equation [2] get all the variables to the left side and the constant on ther right side:
Add 2x to both sides of the equation:\(y + 2x = 2x - 2x - 6\)Simplify:
\(y + 2x = - 6\)Rewrite:
\(2x+y=-6\dots\dots [3]\)
Let's examine equations [1] and [3]:
\(\begin{aligned}x - 2y &= - 13 \dots [1]\\ 2x + y &= -6\;\;\dots[3]\\\end{aligned}\)
Multiply eq [1], \(x - 2y = -13\) throughout by \(2\):
\(2(x - 2y) &= 2(- 13) \implies 2x - 4y = -26 \dots[4]\\\)
Subtract the equations:
\(2x+y=-6\\-\\\underline{2x-4y=-26}\\\\5y=20\\\\y = \dfrac{20}{5} = 4\)
\(\mathrm{For\:}2x-4y=-26\mathrm{\:plug\:in\:}y=4\):
\(2x-4\cdot \:4=-26\:\\\\2x - 16 = -26\\\\2x = -26 + 16\\\\2x = -10\\\\x = -10/2 = -5\)
when performing a hypothesis test on μ when σ is known, h0 can never be rejected if
Answers
When performing a hypothesis test on the population mean (μ) when the population standard deviation (σ) is known, the null hypothesis (H0) can never be rejected if the sample mean falls within the acceptance range determined by the chosen significance level and the critical values.
In hypothesis testing for the population mean when the population standard deviation is known, the null hypothesis (H0) represents the claim or assumption that the population mean is equal to a specific value. The alternative hypothesis (Ha) states that the population mean is not equal to the specific value.
To determine whether to reject or fail to reject the null hypothesis, we compare the sample mean to the expected value under the null hypothesis. If the sample mean falls within the acceptance range determined by the chosen significance level and the critical values, we do not have sufficient evidence to reject the null hypothesis. The acceptance range is defined by the margin of error around the expected value, and it indicates the range of values that can be considered reasonably close to the expected value.
To know more about hypothesis test,
https://brainly.com/question/29540386
#SPJ11
Use the given data to find the minimum sample size required to estimate the population proportion.
Margin of error: 0.04; confidence level : 99%; from a prior study, p hat is estimated by 0.07.
Answers
To find the minimum sample size required to estimate the population proportion, we'll use the following formula:
n = (Z^2 * p_hat * (1 - p_hat)) / E^2
where:
n = minimum sample size
Z = Z-score, which corresponds to the desired confidence level (99% in this case)
p_hat = estimated population proportion (0.07)
E = margin of error (0.04)
First, we need to find the Z-score for a 99% confidence level. You can find this value using a standard normal distribution table or a calculator. For a 99% confidence level, the Z-score is approximately 2.576.
Now, we can plug the values into the formula:
n = (2.576^2 * 0.07 * (1 - 0.07)) / 0.04^2
n = (6.635776 * 0.07 * 0.93) / 0.0016
n = 0.464507328 / 0.0016
n = 290.316955
Since we cannot have a fraction of a participant, we round up to the nearest whole number to ensure the desired margin of error and confidence level are met.
Minimum sample size (n) = 291
Learn more about it here:
https://brainly.com/question/31581872
#SPJ11
Simplify completely 25 w to the sixth power over 10 w to the third power divided by 30 w squared over 5 w
Answers
Answer:
5w^2 over 12 is your answer. hope it helped!
Step-by-step explanation:
Answer:
5w^2 over 12
Step-by-step explanation:
Help me please I am stuck

Answers
Area of Shaped block is ~
\(118.5 \: {m}^{2} \)\( \huge \boxed{ \mathfrak{Explanation}}\)
The given figure is formed by cutting down a triangular part from a rectangle.
So, Area of figure is equal to ~
Area of Rectangle - Area of Trianglenow, let's find the Area of rectangle as well as Triangle.
Area of rectangle :
\(length \: \times width\)\(13 \times 11\)\(143 \: {m}^{2} \)Now, it's time to find Area of Triangle ~
height = 11 - 4 = 7 m base = 13 - 6 = 7 mSo, Area of Triangle is equal to ~
\( \dfrac{1}{2} \times base \times height\)\( \dfrac{1}{2} \times 7 \times 7\)\( \dfrac{49}{2} \)\(24.5 \: {m}^{2} \)Area of figure is equal to ~
\(143 - 24.5\)\(1 18.5 \: m {}^{2} \)Which choice is a correct equation for the line graphed below?

Answers
Answer:
Step-by-step explanation:
We will work to fill in the slope-intercept form of a line to get the answer to this. y = mx + b. The thing you need to understand first is how to get from one point to another on the line to determine the slope. Look to where the line goes through a corner of one of the squares on the graph. For example, locate these points to see what I mean: (-1, -2), (-2, -5), (1, 4), (2, 7). At each of those points, the line goes through perfectly right where the corners of the squares meet. If you understand this, then you are ready to write the equation of any line.
First locate the y-intercept. This is the point where the line goes through the y-axis. Our line goes through at a y value of +1. So our b value is +1. We will begin by filling that in first:
y = ___x + 1.
Now from that point, you can either go up and to the right to get to another point on the line, or you can go down and to the left. Let's do it both ways so you can see that regardless of which way you pick to go, you'll get the exact same equation every time.
I will go from the y-intercept to the point (1, 4). To get from the y-intercept, I have to go up 3 units til I'm even with the next point on the line, and then to the right 1. So my slope is +3/+1 which is 3.
If I want to go from the y-intercept to the point (-1, -2), I will go down 3 til I'm even with the point, then to the left 1. So my slope will be -3/-1 which is also a positive 3. Fill that in to the slope formula now:
y = 3x + 1, choice A.
Calculate the area of triangle cde with altitude ef, given c (3, −2), d (−1, 2), e (2, 3), and f (0, 1). 4 square units 6.2 square units 8 square units 8.7 square units
Answers
The area of triangle cde with altitude ef is 8 square units. This is calculated by finding the height from point "e" to "f", and the base from point "c" to "d", and then using the formula: Area = (base * height) / 2. The answer is 8 square units.
The area of a triangle can be calculated using the formula:
Area = (Base x Height) / 2
To find the height, we need to find the distance between the point where the altitude intersects the base (in this case, point "f" on the y-coordinate of point "e"), and the other two points of the triangle (in this case, "c" and "d").
The equation for a line in the form y = mx + b can be used to find the y-coordinate of point "f". Using the coordinates of points "c" and "e", the slope can be found by:
m = (3 - (-2)) / (2 - 3) = -1
The y-intercept can be found using the coordinates of point "c" and the slope:
b = -2 - (3 * -1) = 1
So the equation of the line that passes through points "c" and "e" is:
y = -x + 1
We can now use this equation to find the y-coordinate of point "f":
y = -x + 1
y = -0 + 1
y = 1
The height of the triangle is now the distance between points "e" and "f":
height = |3 - 1| = 2
The base of the triangle can be found by taking the distance between points "c" and "d":
base = |(-1) - (3)| = 4
So the area of the triangle is:
Area = (base * height) / 2
Area = (4 * 2) / 2
Area = 8
The area of the triangle is 8 square units.
To learn more about triangle CDE please click on below link.
https://brainly.com/question/28351296
#SPJ4