En un examen muy difícil de universidad, se obliga al profesor a aprobar al menos al 10%.
Calcular la nota a partir de la cual está obligado a aprobar siendo las notas (notas de 0 a 20): 0,
4, 1, 0, 0, 7, 2, 1, 4, 0, 3, 9, 2, 0, 0, 4, 8, 1, 0,9,4
Answers
9 es la nota minima (para aprobar) máxima tal que almenos el 10% de la clase apruebe el examen.
¿A partir de cual nota está obligado a aprobar?Hay 20 estudiantes, y un 10% debe aprobar el examen, es decir, almenos 2 estudiantes deben aprobar el examen.
Las notas de los 20 estudantes son:
{0, 4, 1, 0, 0, 7, 2, 1, 4, 0, 3, 9, 2, 0, 0, 4, 8, 1, 0, 9, 4}
Vemos que hay 2 estudiantes con la nota 9.
Esto significa que si el profesor define que la nota minima para aprobar el examen es 9, entonces dos estudiantes (el 10% de la clase) aprobaría el examen.
Entonces definimos 9 como la nota máxima tal que almenos el 10% de la clase apruebe el examen. (A medida que el valor de la nota decrese, el porcentaje de estudiantes aprobados incrementara).
Sí quieres aprender más sobre porcentajes:
https://brainly.com/question/24554492
#SPJ1
Related Questions
Convert 40 miles per hour to feet per second.
Answers
Answer:
Step-by-step explanation:
58.6667
Answer:
The answer is 58.6667
what is this?????????????????????????????

Answers
which equation, in slope-intercept form, matches the equation shown?A) y = -4/7x + 1B) y = 4/7x - 4 C) y = 5/6x + 1 D) y = -5/6x - 4
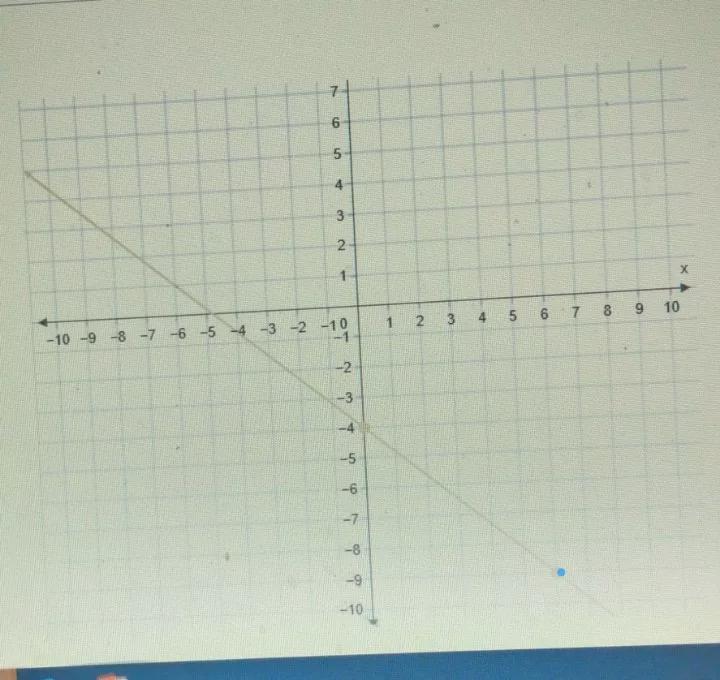
Answers
Okay, here we have this:
We need to find the equation of the line corresponding ti the graph,
First let's calculate the slope using the points (0,-4), (6,-9):
m=(-9-(-4))/(6-0)
m=(-9+4)/6
m=-5/6
And we can see in the graph that the y intercept is b=-4
So, replacing in the equation form we obtain:
y=mx+b
y=-5/6+(-4)
y=-5/6-4
Finally we obtain that the correct answer is the option D.
Find the area of the right triangle.

Answers
Answer:
area is 28 units²
Step-by-step explanation:
find the area of the rectangle with sides 7 and 8 and divide it in half
A=7*8/2= 56/2=28
help me answer this please

Answers
Answer:
3,952 ft
Step-by-step explanation:
Use the sine function since you need to find the hypotenuse but know the opposite side of the angle, since sine is equal to opposite/hypotenuse.
sin8°=\(\frac{550}{c}\)
csin8°=550
c=550/sin8°
c= 3,952
Jaxson drove 4 miles in 1/15of an hour. If he drove at a constant rate, how far did he travel in one hour?
Answers
Answer:
the answer is 60miles
Step-by-step explanation:
because 15*4=60
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment

15 / 35 Marks
66%
The point (-1, 3) is the turning point of the graph with equation y = x2 + ax + b,
where a and b are integers.
Find the values of a and b.
+
Answers
Answer:
y-(x+1)^2-3
Step-by-step explanation:
a=0
b=-3
you would only change a from 0 if you need to change the slope of the graph.
Three white balls and three black balls are distributed in two urns in such a way that each contain three balls. We say that the system is in state i, i=0,1,2,3, if the first urn contains i white balls. At each step, we draw one ball from each urn and place the ball drawn from the first urn into the second, and conversely with the ball from the second urn. Let Xn denote the state of the system after the nth step. Explain why {Xn, n=0 ,1, 2} is a Markov chain and calculate its transition probability matrix.
Answers
Answer:
Following are the answer to this question:
Step-by-step explanation:
In-state 0, it has urns of the 100% chance of shifting towards state 1 because a colored ball must be substituted.
In the \(state 1: \frac{1 \ white}{2 \ black} \ \ \ and \ \ \frac{2 \ white}{1 \ black}\)
The probability to select White from both the probability to select Black from both are 2/9, therefore there are 4/9 possibilities to remain in State 1.
It is probable which white from both the beginning is selected and black from the second, so that 1/9 probability of 0.
The probability is 4/9 that the first black and the second white will be chosen and 4/9 possibility will be made to state 2.
In the \(state 2: \frac{2 \ white}{1 \ black} \ \ \ and \ \ \frac{1 \ white}{2 \ black}\)
This is essentially a state 1 mirror image because identical claims are used for reverse colors.
In-State 3, the urns are 100% likely to revert to State 2.
It is the representation of matrix M is, therefore:
\(( ..0. ..1. ..0. ..0. )\\\\( \frac{1}{9} \frac{4}{9} \frac{4}{9}.. 0. )\\\\( ..0. \ \frac{4}{9} \ \frac{4}{9} \ \frac{1}{9})\\\\( ..0. ..0. ..1. ..0. )\\\\So, \\ X_n = M \times X_{n}-1 \\\\Or\\X_n = M^n \times X_0\)
Monthly deposits of $480 were made at the end of each month for eight years. If interest is 4.5% compounded semi-annually, what amount can be withdrawn immediately after the last deposit?
Answers
The amount that can be withdrawn immediately after the last deposit is approximately $8,876.80.
To solve this problemWe can use the formula for the future value of an ordinary annuity. The formula is given by:
\(FV = P * [(1 + r/n)^(^n^t^) - 1] / (r/n)\)
Where
Future value is represented by FVmonthly deposit amount by Pannual interest rate by rnumber of compounding periods by n years by tGiven:
P = $480 (monthly deposit)r = 4.5% = 0.045 (annual interest rate)n = 2 (compounded semi-annually)t = 8 yearsPlugging in the values, we have:
\(FV = 480 * [(1 + 0.045/2)^(^2*^8^) - 1] / (0.045/2)\)
Calculating the expression inside the brackets
\((1 + 0.045/2)^(^2^*^8^) = 1.0225^1^6\)≈ 1.4197
Substituting this value back into the formula:
FV = 480 * (1.4197 - 1) / (0.045/2)
FV = 480 * 0.4197 / 0.0225
FV ≈ $8,876.80
So, the amount that can be withdrawn immediately after the last deposit is approximately $8,876.80.
Learn more about future value here :brainly.com/question/30741148
#SPJ1
pls answer this!!!
worth 30 points
find the circumference of a circle with d=97cm diameter
round to 3 significant figures
Answers
The circular is around 305 cm in circumeference.
The circumference of a circle is given by the formula:
C = πd
where d is the diameter of the circle.
Substituting d = 97 cm and using the value of π to be 3.14159, we get:
C = πd
C = 3.14159 × 97 cm
C ≈ 304.731 cm
Rounding this to 3 significant figures, we get:
C ≈ 305 cm
Therefore, the circumference of the circle is approximately 305 cm.
Learn more about circumference here:
https://brainly.com/question/6465134
#SPJ1
} One number is 8 times another. When the lesser number is subtracted from the greater, the result is 2 more than 5 times the lesser number. What are the numbers?
Answers
The numbers are 1 and 8.
We have,
Let's assume the lesser number as "x" and the greater number as "8x".
According to the given information, when the lesser number is subtracted from the greater, the result is 2 more than 5 times the lesser number:
8x - x = 5x + 2
Simplifying the expression:
7x = 5x + 2
Subtracting 5x from both sides:
2x = 2
Dividing both sides by 2:
x = 1
So, the lesser number is 1 and the greater number is 8 times that, which is 8.
Therefore,
The numbers are 1 and 8.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Consider the right rectangular prism.
What is the volume of the right rectangular prism, in cubic inches?

Answers
Answer:
430 and 1/2 cubic inches
Step-by-step explanation:
20.5 x 9 x 2.33 equals 429.885, which rounds up to 430 and 1/2 cubic inches
Determine the surface area and volume. Note: The base is a square.

Answers
Answer:
volume=60cm3, surface area=96cm2
Step-by-step explanation:
volume=1/3×(6×6)×5
=60cm3
surface area= 4(1/2×6×5)+(6×6)
=96cm2
3a-b=2
a+2b=3.
Elimination using Multiplication
Answers
Answer:
a=1
b=1
Step-by-step explanation:
Elimination using Multiplication
(3a-b=2) * 2 = 6a-2b=4
6a-2b=4 + a+2b=3 =
7a = 7
a = 7/7
a = 1
Substituting a =1 on a+2b=3
1+2b=3
2b = 3-1
b = 2/2
b = 1
I don’t know if that’s the correct answer and not sure if I did the table right helppp please :( !

Answers
To check if the given line is exponential, we can starting by making a table for a set of values. Let's do like in the picture, for x = 0, x = 1, x = 2:
\(\begin{gathered} (5\cdot0)^3=0^3=0 \\ (5\cdot1)^3=5^3=125 \\ (5\cdot2)^3=10^3=1000 \end{gathered}\)Here is the table then:
x | y
0 | 0
1 | 125
2 | 1000
For an exponential line, we can divide two y values of consecutive x values, and all consecutive values mus t be equal.
We would start by doing:
\(\frac{125}{0}\)And comparing it to
\(\frac{1000}{125}\)To see if they are equal. However, we can't divide by zero. Because of this, (5x)³ can't be exponential.
To be a linear line or straight line, the difference between consecutive values must be equal, so we should compare:
\(125-0=125\)With:
\(1000-125=875\)Because they are not equal, (5x)³ is not linear nor straight.
So it can't be alternatives A, B or C. So It has to be alternative D.
A worker is pouring milk for students lunches. She knows that 3 quarts of milk contain 12 cups. How many cups can she pour with 7 quarts of milk?
Answers
Answer:
7 quarts = 28 cups 10 cups = 2.5 quarts
Answer:
28 cups
Step-by-step explanation:
Fill in the blank with the correct answer choice. A ___________ has exactly one pair of parallel lines. a. square c. trapezoid b. parallelogram d. rectangle Please select the best answer from the choices provided A B C D
Answers
Answer: C
Step-by-step explanation:
The rest of the quadrilaterals provided have 2 pairs of parallel lines.
The choice is:
CExplanation:
The quadrilateral that has exactly one pair of parallel lines is called a trapezoid.
Here's what a trapezoid looks like :
\(\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\linethickness{0.3mm}\qbezier(0,0)(0,0)(1,3)\qbezier(5,0)(5,0)(4,3)\qbezier(1,3)(1,3)(4,3)\qbezier(3,0)(8.2,0)(0,0)\put(-0.5,-0.3){$\sf A$}\put(5.3,-0.3){$\sf B$}\put(4.2,3.1){$\sf C$}\put(0.6,3.1){$\sf D$}\end{picture}\)
Hence, this makes C the correct choice.PLEASE HELP ASAP I NEED THIS LIKE RIGHT NOW NO LINKS OR WILL BE REPORTED! SHOW ALL OF YOUR WORK! 3. The area of the square rug is 484 feet squared. (a) What is the length of one side? Write it as a square root. SHOW ALL OF YOUR WORK. (Hint: How do you find the area of a square? What is the equation?) (b) write the area as a number squared SHOW ALL OF YOUR WORK

Answers
Answer:
well,
it's more than (20ft)²
bc 20*20 =400
21² = 21 * 21 = 441
getting closer...
22² = 22 * 22 = 484
\( \sqrt{484} = {22}^{2} \)
yet, we arrived, short trip tough, pls leave the bus in an orderly manner
The Fahrenheit temperature readings on 66 Spring mornings in New York City are
summarized in the table below. Construct and label a frequency histogram of the data
with an appropriate scale.
Temp (°F) Number of Days.
30-39
2
40-49
26
50-59
28
60-69
8
70-79
2
Graph answer Click and drag to make a rectangle. Click a rectangle to delete it.
Answers
To construct a frequency histogram based on the given temperature data, we will use the temperature ranges as the x-axis and the number of days as the y-axis.
The temperature ranges and their corresponding frequencies are as follows:
30-39: 2 days
40-49: 26 days
50-59: 28 days
60-69: 8 days
70-79: 2 days
To create the histogram, we will represent each temperature range as a bar and the height of each bar will correspond to the frequency of days.
Using an appropriate scale, we can label the x-axis with the temperature ranges (30-39, 40-49, 50-59, 60-69, 70-79) and the y-axis with the frequency values.
Now, we can draw rectangles (bars) on the graph, with the base of each rectangle corresponding to the temperature range and the height representing the frequency of days. The height of each bar will be determined by the corresponding frequency value.
For such more question on frequency
https://brainly.com/question/254161
#SPJ8
Please answer this thank you

Answers
Answer:
The answer is B- X= 31/25
Answer:
x = 31/25
Step-by-step explanation:
Polygon ABCD is drawn with vertices A(−4, −4), B(−4, −6), C(−1, −6), D(−1, −4). Determine the image coordinates of B′ if the preimage is reflected across y = 3.
B′(−4, 6)
B′(−4, 12)
B′(−1, −3)
B′(10, −6)
Answers
To reflect a point across the line y=3, we find the point that is the same distance from y=3 as the original point, but on the opposite side of the line. In this case, the original point is B(−4,−6), which is 9 units below y=3. The image point will be 9 units above y=3, so it will have a y-coordinate of 3+9=12. The x-coordinate remains the same, so the image point is B
′
(−4,12).
5 Signs for science project displays are cut of poster board that measure 1 yard on each side. Each sign is-yard long and-yard wide. How ma signs can be cut from 1 piece of poster board? Wh the area of each sign? Show your work.
Answers
Answer:
\(\text{27}\)
Step-by-step explanation:
Given that :
\(\text{Dimension of poster board} = 1 \ \text{yd} \ \text{by} \ 1 \ \text{yd}\)
\(\text{Dimension of each poster board} = \dfrac{1}{3} \ \text{yd} \ \text{by} \ \dfrac{1}{9} \ \text{yd}\)
Number of poster signs that can be cut :
\(\text{Area of poster sign} = \dfrac{1}{3} \times \dfrac{1}{9} = \dfrac{1}{27} \ \text{yard}^2\)
\(\text{Area of poster board} = 1 \ \text{yard}^2\)
Number of poster signs that can be cut :
\(\dfrac{\text{Area of poster board}}{\text{Area of poster sign}}\)
\(1 \ \text{yard}^2\div (\dfrac{1}{27} ) \ \text{yard}^2\)
\(1 \div \dfrac{1}{27}\)
\(1 \times \dfrac{27}{1}\)
\(\bold{= 27 \ poster \ signs}\)
What is 4/5 ÷ 1/3? The quotient is 2 and
Answers
Answer:4/5 : 1/3=4/5 x 3/1=12/5
Step-by-step explanation:
Answer:
12/5
Step-by-step explanation:
If you set it in the calculator 4/5 ÷ 1/3 you get = 12/5
was it helpful?
18. The length of a hall is 15 metres. It is represented by a line 3 centimetres long on a scale drawing. What scale is used? (a) 1cm represents 1 metre (b) 1cm represents 2 metres (c) 1cm represents 3 metres (d) 1cm represents 5 metres (e) 1cm represents 15 metres
Answers
Simplify the problem first.
A 15 m line is represented as 3 cm long.
15 m = 3 cm
15/3 m = 3/3 cm
5 m = 1 cm
1 cm represents 5 metres. (d)
Hope this helps.
:)
- Jeron
Sandro would like to retire at age 60 with an income of $1500 per month from his
retirement savings. If he is to receive these payments until he is 90 years old, what
amount would he need in his retirement savings account at age 60, if the account
earns 4.5% compounded monthly?
Answers
The amount (present value at age 60) that Sandro would neet in his retirement savings account in order to have a monthly income of $1,500 until he is 90 years old, compounded at 4.5% monthly is $296,041.74.
How the present value is computed:The present value is computed using an online fiance calculator that discounts the future withdrawals (monthly income) for a 360-months period.
End of withdrawal period = 90 years old
Beginning of withdrawal period = 60 years old
The number of years between 60 and 90 = 30 years
N (# of periods) = 360 months (30 years x 12)
I/Y (Interest per year) = 4.5%
PMT (Periodic Payment) = $-1,500
FV (Future Value) = $0
Results:
Present Value (PV) = $296,041.74
Sum of all periodic payments = $540,000 ($1,500 x 360 months)
Total Interest = $243,958.26
Learn more about the present value at https://brainly.com/question/20813161.
#SPJ1
Erik Red is a player for the Arizona Snowflakes in the National Foosball League. The league has 25 teams, each with 73 players. Every week, 8 players per team are chosen for random drug testing.
A) What is the probability that Erik Red is chosen for random drug testing in a specified week of the foosball season?
B) What is the probability that Erik Red is chosen for random drug testing at least 5 times in the first 9 weeks of the foosball season?
C) What is the expected number of players who are chosen for random drug testing at least 4 times in the first 9 weeks of the foosball season?
D) Let Y be the number of players who are chosen for random drug testing at least 4 times in the first 9 weeks of the foosball season. What is the maximum possible value of Y, i.e., the largest k such that P(Y=k) > 0?
Answers
Answer:
8/73
0.10959
21 players
Step-by-step explanation:
Given that:
Number of teams = 25
Number of players per team = 73
Number of players chosen for drug testing = 8
A) What is the probability that Erik Red is chosen for random drug testing in a specified week of the foosball season?
Number chosen per team / number of players per team
8 / 73 = 0.10959
B) What is the probability that Erik Red is chosen for random drug testing at least 5 times in the first 9 weeks of the foosball season?
P( being chosen at least 5 times)
USing binomial. Distribution
P(X =x) = nCr * p^x * (1-p)^n-x
To save computation time, we can use the binomial distribution calculator :
P(x≥5):p(x = 5) + p(x = 6) + p(x =7) + p(x = 8) +. P(x = 9) = 0.00136
C) What is the expected number of players who are chosen for random drug testing at least 4 times in the first 9 weeks of the foosball season?
Number who are chosen atleast 4 times :
P(x ≥ 4) = p(x = 4) + p(x = 5) + p(x = 6) + p(x = 7) + p(x = 8) +. P(x =9) = 0.0115
P(x ≥ 4) * number of players per team * nunber of teams in league
0.0115 * 73 * 25 = 20.9875
= 21 players
D) Let Y be the number of players who are chosen for random drug testing at least 4 times in the first 9 weeks of the foosball season. What is the maximum possible value of Y, i.e., the largest k such that P(Y=k) > 0?
45 x 6 = 6 x 45 what multiplication property
Answers
Answer:
commutative property of multiplication
Step-by-step explanation:
doesnt matter 2*1 or 1*2 you will get the same answer
A 3-yard piece of cotton cloth costs $2.61. What is the price per foot?
Answers
The price per foot is $0.29
Given,
A 3-yard piece of cotton cloth costs = $2.61
1 Yard = 3 Foot
so, 3 Yard = 9 Foot
The Cost of cotton cloth per foot,
= 2.61/9
= 0.29
Therefore, the price per foot is $0.29
To learn more about Yard,
brainly.com/question/25829717
1,2,3,4,5 what is probability that an even number will be chosen?
Answers
Answer:
Step-by-step explanation:
step 1
100%/the total number = percent for one probability
100/5 = 20%
2 and 4 is even.
total even number * percent for one probability = total percent for even number
20% * 2 = 40%
therefore total even number is 40%
The probability is:
2/5Step-by-step explanation:
Remember the formula for probability:
\(\boxed{\!\!\boxed{\bold{Probability=\frac{Favourable~outcome}{total~outcomes}\quad}}\!\!}\)
In this case, the favourable outcome (an even number) is 2, because there are only 2 even numbers in the set.
As for the total outcomes, there are 5 of them, because we have 5 numbers total.
So the probability of choosing an even number is 2/5.