Answers
Answer:
area = 164
Step-by-step explanation:
Divide the square into 2 pictures.
; Square 1 = 5×2 = 10
Square 2 = 14×11 (11 from 16-5 )
so, square 2 = 154
all of area = 154+10 = 164
hope it helps ☺️
Related Questions
I need helppp quickkkk

Answers
The triangles QRS and TUV are similar. They are similar as ΔTUV = 3ΔQRS.
What are triangles?
Triangles are a particular sort of polygon in geometry that have three sides and three vertices. Three straight sides make up the two-dimensional figure shown here. An example of a 3-sided polygon is a triangle. The total of a triangle's three angles equals 180 degrees. One plane completely encloses the triangle.
There are two similar looking triangles, ΔQRS and ΔTUV.
In ΔQRS, the measure of line segment QR = 9 units
In ΔQRS, the measure of line segment RS = 10 units
In ΔQRS, the measure of line segment QS = 11 units
In ΔTUV, the measure of line segment TU = 27 units
In ΔTUV, the measure of line segment UV = 30 units
In ΔTUV, the measure of line segment TV = 33 units
The pattern here can be seen that -
For the line segment TU -
3 (QR) = TU
3 (9) = 27
Similarly, for the line segment UV -
3 (RS) = UV
3 (10) = 30
Similarly, for the line segment TV -
3 (QS) = TV
3 (11) = 33
Therefore, the triangle TUV is three times scaled version of triangle QRS.
To learn more about triangles from the given link
https://brainly.com/question/25215131
#SPJ1
Write the equation in standard form for the hyperbola with vertices (-2,0) and (2,0) and a conjugate axis of length 14
Answers
Solution
- The equation of a hyperbola is given s:
\(\begin{gathered} \frac{(x-h)^2}{a}-\frac{(y-k)^2}{b}=1 \\ \\ where, \\ coordinates\text{ of the vertices}=(h\pm a,k) \\ Length\text{ of conjugate axis}=2b \end{gathered}\)- Thus, we can find that:
\(\begin{gathered} (\pm2,0)=(h\pm a,k) \\ \\ k=0 \\ \therefore h+a=2 \\ h-a=-2 \\ \text{ Subtract both equations, we have:} \\ 2a=4 \\ a=\frac{4}{2}=2 \\ \\ h+a=2 \\ h+2=2 \\ h=2-2=0 \\ \\ \text{ Thus, we have that the center of the hyperbola is: }(h,k)=(0,0) \\ \\ 2b=14 \\ \text{ Divide both sides by 2} \\ b=\frac{14}{2}=7 \end{gathered}\)Final Answer
The equation of the parabola is:
\(\frac{x^2}{2^2}-\frac{y^2}{7^2}=1\)If a coin is tossed twice, what is the probability of getting a head or a tail? Is it one or 1/2?
Answers
1/4
The sample space of two tossed coins is:S: {(H,H),(H,T),(T,H),(T,T)}Probability= (No. of favourable outcomes)/Total. no of outcomes)Here, from the sample space,P (getting 2 heads when a coin is tossed twice) = 1/4brainlyeveryday
50x=10 please help!!!
Answers
Answer:
\(\boxed{\boxed{\tt x=\frac{1}{5}}\: \bf Or\:\boxed{\tt x=0.2}}\)
Step-by-step explanation:
\(\tt 50x=10\)
Divide both sides by 50:-
\(\tt \cfrac{50x}{50}=\cfrac{10}{50}\)
Simplify:-
\(\tt x=\cfrac{1}{5}\)
_____________________
Hope this helps!
Have a great day!
Can you please help?

Answers
Answer:
Your answer is D
Step-by-step explanation:
45 divided by 5 equals 9
Answer:
easy 45 dived by 9 is 5
Step-by-step explanation:
hope it helps
Mike an experienced bricklayer can build a wall in 5 hours while his son, who is learning can do the job in 20 hours. How long does it take for them to build a wall together.
Answers
Answer:
4 hours
Explanation:
Mike can build a wall in 5 hours. His work rate is:
\(\frac{1}{5}\)His son can do the job in 20 hours. The son's work rate is:
\(\frac{1}{20}\)Let the time it takes both of them = x hours. Then, their joint rate is:
\(\frac{1}{x}\)Therefore:
\(\frac{1}{5}+\frac{1}{20}=\frac{1}{x}\)We solve the equation for x:
\(\begin{gathered} \frac{4+1}{20}=\frac{1}{x} \\ \frac{5}{20}=\frac{1}{x} \\ \text{ Cross multiply} \\ 5x=20 \\ \text{ Divide both sides by 5} \\ \frac{5x}{5}=\frac{20}{5} \\ x=4\text{ hours} \end{gathered}\)It takes them 4 hours to build a wall together.
what is 2/3 divide by 2/9
Answers
Answer:
3
Step-by-step explanation:
(2/3)/(2/9) = (2/3) * (9/2) = 3
6) Girls at CRHS have an average height of 65.5 inches with standard deviation of 2.3 inches. Boys have an
average height of 71 inches with standard deviation of 3.5 inches. If girls and boys were picked
at random and the difference in height calculated, what would the average height difference
be? What would the standard deviation of the differences in height be?
WILL MARK AS BRAINLIEST
Answers
Answer:
The average height difference between randomly selected girls and boys is 5.5 inches. The standard deviation of the difference in height is about 4.18808 inches.
Step-by-step explanation:
Just subtract the girls' average from the boys' average to find the average difference between any girl and boy.
Calculate the variance from the given standard deviations (square the SD). Add the variances and find the square root of that sum. (SD = square root of Var).
The standard deviation is only able to be calculated when the two variables are independent.
The variances are added and not subtracted because finding a different average doesn't mean that the data that is being observed also has a different deviation (also there isn't really a situation where you would subtract the Var).
what’s the value of x?

Answers
Answer:
x=7
Step-by-step explanation:
what value of y will make the equation true?

Answers
You conduct a statistical test of hypotheses and find that the null hypothesis is statistically significant at level α = 0.05. You may conclude thatA. the test would also be significant at level α = 0.10.B. the test would also be significant at level α = 0.01.C. both options one and two are true.D. neither options one or two is true.
Answers
If the null hypothesis is statistically significant at level α = 0.05, it means that the probability of obtaining the observed result by chance is less than 5%. Therefore, the correct answer is A. Therefore, if we increase the significance level to α = 0.10, which means allowing for a higher probability of obtaining the observed result by chance, the test would still be significant.
When conducting a statistical hypothesis test, a significance level is set to determine whether to reject the null hypothesis or not. A common significance level is α = 0.05, which means that if the probability of obtaining the observed result by chance is less than 5%, we reject the null hypothesis. If the null hypothesis is statistically significant at α = 0.05, it means that the observed result is unlikely to have occurred by chance, and we have evidence to support the alternative hypothesis.
If we increase the significance level to α = 0.10, we are allowing for a higher probability of obtaining the observed result by chance. Therefore, the test would still be significant if it was statistically significant at α = 0.05, but may not be significant at α = 0.01, which requires a lower probability of obtaining the observed result by chance. It's important to note that the standard normal distribution is not uniform, but rather bell-shaped, symmetric about the mean, and unimodal. Therefore, option B, which states that the standard normal distribution is uniform, is not true, while options C and D are also not true.
Learn more about statistical hypothesis test:
https://brainly.com/question/29576929
#SPJ11
Which of the following is equal to square root 9•16
O A. 36
B. Square root 9•square root 16
C. 144
D.Square root 9/16

Answers
Answer:
Letter B
9.16
...........
.
Find the selling price for each item given the cost and
the percent of markup or discount.
36. tennis shoes: $85; 24% discount

Answers
Answer:
$64.60
Step-by-step explanation: I believe this is right if not sorry. The first step is to multiply $85 by .24 and that is $20.40. Then take $20.40 from $85 (85-20.40) which is $64.60
Show that x(x - 1)(x + 1) = x³ - x
Answers
x (x - 1) (x + 1) = \(x^{3}\)- x
Distribute
1. (x + 1) \(x^{2}\) - x (x + 1) = \(x^{3}\) - x
2. Distribute
(x + 1) \(x^{2}\) - x (x + 1) = \(x^{3}\) - x
\(x^{3 }\) + 1 \(x^{2}\) - x (x + 1) = \(x^{3 }\) - x
3. Multiply by 1
\(x^{3 }\) + 1 \(x^{2}\) - x (x + 1) = \(x^{3 }\) - x
\(x^{3 }\) + \(x^{2}\) - x (x + 1) = \(x^{3 }\) - x
4. Distribute
\(x^{3 }\) + \(x^{2}\) - x (x + 1) = \(x^{3 }\) - x
\(x^{3 }\) + \(x^{2}\) - (\(x^{2}\) + x) = \(x^{3 }\) - x
5. Distribute
\(x^{3 }\) + \(x^{2}\) - (\(x^{2}\) + x) = \(x^{3 }\) - x
\(x^{3 }\) + \(x^{2}\) - \(x^{2}\) - x = \(x^{3 }\) - x
6. Combine like terms
\(x^{3 }\) + \(x^{2}\) - \(x^{2}\) - x = \(x^{3 }\)- x
\(x^{3 }\) - x = \(x^{3 }\) - x
7. Move terms to the left side
\(x^{3 }\) - x = \(x^{3 }\) - x
\(x^{3 }\) - x - (\(x^{3 }\) - x) = 0
8. Distribute
\(x^{3 }\) - x - (\(x^{3 }\) - x) = 0
\(x^{3 }\) - x - \(x^{3 }\) + x = 0
9. Combine like terms
\(x^{3 }\) - x - \(x^{3 }\) + x = 0
- x + x = 0
10. Combine like terms
- x + x = 0
0 = 0
To know more about like terms
https://brainly.com/question/3750096
what is the y and x intercept of 15x + 20y =1800?
Answers
Which means that the x intercept is 120 and the y intercept is 90.
20y = 1800
Divide by 20 on both sides
y = 90
15x = 1800
Divide 15 on both sides
x = 120
After the bank cashed a check Maureen wrote for $60, her balance was Negative 14 dollars. The equation b + (negative 60) = negative 14 can be used to represent this situation, where b is Maureen’s balance, in dollars, before the check was cashed. Maureen attempted to solve the equation using the steps below. b + (negative 60) = negative 14. Subtract 60 from both sides. B = negative 74. What error, if any, did Maureen make? Maureen’s work is correct, and her original balance was -$74. Maureen should have added 60 to both sides. Maureen should have added 14 to both sides. Maureen made a computational error when she subtracted 14 minus 60.
Answers
Answer:
-74
Step-by-step explanation:
Answer: -74
Step-by-step explanation:
Pls help only answer 1-73 an 1-74 pls I give brainlest

Answers
Answer:
Step-by-step explanation:
1-73
18 inches = 1.5 feet
Multiply 2 on both sides;
36 inches = 3 feet
As for 72 inches, multiply each side by 4
18 inches = 1.5 feet
72 inches = 6 feet
As for 144 inches, divide both sides by 18
1 inch is approximately 0.083
Multiply both sides by 144
144 inches = 12 feet
1-74
a. The scale goes by 20. 0->20->40, etc.
b. The scale goes by 15. 0->15->30, etc.
c. The scale goes by 25. 0->25->50, etc.
d. The scale goes by 50. 0->50->100, etc.
The cost of 6 pounds
of coffee is $3.
Answers
Answer:
ok 2 pound per 1 doller and 1 pund per0.50 cent
Step-by-step explanation:
Divide using long division . -4x^2+12x^3-7x+2 by 2x^2 +1
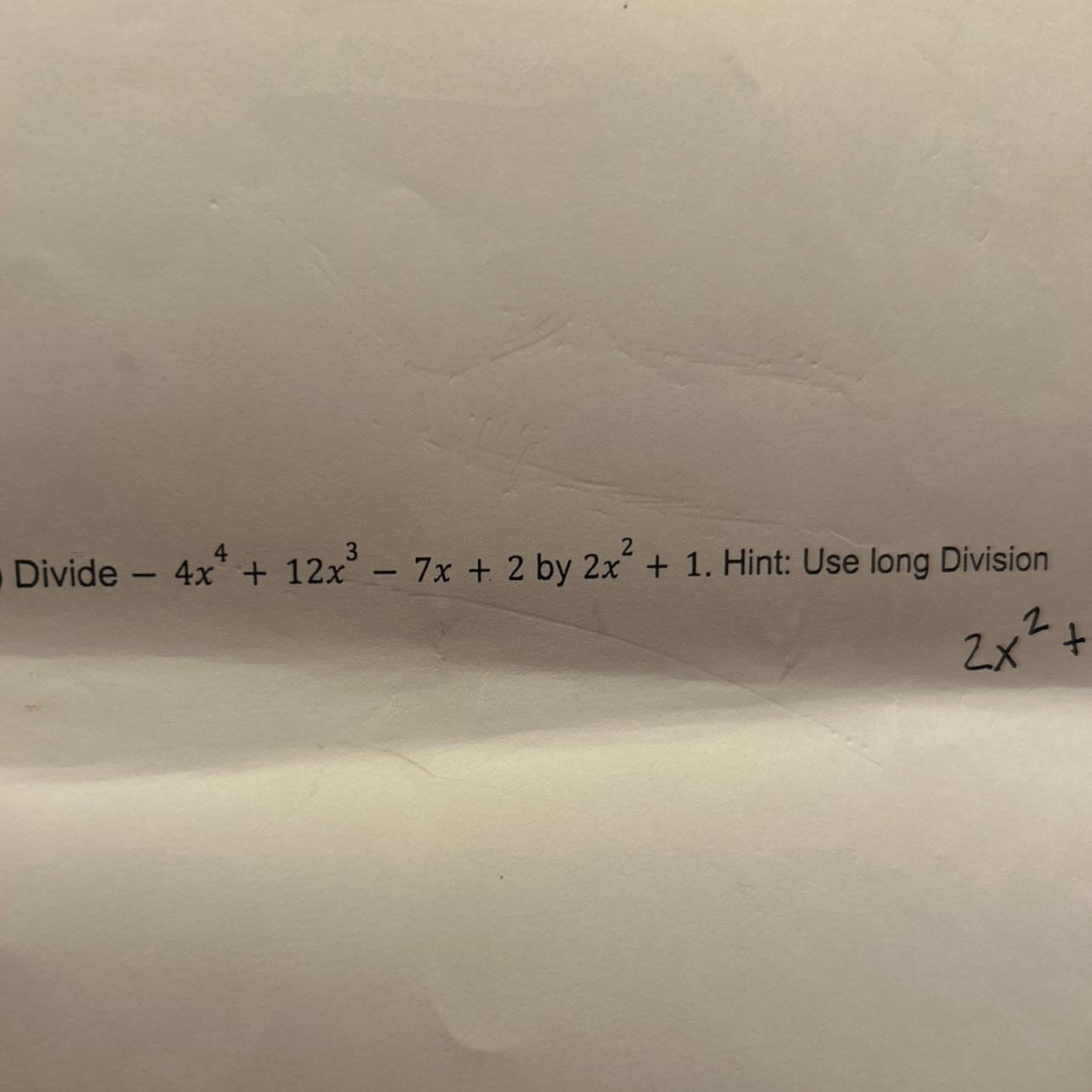
Answers
The quotient is -2x2 + 8x3 - 7x + 2 and indeed the remainder is 0, according to the question.
What is an example of long division?We can put the division symbol "" between two integers to indicate that they have been split. As an illustration, we may write 36 6 to represent the division of 36 by 6. Additionally, we may represent it as the fraction 366.
To divide\(-4x^2 + 12x^3 - 7x + 2\) by \(2x^2 + 1\)using long division, we write out the division in the form:
\(2x^2 + 1\)
\(-4x^2 + 12x^3 - 7x + 2\)
Step 1: Divide the first term of the dividend (\(-4x^2\)) by the first term of the divisor (2x^2). We get -2x^2.
Step 2: Multiply the entire divisor (\(2x^2 + 1\)) by \(-2x^2.\) This gives us\(-4x^4 + -2x^2.\)
Step 3: Subtract this result from the dividend, updating the dividend to \(8x^3 - 7x + 2.\)
Step 4: Repeat the process until the degree of the remainder is less than the degree of the divisor. In this case, the final remainder is non-zero, so we have:
\(2x^2 + 1\)
\(-4x^2 + 12x^3 - 7x + 2\)
\(-2x^2\)
\(8x^3 - 7x + 2\)
\(8x^3 - 7x + 2\)
So the quotient is \(-2x^2 + 8x^3 - 7x + 2\) and the remainder is 0.
To know more about Long division visit :
https://brainly.com/question/28824872
#SPJ1
13.10 − Let Mn be the maximum of n independent U(0,1) random variables. a. Derive the exact expression for P(∣Mn−1∣>ε). Hint: see Section 8.4. b. Show that limn→[infinity]P(∣Mn−1∣>ε)=0. Can this be derived from Chebyshev's inequality or the law of large numbers?
Answers
This can be derived using Chebyshev's inequality, as Chebyshev's inequality and the law of large numbers are different in nature.
Let M_n be the maximum of n independent U(0, 1) random variables.
To derive the exact expression for P(|M_n − 1| > ε), we need to follow the below steps:
First, we determine P(M_n ≤ 1-ε). The probability that all of the n variables are less than 1-ε is (1-ε)^n
So, P(M_n ≤ 1-ε) = (1-ε)^n
Similarly, we determine P(M_n ≥ 1+ε), which is equal to the probability that all the n variables are greater than 1+\epsilon
Hence, P(M_n ≥ 1+ε) = (1-ε)^n
Now we can write P(|M_n-1|>ε)=1-P(M_n≤1-ε)-P(M_n≥1+ε)
P(|M_n-1|>ε) = 1 - (1-ε)^n - (1+ε)^n.
Thus we have derived the exact expression for P(|M_n − 1| > ε) as P(|M_n-1|>ε) = 1 - (1-ε)^n - (1+ε)^n
Now, to show that $lim_{n\to\∞}$ P(|M_n - 1| > ε) = 0 , we can use Chebyshev's inequality which states that P(|X-\mu|>ε)≤{Var(X)/ε^2}
Chebyshev's inequality and the law of large numbers are different in nature as Chebyshev's inequality gives the upper bound for the probability of deviation of a random variable from its expected value. On the other hand, the law of large numbers provides information about how the sample mean approaches the population mean as the sample size increases.
Learn more about Chebyshev's inequality:
https://brainly.com/question/32750368
#SPJ11
What is the result of 3 divided by three-fifths?

Answers
\(\dfrac{3}{\tfrac 35} = 3 \times \dfrac 53 = 5\)
Answer:
5
Step-by-step explanation:
3 -> \(\frac{3}{1}\)
Method is "Keep, Change, Flip"
\(\frac{3}{1} / \frac{3}{5} =\frac{3}{1} * \frac{5}{3} = \frac{15}{3} = 5\)
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly. (ノ^∇^)
- Heather
f(x) = 8 – 3x
Evaluate f(9)
Answers
f(9) = 8 - 3(9)
= 8 - 27
= -19
hope this helps!
Find the value of y in the diagram.

Answers
Answer:
6.3
Step-by-step explanation:
y/9=7/10
cross multiply
10y=63
y =6.3
PLS help what is f(0)?????

Answers
Answer: -4
Step-by-step explanation:
When a question says f(0), this means that the function is being evaluated at the point x = 0. For this problem in specific, the function f(x) is defined as a piecewise function, which means you will have to use the 3 different pieces depending on the value of 'x' you are dealing with.
For this problem, x = 0. This means that the third piecewise function must be used. I hope you can understand what I'm trying to explain. You use the different piecewise functions depending on the 'x' value.
Okay so let's use the third piecewise function:
\(f(x)=-x-4\)
\(f(0)=-0-4\)
\(f(0)=0-4\)
\(f(0)=-4\)
PLEASE HELP
What two numbers that add each other give you -7 but times it give you -120
Answers
To solve this I set up a system of equations. When you add two numbers, let’s say x and y, together you get -7. My first equation is x+y=-7. My second equation is xy=-120, because when you multiply them together you get -120.
x + y =-7
xy = -120
I solved by substitution, so I first got one variable (in this case y) alone on one side of the equation. Let me know if you want me to explain any of these steps further.
x+y = -7
y = -7 - x
I then substituted -7 - x in for y in the other equation.
xy = -120
x(-7 - x) = -120
From here I distributed the x.
-7x -x^2 = -120
-x^2 -7x +120 = 0
-1(x^2 + 7x -120) = 0
-(x-8)(x+15) = 0
x=8,-15
I factored the polynomial to solve for x.
8 + y = -7
y = -15
-15 + y = -7
y = 8
Finally, I solved for y using these values for x. Either way the numbers you get are -15 and 8. To double check this, see that -15+8=-7 and -15(8) =-120
I hope this helps!
The distance traveled (in meters) by an insect is modeled by the equation d=0.3t where d is the distance traveled in meters and t is the time in minutes. Find the distance traveled in 26.3 minutes. A. 0.789 meters B. 87.67 meters C. 26 meters D. 7.89 meters
Answers
Answer:
D. 7.89 meters
Step-by-step explanation:
Given,
d = 0.3t
Here,
t = 26.3
Therefore,
d = 0.3*26.3
= 7.89m
If the balance at the end of eight years on an investment of $700 that has been invested at a rate of 5% is $980 how much was the interest
Answers
Answer:
To calculate the interest earned on an investment, we need to subtract the initial investment from the final balance.
The initial investment is $700, and the final balance after 8 years of investment at a rate of 5% is $980.
The interest earned can be calculated as:
Final balance - Initial investment = Interest earned
$980 - $700 = $280
Therefore, the interest earned on the investment of $700 at a rate of 5% for 8 years is $280.
In the following number, 3 x 106 indicate
the coefficient_______________and exponent________
Answers
In the number 3 × 106, 3 is the coefficient and 106 is the exponent. A coefficient is the numerical factor of a term that includes a variable raised to a power in an algebraic expression,
whereas an exponent is the number of times a quantity is multiplied by itself in an exponentiation expression.According to the laws of exponents,
multiplying the same base number is equivalent to adding their exponents. In this example, 106 represents that the base number (10) is multiplied by itself six times, giving us 1,000,000 (10 × 10 × 10 × 10 × 10 × 10).Therefore, 3 × 106 is equal to 3,000,000.
To know more about coefficient visit:
https://brainly.com/question/1594145
#SPJ11
an automotive manufacturer wants to know the proportion of new car buyers who prefer foreign cars over domestic. in an earlier study, the population proportion was estimated to be 0.31 . how large a sample would be required in order to estimate the fraction of new car buyers who prefer foreign cars at the 95% confidence level with an error of at most 0.03 ? round your answer up to the next integer.
Answers
The required sample size is 907.
We have,
To determine the required sample size for estimating the fraction of new car buyers who prefer foreign cars over domestic with a 95% confidence level and an error of at most 0.03, we'll use the following formula:
n = (Z² x p (1 - p)) / E²
Where:
- n is the required sample size
- Z is the Z-score for the desired confidence level (1.96 for a 95% confidence level)
- p is the estimated population proportion (0.31)
- E is the margin of error (0.03)
Step-by-step calculation:
1. Calculate Z²: 1.96² = 3.8416
2. Calculate p (1 - p): 0.31 x (1 - 0.31) = 0.2139
3. Calculate E²: 0.03² = 0.0009
4. Substitute these values into the formula: n = (3.8416 x 0.2139) / 0.0009 = 906.92
Since we need to round up to the next integer, the required sample size is 907.
Thus,
The required sample size is 907.
Learn more about confidence interval here:
https://brainly.com/question/14979512
#SPJ11
Which graph shows the solution set for 2x+3>-9?
Look at the picture

Answers
Answer:
it's the last one
Step-by-step explanation:
2x+3>-9
2x>-12
x>-6
Answer:
D
2x+3>-9
Move the constant the the right
2x>-9-3
Calculate
2x> -12
Divide both side
x> -6
(-6,+ 00)