find the sum of the first 10 terms of the following series, to the nearest integer. 2,8,32,128,... ?
Answers
Hence, option B is the correct answer. The given expressions are:Expression A: `-5(x - 1)`Expression B: `(5 - 5)x`Expression C: `-5x`Expression D: `5x`Expression E: `5 - 5x`
We are to find the expression that is not equivalent to the others. Expression A can be simplified using the distributive property of multiplication over addition: `-5(x - 1) = -5x + 5`Expression B can be simplified using the distributive property of multiplication over subtraction: `(5 - 5)x = 0x = 0`Expression C is already in simplest form. Expression D is already in simplest form.
Expression E can be simplified using the distributive property of multiplication over subtraction: `5 - 5x = 5(1 - x)`Therefore, the expression that is not equivalent to the others is option B, `(5 - 5)x`, because it is equal to 0 which is different from the other expressions. Hence, option B is the correct answer.
To know more about multiply visit:
https://brainly.com/question/23536361
#SPJ11
Related Questions
HELP PLEASEEEEE AND THANK YOUU !!!!!!!!!

Answers
4. Assume that the sales of a certain appliance dealer are approximated by a linear function. Suppose that sales were $850,000 in 1992 and $1,262,500 in 1997. X = 0 represents 1992. (a) Find an equation giving the dealer's yearly sales. (b) What were the dealer's approximate sales in 1995? (c) Estimate sales in 1999.
Answers
The answer are:
a. S(x) = $82,500(x - 1992) + $850,000
b. Sales in 1995: $1,097,500
c. Sales in 1999: $1,427,500
To solve this, we need to crea a linear function. A linear function is of the form:
\(L(x)=ax+b\)Where a is the slope and b the y-intercept.
We want the sales in function of the year. If we call the year x, and teh sale S, we call the line S(x)
The first thing we need to do is to find the slope of the line. We can calculate the slope of the line with two points like:
\(\begin{gathered} P=(x_p,y_p)\text{ and Q}=(x_q,y_q) \\ \text{slope}=\frac{y_q-y_p}{x_q-x_p} \end{gathered}\)
For two points P and Q. We know the value of two points:
In 1992, the sales was $850,000
In 1997, the sales was $1,262,500
Then we call P = (1992, $850,000) and Q = (1997, $1,262,500)
Now let's calculate the slope:
\(slope=\frac{1,262,500-850,000}{1997-1992}=\frac{412,500}{5}=82,500\)Now that we know the slope, we need to find the term b of the form of a line.
b is the value of the function when x = 0. In this case, the problem says that when x = 0, we need to use the value of 1992. The sales in 1992 was $850,000. then b = $850,000
We almost done with a. the only thing remaining is that we want the year 1992 to be the starting point. Then, to our value of x, we need to rest 1992.
let's see:
\(\begin{gathered} \text{slope}=82,500 \\ b=850,000 \\ S(x)=82,500\cdot x+850,000 \end{gathered}\)If we just left the equation like that, when we want to know what happens in 1992:
\(S(1992)=82,500\cdot1992+850,000=165,190,000\)Which we know is wrong because the sales in 1992 were 850,000. To fix this, we need to rest 1992 from x. This way:
\(S(x)=82,500(x-1992)+850,000\)If we try this equation for 1992:
\(\begin{gathered} S(1992)=82,500(1992-1992)+850,00 \\ S(1992)=82,500\cdot0+850,000 \\ S(1992)=850,000 \end{gathered}\)And that's the correct value of the sales for 1992.
This was the hard part, all we have to do now is evaluate the function for x = 1995 and x = 1999:
Part b.
\(\begin{gathered} S(x)=82,500(x-1992)+850,000 \\ S(1995)=82,500(1995-1992)+850,000 \\ S(1995)=82,500\cdot3+850,000 \\ S(1995)=1,097,500 \end{gathered}\)Part c.
\(\begin{gathered} S(1999)=82,500(1999-1992)+850,000 \\ S(1999)=82,500\cdot7+850,000 \\ S(1999)=1,427,500 \end{gathered}\)And the problem is solved
community gym charges a 60$ membership fee and a 70$ monthly fee. workout gym charges a 190$ membership fee and a 60$ monthly fee
Answers
For 13 months the membership is done using the equivalent of two given monthly fees for community and workout gym.
Why do you use the word equivalent?Algebraic equations with equivalent solutions or roots are called equivalent equations. An analogous equation is one that is created by adding or removing the identical quantity or expression from both sides of a given equation. An equation is equivalent if both sides are multiplied or divided by the same non-zero value. By dividing both numbers by the same number, one can convert a division problem into an analogous problem while keeping the ratio between the two numbers constant. The equivalent is defined as something that is almost identical to or equal to another object. Two numbers that are equivalent are (2+2) and 4. These two things are equivalent since 2+2=4. equal to make equivalent.
Let x be the months
then community month= workout month
60+70x=190+60x
⇒70x-60x=190-60
⇒10x=130
⇒x=13 be the months be the working.
To know more about equivalent equations, click here:
https://brainly.com/question/17357101
#SPJ4
find the axis of symmetry for this parabola y=-2x^2-4x-11
write your answer as an equation
Answers
Answer:
x = - 1
Step-by-step explanation:
Given a parabola in standard form
y = ax² + bx + c ( a ≠ 0 ) , then the equation of the axis of symmetry is
x = - \(\frac{b}{2a}\)
y = - 2x² - 4x - 11 ← is in standard form
with a = - 2 and b = - 4 , thus
x = - \(\frac{-4}{-4}\) = - 1
x = - 1 is the equation of the axis of symmetry
Suppose a floating point number: 010000001100000000… What is its decimal value? (don't enter fractions; enter decimal values. E.g., for 1/4 type .25) Question 7 Suppose a floating point number: 010000010110100000… What is its decimal value? (don't enter fractions; encer clecimal walues. E.g., for 1 and 1/4 type 1.25) Question 8 Convert the following float to decimal: 110000001111110…….…
Answers
The decimal value of the floating-point number 110000001111110... is approximately -0.000000015935.
A 32-bit binary number is the floating-point number 010000010110100000... We must interpret its components in accordance with the IEEE 754 standard for single-precision floating-point representation before we can convert it to decimal.
The number's sign is represented by the first bit, which is 0. The number is positive because it is zero.
The exponent is represented by the next eight bits, 10000010 The bias value, which is 127 for single-precision, needs to be subtracted in order to determine the exponent's decimal value. As a result, the value of the exponent is -25: 10000010 - 127.
The binary fractional part is represented by the remaining 23 bits, which are 110100000... Summing the series of 2(-i) for each bit I that is set to 1, we convert the fractional part to a decimal fraction for the purpose of determining its decimal value. The series is as follows, starting with the leftmost bit:
The decimal value of the floating-point number is then calculated as follows: 1/2 + 1/8 + 1/16 + 1/32 = 0.53125.
The floating-point number 010000010110100000... has a decimal value of approximately 0.0000000938776, which is equal to (-1)0 * 1.53125 * 2(-25).
8th Question: The 32-bit binary number 110000001111110... is a floating-point number. Using the same procedure as before:
The number's sign is represented by the first bit, which is 1. The number is negative because it is 1.
The exponent is represented by the next eight bits, 10000011 We get the exponent value of 10000011 - 127 = -24 when we subtract the bias value of 127.
In binary, the fractional part of the number is represented by the remaining 23 bits, which are 111110... Switching it over completely to a decimal division gives us the series:
1/2 plus 1/4 plus 1/8 plus 1/16 plus 1/32 equals 0.96875, so the floating-point number's decimal value is as follows:
The floating-point number 110000001111110... has a decimal value of (-1)1 x 1.96875 x 2 (-24), which is approximately -0.000000015935003662109375.
To know more about Decimal, visit
brainly.com/question/28393353
#SPJ11
The design plans for a new concert hall show elevations relative to ground level
at 0 feet. The elevation of the balcony floor is 37 feet, and the elevation of the
basement floor is -17 feet.
Fill in the blanks to write the distances of the balcony and basement from ground level.
Answers
Answer:
54 FT
Step-by-step explanation:
|37| = 37
|-17| = 17
37 + 17 = 54 feet between the balcony and the basement
Please give brainliest :D
If z^3= x^3 + y^2, dx/dt=3, dy/dt=2, and z>0, find dz/dt at (x,y) =(4,0). Please give an exact answer. Provide your answer below:
Answers
The rate of change of z with respect to t, dz/dt, at (x,y) = (4,0) is equal to 48, based on the given equations and the differentiation of z³ = x³ + y².
To find dz/dt at (x,y) = (4,0), we need to differentiate the equation z³ = x³ + y² with respect to t.
Differentiating both sides of the equation, we get:
3z² * dz/dt = 3x² * dx/dt + 2y * dy/dt
Given dx/dt = 3 and dy/dt = 2, and since (x,y) = (4,0), we have
3z² * dz/dt = 3(4)² * 3 + 2(0) * 2
3z² * dz/dt = 3(16) * 3
3z² * dz/dt = 144z²
Now, let's solve for dz/dt
dz/dt = (144z²) / (3z²)
dz/dt = 48
Therefore, dz/dt at (x,y) = (4,0) is equal to 48.
To know more about differentiate:
https://brainly.com/question/24062595
#SPJ4
Evaluate the integral. ∫ x sec x tan x dx
Answers
The integral is ∫ x sec x tan x dx. We can solve it using integration by parts xln|sec(x) + tan(x)| - x + C
We have u = x, dv = sec(x)tan(x)dx, du = dx, and v = ln|sec(x) + tan(x)|.
The integral is then
Integrating the second part we get:
xln|sec(x) + tan(x)| - x + C
The integral is ∫ x sec x tan x dx. We can solve it using integration by parts. We let u = x and dv = sec(x)tan(x)dx. Then, du = dx and v = ln|sec(x) + tan(x)|. So, the integral becomes xln|sec(x) + tan(x)| - ∫ ln|sec(x) + tan(x)| dx. We can integrate the second part to get xln|sec(x) + tan(x)| - x + C.
Learn more about integral here
https://brainly.com/question/18125359
#SPJ4
Answer this question!!!!!!!!!! plsss

Answers
the price is already discounted, so then you just multiply 546.7*.10 and that equals 54.67
subtract 54.67 from 546.7
the total is now 492.03
Answer: $492.03
Step-by-Step explanation: just multiply 546.7*.10 and that equals 54.67
subtract 54.67 from 546.7
the total is now 492.03
How many hours must you drive if you drive 643 miles at 65 mph on the interstate? Round to the nearest tenth hour
Answers
Answer:
9.9 hours, rounded to the nearest tenth hour.
Step-by-step explanation:
To calculate the time of travel, we must first divide the distance by the speed. Why, you ask? Because of this equation:
\(Speed\=\ \frac{distance}{time}\)
Therefore, with a little bit of arrangement, we get:
\(Time\=\ \frac{distance}{speed}\)
So, let's get on with it.
\(Time\=\ \frac{643 \ miles}{65 \ mph}\)
\(Time\=\ 9.9 \ hours \)
Finally, we have our answer: 9.9 hours, rounded to the nearest tenth.
Hope this helped!
Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement.If f(x)=2x−x2+1/3x3.⋯………. converges for all x, then f′′′(0)=2.
Answers
The statement given is false. The reason for this is that the convergence of a function does not necessarily imply anything about the value of its derivative. To disprove the statement, we can consider the function f(x) = x^2, which converges for all x, but its third derivative f'''(x) = 0, which means that f'''(0) is also equal to 0. Hence, f′′′(0) is not equal to 2.
In general, it is important to note that the convergence of a function does not provide any information about the behavior of its derivatives. Moreover, a function may converge at some points and diverge at others, and this can be determined by analyzing the behavior of its terms or by using convergence tests. In this case, it is necessary to compute f′′′(0) directly using the definition of the derivative or by applying differentiation rules.
To know more about statement visit:
https://brainly.com/question/32267897
#SPJ11
75 basketballs cost $1,143.75. Find the unit rate in price per basketball.
Answers
Answer:
$15.25 per basketball
Step-by-step explanation:
1,143.75/75=15.25
HELP A MF OUT!!!! NO LINKS THOO
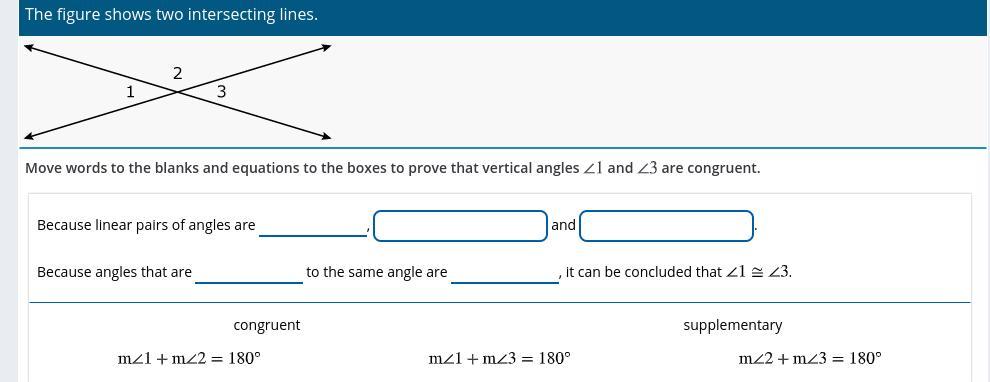
Answers
Answer:
1-m< +m<2 =180°
2-congruent
3-supplementary
4-m<1 + m<3 = 180°
5-m<2 + m<3 = 180°
Sarah's surfboards charges a fee of $60 to rent a surfboard and then $10.50 per hour. Sally's surfboards does not charge a fee, but they cost $15.50 per hour. At how many hours will the cost be the same to rent a surfboard for each shop?
Answers
Answer:
12 hours
Step-by-step explanation:
Let the number of hours be represented as h.
Sarah's surfboards charges a fee of $60 to rent a surfboard and then $10.50 per hour.
Mathematically ,
60 + 10.50h
Sally's surfboards does not charge a fee, but they cost $15.50 per hour
Mathematically,
15.50h
Equating both equations together
60 + 10.50h = 15.50 h
Collect like terms
60 = 15.50h - 10.50h
60 = 5h
h = 60/5
h = 12 hours
Therefore, the number of hours that the cost will be the same to rent a surfboard for each shop is 12 hours.
what is 45,037.36 in word form
Answers
The question requires you to write in word for the number 45,037.36
The number has a decimal
This will be written as;
Fourty five thousand and thirty seven and thirty-six hundredths.
find the limit if it exists. if it does not exist, explain why. lim (x;y)→(0;0) y^2 sin^2 (x) x^4 + y4
Answers
rearrange this equation to isolate c. a=b(1c−1d)
Answers
The equation, rearranged to isolate c, is: c = (a + bd) / b
In order to isolate c, we need to get c by itself on one side of the equation. Here's how we can do that:
First, we can distribute the b to get:
a = bc - bd
Next, we can add bd to both sides of the equation:
a + bd = bc
Finally, we can divide both sides by b to isolate c:
(a + bd) / b = c
The equation, rearranged to isolate c, is: c = (a + bd) / b
Know more about equations here:
https://brainly.com/question/29174899
#SPJ11
Find the vertex of the parabola.
y = 2x^2+ 8x+12
a.
(2,-4)
b. (-2,4)
c. (-4,2)
d.
(4,-2)
Answers
Answer:
b
Step-by-step explanation:
y
=
2
(
x
+
2
)
2
+
4
Use the vertex form,
y
=
a
(
x
−
h
)
2
+
k
, to determine the values of
a
,
h
, and
k
.
a
=2h
=
−
2
k
=
4
Find the vertex
(
h
,
k
)
.
(
−
2
,
4
)
image of graph

if the odds for a certain event are 7 to 17, what is the probability of the event occurring? write your answer as a simplified fraction.
Answers
The probability of the event occurring is 17/24
The meaning of "odds against of an event" :Odds in probability of a particular event, means the ratio between the number of outcomes of success to the number of outcomes of failure. It is denoted by x:y, and "x" is the number of outcomes of failure and y is the number of outcomes of success.
We have the information from the question is:
If the odds for a certain event are 7 to 17.
To find the probability of the event occurring.
Now,
Add the two numbers in the odds ratio together: 17 + 7 = 24.
Divide the number of favorable outcomes (17) by the total number of possible outcomes(24) : 17 ÷ 24.
Simplify the fraction, if possible.
The simplified fraction is 17/24.
Learn more about Probability at:
https://brainly.com/question/30034780
#SPJ4
How do you dilate points at a point?
Answers
To dilate a point at a point, you start by selecting a center of dilation and a scale factor.
Then, for each point that you want to dilate, you do the following:
Draw a line segment from the center of dilation to the point.Multiply the length of this line segment by the scale factor.Draw a line segment from the center of dilation to the new point, using the length that you just calculated.The new point is the point that you arrive at when you complete this line segment.For example, if you wanted to dilate point P by a scale factor of 2, with the center of dilation at O, you would draw a line segment from O to P, double its length, and then draw a new line segment from O to the new point, using the new length that you calculated. The new point would be the point that you arrive at when you complete this line segment.
Learn more about Scale Factor here:
https://brainly.com/question/25722260
#SPJ4
12 more than m machines
Answers
Answer:
m+12
Step-by-step explanation:
m+12
Solve for
�
cc.
Give an exact answer.
0.2
(
10
−
5
�
)
=
5
�
−
16
0.2(10−5c)=5c−16
Answers
The solution to the equation 0.2(10 - 5c) = 5c - 16 is c = 3.
To solve the equation 0.2(10 - 5c) = 5c - 16, we will first distribute the 0.2 on the left side of the equation:
0.2 * 10 - 0.2 * 5c = 5c - 16
Simplifying further:
2 - 1c = 5c - 16
Next, we will group the variables on one side and the constants on the other side by adding c to both sides:
2 - 1c + c = 5c + c - 16
Simplifying:
2 = 6c - 16
To isolate the variable term, we will add 16 to both sides:
2 + 16 = 6c - 16 + 16
Simplifying:
18 = 6c
Finally, we will divide both sides by 6 to solve for c:
18/6 = 6c/6
Simplifying:
3 = c
For more questions on equation
https://brainly.com/question/29174899
#SPJ8
The Six Sigma DMAIC approach is the best way to attack all problems and should be employed whenever possible. true or False?
Answers
False. The Six Sigma DMAIC approach is a problem-solving methodology used to improve processes and reduce defects, but it is not the only tool available.
What is Sigma?Sigma is a statistical measure of dispersion, which is used to measure the variability or spread of a given data set. It is calculated by taking the square root of the variance, which is the average of the squared differences from the mean. Sigma is commonly used in data analysis and is used to identify outliers and other patterns in data sets.
Depending on the nature of the problem, other problem-solving techniques may be more appropriate. For example, if the goal is to improve customer service, a method such as Lean Six Sigma, which focuses on customer value, may be more effective. Similarly, if the goal is to create new products or services, a design thinking approach could be used. In any case, it is important to assess the situation and choose the best course of action for the specific problem.
To know more about data set click-
https://brainly.com/question/14592520
#SPJ1
in frame of reference s, an electron moving along the x-axis has energy 4mc^2 what is the momentum magnitude observed in frame s'
Answers
The momentum magnitude observed in frame s' is √(15m^2c^4).
In special relativity, the relationship between energy (E) and momentum (p) is given by the equation:
E^2 = (pc)^2 + (mc^2)^2
where m is the rest mass of the particle, c is the speed of light, and p is the momentum of the particle.
In frame of reference s, the energy of the electron is given as 4mc^2. Plugging this into the equation, we have:
(4mc^2)^2 = (pc)^2 + (mc^2)^2
Simplifying this equation, we get:
16m^2c^4 = p^2c^2 + m^2c^4
Canceling out the common terms, we have:
15m^2c^4 = p^2c^2
Taking the square root of both sides, we get:
pc = √(15m^2c^4)
The momentum magnitude observed in frame s', denoted as p', is related to the momentum in frame s (p) by the relativistic velocity addition formula:
p' = γ(p - βE/c)
where γ is the Lorentz factor and β is the velocity of frame s' relative to frame s. Since the electron is moving along the x-axis, the velocity β is zero, and the Lorentz factor γ is equal to 1.
Therefore, the momentum magnitude observed in frame s' is the same as the momentum magnitude in frame s:
p' = p
Know more about momentum magnitude here:
https://brainly.com/question/14459931
#SPJ11
On a leveled ground, the base of a tree is 20m far from bottom of a 4. 8m long flagpole. At a certain time, their shadows end at the same point, which is 60m far from the base of the flagpole. Find the height of the tree
Answers
The height of the tree is 6.4m
the difference is that in one case the shadow of the tree is 60 - 20 = 40 m, and in the other case it is 60 + 20 = 80 m long.
anyway, for a certain angle of the sunlight we know the shadow of the pole is 60 m long, which creates with the 4.8 m height a right-angled triangle, with the line of sight from the top of the pole to the ground end of the shadow being the Hypotenuse or radius for or trigonometric triangle in a circle.
the shadow length (60 m) is sine of the sunshine angle multiplied by the radius.
the height (4.8 m) is cosine of that sunshine angle multiplied also by that radius.
Pythagoras gets us the radius for the pole triangle :
radius² = 60² + 4.8² = 3600 + 23.04 = 3623.04
radius = sqrt(3623.04) = 60.19169378... m
sin(angle) × radius = 60
sin(angle) = 60/radius = 0.996815279...
angle = 85.42607874...°
the sunshine creates with the tree also a right-angled triangle with the same sunshine angle (the sun is so far away, that the tiny, tiny difference is irrelevant, we can simply assume the angles are equal).
but the shadow is of different length (sin(angle)×radius), which means also the radius for the tree triangle has to be different. and that defines the height of the tree (cos(angle)×radius).
but now we know the angle, and we can reverse calculate the side lengths.
but the question is (as mentioned at the beginning) : is the tree shadow 40 m or 80 m long.
we have therefore 2 solutions for the height of the tree.
1. the shadow is 40 m long.
sin(angle) × radius = 40
radius = 40/sin(angle) = 40.12779585... m
tree height = cos(angle)×radius = 3.2 m
2. the shadow is 80 m long.
sin(angle) × radius = 80
radius = 80/sin(angle) = 80.25559171... m
tree height = cos(angle)×radius = 6.4 m
know more about height and distance click here;
https://brainly.com/question/15939509
#SPJ4
En una compañía se realiza una encuesta a 200 personas, se encontró la siguiente distribución, en el uso de máquinas eléctricas, mecánicas y computadoras: Eléctricas 110, mecánicas 50, computadoras 60. Mecánicas y computadoras 25, eléctricas y computadoras 35, eléctricas y mecánicas 40. Las tres 20 y 60 nada. A) Encuentre el número de personas que o usan computadora. B) Que usen una maquina eléctrica pero no computadora. C) Que usen solo un equipo. D) Que usen mecánica y eléctrica pero no computadora. E) Cuantos no tienen ni maquina eléctrica ni mecánica.
Answers
Answer:
A) 140
B) 75
C) 80
D) 20
E) 80
Step-by-step explanation:
Para resolver este problema debemos construir un diabrama de Venn y llenarlo según los datos que se nos brindan.
Comenzamos nombrando cada círculo:
E= personas que usan máquinas eléctricas
M= personas que usan máquinas mecánicas
C = personas que usan computadoras.
- Luego llenamos el área central con un 20, el cual representa las personas que usan los 3 tipos de maquinas.
- En la parte exterior del diagrama de Venn colocamos un 60 por las personas que no usan ninguna de las máquinas.
- En la intersección entre M y C restamos:
25-20=5
Entonces colocamos este 5 en esa región.
- En la intersección entre E y C restamos:
35-20=15
Entonces colocamos este 15 en esa región.
- En la intersección entre E y M restamos:
40-20=20
Entonces colocamos este 20 en esa región.
- En la región de E restamos:
110-20-20-15=55
Entonces colocamos este 55 en esa región.
- En la región de M restamos:
50-20-20-5=5
Entonces colocamos este 5 en esa región.
- En la región de C restamos:
60-15-20-5=20
Entonces colocamos este 20 en esa región.
Y obtenemos el diagrama de Venn que representa esta encuesta (Ver figura adjunta)
Y ahora ya lo podemos usar para responder a las preguntas:
A) Número de personas que no usan computadora. Sumamos los números fuera del círculo C:
55+20+5+60=140
B) Número de personas que usan una máquina eléctrica pero no computadora: Sumamos los números dentro del círculo E con excepción de los números compartidos por el círculo C y obtenemos:
55+20=75
C) Número de personas que usan solo un equipo: Sumamos los números no compartidos en los círculos E, M y C
55+20+5=80
D) Número de personas que usan máquina mecánica y eléctrica pero no computadora: Usamos el número compartido entre E y M que no son compartidos con C
20
E) Sumamos el número que se encuentra solo en C y los que están afuera del diagrama:
20´60=80

Complete the table to show how many ounces are equivalent to 6 pounds. Pounds 6 8 10 12 Ounces ? 128 160 192 There are ounces in 6 pounds.
Answers
Answer:
The answer is 12 pounds. i hope this helps! :)
Step-by-step explanation:
Answer:
96 ounces
Step-by-step explanation:
on edg! :)
Prisms that have 2400cm
Answers
Answer: A Rectangular prism
Plz help!!
If DF = 170, find the value of x. Then find DE and EF.

Answers
Answer
DE= 3x + 20 = 86EF= 2x + 40=84
Step-by-step explanation:
DE: 3x + 20
EF: 2x + 40
DE+ EF= DF
3x+20 +2x + 40 = 170
5x + 60 =170
5x= 110
x= 22
DE= 3x + 20 = 86EF= 2x + 40=84Answer:
x = 22
DE = 86
EF = 84
Step-by-step explanation:
DF=DE+EF
170= (3x +20) + ( 2x+40)
170 = 5x + 60
5x = 170 - 60
5x = 110
x = 110 / 5
x = 22
DE =3x + 20 = 3(22) + 20 = 66 + 20 = 86
EF= 2x + 40 = 2(22) + 40 = 44 + 40 = 84
I hope I helped you^_^
someone help me... please show work

Answers
Answer:
x=5
Step-by-step explanation:
Set the 2 equations equal to each other and solve for x.
11x-28=7x-8
add 28 to both sides (-8+28=20)
11x=7x+20
subtract 7x from both sides (11x-7x=4x)
4x=20
divide both sides by 4 to isolate x (20/4=5)
x=5