for the logistic function f(x)=100/(1 5(0.8)^-x) what is the value of the y-intercept
Answers
The value of the y-intercept for the logistic function f(x) = 100/(1 + 5(0.8)^-x) is 16.67.
The y-intercept of a function represents the point where the graph of the function intersects the y-axis. At the y-intercept, the value of x is 0. To find the y-intercept of the given logistic function, we can substitute x = 0 into the equation and simplify.
f(0) = 100 / (1 + 5(0.8)^0) = 100 / 6 = 16.67
Therefore, the y-intercept of the logistic function f(x) = 100/(1 + 5(0.8)^-x) is 16.67. This means that the graph of the function will intersect the y-axis at the point (0, 16.67).
The logistic function is commonly used to model growth or decay that starts slowly, increases rapidly, and then levels off over time. The denominator of the function, 1 + 5(0.8)^-x, ensures that the function approaches 100 as x increases without bound. The constant 100 represents the maximum possible value of the function.
The y-intercept represents the initial value of the function when x = 0, which is the starting point for the growth or decay modeled by the function. In the case of the logistic function, the initial value is 16.67, which means that the growth or decay starts at a relatively low level before accelerating and eventually leveling off.
You can learn more about y-intercept at
https://brainly.com/question/25722412
#SPJ11
Related Questions
James wants to buy a new cell phone package there are three packages available for each offering a different deal which package offers the best deal
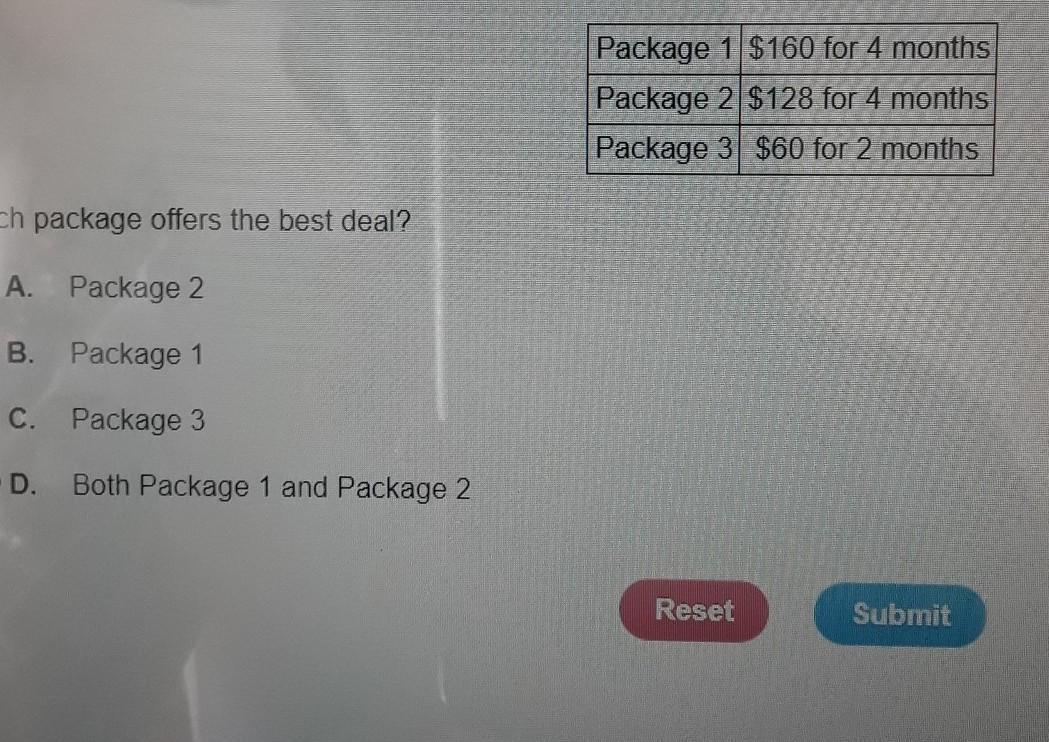
Answers
Answer:package 3
Step-by-step explanation:
Hope I am right it is there cheapest
please help meh i dont know the answer

Answers
He already had 220 so subtract that from how much the thing costs.
499 - 220 = 279
He gets 25 for every weekend so divide 279 by 25
279 divided by 25 = 11.16
Round it to 11.
I think that’s right, it’s been awhile since I’ve done math like this
Identify all the key features of the following quadratic function.

Answers
The key features of the function are
Axis of symmetry: x = -2Domain: -∝ < x < ∝Range: y ≥ - 6Vertex = (-2, 6)How to determine the key features of the function?The graph represents the given parameter of this question
From the question, the attached function is a quadratic function, and the key feature to calculate for the graph are:
DomainRangeVertexAxis of symmetryGenerally, the domain of a quadratic function is the set of all real values
This means that
Domain: -∝ < x < ∝
Also, the vertex from the graph is
Vertex = (-2, 6)
This represents the minimum
Remove the x coordinate
So, we have
y = -6
The vertex is a minimum
So, the range is y ≥ - 6
Recall that
Vertex = (-2, 6)
Remove the y coordinate
So, we have
x = -2
This represents the axis of symmetry
Read more about key features at
https://brainly.com/question/28614856
#SPJ1
What could be the value of x in the number sentence? 6 + x < 10
Answers
Answer:
the answer is 3 or less dhevvshsbdvdd
I'll give 16 points

Answers
Answer:
Arisa walks dog 3 for 15 min, dog 4 20 mins
Sofias dog 3 12 mins, dog 4 16 mins.
Step-by-step explanation:
Given the triangle ABC at points A = ( 2, 2 ) B = ( 4, 5 ) C = ( 6, 3 ), and if the triangle is first reflected over the y axis, and then over the x axis, find the new point A''.
Answers
Given
The triangle ABC at points A = (2, 2) B = (4, 5) C = (6, 3).
To find:
Solve the problem using graphical approximation techniques on a graphing calculator. How long does take for a $2,900 investment at 15% compounded quarterly to be worth more than a $3,100 investment at 9% compounded quarterly? Identify the formula required to solve this problem. A. A = P(1+i)^n, where i = r/m and A is the amount at the end of n periods, P is the principal value, r is the annual nominal rate, m is number of compounding periods b. I = Prt, where i = compounding periods m O B. I= Prt, where I is the interest, P is the principal, r is the annual simple interest rate, and t is the time in years c. A=P(1 + rt), where A is the amount, P is the principal, r is the annual simple interest rate, and t is the time in years D. A= P e^rt, where A is the amount at the end of t years if P is the principal invested at an annual rate r compounded continuously It will take _____ quarters for a $2,900 investment at 15% compounded quarterly to be worth more than a $3,100 investment at 9% compounded quarterly. (Round up to the nearest integer.)
Answers
It will take 16 quarters for a $2,900 investment at 15% compounded quarterly to be worth more than a $3,100 investment at 9% compounded quarterly.
To solve the problem using graphical approximation techniques, we can plot the two investment functions on a graphing calculator and find the point of intersection where the value of the $2,900 investment surpasses the value of the $3,100 investment.
Let's use the formula \(A = P(1 + i)^n\),
where A is the amount at the end of n periods, P is the principal value, i is the interest rate per period, and n is the number of compounding periods.
For the $2,900 investment at 15% compounded quarterly:
P = $2,900
i = 15% = 0.15/4
= 0.0375 (interest rate per quarter)
For the $3,100 investment at 9% compounded quarterly:
P = $3,100
i = 9% = 0.09/4
= 0.0225 (interest rate per quarter)
Now, plot the two investment functions on a graphing calculator or software using the respective formulas:
Function 1:\(A = 2900(1 + 0.0375)^n\)
Function 2:\(A = 3100(1 + 0.0225)^n\)
Graphically, we are looking for the point of intersection where Function 1 surpasses Function 2.
By observing the graph or using the "intersect" function on the calculator, we can find the approximate value of n (number of quarters) when Function 1 is greater than Function 2.
Let's assume the graph shows the intersection point at n = 15.6 quarters. Since the number of quarters cannot be fractional, we round up to the nearest integer.
Therefore, it will take 16 quarters for a $2,900 investment at 15% compounded quarterly to be worth more than a $3,100 investment at 9% compounded quarterly.
To know more about investment visit:
https://brainly.com/question/15105766
#SPJ11
which of the following equations represents the graph? pls help!

Answers
Answer:
H
Step-by-step explanation:
The answers simplify to:
F) y=2.5x+5
G) y= -5/2x+5
H) y=5/2x+5
J) y= 5/2x-5
Use rise/run to find slope
5/2=slope
y-intercept= 5
Your answer is H
Find the angle between vector bold lower u equals 3 bold lower I plus start root 3 end root bold lower j and vector bold lower v equals negative 2 bold lower I minus 5 bold lower j to the nearest degree. A. 82° B. 38° C. 142° D. 98°
Answers
Answer:
C. 142°
Step-by-step explanation:
You want the angle between vectors u=3i+√3j and v=-2i-5j.
AngleThere are a number of ways the angle between the vectors can be found. For example, the dot-product relation can give you the cosine of the angle:
u•v = |u|·|v|·cos(θ) . . . . . . where θ is the angle of interest
You can find the angles of the vectors individually, and subtract those:
u = |u|∠α
v = |v|∠β
θ = α - β
When the vectors are expressed as complex numbers, the angle between them is the angle of their quotient:
\(\dfrac{\vec{u}}{\vec{v}}=\dfrac{|\vec{u}|\angle\alpha}{|\vec{v}|\angle\beta}=\dfrac{|\vec{u}|}{|\vec{v}|}\angle(\alpha-\beta)=\dfrac{|\vec{u}|}{|\vec{v}|}\angle\theta\)
This method is used in the calculation shown in the first attachment. The angle between u and v is about 142°.
A graphing program can draw the vectors and measure the angle between them. This is shown in the second attachment.
__
Additional comment
The approach using the quotient of the vectors written as complex numbers is simply computed using a calculator with appropriate complex number functions. There doesn't seem to be any 3D equivalent.
The dot-product relation will work with 3D vectors as well as 2D vectors.
<95141404393>


find the circumference of a circle with a radius of 12ft
Answers
Answer
74.40
Step-by-step explanation:
circumference= 2πr
so, 12×2×pi= 24π
24π= 75.39822369
=75.40
the graph of y=x2(x 5) and y= 3 x (x>0) intersect at one point, x=r, as shown to the right. use newton's method to estimate the value of r.
Answers
Using Newton's method, the estimated value of r, the intersection point of the graphs of \(y = x^2(x - 5)\) and y = 3x, is approximately 1.2869.
To estimate the value of r using Newton's method, we need to find the root of the equation \(f(x) = x^2(x - 5) - 3x = 0\). We can start with an initial guess, let's say x_0 = 1.
Newton's method iteration formula is given by:
\(x_{(n+1)} = x_n - f(x_n)/f'(x_n)\)
First, let's find the derivative of f(x):
\(f'(x) = 3x^2 - 10x + 3\)
Using the initial guess x_0 = 1, we can iteratively apply the Newton's method formula to refine the estimate of r:
Iteration 1:
\(x_1 = x_0 - f(x_0)/f'(x_0)\)
\(= 1 - (1^2(1 - 5) - 3(1)) / (3(1)^2 - 10(1) + 3)\)
= 1 - (-3) / (-4)
= 1 + 3/4
= 5/4
= 1.25
Iteration 2:
x_2 = x_1 - f(x_1)/f'(x_1)
= 1.25 - (1.25^2(1.25 - 5) - 3(1.25)) / (3(1.25)^2 - 10(1.25) + 3)
≈ 1.2872
Continuing this process, we can perform more iterations to refine the estimate of r.
Iteration 3:
x_3 ≈ 1.2869
Iteration 4:
x_4 ≈ 1.2869
\(= 1.25 - (1.25^2(1.25 - 5) - 3(1.25)) / (3(1.25)^2 - 10(1.25) + 3)\)
mate of r converges to approximately 1.2869.
To know more about intersection point,
https://brainly.com/question/30927431
#SPJ11
to make 5 blueberry pies mindy needs about 2 pounds of blueberries how many pounds of blueberries does mindy need to make 20 blueberry pies
Answers
Answer:
8lbs
Step-by-step explanation:
5 pies = 2lbs
multiply both by 4 because you're making 4 times as many pies so
5x4=20
2x4=8
so she will need about 8 lbs of blueberries
A population has a mean μ=135 and a standard deviation Ï=28. Find the mean and standard deviation of the sampling distribution of sample means with sample size n=57.
Answers
A population has a mean μ=135 and a standard deviation Ï=28.
The mean of the sampling distribution of sample means is equal to the population mean, that is 135.
The standard deviation of the sampling distribution of sample means can be calculated by using the formula
SE = Ï /\(\sqrt{n}\)
Where Ï is the population standard deviation and n is the sample size.
By putting the given values we get
SE = 28 / \(\sqrt{57}\) = 3.7
Hence, the mean of the sampling distribution of sample means is 135, and the standard deviation is 3.7.
To know more about standard deviation here
https://brainly.com/question/28075377
#SPJ4
Jack ran a distance represented by the expression 3x + 7. Jill ran a distance represented by the expression 9x + 21. Which describes how the distance that Jill ran compares to the distance that Jack ran?
Answers
Answer:3(3x+7) -22 I'm pretty sure it's is 9x-1
Step-by-step explanation:
i will make you Brainliest if you know what fraction is equal to 1.5
Answers
Answer:
3/2
Step-by-step explanation:
There are a lot of fractions that equal 1.5, but if you're asking for the most simplified fraction, 3/2 is the answer.
3 step problems.....
Answers
Submarine 1 : at 4,863 feet and is ascending 81.1 feet per minute
Submarine 2: at 3,645 feet and is ascending 76.9 feet per minute
so, step 1:
The third statement is the true
Step 2:
For the same depth
-4,863 + 81.1 m = -3,645 + 76.9 m
solve to find m
so,
81.1 m - 76.9 m = 4863 - 3645
4.2 m = 1,218
m = 1,218/4.2 = 290 minutes
==============================================================================
Select all of the zeros of the function f(x)=(3x−4)(x+2).
(I NEED TO SHOW MY WORK SO PLEASE SHOW HOW YOU GOT THE ANWSER)
Select all that apply:
4
2
43
− 43
− 2
− 4
Answers
Answer:
The zeros of the function are x = 4/3 or x = -2
Step-by-step explanation:
To find the zeros of the function, we set f(x) to zero
Thus;
(3x-4)(x + 2) = 0
3x - 4 = 0
or x + 2 = 0
3x = 4 or x = -2
x = 4/3 or x = -2
Select the values below that are not equivalent to 72%
A.0.72
B. 72%
C. 3 72 / 100 - 3
D. 36/50
E. 72
F. 1 - 0.28
Answers
Answer:
Step-by-step explanation:
The values that are not equivalent to 72% are:
C. 3 72 / 100 - 3
D. 36/50
F. 1 - 0.28
On a trip, you had to change your money from dollars to British pounds. You got 560 pounds for 800 dollars. How many pounds will you get for 300 dollars?

Answers
Answer:
210 pounds
Step-by-step explanation:
First, we are going to find the exchange rate from dollars to pounds.
We know form our problem that 800 dollars are 560 pounds. so:
\frac{560pounds}{800dollars} =0.7
800dollars
560pounds
=0.7 pounds per dollar.
Next, we are going to multiply our exchange rate by the number of dollars we want to change, 300:
300dollars*\frac{0.7pounds}{dollar} =210pounds300dollars∗
dollar
0.7pounds
=210pounds
We will get 210 pounds for 300 dollars
c) at a certain event, 45 people attend, and 5 will be chosen at random to receive door prizes. the prizes are all the same, so the order in which people are chosen does not matter. [3 marks] how many different groups of five people can be chosen?
Answers
The different groups of five people chosen from 45 people by applying combination is equal to 1,221,759.
Total number of people = 45
Number of people chosen at random to receive door prize = 5
The number of different groups of five people that can be chosen out of 45 attendees,
we need to use the combination formula,
ⁿCₓ = n! / (x! × (n-x)!)
where n is the total number of attendees,
x is the number of people to be chosen,
and ! denotes factorial (e.g., 5! = 5 x 4 x 3 x 2 x 1).
Here, we have n = 45 and x = 5, so we can plug these values into the formula,
⁴⁵C₅
= 45! / (5! × (45-5)!)
= (45 x 44 x 43 x 42 x 41) / (5 x 4 x 3 x 2 x 1)
= 1,221,759
Therefore, there are 1,221,759 different groups of five people that can be chosen from a total of 45 attendees using combination.
learn more about combination here
brainly.com/question/27410240
#SPJ4
Simplify the expression by adding like terms: 5a-3+5b+20-a-2b
I need help with this!!
Answers
Add the like variables
Step-by-step explanation:
4a+3b+17
is your answer
hear is your explanation

the soccer field at bianca’s school has a length of 120 yards and a width of 85 yards. if she runs across the diagonal from one corner to another, how far does she run, in yards? round your answer to the nearest tenth.
Answers
The distance that she runs from one corner of the field to another is given as follows:
147.1 yards.
What is the Pythagorean Theorem?The Pythagorean Theorem states that for a right triangle, the length of the hypotenuse squared is equals to the sum of the squared lengths of the sides of the triangle.
The distance in this problem is the diagonal of a rectangle, which is the hypotenuse of a right triangle in which the length and the width are the sides, hence:
d² = 85² + 120²
d = sqrt(85² + 120²)
d = 147.1 yards.
More can be learned about the Pythagorean Theorem at brainly.com/question/30203256
#SPJ1
I’m kinda stuck on this, could anyone explain it ?

Answers
The slope of the given line is -3/4.
Any line perpendicular to this one will have slope -1/(-3/4) = 4/3.
Use the given point and the point-slope formula to get the equation of the particular line:
y - (-1) = 4/3 * (x - 0)
y + 1 = 4x/3
y = 4x/3 - 1
M/4=-13
Find the value of M?
Answers
Explanation:
1/4m =-13 covert 4 into a fraction
M=-52 you multiple both sides by 4 giving you -52
Hope this helps!!
The population of fish in a farm-stocked lake after t years could be modeled by the equation.
P(t( = 1000/1+9e-0.6t (a) Sketch a graph of this equation. (b) What is the initial population of fish?
Answers
(a) The graph of the given equation\(P(t) = 1000/1 + 9e^(-0.6t)\) can be drawn using the following steps. Step 1: Plot the point (0, 100) which is the initial population of fish. Step 2: Choose some values for t and find out the corresponding values of P(t). Step 3: Plot the ordered pairs obtained from the values of t and P(t).Step 4: Connect the plotted points to obtain the graph of the equation.
(b) We are given the population equation for a farm-stocked lake as P(t) = 1000/1 + 9e^(-0.6t). In order to find the initial population of fish, we substitute t = 0 in the given equation. \(P(0) = 1000/1 + 9e^(0)\)
= 1000/10
= 100.
The initial population of fish is 100.
To know more about ordered pairs visit:
https://brainly.com/question/30805001
#SPJ11
christine has 4 burger patties in her freezer. At the store, she can buy packs of 6 patties. She wants to have atleast 40 patties for the party. Write an inequality to represent the situation. What is the least number of whole packs Christine needs to buy for the party?
Answers
Answer:
4+6p ≥ 40
or simplified : 6p ≥ 36
She needs at least 6 packs.
Step-by-step explanation:
The amount of patties she has needs to be greater than 40, and she already has 4 in her freezer. So these 4 added to how many she buys at the store (which come in packs of 6) have to be greater than 40.
Divide 6 on both sides using the simplified version, p ≥ 6.
The graph of y = x^2 - 1/x^3 has a relative minimum at x = -√6
√6
-√3
√3
Answers
The second derivative is negative, at x = \(\sqrt[5]{- 3/2}\) is a relative maximum. Therefore, none of the answer choices given are correct.
We have to given that,
Equation of the graph is,
⇒ y = x² - 1/x³
Now, For the relative minimum of the function y = x - 1/x, we need to take its derivative and set it equal to zero as,
⇒ y = x² - 1/x³
⇒ y' = 2x + 3/x⁴
⇒ 2x + 3/x⁴ = 0
Solve for x,
⇒ 2x⁵ + 3 = 0
⇒ 2x⁵ = - 3
⇒ x⁵ = - 3/2
⇒ x = \(\sqrt[5]{- 3/2}\)
Now, we need to check whether this point is a relative minimum or maximum.
For this, at the sign of the second derivative:
y'' = 2 - 12/x⁵
At x = \(\sqrt[5]{- 3/2}\), we have:
y'' = 2 - 12/( \(\sqrt[5]{- 3/2}\))⁵
y'' = -8.42
Since, the second derivative is negative, we know that x = \(\sqrt[5]{- 3/2}\) is a relative maximum. Therefore, none of the answer choices given are correct.
Learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ4
I lost my notes for these and I am not good at remembering

Answers
Answer: 1, 4, and 5 are 125
2, 3, 6, 7 are 55
Step-by-step explanation:
1 and 8 are congruent by opposite exterior angles and I forgot how to explain 4 and 5 but you know 7 is 55 because a straight line is 180 degrees so is you subtract 125 (8) you get 55 (7)
The left and right ends of the normal probability distribution extend indefinitely, never quite touching the horizontal axis. True False
Answers
It is false as the left and right ends of the normal probability distribution extend indefinitely, approaching but never touching the horizontal axis.
The statement is false because the left and right ends of the normal probability distribution do not extend indefinitely. In reality, the normal distribution is defined over the entire real number line, meaning it extends infinitely in both the positive and negative directions. However, as the values move further away from the mean (the center of the distribution), the probability density decreases. This means that although the distribution approaches but never touches the horizontal axis at its tails, the probability of observing values extremely far away from the mean becomes extremely low. Thus, while the distribution theoretically extends infinitely, the practical probability of observing values far from the mean decreases rapidly.
To know more about normal probability distribution,
https://brainly.com/question/33601330
#SPJ11
Janet had 20 dollars to spend on 3 gifts. She spent 11 7/10 dollars on gift A and 4 2/5 dollars on gift B. How much money did she have left for gift C?