F(x)=4x+5whsts the value of. F(-3). Is
Answers
Answer:
F(-3) = -7
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDASAlgebra I
Function NotationStep-by-step explanation:
Step 1: Define
F(x) = 4x + 5
F(-3) is x = -3
Step 2: Evaluate
Substitute: F(-3) = 4(-3) + 5Multiply: F(-3) = -12 + 5Add: F(-3) = -7Related Questions
given the following venn diagram, where a and b are each represented by an oval: exam image which regions make up ( aexam imagebc )c?
Answers
The correct answer is U - II = I + III + IV.
In order to solve problems based on these sets, we can use a Venn diagram to depict the logical relationship between sets and their components. Although other closed figures like squares may be used, a Venn diagram commonly uses intersecting and non-intersecting circles to indicate the relationship between sets.
c represent the compliment of the particular state.
U is the union set
∩ represent intersection between the neighbouring sets
Therefore,
Bc = U - B = I + II
Bc∩A = Area common in Bc and A = II
(Bc∩A)c = Area in U but not in (Bc∩A) = U - II = I + III + IV
So, answer is d.
To learn more about the intersection click here:
brainly.com/question/14217061
#SPJ4
If f(x)=x² – 4x, what is the value of 2f(a-1)?
Answers
The correct value of 2f(a-1) is 2a^2 - 12a + 10.
To find the value of 2f(a-1), we need to substitute (a-1) into the function f(x) and then multiply the result by 2.
Given: f(x) = x^2 - 4x
Substituting (a-1) into the function:
f(a-1) = (a-1)^2 - 4(a-1)
Expanding and simplifying:
f(a-1) = (a^2 - 2a + 1) - (4a - 4)
f(a-1) = a^2 - 2a + 1 - 4a + 4
f(a-1) = a^2 - 6a + 5
Now, we multiply the result by 2:
2f(a-1) = 2(a^2 - 6a + 5)
Expanding:
2f(a-1) = 2a^2 - 12a + 10
Therefore, the value of 2f(a-1) is 2a^2 - 12a + 10.
Learn more about function here:
https://brainly.com/question/782311
#SPJ8
A.) (5,8)B.) (-7,-7)C.) (6,-3)D.) (4,4)Are the available options, thank you for the help.

Answers
We can find the point that is a solution to this system of linear equations by looking at the shaded region of the graph and determining which of the following points is included inside the shaded region.
By looking at the graph, we can determine that (5,8), (-7,-7), and (6,-3) are not part of the shaded region.
The point (4,4) is the only point that is included in the shaded region, inclusive on the red line.
Therefore, D) (4,4) is a solution to this system of linear inequalities.
How many degrees is the measure of ∠4
∠
4
?
Two parallel lines, P and Q, cut by two transversals, R and S. Together, angles four, an angle with measure 60 degrees, and an angle with measure 61 degrees, form a straight angle along line Q.
Answers
The measure of the angle m∠4 which forms a straight line angle with the angles 60° and 61° along the line Q is equal to 59°
What are angles formed by a pair of parallel lines cut by a transversal line?When a transversal line cuts a pair of parallel lines, several angles are formed which includes: Corresponding angles, vertical angles, alternate angles, complementary and supplementary angles.
m∠4 + 60° + 61° = 180° {supplementary angles}
m∠4 + 121° = 180°
m∠4 = 180° - 121° {subtract 121° from both sides}
m∠4 = 59°.
Therefore, the measure of the angle m∠4 which forms a straight line angle with the angles 60° and 61° along the line Q is equal to 59°
Read more about angles here:https://brainly.com/question/24607467
#SPJ1
After Verifying that the functions 1 2 satisfy the corresponding homogeneous equation of the given equation, find a particular solution of the non-homogeneous equation and then the general solution of the equation .
x²y'' + xy' + (x² - 0.25 ) y = 3x √xsinx
x> 0
y1(x) = sin (x) / √x
y2(x) = cos (x) / √x
Answers
To find a particular solution of the non-homogeneous equation and the general solution of the equation, we can use the method of variation of parameters.
First, let's find the Wronskian of the homogeneous solutions y1(x) and y2(x):
W(y1, y2) = | y1 y2 |
| y1' y2' |
We have y1(x) = sin(x) / √x and y2(x) = cos(x) / √x. Differentiating these functions, we get:
y1'(x) = (cos(x) / √x - sin(x) / (2√x^3))
y2'(x) = (-sin(x) / √x - cos(x) / (2√x^3))
Substituting these values into the Wronskian:
W(y1, y2) = | sin(x) / √x cos(x) / √x |
| (cos(x) / √x - sin(x) / (2√x^3)) (-sin(x) / √x - cos(x) / (2√x^3)) |
Expanding the determinant:
W(y1, y2) = (sin(x) / √x) * (-sin(x) / √x - cos(x) / (2√x^3)) - (cos(x) / √x) * (cos(x) / √x - sin(x) / (2√x^3))
Simplifying:
W(y1, y2) = -1 / (2√x)
Now, we can find the particular solution using the variation of parameters formula:
y_p(x) = -y1(x) * ∫(y2(x) * g(x)) / W(y1, y2) dx + y2(x) * ∫(y1(x) * g(x)) / W(y1, y2) dx
Here, g(x) = 3x√xsin(x). Substituting the values:
y_p(x) = -((sin(x) / √x) * ∫((3x√xsin(x)) * (-1 / (2√x))) dx + (cos(x) / √x) * ∫((3x√xsin(x)) / (2√x)) dx
Simplifying the integrals:
y_p(x) = -(∫(-3sin^2(x)) dx) + (∫(3xcos(x)sin(x)) dx)
Integrating:
y_p(x) = 3/2 (xsin^2(x) - cos^2(x)) - 3/2 (xcos^2(x) + sin^2(x)) + C
Simplifying:
y_p(x) = 3x(sin^2(x) - cos^2(x)) + C
The general solution of the equation is given by the sum of the homogeneous solutions and the particular solution:
y(x) = C1 * (sin(x) / √x) + C2 * (cos(x) / √x) + 3x(sin^2(x) - cos^2(x)) + C
where C1, C2, and C are arbitrary constants.
A round pencil is sharpened to a cone shape at both ends.calculate the volume of the pencil if the two radius is 1.2 and heights are 8cm
Answers
Answer:
A round pencil is sharpened at both ends the hight of the pencil is 16cm the length of the pencil is 1cm the radius of the two sharpened ends is 16cm 1.2cm
Calculate the volume using the value 22/7.
Step-by-step explanation:
A person standing on a moving walkway travles 90 feet in 30 seconds what equation represents this relationship? how many feet will the person travle in 10 seconds?
Answers
Answer:B
Step-by-step explanation:y=3x;30 feet
how do you solve 5/13y+25=0
Answers
Answer:
y = -100/13
Step-by-step explanation:
To solve this equation, we can first get all the terms containing the variable y on one side of the equation and all the constant terms on the other side. We can do this by subtracting 25 from both sides of the equation:
5/13y + 25 - 25 = 0 - 25
This gives us:
5/13y = -25
Next, we can divide both sides of the equation by 5/13 to get rid of the fraction:
(5/13y) / (5/13) = (-25) / (5/13)
This simplifies to:
y = -100/13
Therefore, the solution to the equation is y = -100/13.
Evaluate the expression 6^2-(8–4^2+7
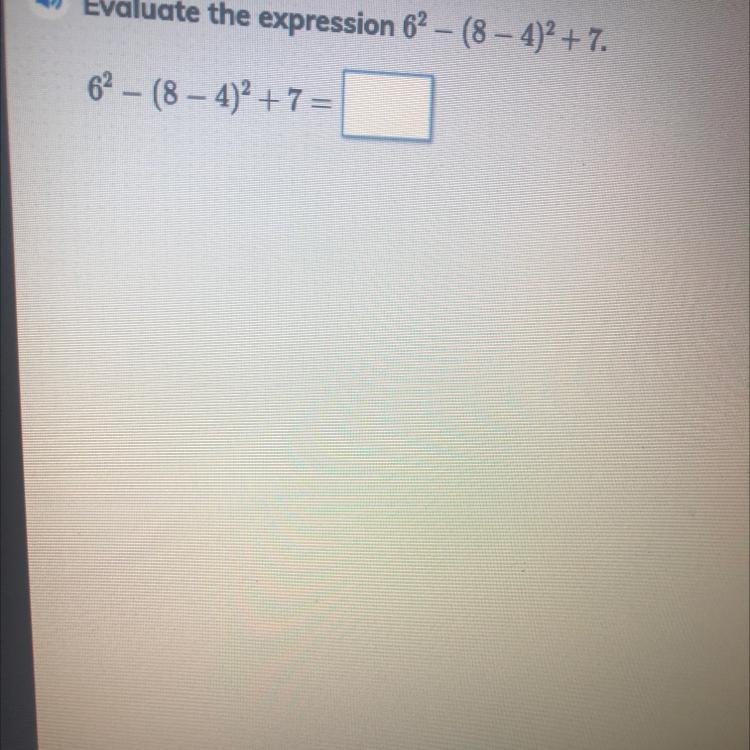
Answers
please mark this answer as brainlist
The value of given expression is 27.
What is an expression?An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division.
The given expression is 6²-(8-4)²+7.
Here, 6²-(8-4)²+7
= 6²-(4)²+7
= 36-16+7
= 20+7
= 27
Therefore, the value of given expression is 27.
To learn more about an expression visit;
https://brainly.com/question/28170201.
#SPJ2
Can u please help I will do Brainleyist

Answers
Answer:
the answer is B this other guy messed up his math trust me i know it's right
Step-by-step explanation:
if you add up all the numbers it equals 27 squar units
Which is the completely factored form of 18x4 – 42x3 + 24x2?
3x(3x - 4)(2x - 2)
3x2(3x - 4)(2x - 2)
6x(3x – 4)(x - 1)
6x²(3x - 4)(x - 1)
Answers
Answer:
D
Step-by-step explanation:
The completely factored form is 6x² (3x - 4) (x - 1).
Option D is the correct answer.
What is an expression?An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
18\(x^4\)– 42x³ + 24x²
Now,
The common factor of 18, 42, and 24 is 6.
And x² is common to all the terms.
So,
6x² (3x²– 7x + 4) _____(1)
Now,
(3x²– 7x + 4)
3x² - (4 + 3)x + 4
3x² - 4x - 3x + 4
x(3x - 4) - 1(3x - 4)
(3x - 4) (x - 1) ______(2)
Now,
From (1) and (2) we get,
6x² (3x - 4) (x - 1)
Thus,
6x² (3x - 4) (x - 1) is the completely factored form.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ6
. Which of the following is the maximum value of the equation y = −x2 − x + 6?
Answers
Answer:
x=6-x2-y
Step-by-step explanation:
Swap sides so that all variable terms are on the left hand side.
add x2 to both side
Subtract 6 from both sides.
Divide both sides by −1.
Dividing by −1 undoes the multiplication by −1.
Divide y+x2 −6 by −1.
prove :
sin²θ + cos²θ = 1
thankyou ~
Answers
Answer:
See below
Step-by-step explanation:
Here we need to prove that ,
\(\sf\longrightarrow sin^2\theta + cos^2\theta = 1 \)
Imagine a right angled triangle with one of its acute angle as \(\theta\) .
The side opposite to this angle will be perpendicular . Also we know that ,\(\sf\longrightarrow sin\theta =\dfrac{p}{h} \\\)
\(\sf\longrightarrow cos\theta =\dfrac{b}{h} \)
And by Pythagoras theorem ,
\(\sf\longrightarrow h^2 = p^2+b^2 \dots (i) \)
Where the symbols have their usual meaning.
Now , taking LHS ,
\(\sf\longrightarrow sin^2\theta +cos^2\theta \)
Substituting the respective values,\(\sf\longrightarrow \bigg(\dfrac{p}{h}\bigg)^2+\bigg(\dfrac{b}{h}\bigg)^2\\\)
\(\sf\longrightarrow \dfrac{p^2}{h^2}+\dfrac{b^2}{h^2}\\ \)
\(\sf\longrightarrow \dfrac{p^2+b^2}{h^2} \)
From equation (i) ,\(\sf\longrightarrow\cancel{ \dfrac{h^2}{h^2}}\\ \)
\(\sf\longrightarrow \bf 1 = RHS \)
Since LHS = RHS ,
Hence Proved !
I hope this helps.
Scott has 2 six-sided dice. What is the probability that the sum of the roll is one?
Answers
Answer: 0, it’s not possible to roll 2 dice with the sum ending up being one.
When x > 0 and y > 0, what expression is equivalent to √180x^9y^16 in simplest form?
Answers
Answer:
\(6x^4y^8\sqrt{5x}\)
Step-by-step explanation:
\(\textsf{When $x > 0$ and $y > 0$, we want to find the expression that is equivalent to}\) \(\sqrt{180x^9y^{16}}.\)
\(\textsf{First, apply the radical rule:} \quad \sqrt{ab}=\sqrt{a}\sqrt{b}\)
\(\sqrt{180}\sqrt{x^9}\sqrt{y^{16}}\)
\(\textsf{Rewrite $x^9$ as $x^{8+1}$:}\)
\(\sqrt{180}\sqrt{x^{(8+1)}}\sqrt{y^{16}}\)
\(\textsf{Apply the exponent rule:} \quad a^{b+c}=a^b \cdot a^c\)
\(\sqrt{180}\sqrt{x^{8}\cdot x^1}\sqrt{y^{16}}\)
\(\sqrt{180}\sqrt{x^{8}}\sqrt{x}\sqrt{y^{16}}\)
\(\textsf{Apply\:the\:radical\:rule:\:}\sqrt[n]{a^m}=a^{\frac{m}{n}},\:\quad a\geq 0\)
\(\sqrt{180}\;x^{\frac{8}{2}}\sqrt{x}\;y^{\frac{16}{2}}\)
\(\sqrt{180}\;x^4\sqrt{x}\;y^8\)
\(\sqrt{180}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Rewrite $180$ as $(6^2 \cdot 5)$:}\)
\(\sqrt{6^2 \cdot 5}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Apply the radical rule:} \quad \sqrt{ab}=\sqrt{a}\sqrt{b}\)
\(\sqrt{6^2} \sqrt{5}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Apply the radical rule:} \quad \sqrt{a^2}=a, \quad a \geq 0\)
\(6 \sqrt{5}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Apply the radical rule:} \quad \sqrt{a}\sqrt{b}=\sqrt{ab}\)
\(6 \sqrt{5x}\;x^4\;y^8\)
\(\textsf{Rearrange:}\)
\(6x^4y^8\sqrt{5x}\)
\(\textsf{Therefore, when $x > 0$ and $y > 0$, the expression that is equivalent to}\)
\(\sqrt{180x^9y^{16}}\;\textsf{is}\;\;\boxed{6x^4y^8\sqrt{5x}}\:.\)
Which is the best first step when solving the following system of equations?
x+y=3
4x-y=7
O Multiply the first equation by 4.
Add the first equation to the second equation.
Multiply the second equation by -1.
Subtract the second equation from the first equation.
Answers
The best first step to solve equations, x+y = 3 and 4x-y = 7, is to add the first equation to the second equation.
According to the question,
We have the following system of equations:
x+y = 3 .....(1)
4x-y = 7 ....(2)
Now, these equations can be easily solved by adding the first equation to the second equation because we will only then have one variable which is x and y when added to -y will result in zero.
We can solve these equations by adding as follows:
x-y+4x+y = 3+7
5x = 10
x = 10/5
x = 2
Now, we can put the value of x in equation 1 to find the value of y:
2+y = 3
y = 3-2
y = 1
Hence, the correct option is B.
To know more about first step to solve equations here
https://brainly.com/question/24160452
#SPJ1
A rectangular prism has a length of 714 inches, a width of 612 inches, and a height of 10 inches.
Raj has another prism that has dimensions that are each double the dimensions of the first rectangular prism.
How many times greater is the volume of the larger prism than the volume of the smaller one?
Answers
Answer:
8 timesStep-by-step explanation:
The volume of the prism:
V = lwhIf each of the dimensions is doubled, then the volume becomes:
V₁ = 2l*2w*2h = 8lwh = 8VThe larger prism has 8 times greater volume
so can u help me guys

Answers
Thus, 715,000 = 7.15 x 10⁵, using the concept of scientific notations, both the values are found to be equal.
Explain about the scientific notations:The number of times that decimal point must be moved to obtain a number between 1 and 10 is the exponent in scientific notation. The decimal point is shifted to the left in order to represent this number in scientific notation.
The main goal of scientific notation is to simplify computations using numbers that are abnormally large or small. With scientific notation, every digit counts because zeros are just no longer used to denote the decimal point.
Given expression:
715,000 __ 7.15 x 10⁵
LHS = 715,000
Take the RHS value :
= 7.15 x 10⁵
This, can be simplifies as:
= 7.15 x 100,000
Now multiply the two values,
= 715,000 (RHS values)
as, LHS = RHS
LHS = 715,000
715,000 (RHS values)
Thus, 715,000 = 7.15 x 10⁵, using the concept of scientific notations, both the values are found to be equal.
Know more about the scientific notations:
https://brainly.com/question/1767229
#SPJ1
A spinner with 6 colors is spun and a number cube is tossed determine the number of outcomes
Answers
Answer:
36
Step-by-step explanation:
since there are six outcomes for the spinner and six outcomes for the cube,
6 x 6 = 36
A tank is full of water. Find the work required to pump the water out of the spout. Use the fact that water weighs 62.5 lb/ft3. (Assume r = 6 ft, R = 12 ft, and h = 16 ft.)
A tank is full of water. Find the work
required toThe answer should be (number pi J )
Answers
The work required to pump the water out of the spout is 12,249.7 pi J.
Let's assume that the radius of the tank is 6 ft, the radius of the spout is 12 ft, and the height of the water in the tank is 16 ft.
To calculate the work required to pump the water out of the spout, we'll need to use the equation: W = (4/3)πr2(h+R-r) ρg where W is the work required, π is pi (3.1415), r is the radius of the tank, R is the radius of the spout, h is the height of the water in the tank, and ρg is the density of water (62.5 lb/ft3).
Plugging in our values, we get:
W = (4/3)π(6 ft)2(16 ft + 12 ft - 6 ft) (62.5 lb/ft3)
W = (4/3)π(36 ft2) (34 ft) (62.5 lb/ft3)
W = (4/3)π(2268 ft3) (62.5 lb/ft3)
W = 12,249.7 pi J
Therefore, the work required to pump the water out of the spout is 12,249.7 pi J.
Learn more about work done:
brainly.com/question/21854305
#SPJ4
Write 5/6% as a decimal number.
Answers
Answer: 5/6 as a decimal is 0.833
Step-by-step explanation:
just divide 5 by 6
What is a correct definition of P-value?
Answers
p-value is a measure of the probability that an observed difference could have occurred just by random chance.
1 is subtracted from 8 times a certain number.the result is 15.find the number
Answers
Answer:
number is 2
Step-by-step explanation:
let the number be n then 8 times the number is 8n, subtract 1 from this and
8n - 1 = 15 ( add 1 to both sides )
8n = 16 ( divide both sides by 8 )
n = 2
that is the number is 2
Helpp please I don’t understand :(

Answers
Answer:
s = 2 1/3 + 1/2
t = 2/3 + 3/2
We have to find the sum of both s and t.
2 1/3 + 1/2 = 2 2/6 + 3/6 = 2 5/6
2/3 + 3/2 = 4/6 + 9/6 = 13/6 = 2 1/6
If we look at the number lines, we can see that c matches with both points.
write 1,340 in scientific notatin
Answers
1340 = 1.34 x 10^3
Remember that scientific notation has a number between 1 and 10 multiplied by 10 to a certain power. To find the exponent, count the number of times you moved the decimal point.
Hope this helps!! :)
Janine inflated a ball to a radius of 18cm and another ball to a radius of 12cm. how much greater was the volume of air in the larger ball than the smaller ball?
Answers
Answer:
17,190.79 cm ³
Step-by-step explanation:
24429.02 - 7238.23
Find the quotient of 3/5 3/7. Write your answer in the simplest form.
Answers
\(\cfrac{3}{5}\div\cfrac{3}{7}\implies \cfrac{~~\begin{matrix} 3 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}{5}\cdot \cfrac{7}{~~\begin{matrix} 3 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}\implies \cfrac{7}{5}\implies 1\frac{2}{5}\)
Which polynomial is prime?
O 3x³ + 3x² - 2x - 2
O 3x³ − 2x² + 3x − 4
-
O
4x³ + 2x² + 6x + 3
O
4x³+4x²-3x - 3

Answers
Answer:
B
Step-by-step explanation:
a prime polynomial is one which does not factor into 2 binomials.
its only factors are 1 and itself
attempt to factorise the given polynomials
3x³ + 3x² - 2x - 2 ( factor the first/second and third/fourth terms )
= 3x²(x + 1) - 2(x + 1) ← factor out common factor (x + 1) from each term
= (x + 1)(3x² - 2) ← in factored form
--------------------------------------------------
3x³ - 2x² + 3x - 4 ( factor the first/second terms
= x²(3x - 2) + 3x - 4 ← 3x - 4 cannot be factored
thus this polynomial is prime
----------------------------------------------------
4x³ + 2x² + 6x + 3 ( factor first/second and third/fourth terms )
= 2x²(2x + 1) + 3(2x + 1) ← factor out common factor (2x + 1) from each term
= (2x + 1)(2x² + 3) ← in factored form
-------------------------------------------------
4x³ + 4x² - 3x - 3 ( factor first/second and third/fourth terms )
= 4x²(x + 1) - 3(x + 1) ← factor out common factor (x + 1) from each term
= (x + 1)(4x² - 3) ← in factored form
--------------------------------------------------
the only polynomial which does not factorise is
3x³ - 2x² + 3x - 4
Gillian has completed 25% of a bicycle race. If the length of the race is 32 km, how many has she traveled so far?
800
80
8
8000
NO LINKS
Answers
Answer:
8 km
Step-by-step explanation:
0.25 x 32 = 8
If these cylinders and prisms were broken into two separate groups, what would be an equivalent ratio to 8/2? i dont have much longer and btw it doesn't have a picture.
100 points?
Answers
The Equivalent ratio to 8/2 is 4/1, 24/6, 32/8 and 48/12.
We have,
Cylinder and prism.
Here we have to find the equivalent ratio to 8/2.
First simplifying the given ratio as
8/2
= (4 x 2)/2
= 4 /1
Now, some more ratios equivalent to 8/2.
1. 8/2 x 3/3 = 24/ 6
2. 8/2 x 4/4 = 32/8
3. 8/2 x 6/6= 48/12
Learn more about Ratio here:
https://brainly.com/question/13419413
#SPJ1