Given XY = 15, WX = 22, ZX = 52, WT = 23, m
ZW =
m
ZY =
m
TX =
m
WY =
m
Answers
ZW is 37 units long. By subtracting the length of WY, which is found to be -1, from ZW, we found that ZY is 38 units long. However, the lengths of TX and WY are negative, suggesting a potential error in the given information.
In the given figure, we are provided with the lengths of various line segments. Using this information, we can determine the length of ZW. Given that XY = 15 and ZX = 52, we can subtract the length of XY from ZX to find the length of ZW. Therefore, ZW = ZX - XY = 52 - 15 = 37.
Now let's provide a detailed explanation of each length:
ZY = 37
To find the length of ZY, we need to subtract the length of WY from ZW. From the previous calculation, we know that ZW = 37. However, the length of WY is not given directly. To find it, we can use the fact that WX = 22 and WT = 23. Since WY is a part of WX and WT, we can subtract WT from WX to get WY. Therefore, WY = WX - WT = 22 - 23 = -1.
Now, we can substitute the value of WY into the equation for ZY: ZY = ZW - WY = 37 - (-1) = 38. Thus, ZY is equal to 38.
TX = 15
To find the length of TX, we need to subtract the length of WT from XY. We know that XY = 15 and WT = 23. Therefore, TX = XY - WT = 15 - 23 = -8. However, it is important to note that lengths cannot be negative, so TX cannot be -8. This indicates that there might be an error in the given information or measurements.
WY = -1
As calculated earlier, the length of WY is -1. However, it is important to note that lengths cannot be negative in a geometrical context. Therefore, we can conclude that there might be an error in the given information or measurements. It is advisable to double-check the given lengths or clarify any inconsistencies before proceeding with further calculations.
In summary, using the given information, we determined that ZW is 37 units long. By subtracting the length of WY, which is found to be -1, from ZW, we found that ZY is 38 units long. However, the lengths of TX and WY are negative, suggesting a potential error in the given information. It is recommended to verify the measurements to ensure accurate results.
Learn more about length here
https://brainly.com/question/28322552
#SPJ11
Related Questions
show work
Question 17 41 Consider the following hypothesis test: Claim: o> 2.6 Sample Size: n = 18 Significance Level: a = 0.005 Enter the smallest critical value. (Round your answer to nearest thousandth.)
Answers
The smallest critical value is 2.898.
Given the sample size, n = 18, the significance level, a = 0.005, and the claim is o > 2.6.
To find the smallest critical value for this hypothesis test, we use the following steps:
Step 1: Determine the degrees of freedom, df= n - 1= 18 - 1= 17
Step 2: Determine the alpha value for a one-tailed test by dividing the significance level by 1.α = a/1= 0.005/1= 0.005
Step 3: Use a t-table to find the critical value for the degrees of freedom and alpha level. The t-table can be accessed online, or you can use the t-table provided in the appendix of your statistics book. In this case, the smallest critical value corresponds to the smallest alpha value listed in the table.
Using a t-table with 17 degrees of freedom and an alpha level of 0.005, we get that the smallest critical value is approximately 2.898.
Therefore, the smallest critical value is 2.898 (rounded to the nearest thousandth).
To know more about critical value visit:
https://brainly.in/question/33583755
#SPJ11
Alex walks 2/3 mile in 1/4 hour. What is Alex's unit rate in miles per hour?
Answers
Answer:
8mph
Step-by-step explanation:
2 miles ÷ 0.25
0.25 hours ÷ 0.25
8/1
Please help quickly!!
A truck is driving up a hill with a 24% grade, so it climbs 24 feet vertically for every 100 feet horizontally.
What is the slope of the hill?
Answers
Answer:
6/25
Step-by-step explanation:
rise / run
24/100 = 6/25
Answer:
\(\frac{6}{25}\)
Step-by-step explanation:
The slope of any relationship is always rise over run. This means the vertical distance traveled over the horizontal distance traveled will get us our slope.
We travels 24 feet vertically for every 100 feet horizontally, so:
\(\frac{24}{100}\).
We can simplify this fraction to find the slope in fraction form.
\(\frac{24\div4}{100\div4} = \frac{6}{25}\)
So the slope of this equation is \(\frac{6}{25}\).
Hope this helped!
x - 3 < 4
graph the inequality
Answers
Answer: See the image below.

what is the best big-o function for the worst case scenario analysis of a linar search of a list of size n (counting the number of comparisons)?
Answers
Big O notation focuses on the worst-case scenario analysis, which is 0(n) for a simple search. It’s a reassurance that a simple search will never be slower than O(n) time.
Imagine that you're a teacher with a student named Ram. You want to find his records, so you use a simple search algorithm to go through your school district's database.
You know that a simple search takes O(n) times to run. This means in the worst case, you'll have to search through every single record to find Ram
After a simple search, you find that Ram records are the very first entry in the database. You don't have to look at every entry.
Did this algorithm take O(n) time Or did it take O(1) time because you found Ram records on the first try?
In this case, 0(1) is the best-case scenario – you were lucky that Ram records were at the top. But Big O notation focuses on the worst-case scenario, which is 0(n) for a simple search. It’s a reassurance that a simple search will never be slower than O(n) time.
Learn more about Big-o from
https://brainly.com/question/13257594
#SPJ4
PLEASE HELPPP!!
Find the value of X.

Answers
Combine like terms
6x + 91.5 = 180
Subtract 91.5 from both sides
6x = 88.5
Divide by 6
X = 14.75
The answer is 3) 14.75
A recipe for crumb cake says to mix 3/8 cup of brown sugar and 1/3 cup of white sugar.
From this sugar mixture, set aside 1/4 cup for the crumb topping.
The remaining sugar mixture is used to make the cake.
What amount of the sugar mixture is used to make the cake?
A.) 17/24
B.) 11/24
C.) 1/2
D.) 7/12
Answers
Answer:
C) 1/2
Step-by-step explanation:
We know that 3/8 cup of brown sugar and 1/3 cup of white sugar are mixed together to make the sugar mixture.
From this sugar mixture, 1/4 cup is set aside for the crumb topping.
To find out how much sugar mixture is used to make the cake, we need to subtract the amount set aside for the crumb topping from the total sugar mixture.
We can start by converting the mixed unit of measurement (brown sugar in cups and white sugar in cups) to a single unit of measurement (cups)
3/8 cup of brown sugar + 1/3 cup of white sugar = (3/8)+(1/3) = 5/12 cup + 4/12 cup = 9/12 cup.
1/4 cup is set aside for the crumb topping.
So, the remaining sugar mixture used to make the cake is 9/12 cup - 1/4 cup = (9/12) - (1/4) = (9-3)/12 = 6/12 cup = 0.5 cup
Brittany needed new tires for her truck. She went to the auto shop and brought 4 tires on sale for $85.95 each. The salesman told her that she saved a total of $96.16. If Brittany saved the same amount on each tire, what was the original price for each tire?
Answers
Answer:
109.99
Step-by-step explanation:
Take the amount saved and divide by 4 to find the amount saved on each tire
96.16/4 =24.04
Add that to the sale price of each tire to find the original price
85.95+24.04 =109.99
The original price is 109.99
Answer:
109.99
Step-by-step explanation:
cuz physics
There are 116 pieces of fruit in the box. There are 10 less apples than oranges. Find the number of
apples and oranges.
Answers
Answer:
53, 63
Step-by-step explanation:
added in the picture

30 identical sticks lined up in a row and five of them are to be chosen. how many choices are there if no two of the chosen sticks are consecutive?
Answers
The number of choices when choosing five sticks from a row of 30 with no two consecutive sticks is C(30,5) - C(29,3) which is equal to 3,628 choices.
The formula used to calculate the number of choices when choosing five sticks from a row of 30 with no two consecutive sticks is C(30,5) - C(29,3).
C(30,5) is a combination formula which calculates the number of possible combinations for 30 items taken five at a time. This formula would give us the total number of possible combinations of five sticks.
C(29,3) is another combination formula which calculates the number of possible combinations for 29 items taken three at a time. This formula gives us the number of combinations in which three consecutive sticks are chosen.
Therefore, the number of choices when choosing five sticks from a row of 30 with no two consecutive sticks is C(30,5) - C(29,3) which is equal to 3,628 choices.
Learn more about combinations here:
https://brainly.com/question/20211959
#SPJ4
3. Use the either the sum or difference formula of cosine to solve the following (5 points) cos(525 degrees)
Answers
By using the sum or difference formula of cosine to solve cos(525°) we get cos(525°) = -0.465
The formula to find the value of cos(A ± B) is given as,
cos(A + B) = cosA cosB − sinA sinBcos(A − B) = cosA cosB + sinA sinB
Here, A = 450° and B = 75°
We can write 525° as the sum of 450° and 75°.
Therefore,cos(525°) = cos(450° + 75°)
Now, we can apply the formula for cos(A + B) and solve it.
cos(A + B) = cosA cosB − sinA sinBcos(450° + 75°) = cos450° cos75° − sin450° sin75°= 0.707 × 0.259 − 0.707 × 0.966= -0.465
Substituting the values in the above equation, we get
cos(525°) = 0.707 × 0.259 − 0.707 × 0.966= -0.465
Thus, cos(525°) = -0.465.
To know more about cosine visit:
brainly.com/question/29114352
#SPJ11
According to a particular marketing corporation,the per capita consumption of bottled water is 3.4 gallons per month Assume the standard deviation for this population is 0.85 gallons per month Consider a random sample of 100 people. a.What is the probability that the sample mean will be less than 33 gallons per month? b.What is the probability that the sample mean will be more than 3.6 gallons per month? c.ldentify the symmetrical interval that includes 93% of the sample means if the true population mean is 3.4 gallons permonth a.The probability that the sample mean will be less than 3.3 gallons per month is Type an integer or decimal rounded to four decimal places as needed
Answers
The symmetrical interval that includes 93% of the sample means is (3.2455 gallons per month, 3.5545 gallons per month) assuming the population follows a normal distribution.
To calculate the probabilities and identify the symmetrical interval, we'll use the provided information:
Given:
Population mean (μ) = 3.4 gallons per month
Population standard deviation (σ) = 0.85 gallons per month
Sample size (n) = 100
a. Probability that the sample mean will be less than 3.3 gallons per month: To calculate this probability, we need to use the sampling distribution of the sample mean, assuming the population follows a normal distribution. Since the sample size (n) is large (n > 30), we can approximate the sampling distribution as a normal distribution using the Central Limit Theorem. The mean of the sampling distribution is equal to the population mean (μ), which is 3.4 gallons per month. The standard deviation of the sampling distribution, also known as the standard error (SE), can be calculated as σ / √n:
SE = σ / √n
= 0.85 / √100
= 0.085 gallons per month
Now, we can calculate the z-score using the formula:
z = (x - μ) / SE
Substituting the values:
z = (3.3 - 3.4) / 0.085
= -0.1 / 0.085
= -1.1765
Using a standard normal distribution table or calculator, we can find the probability corresponding to a z-score of -1.1765. The probability that the sample mean will be less than 3.3 gallons per month is approximately 0.1190. Therefore, the probability is 0.1190.
b. Probability that the sample mean will be more than 3.6 gallons per month:
Similarly, we can calculate the z-score for this case:
z = (x - μ) / SE
= (3.6 - 3.4) / 0.085
= 0.2 / 0.085
= 2.3529
Using a standard normal distribution table or calculator, we find the probability corresponding to a z-score of 2.3529. The probability that the sample mean will be more than 3.6 gallons per month is approximately 0.0096.
Therefore, the probability is 0.0096.
c. Identifying the symmetrical interval that includes 93% of the sample means:
To find the symmetrical interval, we need to determine the z-scores corresponding to the tails of 93% of the sample means.
Since the distribution is symmetrical, we can divide the remaining probability (100% - 93% = 7%) equally between the two tails.
Using a standard normal distribution table or calculator, we find the z-score corresponding to a tail probability of 0.035 on each side. The z-score is approximately 1.8125.
The symmetrical interval is then given by:
=μ ± z * SE
=3.4 ± 1.8125 * 0.085
=(3.4 - 1.8125 * 0.085, 3.4 + 1.8125 * 0.085)
=(3.4 - 0.1545, 3.4 + 0.1545)
=(3.2455, 3.5545)
To know more about symmetrical interval,
https://brainly.com/question/32624935
#SPJ11
Amy is a stockbroker. She receives a commission based on the value of the trades she makes. If she earns a $50 commission for sales of $1,000, what is her percent of commission?
Answers
The percent of commission if Amy If she earns a $50 commission for sales of $1,000 is 5%.
Percentage commissionThis is a fee charged by an agent or broker for carrying out a transaction.
For instance, a reseller's commission:
The real-estate broker charged a four percent commission for their knowledge on bidding for commercial properties; for their intellectual perspective on making a formal offer and the strategy to obtain a mutually satisfying deal with the seller in favour of the buyer.
Amount of commission = $50Total sales = $1,000Percent commission = Amount of commission / Total sales × 100
= 50 / 1000 × 100
= 0.05 × 100
Percent commission = 5%
Therefore, the percent of commission if Amy If she earns a $50 commission for sales of $1,000 is 5%.
Learn more about percent commission:
https://brainly.com/question/26283663
#SPJ1
Find the H.C.F. of 567 and 255 using Euclid’s division lemma.
Answers
Step-by-step explanation:
To find the Highest Common Factor (H.C.F.) of 567 and 255 using Euclid's division lemma, we can follow these steps:
Step 1: Apply Euclid's division lemma:
Divide the larger number, 567, by the smaller number, 255, and find the remainder.
567 ÷ 255 = 2 remainder 57
Step 2: Apply Euclid's division lemma again:
Now, divide the previous divisor, 255, by the remainder, 57, and find the new remainder.
255 ÷ 57 = 4 remainder 27
Step 3: Repeat the process:
Next, divide the previous divisor, 57, by the remainder, 27, and find the new remainder.
57 ÷ 27 = 2 remainder 3
Step 4: Continue until we obtain a remainder of 0:
Now, divide the previous divisor, 27, by the remainder, 3, and find the new remainder.
27 ÷ 3 = 9 remainder 0
Since we have obtained a remainder of 0, the process ends here.
Step 5: The H.C.F. is the last non-zero remainder:
The H.C.F. of 567 and 255 is the last non-zero remainder obtained in the previous step, which is 3.
Therefore, the H.C.F. of 567 and 255 is 3.
11/13 x 3/22 reduce all answers to their lowest term
Answers
Answer:
3/26
Step-by-step explanation:
Simplified
Al released his balloon from the 10-yard line, and it landed at the 16-yard line. If the ball reached a height of 27 yards, what equation represents the path of his toss?
Answers
The equation of the path of the parabola is y = a(x - 13)² + 27
Given data ,
To represent the path of Al's toss, we can assume that the path is a parabolic trajectory.
The equation of a parabola in vertex form is given by:
y = a(x - h)² + k
where (h, k) represents the vertex of the parabola
Now , the balloon was released from the 10-yard line and landed at the 16-yard line, we can determine the x-values for the vertex of the parabola.
The x-coordinate of the vertex is the average of the two x-values (10 and 16) where the balloon was released and landed:
h = (10 + 16) / 2 = 13
Since the height of the balloon reached 27 yards, we have the vertex point (13, 27)
Now, let's substitute the vertex coordinates (h, k) into the general equation:
y = a(x - 13)² + k
Substituting the vertex coordinates (13, 27)
y = a(x - 13)² + 27
To determine the value of 'a', we need another point on the parabolic path. Let's assume that the highest point reached by the balloon is the vertex (13, 27).
This means that the highest point (13, 27) lies on the parabola
Substituting the vertex coordinates (13, 27) into the equation
27 = a(13 - 13)² + 27
27 = a(0) + 27
27 = 27
Hence , the equation representing the path of Al's toss is y = a(x - 13)² + 27, where 'a' can be any real number
To learn more about parabola click :
https://brainly.com/question/24042022
#SPJ1
Determine which of the points (−4,5), (4,3), and (1,2) lie on both the lines −x1−4x2=−16 and −3x1−5x2=−13.
Answers
The only point that lies on both lines is (-4,5).
To determine which of the points (−4,5), (4,3), and (1,2) lie on both the lines −x1−4x2=−16 and −3x1−5x2=−13, we need to check if the coordinates of each point satisfy both of the equations.
For the first line, we can rewrite it as x2 = (-x1 + 16)/4 and for the second line, we can rewrite it as x2 = (-3x1 + 13)/5.
Substituting the coordinates of each point into these equations, we get:
For the point (-4,5):
-4(2) + 16/4 = -4 + 4 = 0, and
-3(-4) + 13/5 = 12/5 + 13/5 = 25/5 = 5.
Therefore, (-4,5) satisfies both equations.
For the point (4,3):
4(2) + 16/4 = 8 + 4 = 12, and
-3(4) + 13/5 = -12 + 13/5 = -47/5.
Therefore, (4,3) does not satisfy both equations.
For the point (1,2):
-1(2) + 16/4 = -2 + 4 = 2, and
-3(1) + 13/5 = -3 + 13/5 = 2/5.
Therefore, (1,2) does not satisfy both equations.
Therefore, the only point that lies on both lines is (-4,5).
When given two equations, the solution can be found by solving the system of equations. To solve a system of equations, one should find the values of x and y that satisfy both equations. The solution to the system is the point (x,y) that satisfies both equations.
Know more about "equations":-
https://brainly.com/question/14114409#
#SPJ11
an inverted pyramid is being filled with water at a constant rate of 55 cubic centimeters per second. the pyramid, at the top, has the shape of a square with sides of length 8 cm, and the height is 14 cm. find the rate at which the water level is rising when the water level is 6 cm.
Answers
The rate at which the water level is rising when the water level is 6 cm is approximately 2.67 cm/s. if an inverted pyramid is filled with water at a constant rate of 55 cubic centimeters per second, the top of pyramid is in square shape with length of 8 cm and height of 14 cm.
Let's call this rate "r".
Volume of pyramid = (1/3) * base area * height
Since the pyramid has a square base, the base area is given by
Base area = (side length)^2
Substituting the given values
Base area = (8 cm)^2 = 64 cm^2
Height = 14 cm
V = (1/3) * 64 cm^2 * 14 cm = 298.67 cm^3
We know that the water is being added to the pyramid at a constant rate of 55 cm^3/s. Therefore, the rate at which the volume is increasing is
dV/dt = 55 cm^3/s
We also know that the volume of water in the pyramid at any given time is given by
V_water = (1/3) * base area * h_water
where h_water is the height of the water at that time.
To find the rate at which the water level is rising (r), we need to find dh_water/dt. We can do this by taking the derivative of both sides of the equation for V_water with respect to time
dV_water/dt = (1/3) * base area * dh_water/dt
Substituting the known values
dV_water/dt = (1/3) * (8 cm)^2 * dh_water/dt
dV_water/dt = (64/3) cm^2 * dh_water/dt
dh_water/dt = 3 * dV_water/dt / 64
dh_water/dt = 3 * 55 cm^3/s / 64 = 2.67 cm/s
To know more about rate here
https://brainly.com/question/24020169
#SPJ4
∠A and \angle B∠B are vertical angles. If m\angle A=(3x+3)^{\circ}∠A=(3x+3) ∘ and m\angle B=(4x-8)^{\circ}∠B=(4x−8) ∘ , then find the value of x.
Answers
Answer:
The value of x is 11 degrees
Step-by-step explanation:
Here, given that two angles are vertical angles, we are interested in calculating the value of x. We simply want to use an important property of vertical angles to get the value of x as given in the question.
When we talk of vertical angles, they are angles which lies on opposite side to each other when we have two intersecting line.
By property, vertically opposite angles are equal.
Thus, in this case, we are to equate the angles we are having since they are both vertical angles;
Thus,
Mathematically;
angle A = angle B
3x + 3 = 4x -8
Collect like terms;
4x-3x = 3 + 8
x = 11 degrees
HELP PLEASE. I DONT KNOW IF ITS 30 OR 180

Answers
To see why, we can simplify √180 as follows:
√180 = √(36 × 5) (since 36 is a perfect square that can be factored out)
√180 = √36 × √5 (using the product rule of square roots)
√180 = 6√5
Therefore, 6√5 is equivalent to √180.
Answer:
Step-by-step explanation:
6\(\sqrt{5\\\)
\(\sqrt{5*36}\)
\(\sqrt{180}\)
If you think about it logically, how can you take 6 out? So there was a number 36 under the root, and because of that there is a possibility to take it out, because 6 squared is 36
| 7 + m | - 4 > 8
A m > 9 or m < -15
B m > -2 or m < -20
C m > 5 or m < -19
D m > 7 or m < 0

Answers
Answer:
C m > 5 or m < -19
Step-by-step explanation:
i took the test
A triangle has sides with lengths of 100 inches, 56 inches, and 80 inches. Is it a right triangle?
Answers
Answer:
No.
Step-by-step explanation:
If these sides come out true in the Pythagorean Theorem, then it is a right triangle.
a² + b² = c²
56² + 80² = 100²
3136 + 6400 = 10000
9536 ≠ 10000
Since these values do not come out true in the Pythagorean Theorem, it is not a right triangle.
Answer:
Possibly, A right triangle has a really long side that is "c" in the picture. If the 100 length is c then the 80 one could be "b" while the 56 is "a"
I know it doesnt make much sense but I hope it helps
I see people looking at mine because its simple but you should look at the other guys awnser. He has information and details that explain their awnser. I didn't really do much to get the awnser. Look at theirs Please.

In the equation Y=13X+38 where Y is a function of X a) Y is a constant. b) 38 is a variable. c) the slope of the line is 13. d) None of these. 13) If Kolin catches 25 fish and gathers 70 fruits it would be co a) an efficient combination b) an unattainable combination c) an inefficient combination d) the most efficient combination Use the figure on the left to answer qucstions 14. 14. What is the equilibrium price and quantify? a. $35 and 6 dozens of roses per day b. $10 and 2 dozens of roses per day? c. Sis and 14 dozens of roses per day d. $25 and 10 dozens of roses per day
Answers
1)The slope of the line is C) 13. 2)It would be inefficient since it is not the most optimal use of resources.the correct option is C. 3)The equilibrium price and quantity are D) $25 and 10 dozens of roses per day, respectively.
1) Y = 13X + 38, where Y is a function of X.
The slope of the line is 13.
Therefore, the correct option is C.
2) Kolin catches 25 fish and gathers 70 fruits. If we consider the combination, then it would be inefficient since it is not the most optimal use of resources.
Therefore, the correct option is C.
3) Using the given figure, we can see that the point where the demand and supply curves intersect is the equilibrium point. At this point, the equilibrium price is $25 and the equilibrium quantity is 10 dozens of roses per day.
Therefore, the correct option is D. The equilibrium price and quantity are $25 and 10 dozens of roses per day, respectively.
Note that this is the point of intersection between the demand and supply curves, which represents the market equilibrium.
Know more about equilibrium price here,
https://brainly.com/question/29099220
#SPJ11
Please help, I am desperate!?! Will name Brainliest!!
Suppose that a spotlight is used for lighting objects at many different distances and that the area A of the light circle produced is related to the distance x to the lighted object by A=0.1x^2.
a. If the spotlight produces 250 lumens of light energy, what function gives the intensity of the light I, (in lumens per square foot) as a function of the distance x in feet from the spotlight to its target?
b. Write and solve equations that match these questions about the light intensity from the spotlight.
i. What is the intensity of light on an object that is 20 feet from the spotlight source?
ii. How far from the spotlight is an object that recieves 100 lumens of light per square foot?
Answers
Answer:
Intensity = 2500/x^2
6.25 lumem
5 Feets
Step-by-step explanation:
Given the following :
Area (A) = 0.1x^2
Intensity, Energy and Area are related by the formular :
Intensity = power / Area
A) If 250 lumens of light energy is produced :
Intensity (I) = 250 / 0.1x^2
Intensity = 2500/x^2
x = distance
B) USING THE EQUATION :
1) What is the intensity of light on an object that is 20 feet from the spotlight source?
x = 20
Intensity = 2500/x^2
Intensity = 2500/20^2
Intensity = 2500/400
Intensity = 6.25 lumen
11) How far from the spotlight is an object that recieves 100 lumens of light per square foot?
Intensity = 100
100 = 2500 / x^2
100x^2 = 2500
x^2 = 2500/ 100
x^2 = 25
x = 5 Feets
What is the slope of a line with the following coordinates: (2, 4) and (6, 12)
Answers
Answer:
y=2x
Step-by-step explanation:
> what do you get if you add −1/4 to itself four times? what is −1/4 × 4? are they the same? what should they be?
Answers
When you add -1/4 to itself four times, you get: -1
When you multiply -1/4 by 4, you also get: -1.
Yes, both the results are same which is: -1.
To answer your question, let's break it down into two parts:
1. What do you get if you add -1/4 to itself four times?
To find the answer, you simply add -1/4 four times:
(-1/4) + (-1/4) + (-1/4) + (-1/4) = -1
2. What is -1/4 × 4?
To multiply -1/4 by 4, you perform the multiplication:
(-1/4) × 4 = -1
In conclusion, when you add -1/4 to itself four times, you get -1, and when you multiply -1/4 by 4, you also get -1.
To know more about "Multiplication" refer here:
https://brainly.com/question/30597787#
#SPJ11
look at the given pattern carefully and complete the table.
plz say
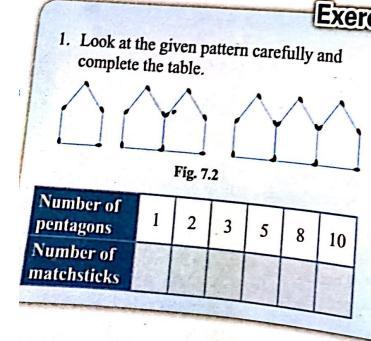
Answers
Answer:
#of pentagons | 1 | 2 | 3 | 5 | 8 | 10 |
#of matchsticks | 5| 9 | 13|21|33| 41 |
the equation for the question can also be written as x=the number of pentagons. m=the number of matchsticks. x*4+1=m
Step-by-step explanation:
plug in the number of pentagons for x and solve it and the number of matchsticks
Can someone help me with this Question.

Answers
The formula we need to use is given above. In this formula, we will substitute the desired values. Let's start.
\(P=3W+D\)A) First, we can start by analyzing the first premise. The team has \(8\) wins and \(5\) losses. It earned \(8 \times 3 = 24\) points in total from the matches it won and \(1\times5=5\) points in total from the matches it drew. Therefore, it earned \(24+5=29\) points.
B) After \(39\) matches, the team managed to earn \(54\) points in total. \(12\) of these matches have ended in draws. Therefore, this team has won and lost a total of \(39-12=27\) matches. This number includes all matches won and lost. In total, the team earned \(12\times1=12\) points from the \(12\) matches that ended in a draw.
\(54-12=42\) points is the points earned after \(27\) matches. By dividing \(42\) by \(3\) ( because \(3\) points is the score obtained as a result of the matches won), we find how many matches team won. \(42\div3=14\) matches won.
That leaves \(27-14=13\) matches. These represent the matches team lost.
Finally, the answers are below.
\(A)29\)
\(B)13\)
Answer:
a) 29 points
b) 13 losses
Step-by-step explanation:
You want to know points and losses for different teams using the formula P = 3W +D, where W is wins and D is draws.
A 8 wins, 5 drawsThe number of points the team has is ...
P = 3W +D
P = 3(8) +(5) = 29
The team has 29 points.
B 54 pointsYou want the number of losses the team has if it has 54 points and 12 draws after 39 games.
The number of wins is given by ...
P = 3W +D
54 = 3W +12
42 = 3W
14 = W
Then the number of losses is ...
W +D +L = 39
14 +12 +L = 39 . . . substitute the known values
L = 13 . . . . . . . . . . subtract 26 from both sides
The team lost 13 games.
__
Additional comment
In part B, we can solve for the number of losses directly, using 39-12-x as the number of wins when there are x losses. Simplifying 3W +D -P = 0 can make it easy to solve for x. (In the attached, we let the calculator do the simplification.)
<95141404393>

What is the median of the following set of numbers: 14, 17, 11, 17, 12, 13, 13, 14, 19, 25, 22, 18, 11, 23, 9
Answers
Answer:
9
Step-by-step explanation:
Answer:
14
Step-by-step explanation:
Arranging the numbers in ascending order,
9,11,11,12,13,13,14,14,17,17,18,19,22,23,25
Median = 14
Finding a Percent of a Number A 2-column table with 4 rows titled What after school activity do you participate in question mark. Column 1 has entries sport, club, extra help, none. Column 2 has entries 40 percent, 35 percent, 15 percent, 10 percent. The table shows the results of a survey about after-school activities. If 210 students participated in the survey, how many of those students do not participate in any after-school activities? students
Answers
Answer:
21 percent
Step-by-step explanation:
First, you have to divide 210 by 10 to get 21 percent. Plus I got it correct. Please mark me brainlest.
Answer: I'm Pretty Sure Its 21
Step-by-step explanation:
Hope this helps anybody