Hey, my sis can't register rn so I'm asking this question for her. She's learning PEMDAS and she was given 4 numbers, 18, 2, 3, and 4, and 3 symbols, ×, +, and ÷. She has to use PEMDAS and get to the number 12 at the end of it.
Answers
Answer:
(18 + 2 * 3) / 3 + 4
Step-by-step explanation:
If you can’t use parentheses,
here is another solution:
18 + 3*4 / 3 + 2
Related Questions
What’s 165 rounded to the nearest 10
Answers
Answer:
it would be 170 it its 5 or over round up
Step-by-step explanation:
The slope of the line below is -1/7. write a point slope equation of the line using the coordinates of the labeled point.

Answers
The equation of a straight line can be written if its slope and any one point lying on it is given. The equation of the line for given slope and point is (y - 3) = -1 / 7 × (x - 3). The correct answer is option B.
What is the equation for a straight line?A straight line can be written in the form of equation as, y = mx + c.
Two straight lines intersect each other only at one point.
When two straight lines are parallel to each other the angle between them is zero.
Given that,
The slope of the line = -1 / 7
The coordinate of the point on the line = (3,3)
The equation of a line having slope m and passing through a point (x₁, y₁) is given as,
(y - y₁) / (x - x₁) = m
Thus, the equation of the line for given slope and point is given as,
(y - 3) / (x - 3) = -1 / 7
=> (y - 3) = -1 / 7 × (x - 3)
Hence, the equation of the line for given slope and point is (y - 3) = -1 / 7 × (x - 3).
To know more about straight line equation click on,
https://brainly.com/question/21627259
#SPJ1
Concrete cement is being installed around a rectangular swimming pool that measures 10m by 5m. The cement will have a uniform width 4m all around the pool.
(a) Calculate the area surrounding the swimming pool.
(b) Cement costs $50 per m2 for material and labour. Determine the cost to install the cement.
Answers
(a) To calculate the area surrounding the swimming pool, we need to consider the width of the cement around all sides of the pool. Since the cement has a uniform width of 4m on all sides, we need to add 4m to the length and width of the pool.
The length of the pool with the surrounding cement is 10m + 2(4m) = 10m + 8m = 18m.
The width of the pool with the surrounding cement is 5m + 2(4m) = 5m + 8m = 13m.
The area surrounding the swimming pool is the difference between the area of the larger rectangle (with the cement) and the area of the pool itself.
Area surrounding pool = Area of larger rectangle - Area of pool
= (18m) x (13m) - (10m) x (5m)
= 234m² - 50m²
= 184m².
(b) The cost to install the cement is determined by multiplying the area surrounding the pool by the cost per square meter, which is $50.
Cost to install cement = Area surrounding pool × Cost per square meter
= 184m² × $50/m²
= $9,200.
More on area of rectangles can be found here: https://brainly.com/question/8663941
#SPJ1
What units would you use to describe the volume of a box measured in
centimeters?
A. Cubed centimeters
B. Inches
C. Square feet
D. Cubed Inches
Answers
Answer:
A
Step-by-step explanation:
If a=3+√7/2, then find the value of a²+1/a²
Answers
The value of a² + 1/a² is 17 - 7.5√7.
To find the value of a² + 1/a², let's first simplify the expression for a.
Given: a = (3 + √7) / 2
Now, let's square both sides of the equation to eliminate the square root:
a² = [(3 + √7) / 2]²
= (3 + √7)² / 4
= (9 + 6√7 + 7) / 4
= (16 + 6√7) / 4
= 4 + (6√7) / 4
= 1 + (3√7) / 2
Next, let's find the reciprocal of a:
1/a = 1 / [(3 + √7) / 2]
= 2 / (3 + √7)
= [2 * (3 - √7)] / [(3 + √7) * (3 - √7)]
= [6 - 2√7] / (9 - 7)
= [6 - 2√7] / 2
= 3 - √7
Now, let's square both sides of the equation to find the value of 1/a²:
(1/a)² = (3 - √7)²
= 9 - 6√7 + 7
= 16 - 6√7
Finally, we can calculate the value of a² + 1/a²:
a² + 1/a² = (1 + (3√7) / 2) + (16 - 6√7)
= 1 + 16 + (3√7) / 2 - 6√7
= 17 - (3√7) / 2 - 6√7
= 17 - (15√7) / 2
= 17 - 7.5√7.
For similar question on expression .
https://brainly.com/question/24734894
#SPJ11
Answer number 12 please thank you

Answers
Answer:
D. (A U C) ∩ B
Step-by-step explanation:
12.
A = {-2, -1, 0, 1}
B = {0, 1, 2, 3}
C = {-2, 0, 2, 4}
A. A U B = {-2, 1, 0 , 1, 2, 3}
B. A U (C ∩ B} = A U {0, 2} = {2, 1, 0, 1, 2}
C. B ∩ C = {0, 2}
D. (A U C) ∩ B = {-2, -1, 0, 1, 2, 4} ∩ {0, 1, 2, 3} = {0, 1, 2}
Given the following proposition:
[A ⊃ ~(B · Y)] ≡ ~[B ⊃ (X · ~A)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 1A
Answers
The truth value of Proposition 1, [A ⊃ ~(B · Y)] ≡ ~[B ⊃ (X · ~A)], is true when A and B are true, and X and Y are false.
First, we'll evaluate each part of the proposition:
1. A ⊃ ~(B · Y): Since A is true and B · Y is false (due to Y being false), the statement becomes "true ⊃ ~false", which simplifies to "true ⊃ true". This is true.
2. B ⊃ (X · ~A): Since B is true, X is false, and ~A is false, the statement becomes "true ⊃ (false · false)", which simplifies to "true ⊃ false". This is false.
Now, we'll evaluate the equivalence ([A ⊃ ~(B · Y)] ≡ ~[B ⊃ (X · ~A)]): The statement becomes "true ≡ ~false", which simplifies to "true ≡ true". Therefore, the truth value of Proposition 1 is true.
To know more about Proposition click on below link:
https://brainly.com/question/14789062#
#SPJ11
solve for f.
85+ f/8=91
Answers
Answer:
f=48
Step-by-step explanation:
Its correct good luck!
What 895 times 50??
(Only Answer If You Want Spam)
Answers
Answer:
44750
Step-by-step explanation:
In the diagram below of right triangle ABC, CD is the altitude to hypotenuse AB, CB = 6, and AD = 5.
What is the length of BD?
1) 5
2) 9
3) 3
4) 4

Answers
The value of BD in the similar triangle is 4 units.
How to find the side of a right triangle?A right angle triangle is a triangle that has one of its angles as 90 degrees. The triangles are similar .
Therefore, let's use the ratios of the similar triangle to find the side BD.
Let
BD = x
Therefore,
x / 6 = 6 / (5 + x)
cross multiply
x(x + 5) = 6 × 6
x² + 5x = 36
x² + 5x - 36 = 0
x² - 4x + 9x - 36 = 0
x(x - 4) + 9(x - 4) = 0
(x + 9)(x - 4) = 0
x = -9 or 4
Therefore, x(BD) can only be positive.
Hence,
BD = 4
learn more on triangle here: https://brainly.com/question/21552421
#SPJ1
Find the Surface area of the trapezoid
please help
show work

Answers
Answer:
259.5
Step-by-step explanation:
8.1*12=97.2
Area of trapiezium = 1/2(b+a)h
(2.8+8.1)=10.9
10.9*3/2=16.35
16.35*2=32.7
2.8*12=33.6
33.6+32.7+97.2=163.5
4*12*2=96
163.5+96=259.5
3 tons of topsoil cost 2,520.00. What is the price per pound?
Answers
Answer:
$0.42
Step-by-step explanation:
3ton=6000pounds
2,520/6000=$0.42
In a lab, a substance was heated by 6 Celsius each hour for 42 hours. What was the total change in temperature?
Answers
Answer: 7
Step-by-step explanation: 42 divided by 6 is 7.
Line BC is tangent to the circle centered at A. Find the measure of angle BCA. Explain or show your reasoning.
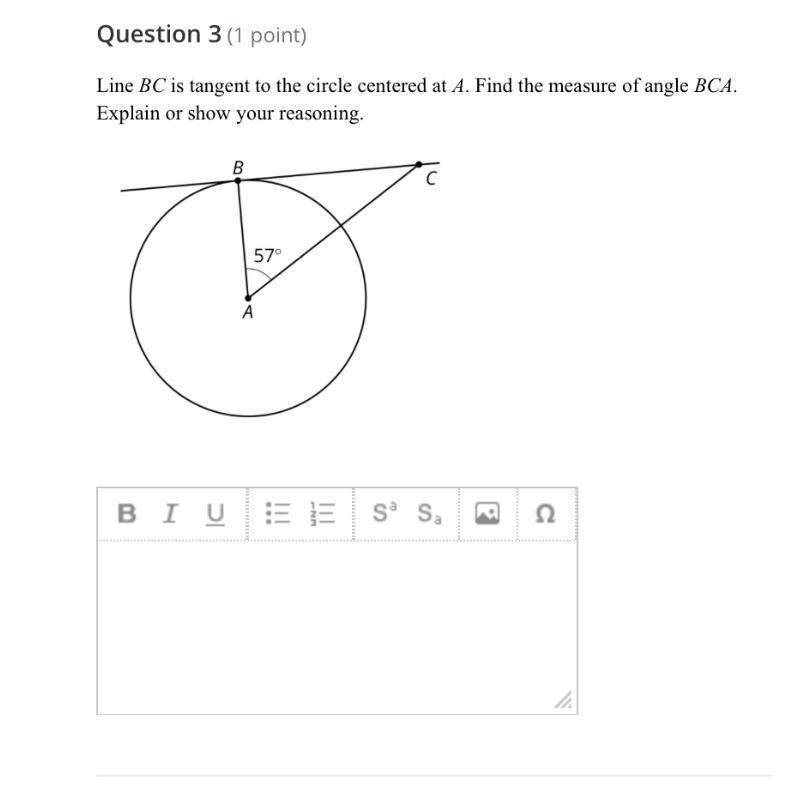
Answers
Answer:
\( m\angle BCA= 33\degree\)
Step-by-step explanation:
\( In\: \odot A\) BC is tangent to the circle at point B.
Therefore, by tangent-radius theorem:
\( \therefore AB\perp BC\)
\( \therefore \angle ABC = 90\degree \)
\( In\: \triangle ABC, \)
\( m\angle ABC +m\angle BAC +m\angle BCA= 180\degree \)
\( 90\degree+57\degree +m\angle BCA= 180\degree \)
\( 147\degree +m\angle BCA= 180\degree \)
\( m\angle BCA= 180\degree - 147\degree\)
\( m\angle BCA= 33\degree\)
What is an equation of the line that passes through the points (5,4) and (2,-2)?
Answers
Answer:
y = 2x − 6
Step-by-step explanation:
What is one way to simplify variables with many, many levels (or decimal places) when creating a frequency distribution?A. Ignore outliers B. Organize data into class intervals C. Graph each level of the variable individually D. Compute a mean, median, and mode
Answers
One way to simplify variables with many levels (or decimal places) when creating a frequency distribution is to organize the data into class intervals (option B).
By grouping the data into intervals, the frequency distribution becomes more manageable and easier to interpret. This process involves dividing the range of values into distinct intervals or categories and then counting the number of observations falling within each interval. Class intervals provide a summary of the data by grouping similar values together, reducing the complexity of individual levels or decimal places.
This simplification technique is particularly useful when dealing with large datasets or continuous variables that have numerous levels or decimal values, allowing for a clearer representation and analysis of the data.
Option B holds true.
Learn more about frequency distribution: https://brainly.com/question/27820465
#SPJ11
The graph represents the distribution of the lengths of play times, in minutes, for songs played by a radio station over one hour.
A graph shows the horizontal axis numbered 2.6 to x. The vertical axis is unnumbered. The graph shows an upward trend from 2.8 to 3.4 then a downward trend from 3.4 to 4.
Which statement is true about the songs played during the one-hour interval?
Most of the songs were between 3 minutes and 3.8 minutes long.
Most of the songs were 3.4 minutes long.
Most of the songs were less than 3.2 minutes long.
Most of the songs were more than 3.6 minutes long.
Answers
The correct statement is Most of the songs were between 3 minutes and 3.8 minutes long.
Based on the given information from the graph, we can determine the following:
The graph shows an upward trend from 2.8 to 3.4 on the horizontal axis.
Then, there is a downward trend from 3.4 to 4 on the horizontal axis.
From this, we can conclude that most of the songs played during the one-hour interval were between 3 minutes and 3.8 minutes long. This is because the upward trend indicates an increase in length from 2.8 to 3.4, and the subsequent downward trend suggests a decrease in length from 3.4 to 4.
Therefore, the correct statement is:
Most of the songs were between 3 minutes and 3.8 minutes long.
for such more question on minutes
https://brainly.com/question/25279049
#SPJ8
Answer:
A
Step-by-step explanation:
Can you please help me out with a question
Answers
a sphereical balloon is inflating with helium at a rate of 128pi ft^3/min. how fast is the balloon's radius increasing at the instant the radius is 4 ft
Answers
A sphereical balloon is inflating with helium at a rate of \(128\pi ft^3/min\).The balloon's radius is increasing at a rate of 8 ft/min when the radius is 4 ft.
To find the rate at which the balloon's radius is increasing, we can use the relationship between the volume of a sphere and its radius. The volume of a sphere is given by the formula V = (4/3)πr³, where V is the volume and r is the radius.
We are given that the volume is increasing at a rate of 128π ft³/min. Taking the derivative of the volume formula with respect to time, we have dV/dt = 4πr²(dr/dt), where dV/dt represents the rate of change of volume and dr/dt represents the rate of change of the radius.
At the instant when the radius is 4 ft, we can substitute r = 4 into the equation. Solving for dr/dt, we have 128π = 4π(4)²(dr/dt), which simplifies to dr/dt = 8 ft/min.
Therefore, the balloon's radius is increasing at a rate of 8 ft/min when the radius is 4 ft.
Learn more about volume here:
https://brainly.com/question/21623450
#SPJ11
Sandeep has s small spoons and 22 big spoons. Write an expression that shows how many spoons Sandeep has.
Answers
Answer: s + 22 is the answer.
if the angles (4x+4) and 6x-4 are supplement Ary angles find value of x plzz helppp
Answers
Angles (4x + 4°) and (6x - 4°) are supplementary.
That is :
\((4x + 4°) + (6x - 4°) = 180°\)Solution :\(\hookrightarrow \: 4x + 4 \degree + 6x -4 \degree = 180 \degree\)
\(\hookrightarrow10x = 180 \degree\)
\(\hookrightarrow x = 18 \degree\)
__________________________
\( \mathrm{✌TeeNForeveR✌}\)
The Simple intrest on $765,000 invested for 3 years at 3% is?
Answers
Answer: 68850
Step-by-step explanation:
interest = 765000(3/100x3)
= 68850
if your finding total cost add 765000 + 68850 = 833850
What is the image point of (-7,0) after a translation left 4 units and up 1 unit?
Answers
Answer:
(-11, 1)
Step-by-step explanation:
x-values are horizontal and y-values are vertical
so add -4 to -7 to get -11
add 0 to 1 to get 1
new point is at (-11,1)
Consider triangle GHJ. Triangle G H J is shown. Angle G H J is a right angle. The length of the hypotenuse is 10 and the length of another side is 5. What is the length of line segment HJ?
Answers
Answer:
\(\bold{\sqrt{75}}\)
Step-by-step explanation:
Given
A \(\triangle GHJ\) in which
\(\angle GHJ = 90^\circ\)
Hypotenuse = 10
Length of another side = 5
To find:
HJ = ?
Solution:
Kindly refer to the image attached in the answer area.
We know that there are only 3 sides in a triangle.
We are given hypotenuse is 10.
i.e. GJ = 10
To find HJ, Base = ?
So, we are given the side length of GH, perpendicular i.e. 5.
Kindly refer to attached image for further details.
Let us use Pythagorean theorem here.
According to Pythagorean theorem:
\(\text{Hypotenuse}^{2} = \text{Base}^{2} + \text{Perpendicular}^{2}\\\Rightarrow GJ^{2} = GH^{2} + HJ^{2}\\\Rightarrow 10^2=5^2+HJ^2\\\Rightarrow HJ = \sqrt{100-25}\\\Rightarrow \bold{HJ = \sqrt{75}}\)
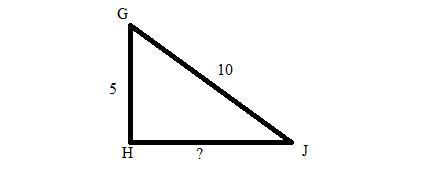
Answer:
hJ = B 5 route 3
Step-by-step explanation:
got it right on edg 2020-2021
Simplify the radical. (p.181-182, p.186)√75
( show your work)
Answers
The simplification of the given radical is \(\sqrt{7} .5p\) \(-5\sqrt{7}\) \(\sqrt{7} .5p\) \(930\sqrt{7}\)
What is a radical?A radical is a number which expresses the root of a number it is mostly square and cube root of a number. The radical can also associated with equations, expressions and inequalities.
Given, the radical,
(p.181-182, p.186) \(\sqrt{7}5\)
To simplify this radical, first we have to do the scalar multiplication,
multiply each term in the brackets by \(\sqrt{7} .5\)
we get,
(\(\sqrt{7} }.5p\) \(\sqrt{7} .5(181-182)\) \(\sqrt{7} .5p\) \(\sqrt{7} .5(186)\))
Then simplify the each term we get,
(\(\sqrt{7} .5p\) \(-5\sqrt{7}\)\(\sqrt{7} .5p\) \(930\sqrt{7}\))
Further it cannot be simplified.
Hence, the simplification of the given radical is \(\sqrt{7} .5p\) \(-5\sqrt{7}\) \(\sqrt{7} .5p\) \(930\sqrt{7}\)
Learn more about radicals here:
https://brainly.com/question/151386
#SPJ1
What is the value of y in the solution to this system of equations?
6y + x = negative59
x = negative2y + 9
Answers
Answer:
X=-8,Y=-8.5
Step-by-step explanation:
just substitute the second equation into the first one where x is and solve for y. Then playe value of y in second equation and get x.
A person 5.5ft tall casts a shadow that is 6ft long. At the same time of day a
lamppost cast an 18ft shadow. How tall is the lampost?
17.5 feet
16.5 feet
1.83 fee
15,5 feet
Answers
(5.5/6)x18
By figuring out how tall 1 foot of shadow gives, you can then multiply it by 18 to get the lamppost height.
A line has a y-intercept of -2, but has no x-intercept. Describe
this line in words, and sketch its graph.
Answers
Step-by-step explanation:
you will plot -2 on the y axis and x axis is said to be 0.
so our coordinates would be (0,-2).

Code line pre -algebra pizzazz page 183

Answers
Answer:
S. 2
X. -18
F. -20
H. 25
E. -31
B. 16
I. 17
R. 44
Step-by-step explanation:
Hope this helps.
16. Find an equation of the tangent line to the graph of the function f(x) = 4x/x^2-3 at the point (-1.2). Present the equation of the tangent line in the slope intercept form y = mx +b.
Answers
The equation of the tangent line is y = 2x + 4.
Given:
f(x) = 4x + x^2 - 3........(1).
To find the equation of tangent line at point (-1.2).
Differentiating equation w.r.t. (x) we get,
f(x) = d/dx = (4x + x^2 - 3)
f'(x) = 4 + 2x
f'(x) at (-1, 2)
f'(x) = 4 + 2×(-1)
m = 2
The slop equation.
y = mx + b.
2 = 2(-1) + b
b = 4
Therefore, the equation of the tangent line in the slope y = 2x + 4.
Learn more about tangent line here:
https://brainly.com/question/32620079
#SPJ6
The equation of the tangent line is y = 2x + 4.
Given:
f(x) = 4x + x² - 3........(1).
To find the equation of tangent line at point (-1.2).
Differentiating equation w.r.t. (x) we get,
f(x) = d/dx = (4x + x² - 3)
f'(x) = 4 + 2x
f'(x) at (-1, 2)
f'(x) = 4 + 2×(-1)
m = 2
The slope equation.
y = mx + b.
2 = 2(-1) + b
b = 4
the equation of the tangent line in the slope intercept form y = mx +b is:
y = 2x + 4.
Therefore, the equation of the tangent line in the slope y = 2x + 4.
Learn more about tangent line here:
brainly.com/question/32620079
#SPJ4