How many solutions does the following system have over the interval (-3, 1]?
f(x)= In(x+3)
g(x)= 2*6^x
Answers
The given system of equations has one solution.
How to find different solutions from intervals?To determine the number of solutions of the functions. The given system over the interval (-3, 1], we need to find the intersection points of the two functions, f(x) and g(x), within that interval.
First, let's analyze each function separately:
Function f(x) = ln(x + 3):The natural logarithm function ln(x) is only defined for positive values of x. In this case, we have ln(x + 3). To find the intersection points with the interval (-3, 1], we need to ensure that x + 3 is positive.
For x in the interval (-3, 1], we have:
-3 < x ≤ 1
Adding 3 to both sides of the inequality:
0 < x + 3 ≤ 4
Therefore, the function f(x) = ln(x + 3) is defined over the interval (0, 4].
2. Function g(x) = 2 * \(6^x\):
The exponential function \(6^x\) is always positive for any real value of x. Multiplying it by 2 won't change the fact that the function remains positive. Hence, g(x) is positive for all real values of x.
Now, let's determine the intersection points of f(x) and g(x) within the interval (-3, 1].
Since g(x) is always positive and f(x) is defined over (0, 4], the intersection points occur where f(x) = g(x) > 0.
To solve this equation, we can rewrite it as ln(x + 3) - 2 * \(6^x\) = 0.
Finding the exact solutions to this equation is not straightforward and may require numerical methods or graphing. However, it's clear that there is at least one solution within the interval (0, 4].
In conclusion, the given system has at least one solution over the interval (-3, 1].
Learn more about Solutions of the functions
brainly.com/question/13230298
#SPJ11
Related Questions
HELP?? PLEASE AND THANK YOU

Answers
Answer:
45
Step-by-step explanation:
50-5=45
after analyzing the sales data from both curbside pickup and delivery orders, a local pizza joint obtains the following 95% confidence intervals for the mean of pickup orders and delivery orders: pickup orders: between $33 and $51 per order delivery orders: between $21 and $41 per order can you conclude that an average pickup order has higher amount than an average delivery order?
Answers
Based on the information provided, we cannot conclude with certainty that the average pickup order has a higher amount than the average delivery order.
Based on the information given, we can conclude that there is a 95% chance that the true mean for pickup orders falls between $33 and $51, and the true mean for delivery orders falls between $21 and $41. However, we cannot conclude with certainty that the average pickup order has a higher amount than the average delivery order.
To determine if there is a significant difference between the means of the two groups, we need to perform a hypothesis test. We can set up our null hypothesis as "there is no significant difference between the means of the pickup and delivery orders" and our alternative hypothesis as "the average pickup order has a higher amount than the average delivery order."
We can use a two-sample t-test to test this hypothesis. Assuming equal variances, we would calculate the test statistic as
t = (xpickup - xdelivery) / (s / √n)
where xpickup and xdelivery are the sample means for pickup and delivery orders, s is the pooled standard deviation, and n is the sample size for each group.
If our calculated t-value is greater than the critical value at a chosen significance level (e.g. 0.05), we can reject the null hypothesis and conclude that there is a significant difference between the means of the two groups.
Learn more about two-sample t-test here
brainly.com/question/15870238
#SPJ4
What is a dilation of a line?
Answers
A dilation of a line is a transformation that changes the size of the line but preserves its shape.
It is a type of similarity transformation. A dilation can either be a reduction, in which the line is made smaller, or an enlargement, in which the line is made larger. In both cases, the line's shape is preserved, but the size is changed.
The center of dilation, also known as the scale factor, is a fixed point around which a dilation takes place. The scale factor is a value that represents the amount of change in size, it can be greater than 1 for an enlargement or less than 1 for a reduction.
In geometry, a dilation is represented by a multiplication of the coordinates of a point by a scale factor. For example, a dilation of a line with a scale factor of 2 will result in the line being twice as long as the original line.
In conclusion, a dilation of a line is a transformation that changes the size of the line but preserves its shape. The center of dilation or scale factor is a fixed point around which a dilation takes place and is represented by a multiplication of the coordinates of a point by a scale factor.
It can be either an enlargement or a reduction depending on the scale factor value.
Learn more about lines at
brainly.com/question/29223887
#SPJ4
The diagram shows part of a fan. OFG and OAD are sectors, centre 0, with radius 18 cm and sector angle 40° B, C, H and E lie on a circle, centre O and radius 6 cm. Calculate the shaded area.
Answers
The area of a shape is the amount of space on it:
The shaded area is 314 square centimeters
How to determine the shaded areaStart by calculating the area of sectors OFG and OAD using:
\(A = \frac{\theta}{360} * \pi r^2\)
So, we have:
\(OFG = \frac{40}{360} * \pi * 18^2\)
\(OFG = 36\pi\)
Also, we have:
\(OAD = \frac{40}{360} * \pi * 18^2\)
\(OAD = 36\pi\)
Next, calculate the area of the sectors BOE and COH
Note that the radius of these sectors is 6 cm.
So, we have:
\(COH =BOE = \frac{140}{360} * \pi * 6^2\)
\(COH = BOE = 14\pi\)
The shaded area is then calculated as:
\(Shaded = OFG + OAD + COH + BOE\)
This gives
\(Shaded =36\pi + 36\pi + 14\pi + 14\pi\)
\(Shaded =100\pi\)
The equation becomes
\(Shaded =100 * 3.14\)
\(Shaded = 314\)
Hence, the shaded area is 314 square centimeters
Read more about areas at:
https://brainly.com/question/14989383
Ronald ran 6 laps in 12 minutes. Which ratio can be used to find the number of laps that Ronald ran in 1 minute?
Answers
Answer:
6/12
Step-by-step explanation:
Got it right on test
Answer: 6 / 12
Step-by-step explanation: I took the test 2 hours ago xD
Seven less than a number is 15
Answers
Answer:
8 is 7 less than 15
What is the domain of the following ordered pairs?
(-1, 3), (0, 8), (3, 23), (-5, -17), (-3, -7)
Answers
The domain is the set of all the x-values used by those points.
{ -1, 0, 3, -5, -3 }
The order does not matter.
PLEASE HELP ASAPPP
Laura placed a bucket of water in her garden. Over the course of a week, she watched the water evaporate and recorded the volume of water left in the bucket each day.
Laura found the linear model that best fit the data was V=5.00−0.25n, where n is the number of days since she first placed the bucket and V is the volume of water, in liters, remaining in the bucket. Drag and drop the answers to complete the sentence below.
0.25 ,4.75 ,5.00
According to the model, approximately (blank) liters of water evaporated from the bucket every day, and the bucket contained (blank) liters of water when Laura first placed it in the garden.
Answers
what is 19ft in diameter
Answers
19′0″ 59.69 716.3 18.19
****The circumference of a circle is pi times its diameter
**** The diameter of a circle is the distance from one edge to the other, passing through the center. It is twice the radius
Circumference = π * Diameter
What are the answers? i’m not sure how to solve this.

Answers
Write the equation in standard form for the circle with center (2, -8) and radius 7.
Answers
The Equation of circle is (x-2)² +(y+ 8)² = 7²
The standard form of a circle with center (h, k) and radius r is given by the equation:
(x-h)² + (y-k)² = r²
In this equation, (h, k) represents the coordinates of the center of the circle, and r represents the radius of the circle.
In this case, the center of the circle is (2, -8) and the radius is 7.
Plugging these values into the equation, we have:
(x- 2)² + (y- (-8))² = 7²
Simplifying further:
(x-2)² +(y+ 8)² = 7²
So, the equation in standard form for the circle with center (2, -8) and radius 7 is:
(x-2)² +(y+ 8)² = 7²
Learn more about Equation of circle here:
https://brainly.com/question/29104982
#SPJ1
oints) Find an equation of the tangent plane to the surface z = xy-r-y at the given point (-5,3, -13).
Answers
The equation of the tangent plane is:
2x - 6y - z + 15 = 0
To find the equation of the tangent plane to the surface z = xy - x - y at the given point (-5, 3, -13), we first need to find the partial derivatives with respect to x and y, which will give us the normal vector to the plane.
∂z/∂x = y - 1
∂z/∂y = x - 1
Now, we can plug in the given point (-5, 3, -13) to find the normal vector components:
∂z/∂x(-5, 3) = 3 - 1 = 2
∂z/∂y(-5, 3) = -5 - 1 = -6
Thus, the normal vector to the plane is <2, -6, -1>.
Now we can use the point-normal form of the plane equation:
A(x - x₀) + B(y - y₀) + C(z - z₀) = 0
Plugging in the normal vector components and the given point, we get:
2(x - (-5)) - 6(y - 3) - 1(z - (-13)) = 0
Simplify the equation:
2x + 10 - 6y + 18 - z - 13 = 0
2x - 6y - z + 15 = 0
So the equation of the tangent plane is:
2x - 6y - z + 15 = 0
To learn more about tangent plane, refer below:
https://brainly.com/question/30260323
#SPJ11
Can You / Someone answer this question 4 me plzzz!!!!
What is the solution of log:
z + 12 = 9

Answers
Answer:
1/1000
Step-by-step explanation:

Determine the density of a proton. For a sphere \( V=\left(\frac{4}{3}\right) \pi r^{3} \). Express the density to two significant figures.
Answers
The density is 1.7 x 10^-27 kg/m^3.
The density of a proton can be determined by calculating its mass and volume. Given the volume of a sphere, the density of a proton can be expressed to two significant figures.
To determine the density of a proton, we need to calculate its mass and volume. The mass of a proton is approximately 1.67 x 10^-27 kilograms. The volume of a sphere is given by the formula V = (4/3)πr^3, where r is the radius. Since a proton is considered a point particle, it does not have a defined radius. Therefore, we assume the radius to be extremely small, close to zero. Substituting this value into the volume equation, we get V = (4/3)π(0)^3 = 0. However, the mass of the proton remains unchanged. Thus, the density of a proton is approximately 1.67 x 10^-27 kilograms per cubic meter. Rounded to two significant figures, the density is 1.7 x 10^-27 kg/m^3.
For more information on protons visit: brainly.in/question/16676620
#SPJ11
Please help!! Giving brainliest and extra points!! (Click on photo) (sorry if confusing!)
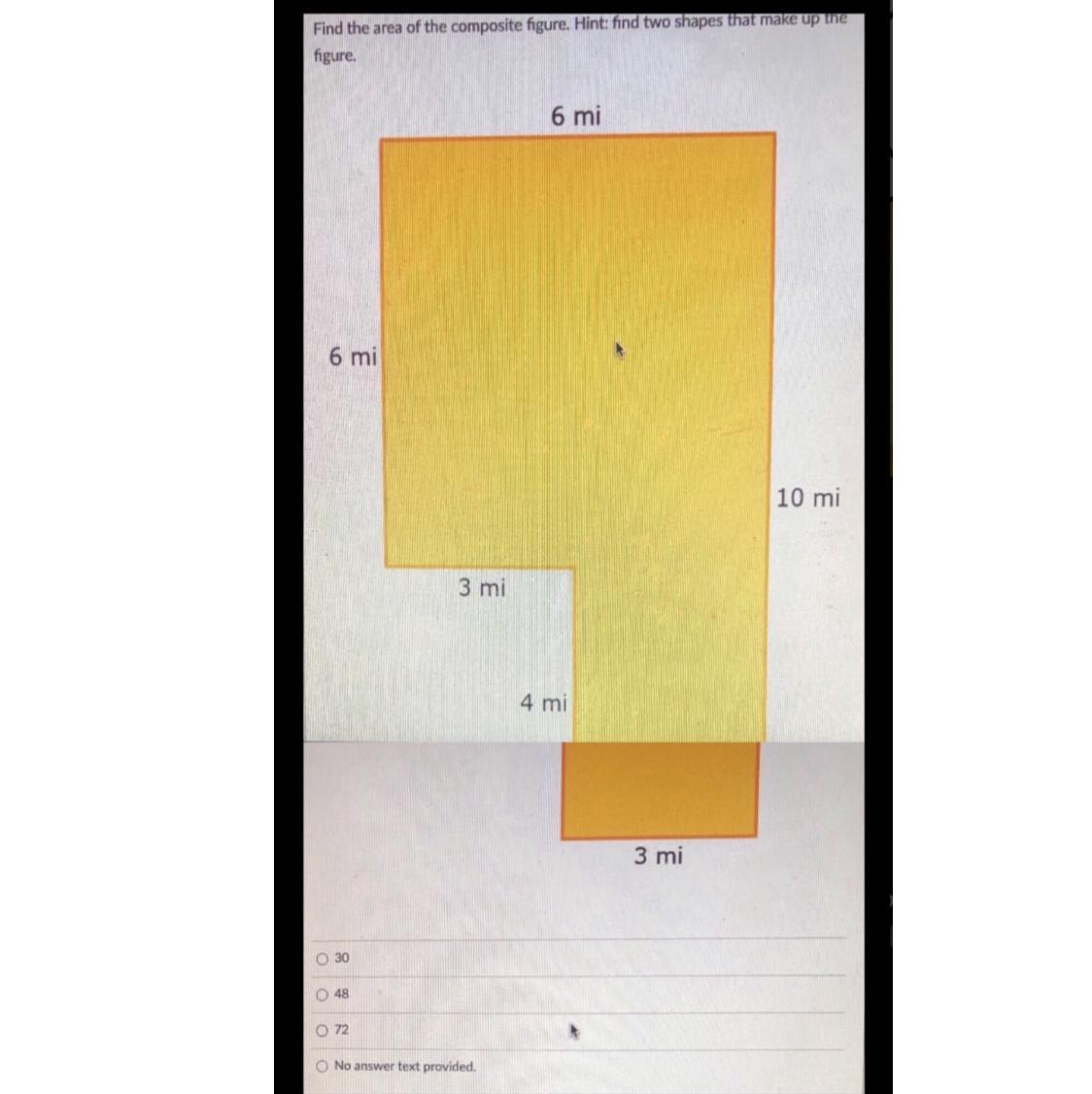
Answers
Answer:
48
Step-by-step explanation:
the top shape is 6 by 6, which is 36
the bottom shape is 3 by 4, which is 12.
if you add the two areas, 12+36, you get 48. so the area of the entire shape is 48mi
The office lunchroom is open Monday through Thursday. On Monday, 314 people ate lunch there. On Tuesday and Wednesday, 265 people ate lunch in the lunchroom. All 520 employees ate lunch there on Thursday. How many more people ate in the lunchroom on Thursday than on Monday?
Answers
Answer:
There were 206 more people on Thursday than on Monday.
Step-by-step explanation:
520 - 314 = 206
(!!!!!VERY URGENT!!!!!!) find the area of the composite figure
Answers
Each outcome on the spinner below has equal probability. If you spin the spinner three times and form a three-digit number from the three outcomes, such that the first outcome is the hundreds digit, the second outcome is the tens digit and the third outcome is the units digit, what is the probability that you will end up with a three-digit number that is divisible by $4$?
Answers
So, the probability of ending up with a three-digit number that is divisible by 4 is 1/24.
To find the probability of ending up with a three-digit number that is divisible by 4 when spinning the spinner three times, we need to consider the possible outcomes that satisfy this condition and divide it by the total number of possible outcomes. Let's analyze the given spinner and its possible outcomes:
Spinner: [1, 2, 3, 4, 5, 6]
To form a three-digit number, the hundreds digit will be determined by the first spin, the tens digit by the second spin, and the units digit by the third spin. A number is divisible by 4 if the last two digits (tens and units digits together) form a number divisible by 4. Therefore, we need to find the number of possible outcomes for the tens and units digits that satisfy this condition.
Possible outcomes for the tens digit: [2, 4, 6]
Possible outcomes for the units digit: [2, 4, 6]
Combining the possible outcomes for the tens and units digits, we have a total of 9 (3 possibilities for the tens digit multiplied by 3 possibilities for the units digit) favorable outcomes. The total number of possible outcomes for each spin is 6 (since there are 6 numbers on the spinner). Since we are spinning the spinner three times independently, the total number of possible outcomes for spinning it three times is 6^3 = 216. Therefore, the probability of ending up with a three-digit number divisible by 4 is:
Probability = favorable outcomes / total outcomes
Probability = 9 / 216
Probability = 1 / 24
To know more about probability,
https://brainly.com/question/21467996
#SPJ11
A box contains
toffee, coffee, orange, mint and hazelnut
flavour chocolates.
The ratio of toffee: coffee: orange : mint chocolates is 5:4:2:3
The
probability of picking a hazelnut chocolate i5 g
How many hazelnut chocolates are in the box?
Answers
The probability of picking a hazelnut chocolate is 1/5 and the number of hazelnut chocolates in the box is 1
How to determine the probabilityNote that the ratios = 5:4:2:3
toffee: coffee: orange: mint chocolates = 5:4:2:3:1
Total ratio = 15
Probability of picking a hazelnut chocolate = ratio of hazelnut chocolates/ total ratio
Probability of picking a hazelnut chocolate = \(\frac{1}{15}\)
The number of hazelnut chocolates in the box is gotten from the ratio which is 1
Therefore, the probability of picking a hazelnut chocolate is 1/5 and the number of hazelnut chocolates in the box is 1
Learn more about probability here:
https://brainly.com/question/24756209
#SPJ1
After multiplying, a calculator screen displays the answer shown below. How would you write this number in standard form?
Answers
The distance it takes a truck to stop can be modeled by the function Image description d = stopping distance in feet v = initial velocity in miles per hour f = a constant related to friction When the truck's initial velocity on dry pavement is 40 mph, its stopping distance is 138 ft. Determine the value of f, rounded to the nearest hundredth.
Answers
Answer: 0.39
Step-by-step explanation:

We are required to determine the the value of f, rounded to the nearest hundredth
The value of f, rounded to the nearest hundredth is 0.39
Given function:
\(d(v) = \frac{2.15 {v}^{2} }{64.4f} \)
Where,
d = stopping distance in feet
v = initial velocity in miles per hour
f = a constant related to friction
When
v = 40 mph
d = 138 ft
f = ?
\(d(v) = \frac{2.15 {v}^{2} }{64.4f} \)
\(138= \frac{2.15 {(40)}^{2} }{64.4f} \)
138(64.4f) = 2.15(1600)
8,887.2f = 3440
f = 3440 / 8,887.2
f = 0.3870735439733
Approximately to the nearest hundredth f = 0.39
Therefore, the value of f, rounded to the nearest hundredth is 0.39
Read more:
https://brainly.com/question/10307723

Which equation describes the line with a slope of -3 that contains the point (2,4)?

Answers
Answer: y = 2x - 11
Step-by-step explanation:
A linear equation has the following form.
y = a . x + b
where,
y: independent variable
a: slope
x: independent variable
b: y-intercept
The slope is 2, so a is 2. The ordered pair (4, -3) means that when x takes the value 4, y takes the value -3. We can replace these values in the general equation to find the y-intercept.
y = a . x + b
-3 = 2 . 4 + b
b = -11
The linear equation is
y = 2x - 11
Answer:
C. is the correct option
Step-by-step explanation:
When we find the equation using the point and slope formula, we get y=-3x+10
As you can see, that doesn't match any of the answers, since it is in the point-slope formula.
We can start solving all the equations to rule out the correct one, but to save yourself from reading all of this, I'll just do there C.
For this equation, we will distribute the 3, and then add 4 to both sides.
y-4=-3(x-2) ---> y-4=-3x+6 ---> y-4(+4)=-3x+6(+4) ---> y=-3x+10
This leads back to the original equation so we know it is correct.
Theorem: The average of any two real numbers is less than or equal to at least one of the two numbers. A proof by contradiction of the theorem starts by assuming which fact? Group of answer choices There exists two real numbers, x and y, such that (x+y)/2\gtx or (x+y)/2\gty. For every two real numbers, x and y, (x+y)/2\gtx or (x+y)/2\gty. There exists two real numbers, x and y, such that (x+y)/2\gtx and (x+y)/2\gty. For every two real numbers, x and y, (x+y)/2≤x or (x+y)/2≤y.
Answers
To prove the theorem by contradiction, we start by assuming the fact that there exist two real numbers, x, and y, such that (x+y)/2 is greater than both x and y individually, i.e., (x+y)/2 > x or (x+y)/2 > y. So, the first option is correct.
The proof by contradiction of the theorem starts by assuming that: "There exists two real numbers, x, and y, such that (x+y)/2 > x and (x+y)/2 > y." The proof by contradiction of the theorem is as follows:
Suppose, for the sake of contradiction, that (x+y)/2 > x and (x+y)/2 > y for all real numbers x and y.
This implies that (x+y) > 2x and (x+y) > 2y.
Adding these inequalities gives 2x + 2y < 2(x + y), or equivalently, x + y < x + y, which is impossible, since x + y = x + y for all real numbers x and y. Therefore, our initial assumption that (x+y)/2 > x and (x+y)/2 > y for all real numbers x and y must be false.
So there must be at least one pair of real numbers x and y such that (x+y)/2 ≤ x or (x+y)/2 ≤ y, which proves the theorem.
Hence, the option that is correct is - "There exists two real numbers, x, and y, such that (x+y)/2 > x or (x+y)/2 > y."
"There exists two real numbers, x, and y, such that (x+y)/2 > x or (x+y)/2 > y." This assumption is made to establish the contradiction that leads to the proof of the theorem.
The concept being used in the proof by contradiction is the assumption that contradicts the theorem in order to demonstrate that the theorem must be true.
In this case, the theorem states that the average of any two real numbers is less than or equal to at least one of the two numbers. The proof by contradiction aims to show that this statement is always true by assuming the opposite and reaching a contradiction.
The assumption made is that there exist two real numbers, x, and y, such that (x+y)/2 > x or (x+y)/2 > y. This assumption implies that the average of x and y is greater than one or both of the numbers individually.
To prove the theorem by contradiction, the assumption is examined and shown to lead to a contradiction with the properties of real numbers. This contradiction arises when it is shown that the assumption cannot hold true for all possible choices of x and y.
By reaching a contradiction, it demonstrates that the initial assumption was false, and therefore the opposite must be true. Hence, the theorem is proven to be valid: the average of any two real numbers is indeed less than or equal to at least one of the two numbers.
Learn more about proof by contradiction at:
brainly.com/question/30459584
#SPJ11
24. 075 21.048 24.008 21 .605 how do i answer this from greatest to least
Answers
Answer:
24.075, 24.008, 21.605, 21.048
The price of a bus ticket to Saskatoon is $180. This bus has 56 seats. The bus company is considering dropping the bus fare as part of a promotion to increase the ridership on that route. Lately, the busses have only been at half capapcity. The bus company's research shows that for every $5 decrease they will gain 2 more riders.
a) define variables and set up an equation to represent this scenario
b) What is the maximum revenue the bus company can earn and what will be the cost of a ticket when the revenue is at a maximum
Answers
If the price of one ticket of bus is $180 and the bus has 56 seats then the maximum revenue that it can earn is $5107.6
Given that the price of a bus ticket to Saskatoon is $180 and the bus has 56 seats.
We are required to find the maximum revenue that the bus company can earn.
Suppose x represents the number of seats, y represents the total amount.
Price=$156
Seats=56
When the bus is of half capacity the bus seats will be 28.
As price decreases th rider gains 2 more.
Revenue equation.
y=(156.5x)(28+2x)-------------1
Expanding the equation.
y=4368-140x+312-10\(x^{2}\)
Differentiating with respect to x.
dy/dx=0-140+312-20x
=172-20x
Put dy/dx=0
172-20x=0
x=8.6
Substitute the value of variable x in the equation 1.
y=(156-5x)(28+2x)
=$5107.6
Hence the maximum revenue that the bus company can earn is $5107.6.
Learn more about differentiation at https://brainly.com/question/954654
#SPJ1
How do you know if a graph is wider or narrower than the parent function?
Answers
The parabola narrows as the quadratic coefficient increases. The parabola's width increases as the quadratic coefficient decreases.
Define the condition for wider graph of the parent function?The graphs' width and whether or not they slant upward or downward depend on the quadratic term's coefficient, a for the parent function.
The parabola ends point up when the quadratic coefficient is positive.The parabola's ends point down when the quadratic coefficient is negative.The parabola narrows as the quadratic coefficient increases.The parabola's width increases as the quadratic coefficient decreases.The axis of symmetry is moved away from the y-axis by the linear-term coefficient b. The quadratic coefficient's sign and the linear coefficient's sign both affect the shift's direction.The y-intercept is impacted by the constant term c. The intercept point just on y-axis increases higher the higher the number is.To know more about the parent function, here
https://brainly.com/question/17079244
#SPJ4
Gina Needs To Pack 130 Pens, 50 Pencils And 20 Erasers Into Identical Gift Bags So That Each Item Is Equally Distributed Among The Gift Bags. (I) Find The Largest Number Of Gift Bags That Can Be Packed. (Ii) Find The Number Of Each Item In A Gift Bag.
Answers
Answer:
Step-by-step explanation:
I think the best way is to split up the erasers before you do anything. That would mean there were 20 gift bags in all
If you did that, then each gift bag would contain 2 pencils with 10 left over.
Further 130 pens would divide up into 6 pens in each gift bag with 10 pens left over.
The trinomial x² - 14x + 49 can be expressed as
(1) (x-7)²
(2) (x + 7)²
(3) (x-7)(x + 7)
(4)) (x-7)(x + 2)
Answers
Answer:
(1)
Step-by-step explanation:
This is because (x-7)²=(x-7)(x-7), which when expanded using the FOIL method, is equal to x²-7x-7x+49=x²-14x+49.
x + 3y = -3 solve for Y (ex. y= 3 + 5x
Answers
Answer:
y = -1/3x - 1
Step-by-step explanation:
Let's solve for y.
Step 1: Add -x to both sides.
x+3y+−x=−3+−x
3y=−x−3
Step 2: Divide both sides by 3.
y=-1/3x-1
--
\(\frac{-1}{3} x-1\)
If you answer all 5 will give branliest ty for whoever helps

Answers
2)b,h and c,e
3)a,g and d,f
4)c,h and b,e
5)d,b and h,f