H(x)= 3x^4+2x—5/x+9x^3-7, is it a polynomial? If so write in standard form, degree, type, and leading coefficient.
Answers
The function H(x) = 3x⁴ + 2x — 5/x + 9x³ - 7 is not a polynomial function
What is a polynomial function?A polynomial function is a function in an equation, such as the quadratic equation, cubic equation, etc., that only uses non-negative integer powers or only positive integer exponents of a variable.
A polynomial with an exponent of 1 is, for instance, 2x+5.
The given polynomial in standard form is written as
H(x) = 3x⁴ + 2x — 5/x + 9x³ - 7
H(x) = 3x⁴ + 9x³ + 2x - 7 - 5x⁻¹
this shows that on of the term has a negative exponent 5x⁻¹ and hence not a polynomial
the leading coefficient is 3
Learn more about polynomial at:
https://brainly.com/question/2833285
#SPJ1
Related Questions
Answer fast pls
Solve for x
(x/x-2)+1/5=(2/x-2)
8
2
6
4
Answers
Answer: 4
Step-by-step explanation: To solve the equation (x/(x-2)) + (1/5) = (2/(x-2)), we can follow these steps:
Step 1: Find a common denominator for the fractions on the left-hand side of the equation. The common denominator will be (5(x-2)).
Step 2: Rewrite the equation using the common denominator:
[(5(x)/(x-2)) + (1(x-2))/(5(x-2))] = (2/(x-2))
Step 3: Simplify the equation:
(5x + (x - 2))/(5(x-2)) = (2/(x-2))
Step 4: Combine like terms:
(6x - 2)/(5(x-2)) = (2/(x-2))
Step 5: Cross-multiply to eliminate the denominators:
(6x - 2)(x-2) = 2 * 5(x-2)
Step 6: Expand and simplify both sides of the equation:
6x^2 - 20x + 4 = 10x - 20
Step 7: Rearrange the equation to one side:
6x^2 - 30x + 24 = 0
Step 8: Divide the equation by 6 to simplify:
x^2 - 5x + 4 = 0
Step 9: Factor the quadratic equation:
(x - 4)(x - 1) = 0
Step 10: Solve for x:
x - 4 = 0 or x - 1 = 0
x = 4 or x = 1
Therefore, the solutions for x are 4 and 1.
3: 5 and 2:10 is are equivalent . explain
Answers
The ratios are not equivalent.
Jamie is 5 years older than her sister amy. If the sum of their ages is 19. how old is Jamie?
Answers
Considering the age of Amy and sum of their ages, Jamie is 12 years old.
Let the age of Amy be x years. Thus, the age of Jamie be (x + 5) years. Forming equation as per the age -
x + x + 5 = 19
Performing addition on Left Hand Side of the equation
2x + 5 = 19
Shifting 5 to Right Hand Side of the equation
2x = 19 - 5
Performing subtraction on Right Hand Side of the equation
2x = 14
Shifting 2 to Right Hand Side of the equation
x = 14 ÷ 2
Performing division to Right Hand Side of the equation
x = 7
The age of Amy = 7 years
The age of Jamie = 7 + 5
Performing addition
The age of Jamie = 12 years
Thus, the age of Jamie is 12 years old.
Learn more about expression -
https://brainly.com/question/723406
#SPJ1
solve the following system of equations using substitution
x = 4
2x + 4y = 36
Answers
2*4 +4y =36
8+4y =36
4y =36-8
4y=28
y= 28/4
y=7
Step-by-step explanation:
2x + 4y = 36
2 × 4 + 4y = 36
8 + 4y = 36
4y = 36 - 8
4y = 28
y = 28 ÷ 4
y = 7
The density, d, of an object can be found by using the formula d=\(\frac{m}{v}\), where m is the mass of the object and v is its volume. What is the density of an object that has a mass of 73,430 kilograms and a volume of 7 \(m^{3}\)
Answers
The density of an object is 10490kg/m^3.
How to find the density?Density is like rate. It tells you how much of a thing is available for each unit other thing which contains the first thing.
Density = (Total amount available)/(total space which contains that amount)
Given;
The mass of object= 73,430 kilograms
The volume of object= 7m^3
Now
D=mass/volume
D=73430/7
D=10490
Therefore, the density will be 10490kg/m^3.
Learn more about density here:
https://brainly.com/question/12630910
#SPJ1
Alex knits hats and scarves to sell at a craft market. He can make at most 20 hats and 30 scarves, but no more than 40 items altogether, in time for the market.
Write and graph a system of inequalities that shows the possible numbers of hats and scarves Alex can bring to the craft market if he wants to bring at least 25 items. Identify three (3) possible combinations, and say which he should
choose.
Answers
The three (3) possible combinations are
hats = 10, scarves = 30hats = 10, scarves = 20hats = 20, scarves = 20Alex should 20 hats and 20 scarves
How to find the possible combinations Alex can bring to the marketLet the number of scarves be x and y be the number of hats
He can make at most 20 hats and 30 scarves, but no more than 40 items altogether
x ≤ 20
y ≤ 30
x + y ≤ 40 (in time of market)
x + y ≥ 25
The possible combinations are
1 ⇒ x = 10, y = 302 ⇒ x = 10, y = 203 ⇒ x = 20, y = 20He should choose the third option x = 20, y = 20 this allows him to take more products to the show
Learn more about inequality graph at:
https://brainly.com/question/11234618
#SPJ1

Subtract (6x² + 8x - 5) from (7x? + 8x - 4)
Answers
Answer:
−6x^2+7x+1
Step-by-step explanation:
1)(7x+8x-4)=15x−4
2)15x-4-(6x^2+8x-5)=−6x2+7x+1
. the function f is linear, f(1) = −4, and f intersects the x-axis at an angle of 150° (measured counterclockwise from the x-axis, as usual). find a formula for f and leave your answer in exact form
Answers
Given that the function f is linear, f(1) = −4, and f intersects the x-axis at an angle of 150° (measured counterclockwise from the x-axis, as usual). To find a formula for f and leave the answer in exact form, let's proceed as follows: Let a be the slope of the linear function, f(x) = ax + b.
Given that the function f is linear, f(1) = −4, and f intersects the x-axis at an angle of 150° (measured counterclockwise from the x-axis, as usual). To find a formula for f and leave the answer in exact form, let's proceed as follows: Let a be the slope of the linear function, f(x) = ax + b.
At point (1, -4), we have-4 = a(1) + b ...(1)
Also, given that f intersects the x-axis at an angle of 150° (measured counterclockwise from the x-axis), we can use the angle θ that f makes with the positive x-axis to find the slope as follows: tan θ = a ...(2)
Since the angle with x-axis is 150°, the angle made with the positive x-axis is 30°.
Hence, tan 30° = 1 / √3
Therefore, a = 1 / √3. Hence, from equation (1), -4 = (1 / √3) + b ⇒ b = -4 - (1 / √3)
Thus, the equation of the linear function f is
f(x) = (1 / √3)x - (4 + 1 / √3).
Therefore, the formula for f is given by f(x) = (1 / √3)x - (4 + 1 / √3).
To know more about x-axis visit:
https://brainly.com/question/1442188
#SPJ11
Which statement best describes the composition of most foods? They contain mixtures of the three energy nutrients, although only one or two may predominate. They contain only two of the three energy nutrients, and those two are contained in equal amounts. They contain equal amounts of the three energy nutrients, Most contain only one of the three energy nutrients, although a few contain all of them
Answers
The statement that best describes the composition of most foods is: "They contain mixtures of the three energy nutrients, although only one or two may predominate."
Most foods contain mixtures of the three energy nutrients, namely carbohydrates, proteins, and fats. However, the relative proportions of these nutrients can vary significantly from one food to another. In some foods, one or two of these nutrients may predominate, while others may contain relatively equal amounts of all three.
Carbohydrates are a primary source of energy for the body and can be found in various forms such as sugars, starches, and fibers. Foods like grains (e.g., rice, wheat, oats), fruits, vegetables, and legumes tend to be rich in carbohydrates. However, the specific types and amounts of carbohydrates can vary widely.
Proteins are crucial for building and repairing tissues, as well as for various metabolic functions. Foods like meat, poultry, fish, eggs, dairy products, legumes, nuts, and seeds are excellent sources of protein. Again, the protein content in different foods can vary.
Fats, also known as lipids, are an important energy source and provide essential fatty acids. Foods such as oils, butter, avocados, nuts, and fatty meats are high in fats. Like carbohydrates and proteins, the fat content in foods can differ significantly.
It's worth noting that some foods may predominantly consist of one specific nutrient. For example, pure sugar is almost entirely composed of carbohydrates, while pure oil is almost entirely composed of fats. However, most whole foods, such as fruits, vegetables, grains, meats, and dairy products, contain a mixture of these energy nutrients.
Furthermore, a balanced diet typically includes a combination of these nutrients in appropriate proportions. A varied diet that incorporates a range of foods from different food groups helps ensure an adequate intake of carbohydrates, proteins, and fats, along with other essential nutrients required for optimal health.
To know more about nutrients, refer here:
https://brainly.com/question/32353931
#SPJ4
Find EF given E(-7, -2) and F(11, 3). Round your answer to the nearest thousandth (3 decimal places).
Answers
Answer:
18.682
Step-by-step explanation:
Given that :
E = (-7, - 2) ; x1 = - 7 ; y1 = - 2
F = (11, 3) ; x2 = 11 ; y2 = 3
EF = √((x2 - x1)² + (y2 - y1)²)
EF = √((11 - -7)² + (3 - -2)²)
EF = √((11 + 7)² + (3 + 2)²)
EF = √(18² + 5²)
EF = √324 + 25
EF = √349
EF = 18.6815
EF = 18.682 units (3 decimal places )
Please help me NO LINKS
✌︎('ω'✌︎ )

Answers
Answer:
Use the Substitution method
The answer to the problem is x = 10, y = -1
Find the area of the trapezoid

Answers
Answer:
Area:1298
Step-by-step explanation:
Area of a trapezoid is found with the formula, A=(a+b)/2 x h. So, for this instance to find the area the formula would be, (62+56)/2 x 22.
Hope I could help!:)
Find an equation for the line tangent to the graph of the given function at the indicated point. 8 3) f(x): () = at at (4,2) X 1 4) f(x)=x2-x at (4, 12)
Answers
(a) tangent line to the graph of f(x) = x^3 at the point (4,2).
(b) equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12).
(a) To find the equation of the tangent line to the graph of f(x) = x^3 at the point (4,2), we need to find the slope of the tangent line at that point. We can do this by taking the derivative of f(x) with respect to x and evaluating it at x = 4. The derivative of f(x) = x^3 is f'(x) = 3x^2. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Once we have the slope, we can use the point-slope form of a linear equation to write the equation of the tangent line.
(b) Similarly, to find the equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12), we differentiate f(x) to find the derivative f'(x). The derivative of f(x) = x^2 - x is f'(x) = 2x - 1. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Using the point-slope form, we can write the equation of the tangent line.
In both cases, the equations of the tangent lines will be in the form y = mx + b, where m is the slope and b is the y-intercept.
Learn more about line tangent: brainly.com/question/30162650
#SPJ11
birthdays of 10 members of a club are assumed to be independently and uniformly distributed over the twelve months of the year. let z be the number of months in which at least one member has a birthday. find e(z).
Answers
E(z),the expected value of z in which at least one member has a birthday in 12 months is (11/12)^10
Define the random variable Zi’s as
\(Z_{i}\)= 1 : if no member of the club has a birthday in the month
= 0: otherwise for, i =1,2, ......,12 .
Now, we have,
= P (\(Z_{i}\) =1) .
=p( no member of the club has a birthday in month i).
= p, say.
Now, there are a total of 10 members in the club and their birthdays are assumed to be independently and uniformly distributed over the 12 months of the year. So, there are 12 possible choices of months for each of the 10 members for their birthday. Thus, the total no. of exhaustive mutually exclusive and equally likely no. of ways of birthdays 12^10.
Again, if no member of the club has a birthday in month 'i'; then, all of their birthdays should be on the remaining (12 - 1) = 11 months of the year. So, there are possible choices of birthday months for each of the 10 members of the club. So, the no. of cases for the event (Zi=1) is 11^10.
So, p(\(Z_{i}\)=1) = Favorable no. of cases for Zi=1) / Total no. of all possible cases
= 11^10 / 12^10
By the classical definition of probability.
= (11/12)^10
p(\(Z_{i}\) = 1) = (11/12)^10
E(Zi).= (11/12)^10
Learn more about expected value Visit : brainly.com/question/17279079
#SPJ4
PLEASE HELP. 23 POINTS AND BRAINLIST.
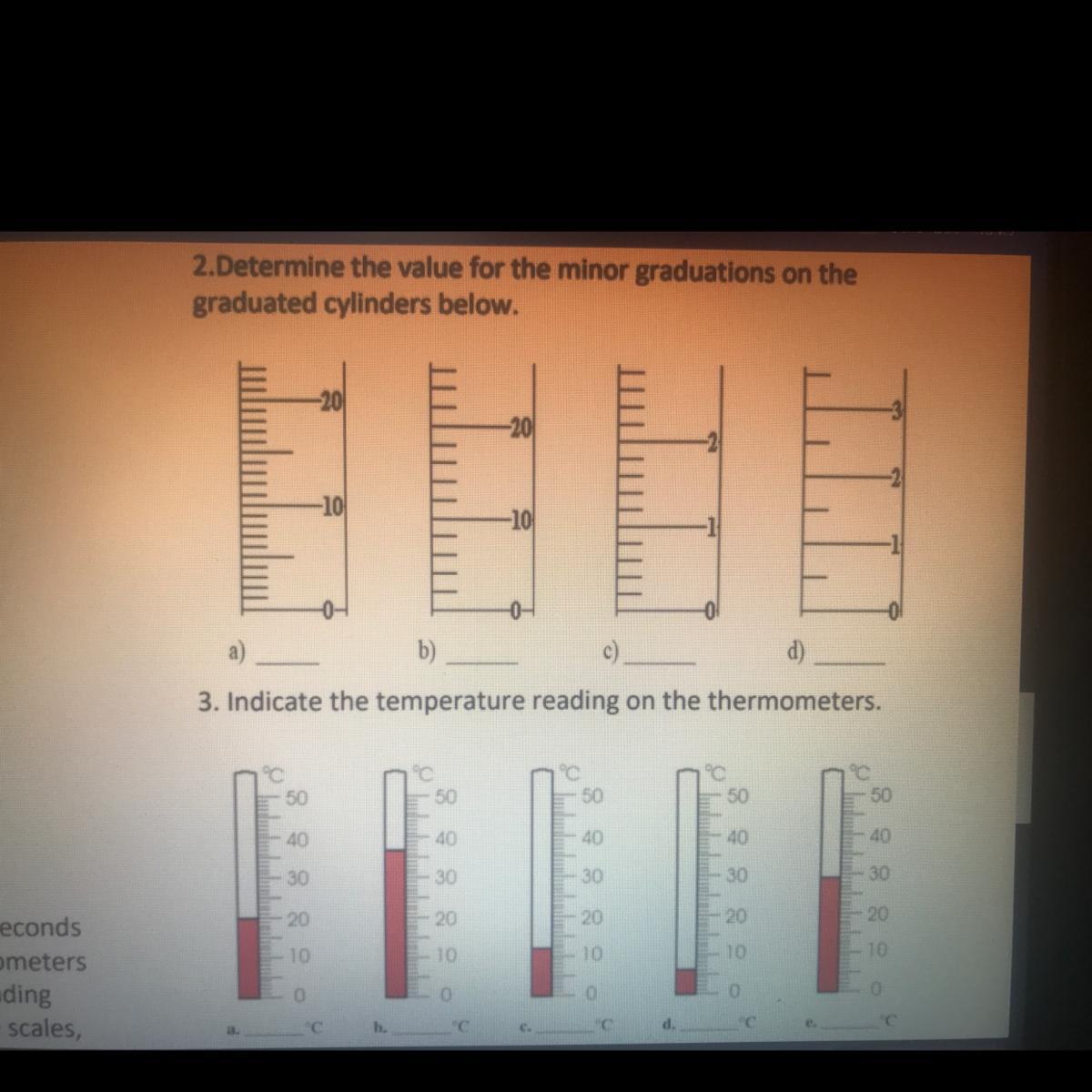
Answers
Answer:
Step-by-step explanation:

A garden is shaped in the form of a regular heptagon (seven-sided), MNSRQPO. A circle with center T and radius 25m circumscribes the heptagon as shown in the diagram. The area of ΔMSQ is left for a children's playground, and the rest of the garden is planted with flowers. Find the area of the garden planted with flowers.

Answers
The relationship between the sides MN, MS, and MQ in the given regular heptagon is \(\dfrac{1}{MN} = \dfrac{1}{MS} + \dfrac{1}{MQ}\)
The area to be planted with flowers is approximately 923.558 m²
The reason the above value is correct is as follows;
The known parameters of the garden are;
The radius of the circle that circumscribes the heptagon, r = 25 m
The area left for the children playground = ΔMSQ
Required;
The area of the garden planted with flowers
Solution:
The area of an heptagon, is;
\(A = \dfrac{7}{4} \cdot a^2 \cdot cot \left (\dfrac{180 ^{\circ}}{7} \right )\)
The interior angle of an heptagon = 128.571°
The length of a side, S, is given as follows;
\(\dfrac{s}{sin(180 - 128.571)} = \dfrac{25}{sin \left(\dfrac{128.571}{2} \right)}\)
\(s = \dfrac{25}{sin \left(\dfrac{128.571}{2} \right)} \times sin(180 - 128.571) \approx 21.69\)
\(The \ apothem \ a = 25 \times sin \left ( \dfrac{128.571}{2} \right) \approx 22.52\)
The area of the heptagon MNSRQPO is therefore;
\(A = \dfrac{7}{4} \times 22.52^2 \times cot \left (\dfrac{180 ^{\circ}}{7} \right ) \approx 1,842.94\)
\(MS = \sqrt{(21.69^2 + 21.69^2 - 2 \times 21.69 \times21.69\times cos(128.571^{\circ})) \approx 43.08\)
By sine rule, we have
\(\dfrac{21.69}{sin(\angle NSM)} = \dfrac{43.08}{sin(128.571 ^{\circ})}\)
\(sin(\angle NSM) =\dfrac{21.69}{43.08} \times sin(128.571 ^{\circ})\)
\(\angle NSM = arcsin \left(\dfrac{21.69}{43.08} \times sin(128.571 ^{\circ}) \right) \approx 23.18^{\circ}\)
∠MSQ = 128.571 - 2*23.18 = 82.211
The area of triangle, MSQ, is given as follows;
\(Area \ of \Delta MSQ = \dfrac{1}{2} \times 43.08^2 \times sin(82.211^{\circ}) \approx 919.382^{\circ}\)
The area of the of the garden plated with flowers, \(A_{req}\), is given as follows;
\(A_{req}\) = Area of heptagon MNSRQPO - Area of triangle ΔMSQ
Therefore;
\(A_{req}\)= 1,842.94 - 919.382 ≈ 923.558
The area of the of the garden plated with flowers, \(A_{req}\) ≈ 923.558 m²
Learn more about figures circumscribed by a circle here:
https://brainly.com/question/16478185
helpppp asap please!!!!

Answers
Answer:
Angle at x is 75°
Step-by-step explanation:
Data :
Angle at A = 65°
Angle at B = 40°
According to the porperty of triangle we know that total interior angle a triangle has is 180° irrespect of type or size
A + B + C = 180
65 + 40 + C = 180
C = 180 - 65 - 40 = 75°
Mark brainliest if you understand
please help me
thanks

Answers
..no lo sé, pero como necesito puntos, ¿sí?
I don't understand how to solve this. How do I find out the "Solution Region"

Answers
The graph of the solution region for the system of inequalities can be seen on the image at the end.
How to find the solution region?The solution region refers to the region where all the points are solutions of the system of inequalities.
The system of inequalities here is:
y < -x - 2
y < (1/4)x + 2
Notice that the two lines are already graphed, and "y" is smaller than the lines, so we need to shade all the region below the two lines.
The intersection of the shaded regions will be the region of solutions, the graph can be seen in the image below.
Learn more about systems of inequalities:
https://brainly.com/question/9774970
#SPJ1

Judy bought 2 1/3 pounds of apples and 2 1/6 pounds of bananas. What was the total weight of the fruit she purchased?
Answers
Answer:
4 1/2
Step-by-step explanation:
2 1/3 pounds and 2 1/6 pounds
convert the 1/3 pounds into x/6 by multiplying both numerator and denominator by 2 which equals 2/6
Then add 2+2 which gives 4 and the 1/6 and 2/6 which is equal to 3/6 which simplifies into 1/2.
4 1/2
1) The diameter of a pizza is 14 inches. What is the circumference of the
pizza? Use 22/7 for pi.
Answers
12.23 i dont know what the awnswer is bu hahahah
PLEASE HELP! Geometry property question.
Justify each of the following statements using a property of equality, property of congruence, definition, or postulate.
Please match all of them!

Answers
Answer:
Step-by-step explanation:
1. If PQ = PQ then PQ ≅ PQ
Reflexive Property of congruence
2. If K is between J and L, then JK + KL = JL
Segment addition property
3. EF ≅ EF
Definition of congruence
4. If RS = TU, then RS + XY = TU + XY
Addition property of equality
5. If AB = DE, then DE = AB
Symmetric property of equality
if a typical somatic cell (somatic cell = typical body cell) has 64 chromosomes, how many chromosomes are expected in each gamete of that organism?
Answers
If a typical somatic cell has 64 chromosomes, each gamete of that organism is expected to have 32 chromosomes.
In sexually reproducing organisms, somatic cells are the cells that make up the body and contain a full set of chromosomes, which includes both sets of homologous chromosomes. Gametes, on the other hand, are the reproductive cells (sperm and egg) that contain half the number of chromosomes as somatic cells.
During the process of gamete formation, called meiosis, the number of chromosomes is halved. This reduction occurs in two stages: meiosis I and meiosis II. In meiosis I, the homologous chromosomes pair up and undergo crossing over, resulting in the shuffling of genetic material. Then, the homologous chromosomes separate, reducing the chromosome number by half. In meiosis II, similar to mitosis, the sister chromatids of each chromosome separate, resulting in the formation of four haploid daughter cells, which are the gametes.
Since a typical somatic cell has 64 chromosomes, the gametes produced through meiosis will have half that number, which is 32 chromosomes. These gametes, with 32 chromosomes, will combine during fertilization to restore the full set of chromosomes in the offspring, creating a diploid zygote with 64 chromosomes.
Learn more about zygote here :
brainly.com/question/29769026
#SPJ11
2 ptsQuestion 1Given: BACOAD ONLA ZOProve: ABAD ACON1. BACO, ADONZA 201. (Select)2. ABAD ACON2Select)(Picture will be provided.)
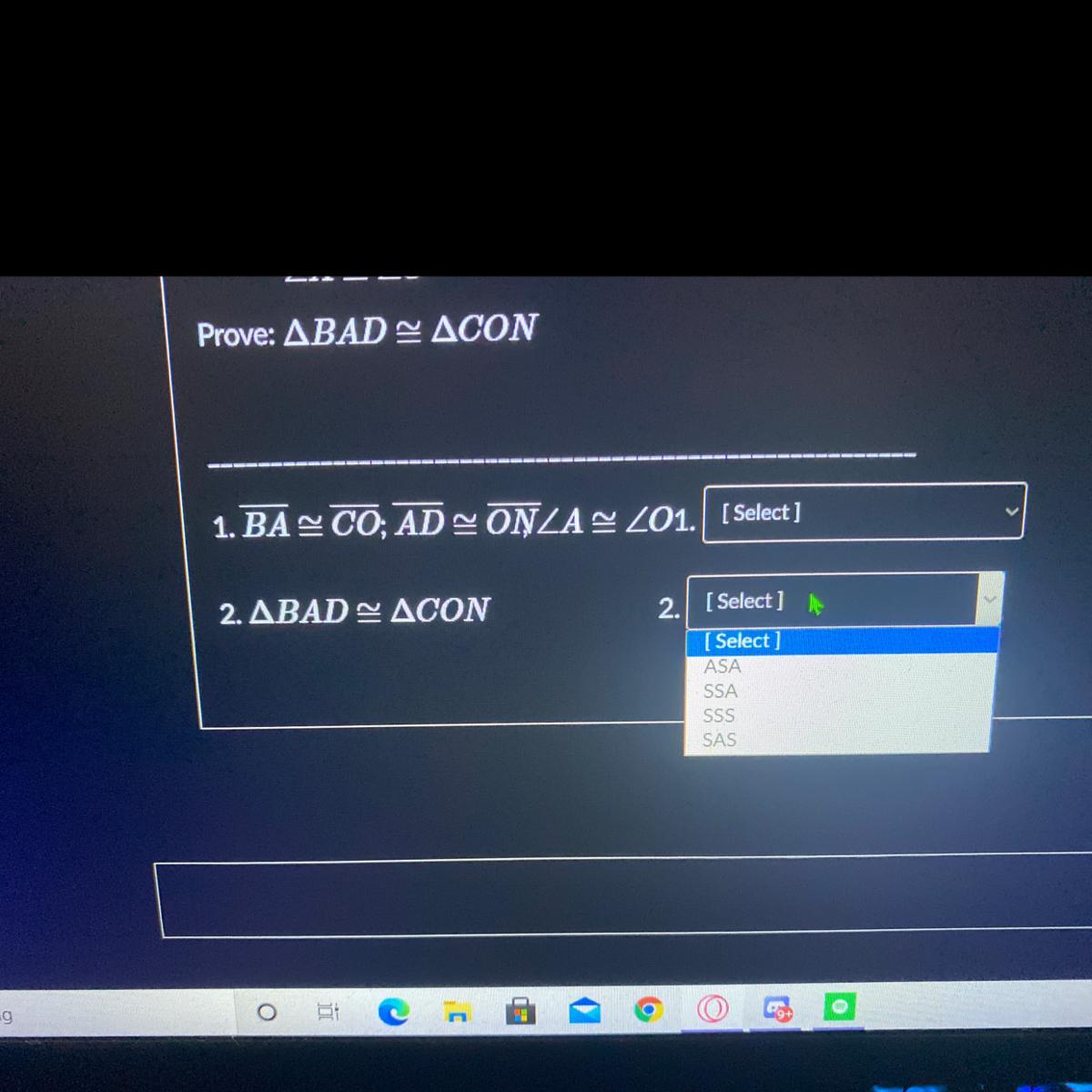
Answers
We are given the following picture
We are given the following statements
- Line BA is congruent to line OC
- Line ON is congruent to line DA
- Angle A is congruent to angle O
If we highlight the congruencies we get
where the matching colors indicate congruency. As we can see, we have a pair of sides that are congruent and the included angle are also congruent. This is the condition for the SAS theorem to apply. Hence both triangles are congruent by the SAS theorem


if using the method of completing the square to solve the quadratic equation x^2+17x+3=0x 2 +17x+3=0, which number would have to be added to "complete the square"?
Answers
Answer:
Step-by-step explanation:
answer:289/4
x² + 17x + 12 = 0
x² + 17x = -12
Take half of the second coefficient, square it, then add the result to both sides.
(17/2)² = 289/4
x² + 17x + 289/4 = -12 + 289/4
(x + 17/2)² = 241/4
Answer:
i think it might be 72.5
also theres an app called air math it could possibly help with questions you have
Step-by-step explanation:
.
the lady tasting tea. this is one of the most famous experiments in the founding history of statistics. in his 1935 book the design of experiments (1935), sir ronald a. fisher writes, a lady declares that by tasting a cup of tea made with milk she can discriminate whether the milk or the tea infusion was first added to the cup. we will consider the problem of designing an experiment by means of which this assertion can be tested . . . our experiment consists in mixing eight cups of tea, four in one way and four in the other, and presenting them to the subject for judgment in a random order. . . . her task is to divide the 8 cups into two sets of 4, agreeing, if possible, with the treatments received. consider such an experiment. four cups are poured milk first and four cups are poured tea first and presented to a friend for tasting. let x be the number of milk-first cups that your friend correctly identifies as milk-first. (a) identify the distribution of x. (b) find p(x
Answers
P(X = k) = (1 - p)^4 for k = 0
P(X = k) = 4p(1 - p)^3 for k = 1
P(X = k) = 6p^2(1 - p)^2 for k = 2
P(X = k) = 4p^3(1 - p) for k = 3
P(X = k) = p^4 for k = 4
Note that these probabilities add up to 1, as they should for any probability distribution.
(a) The distribution of X can be modeled as a binomial distribution with parameters n = 4 and p, where p is the probability that the friend correctly identifies a milk-first cup as milk-first. Each cup that the friend tastes can either be identified correctly (success) or incorrectly (failure), and there are 4 cups that were poured milk-first in the experiment.
(b) To find the probability mass function (PMF) of X, we need to find the probability of each possible value of X. Since X is a binomial random variable, the PMF of X is given by:
P(X = k) = (n choose k) * p^k * (1 - p)^(n - k)
where (n choose k) is the binomial coefficient, given by:
(n choose k) = n! / (k! * (n - k)!)
where n! denotes the factorial of n.
In this case, n = 4 and there are 4 cups that were poured milk-first, so we have:
P(X = 0) = (4 choose 0) * p^0 * (1 - p)^4 = (1 - p)^4
P(X = 1) = (4 choose 1) * p^1 * (1 - p)^3 = 4p(1 - p)^3
P(X = 2) = (4 choose 2) * p^2 * (1 - p)^2 = 6p^2(1 - p)^2
P(X = 3) = (4 choose 3) * p^3 * (1 - p)^1 = 4p^3(1 - p)
P(X = 4) = (4 choose 4) * p^4 * (1 - p)^0 = p^4
Since X can only take on values between 0 and 4, the PMF of X is given by:
P(X = k) = (1 - p)^4 for k = 0
P(X = k) = 4p(1 - p)^3 for k = 1
P(X = k) = 6p^2(1 - p)^2 for k = 2
P(X = k) = 4p^3(1 - p) for k = 3
P(X = k) = p^4 for k = 4
Note that these probabilities add up to 1, as they should for any probability distribution.
Visit to know more about Probability:-
brainly.com/question/13604758
#SPJ11
Explain the basic electricity terminologies and units, conductor, electrical circuit, current/ ampere. voltage, resistance and watts
Answers
These concepts form the basis of understanding electrical systems, allowing us to analyze and design complex circuits and devices.
Electricity is a form of energy resulting from charged particles, such as electrons and protons. Key electricity terminologies include:
1. Conductor: A material that allows the flow of electric charge with minimal resistance, typically metals like copper and aluminum.
2. Electrical circuit: A closed loop through which electric current flows, comprised of a power source, conductive path, and electrical components like resistors and capacitors.
3. Current: The flow of electric charge, measured in amperes (A). It is the rate at which charge moves through a circuit.
4. Voltage: The electric potential difference between two points, measured in volts (V). It represents the force driving electric charges through a circuit.
5. Resistance: The opposition to the flow of electric current, measured in ohms (Ω). Materials with higher resistance reduce the flow of current.
6. Watts: The unit of power, symbolized as 'W.' It represents the rate of energy transfer or conversion in an electrical circuit and is calculated by multiplying voltage (V) and current (A).
To know more about electricity visit:
https://brainly.com/question/12791045
#SPJ11
use the diagram to find each measure. please justify your solution with a postulate or theorem

Answers
Answer:
pandas
Step-by-step explanation:
An airplane makes the 2,400-mile trip from Washington, D. C. To San Francisco in 7. 5 hours and makes the return trip in 6 hours. Assuming that the plane travels at a constant airspeed and that the wind blows at a constant rate from west to east, we were asked to; (a) transform the problem into simultaneous equations. (b) transform the problem into a matrix equation. (c) find the plane’s airspeed and the wind rate
Answers
These equations represent the total distance traveled (2400 miles) being equal to the product of the effective speed (airplane's airspeed + wind rate) and the corresponding time taken.
(a) To transform the problem into simultaneous equations, let's denote the plane's airspeed as "p" and the wind rate as "w." Since the plane's speed is affected by the wind, we can set up the following equations:
For the Washington, D.C. to San Francisco trip:
2400 = (p + w) * 7.5
For the San Francisco to Washington, D.C. trip:
2400 = (p - w) * 6
(b) To transform the problem into a matrix equation, we can write the system of equations in matrix form:
⎡ 7.5 7.5 ⎤ ⎡ p ⎤ ⎡ 2400 ⎤
⎢ ⎥ ⎢ ⎥ = ⎢ ⎥
⎣ 6 -6 ⎦ ⎣ w ⎦ ⎣ 2400 ⎦
Here, the matrix on the left represents the coefficients of the variables (p and w), the column vector on the right represents the constants (2400), and the column vector in the middle represents the variables (p and w).
(c) To find the plane's airspeed (p) and the wind rate (w), we can solve the matrix equation using matrix operations. However, since the solution requires numerical calculations, it's not feasible to provide the exact values without additional information or calculations.
Know more about effective speedhere;
https://brainly.com/question/33111180
#SPJ11
Find the solution to this initial value problem. dy TU + 5 cot(5x) y = 3x³-1 csc(5x), y = 0 dx 10 Write the answer in the form y = f(x)
Answers
The solution to the initial value problem can be written in the form:
y(x) = (1/K)∫|sin(5x)|⁵ (3x³ - csc(5x)) dx
where K is a constant determined by the initial condition.
To solve the initial value problem and find the solution y(x), we can use the method of integrating factors.
Given: dy/dx + 5cot(5x)y = 3x³ - csc(5x), y = 0
Step 1: Recognize the linear first-order differential equation form
The given equation is in the form dy/dx + P(x)y = Q(x), where P(x) = 5cot(5x) and Q(x) = 3x³ - csc(5x).
Step 2: Determine the integrating factor
To find the integrating factor, we multiply the entire equation by the integrating factor, which is the exponential of the integral of P(x):
Integrating factor (IF) = e^{(∫ P(x) dx)}
In this case, P(x) = 5cot(5x), so we have:
IF = e^{(∫ 5cot(5x) dx)}
Step 3: Evaluate the integral in the integrating factor
∫ 5cot(5x) dx = 5∫cot(5x) dx = 5ln|sin(5x)| + C
Therefore, the integrating factor becomes:
IF = \(e^{(5ln|sin(5x)| + C)}\)
= \(e^C * e^{(5ln|sin(5x)|)}\)
= K|sin(5x)|⁵
where K =\(e^C\) is a constant.
Step 4: Multiply the original equation by the integrating factor
Multiplying the original equation by the integrating factor (K|sin(5x)|⁵), we have:
K|sin(5x)|⁵(dy/dx) + 5K|sin(5x)|⁵cot(5x)y = K|sin(5x)|⁵(3x³ - csc(5x))
Step 5: Simplify and integrate both sides
Using the product rule, the left side simplifies to:
(d/dx)(K|sin(5x)|⁵y) = K|sin(5x)|⁵(3x³ - csc(5x))
Integrating both sides with respect to x, we get:
∫(d/dx)(K|sin(5x)|⁵y) dx = ∫K|sin(5x)|⁵(3x³ - csc(5x)) dx
Integrating the left side:
K|sin(5x)|⁵y = ∫K|sin(5x)|⁵(3x³ - csc(5x)) dx
y = (1/K)∫|sin(5x)|⁵(3x³ - csc(5x)) dx
Step 6: Evaluate the integral
Evaluating the integral on the right side is a challenging task as it involves the integration of absolute values. The result will involve piecewise functions depending on the range of x. It is not possible to provide a simple explicit formula for y(x) in this case.
Therefore, the solution to the initial value problem can be written in the form: y(x) = (1/K)∫|sin(5x)|⁵(3x³ - csc(5x)) dx
where K is a constant determined by the initial condition.
To learn more about product rule visit:
brainly.com/question/29198114
#SPJ11