I complete lost on this problem can you help me solve it
The line described by y = 3/4x+5 is tangent to a circle at the point (0, 5). The line described by 3x + 4y = 38 is tangent to the same circle at the point (6, 5). Find the equation of the circle.
Answers
Answer:
(x-24/5)^2 + (y-21/5)^2 = (sqrt(481)/5)^2, or (x-24/5)^2 + (y-21/5)^2 = 481/25
Step-by-step explanation:
The equation of a circle can be written in the form (x-a)^2 + (y-b)^2 = r^2, where (a,b) is the center of the circle and r is its radius. Since the lines are tangent to the circle at points (0,5) and (6,5), we can use these points to find the center and radius of the circle.
First, let’s find the slope of each line. The slope of the line y = 3/4x+5 is 3/4. The slope of the line 3x + 4y = 38 can be found by rearranging it into slope-intercept form: y = (-3/4)x + 19/2. So the slope of this line is -3/4.
Since the lines are tangent to the circle, they are perpendicular to the radius at their point of tangency. This means that the center of the circle lies on the line that passes through (0,5) and has a slope of -4/3, and also on the line that passes through (6,5) and has a slope of 4/3.
Let’s find the equation of these two lines. The line passing through (0,5) with a slope of -4/3 has an equation y - 5 = (-4/3)(x - 0), or y = (-4/3)x + 5. The line passing through (6,5) with a slope of 4/3 has an equation y - 5 = (4/3)(x - 6), or y = (4/3)x - 3.
The center of the circle is at the intersection of these two lines. To find it, we can set their right-hand sides equal to each other and solve for x: (-4/3)x + 5 = (4/3)x - 3. Solving this equation gives us x = 24/5. Substituting this value into either equation for y gives us y = (4/3)(24/5) - 3 = 21/5.
So the center of the circle is at (24/5, 21/5). To find its radius, we can use either point of tangency. Let’s use (0,5). The distance between this point and the center is given by sqrt((0-24/5)^2 + (5-21/5)^2), which simplifies to sqrt(481)/5.
Therefore, the equation of the circle is (x-24/5)^2 + (y-21/5)^2 = (sqrt(481)/5)^2, or (x-24/5)^2 + (y-21/5)^2 = 481/25.
Related Questions
If g (t) has a continuous second derivative and f(x,y)= g(y)+tan^-1(xy), then f_xx(2,1)=
Answers
Compute the partial derivatives with respect to x :
\(f(x,y)=g(y)+\tan^{-1}(xy)\)
\(\implies f_x(x,y)=\dfrac y{1+(xy)^2}\)
\(\implies f_{xx}(x,y)=-\dfrac{2xy^3}{(1+(xy)^2)^2}\)
Evaluate the second partial derivative at (2, 1) :
\(\implies f_{xx}(x,y)=\boxed{-\dfrac4{25}}\)
what is the least common multiple 6 and 12
Answers
Answer:
12
Step-by-step explanation:
Lincoln Middle School had a canned food drive. The 6th graders brought in 5.75 boxes of canned food, the 7th graders brought in 6.5 boxes of canned food, and the Bth graders brought in 7 boxes of canned food. What was the total number of boxes of canned food brought in by the three grades?
Answers
Find the numbers with the following property three times the sum of four and a number is less than seven times the same number
Answers
Let's represent the number with the variable "x". According to the given property, we can write the following equation:
3(x + 4) < 7x
Now, let's solve this inequality to find the range of numbers that satisfy the property.
3x + 12 < 7x
Subtract 3x from both sides:
12 < 4x
Divide both sides by 4 (since the coefficient of x is 4):
3 < x
So, the range of numbers that satisfy the given property is x > 3.
Therefore, any number greater than 3 will satisfy the condition. For example, 4, 5, 6, 7, 8, etc.Step-by-step explanation:
According to the problem, we know that:
3(4 + x) < 7x
Simplifying:
12 + 3x < 7x
Subtracting 3x from both sides:
12 < 4x
Dividing both sides by 4:
3 < x
So the number we're looking for must be greater than 3.
Find an equation of the line, and write it in (a) slope-intercept form if possible and (b) standard form.

Answers
1) Note that we need to find a perpendicular line. Perpendicular lines have reciprocal and opposite slopes. So we know that the slope we need is -3
2) We also know that it must pass through (-2,-6), so let's plug the slope -3 the point (-2,-6) so that we can find the linear coefficient:
\(\begin{gathered} y=mx+b \\ -6=-3(-2)+b \\ -6=6+b \\ -6-6=b \\ b=-12 \end{gathered}\)
Olivia measures the heights of two trees and the lengths of their shadows. She notices that the height of each tree and the length of its shadow are directly proportional. One of the trees has a height of 15 m and a 10 m long shadow. The other tree has a 14.4 m long shadow. Calculate its height, in metres (m). Give any decimal answers to 1 d.p. 15 m 10 m ? m 14.4 m
Answers
Step-by-step explanation:
directly proportional means
y = kx
with k being a constant factor for all values of x.
we get k by using the given data point (10, 15).
15 = k×10
k = 15/10 = 1.5
so, now for the other tree we know k and x and calculate y
y = 1.5×14.4 = 21.6 m
it is 21.6 m tall (its height is 21.6 m).
√√96
√8
Ο 213
Ο 4
Ο 222
D. 12

Answers
Answer:
2sqr3, the first option
Step-by-step explanation:
ill marki brainlist plss help

Answers
Answer:
It's answer is rhombus .
The quadrilateral having 4 congruent sides is rhombus.
Hope it will help :)❤
If the figure below is a regular polygon, find the value of x.
(9x - 18)
Answers

Why is a third-degree polynomial function with a negative leading coefficient not appropriate for modeling non-negative real-world phenomena over a long period of time?
Answers
Given:
A third-degree polynomial function with a negative leading coefficient not appropriate for modeling non-negative real-world phenomena over a long period of time.
Explanation:
Because a third-degree polynomial function with a negative leading coefficient is always going to turn negative as the independent variable increases.
That is, the end behavior of the graph will always be negative on the right.
Final Answer:
Because a third-degree polynomial function with a negative leading coefficient is always going to turn negative as the independent variable increases.
That is, the end behavior of the graph will always be negative on the right.
If f(x) = 2x + 10, then f-'(x) =
Answers
We need to find the inverse of the function:
\(f(x)=2x+10\)First step:
replace f(x) with a letter (y for example):
\(=2x+10\)y = 2x +10 (the equation editor is not allowing me to enter a "y" for some reason)
Second step:
solve for x:
2x = y - 10
x = (y - 10)/2
Third step:
replace x with f^-1(x), and replace y with x:
\(f^{-1}(x)=\frac{x-10}{2}=\frac{x}{2}-5\)the inverse is: (1/2) x - 5
or equivalently: (x-10)/ 2 that is: (x minus 10) divided by 2
The sum of half of a number and 49 is 2 1/4 of the number. Find the number
Answers
Answer:
x = 28
Step-by-step explanation:
given, x/2 + 49 = 21/4
x/2 + 49 = 9x/4
2x +196 = 9x
7x = 196
x = 28
I hope this helps a little bit.
Blake has a glass tank. First, he wants to put some marbles in it, all of the same volume. Then, he wants to fill the tank with water until it's completely full. The equation shown below describes the volume of water, W, measured in liters, that Blake should use when there are n marbles. What is the volume of the glass tank, in liters?
W=32−0.05n
Answers
Answer:
32 liters is the volume of the glass tank
what is the approximate solution of the linear system represented by the graph below

Answers
The approximate solution of the linear system represented by the graph is, (5, 6)
What is the equation of line?The equation of a straight line is a relationship between x and y coordinates, The general equation of a straight line is y = mx + c, where m is the slope of the line and c is the y-intercept.
Given that,
A graph in which two lines are intersecting each other,
basically solution of linear system means where both the lines will intersect,
So, in the graph it can be seen that lines are intersecting around x coordinate 5 and y coordinate 6,
Therefore, the solution is (5, 6)
To know more about Line check:
https://brainly.com/question/17188072
#SPJ1
Can you guys help me with this question? thanks so much!
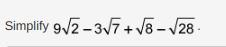
Answers
Answer:
11√2 - 5√7
Step-by-step explanation:
For the function f(x)=x+4−−−−−√
, the average rate of change to the nearest hundredth over the interval 2 ≤ x ≤ 6 is
Answers
The average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6 is approximately 0.29 to the nearest hundredth.
To find the average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6, we need to calculate the change in the function divided by the change in the input variable over that interval.
The change in the function between x = 2 and x = 6 is:
f(6) - f(2) = √(6+4) - √(2+4) = √10 - √6
The change in the input variable between x = 2 and x = 6 is:
6 - 2 = 4
So, the average rate of change of the function over the interval 2 ≤ x ≤ 6 is:
(√10 - √6) / 4
To approximate the answer to the nearest hundredth, we can use a calculator or perform long division to get:
(√10 - √6) / 4 ≈ 0.29
For such more questions on function
https://brainly.com/question/11624077
#SPJ8
If each quadrilateral below is a kite, find the missing measures.

Answers
Answer:
F and H are both 121 degrees
Step-by-step explanation:
"A kite has 4 interior angles and the sum of these interior angles is 360°. In these angles, it has one pair of opposite angles that are obtuse angles and are equal." - Cue math
Ok, so the two acute angles add up to 118 degrees, and in order to find the remaining angles we need, subtract 118 from 360 to get 242. Because the two obtuse angles are equivalent, divide 242 by 2 to get the measure of each.
given that triangle DEF is a right triangle with acute angles D and F and right angle E, which trigonometric function would be equal to Sin(F).

Answers
EXPLANATION
We can represent this situation as shown as follows:
The expression of Sin(F) is equal to Sin F = Opposite/Hypotenuse = DE/DF
\(\sin F=\frac{Opposite}{\text{Hypotenuse}}=\frac{DE}{DF}\)The equivalent expression would be:
\(Cos\text{ D=}\frac{Adjacent}{\text{Hypotenuse}}=\frac{DE}{DF}\)
The price of a car has been reduced from $16,500 to $11,055. What is the percentage decrease of the price of the car?
Answers
Answer:
33%
Step-by-step explanation:
$16,500-$11,055= $5,445
$5,445÷$16,500= 0.33 which in percentage format is 33%
HOPE THIS HELPS! MARK BRAINLIEST PLEASE!!!!!
Brandon invests $5800 in two different accounts. The first account paid 3 %, the second account paid 8 % in interest. At the end of the first year he had earned $229 in interest. How much was in each account?
$ ___ at 3 %
$ ____ at 8 %
Answers
Brandon invested $4700 at 3% interest and $1100 at 8% interest using a linear equation.
In mathematics, what exactly is a linear equation?An algebraic equation of the form y=mx+b is a linear equation. m is the slant and b is the y-capture. A "linear equation in two variables" with y and x as variables is sometimes referred to as the one above.
A linear equation is one in which a variable is raised to its first power. One example of a one variable is ax+b = 0. x is a variable and an and b are genuine numbers.
Let x represent the amount invested in the first account, which earns interest at a rate of 3%, and let y represent the amount invested in the second account, which earns interest at a rate of 8%. Since the aggregate sum contributed is $5800, we have:
x + y = 5800 The first account has earned 0.03x in interest, while the second account has earned 0.08y in interest. After one year, we have earned $229 in total interest, so we have:
We now have two equations with two unknowns: 0.03x + 0.08y = 229
We can solve for x and y using either the elimination or substitution method. x + y = 5800. In this instance, we will employ substitution.
Find a solution to the first x-equation:
x = 5800 - y
Substitute this expression for x:
0.03(5800 - y) + 0.08y = 229
174 - 0.03y + 0.08y = 229
0.05y = 55
y = 1100
Now substitute this value of y into either equation to solve for x
x + 1100 = 5800
x = 4700
Learn more about linear equation:
brainly.com/question/11897796
#SPJ1
How are factors and products connected
Answers
the population in the town increased 5000 million per year. if the population is 120000 three years ago.. what is the population now
Answers
Answer:
The population will be 135000
5000 x 3 = 15000
Then you add 120000 with 15000
Carns Company is considering eliminating its Small Tools Division, which reported a loss for the prior year of $205,000 as shown below. Segment Income (Loss) Sales $ 1,430,000 Variable costs 1,295,000 Contribution margin 135,000 Fixed costs 340,000 Income (loss) $ (205,000) If the Small Tools Division is dropped, all of its variable costs are avoidable, and $119,000 of its fixed costs are avoidable. The impact on Carns’s income from eliminating the Small Tools Division would be: Multiple Choice
Answers
The impact on Carns Company's income from eliminating the Small Tools Division would be a decrease of $1,209,000.
To determine the impact on Carns Company's income from eliminating the Small Tools Division, we need to consider the avoidable costs associated with the division.
The avoidable costs include all of the variable costs of the division and a portion of the fixed costs that are specifically related to the Small Tools Division. In this case, the variable costs of the division are $1,295,000, and $119,000 of the fixed costs are avoidable.
To calculate the impact on income, we subtract the avoidable costs from the loss reported by the division:
Impact on income = Loss - Avoidable costs
Impact on income = $205,000 - ($1,295,000 + $119,000)
Impact on income = $205,000 - $1,414,000
Impact on income = -$1,209,000
The negative sign indicates a decrease in income.
For more such questions on income
https://brainly.com/question/28414951
#SPJ8
The expected value of a random variable X is 62. The variable is transformed by multiplying X by 3 and then adding 6 to it. Find the expected value (mean) of the transformed variable.A.192B.156C.103D.205
Answers
SOLUTION
The random variable x is
\(x=62\)Multiplying X by 3 and then adding 6 to it.
\(\begin{gathered} x\times3+6 \\ 3x+6 \\ \end{gathered}\)Since
\(\begin{gathered} x=62 \\ 3\times62+6 \\ 186+6 \\ =192 \end{gathered}\)Hence
The expected value of the transformed variable is 192
The right option is A.
Order the five ratios from least to greatest.
1/5
2:12
1:1
5/3
25/100
Answers
Step-by-step explanation:
Order the five ratios from least to greatest.
1/5 = 0.2
2:12 = 0.166667
1:1 = 1
5/3 = 1.66667
25/100 = 0.25
Answer:
5/3 , 1:1 , 25/100 , 1/5 , 2:12
Which part of the angle is the vertex?
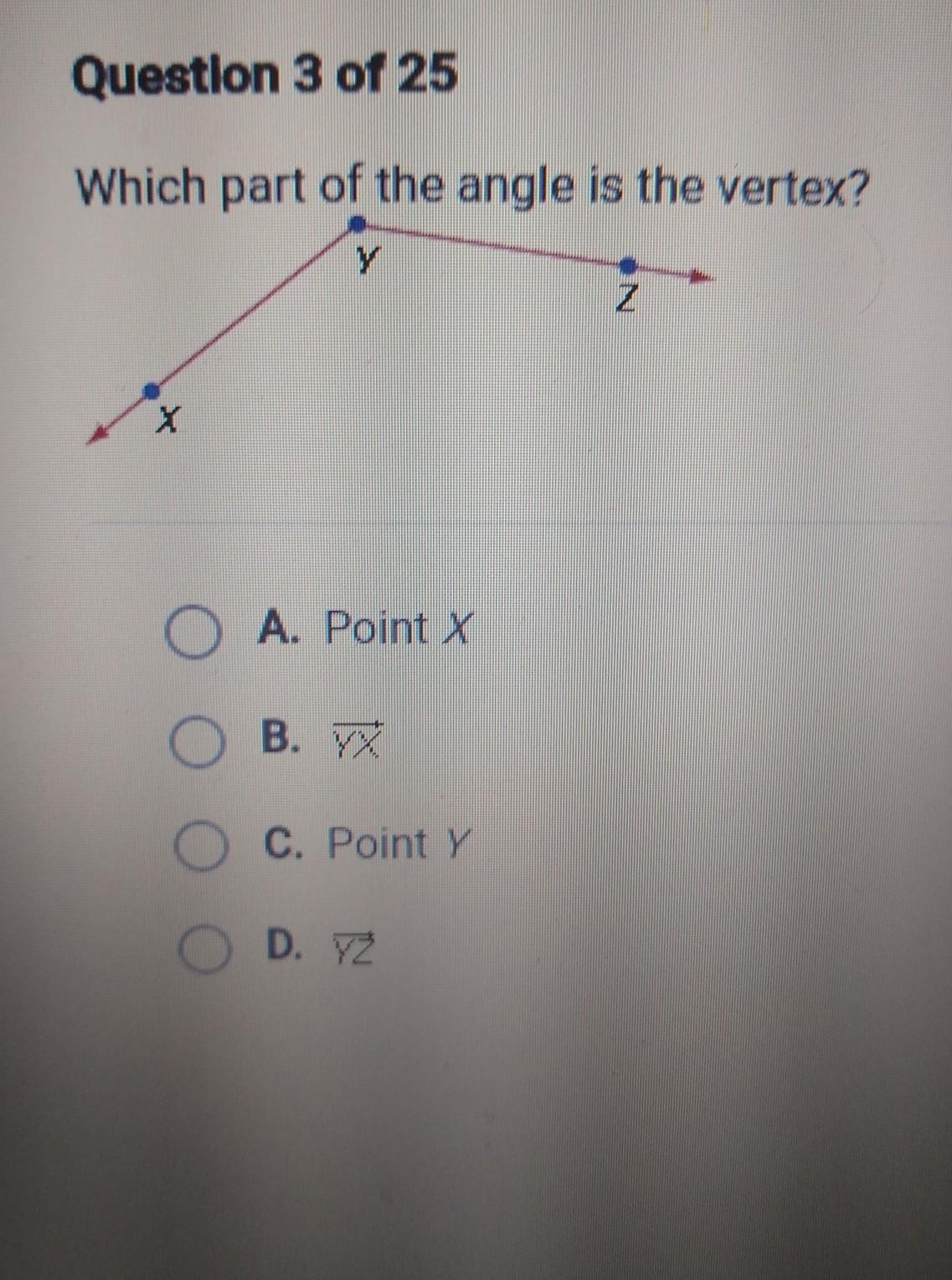
Answers
Answer:
the answer is point Y since it is in the middle of the line between X and Z
Answer:
Point Y
Step-by-step explanation:
Always the lines which intersect at a point, that point is called vertex.
Type the correct answer in each box.Consider the expressions shown below.

Answers
The first expression is
\((3x^2-6x+11)-(10x^2-4x+6)\)First, we use the distributive property
\(3x^2-6x+11-10x^2+4x-6\)Then, we combine like terms
\(-7x^2-2x+5\)The first answer is A.The second expression is
\(\begin{gathered} (-3x^2-5x-3)-(-10x^2-7x+2) \\ -3x^2-5x-3+10x^2+7x-2 \\ 7x^2+2x-5 \end{gathered}\)The second answer is C.The third expression is
\(\begin{gathered} (12x^2+6x-5)-(5x^2+8x-12) \\ 12x^2+6x-5-5x^2-8x+12 \\ 7x^2-2x+7 \end{gathered}\)The third answer is B.If you can walk 4.9 miles in 2.9 hours, how many minutes does it take to walk 8.73 miles? Round to 1 decimal.
Answers
Step-by-step explanation:
2.9 hours = 174mins
174 mins = 4.9miles
1 miles = 1740/49 mins
8.73 miles = 310.0mins (1dp)
Topic: Rate & Proportions
If you like to venture further, do check out my insta (learntionary) where I regularly post useful math tips! Thank you!
A student takes a subway to a public library. The table shows the distance d (in miles) the student travels in t minutes. Determine whether the data can be modeled by a linear, exponential, or a quadratic function and then select a function rule to model the situation.
t
d
1
0.83
2
1.66
3
2.49
4
3.32
5
4.15
Answers
The linear function that models the situation is given as follows:
d = 0.85t.
What is a proportional relationship?A proportional relationship is a relationship in which a constant ratio between the output variable and the input variable is present.
The equation that defines the proportional relationship is a linear function with slope k and intercept zero given as follows:
y = kx.
The slope k is the constant of proportionality, representing the increase or decrease in the output variable y when the constant variable x is increased by one.
The constant ratio for this problem is given as follows:
k = 0.83, as each division of d by t has a result of 0.83.
Hence the equation is given as follows:
d = 0.83t.
A similar problem, also featuring proportional relationships, is presented at https://brainly.com/question/7723640
#SPJ1
The solid below is dilated by a scale factor of 4. Find the volume of the solid created
upon dilation. Answer in terms of TT.
Answer:
units³
3
Submit Answer

Answers
Step-by-step explanation:
the volume of a sphere is
4/3 × pi × r³
the original sphere had a radius of 3.
now, after a dilation of factor 4 the radius is 3×4 = 12.
the volume of that sphere is then
4/3 × pi × 12³ = 4/3 × pi × 1728 = 2304pi