Answers
Answer:f(x)=2x3^x
Step-by-step explanation:
Related Questions
What is the initial value of the function represented by this graph
A. 0
B. 1
C. 2
D. 5

Answers
Answer:
2 because the initial value is y-intercept
in a batch of pedometers, are believed to be defective. a quality-control engineer randomly selects units to test. let random variable xthe number of defective units that are among the units tested. a. find the probability mass function f(x)p(xx), and sketch its histogram. b. find p(x1). what does this number represent? c. find p(x1). what does this number represent?
Answers
We found the PMF f(x), calculated the probability of selecting exactly one defective unit, and determined the probability of selecting more than one defective unit.
To find the probability mass function (PMF) f(x) for the number of defective units, we need to determine the probability of each possible outcome.
Let's assume that the total number of units tested is n. Since it is mentioned that 2% of the units are defective, the probability of selecting a defective unit is 0.02.
The PMF f(x) can be calculated using the binomial distribution formula:
\(f(x) = C(n, x) * (0.02)^x * (0.98)^(n-x)\)
To find p(x=1), we substitute x=1 into the PMF formula:
\(f(1) = C(n, 1) * (0.02)^1 * (0.98)^(n-1)\)
This represents the probability of selecting exactly one defective unit when testing a batch of pedometers.
Similarly, to find p(x>1), we need to sum up the probabilities for x=2, x=3, and so on, up to x=n:
\(p(x>1) = f(2) + f(3) + ... + f(n)\)
This represents the probability of selecting more than one defective unit when testing a batch of pedometers.
To sketch the histogram, we can plot the values of x on the x-axis and the corresponding probabilities f(x) on the y-axis. Each bar's height represents the probability of selecting that many defective units.
In conclusion, we found the PMF f(x), calculated the probability of selecting exactly one defective unit, and determined the probability of selecting more than one defective unit.
To know more about probability visit:
brainly.com/question/31828911
#SPJ11
What is the sum? StartFraction 3 y Over y squared 7 y 10 EndFraction StartFraction 2 Over y 2 EndFraction.
Answers
You can take LCM and then can add to see what's the sum.
The sum result of given expressions is given by: \(\dfrac{5}{y+5}\)
Given that:To find sum of \(\dfrac{3y}{y^2 + 7y + 10}\) and \(\dfrac{2}{y+2}\)Finding LCM and summing:You can take LCM and then can add to see whats the sum.
\(\begin{aligned}\dfrac{3y}{y^2 + 7y + 10} + \dfrac{2}{y+2} &= \dfrac{3y}{(y+2)(y+5)} + \dfrac{2}{y+2}\\&= \dfrac{3y + 2(y+5)}{(y+2)(y+5)}\\&= \dfrac{5y+10}{(y+2)(y+5)}\\&= \dfrac{5(y+2)}{(y+2)(y+5)}\\&= \dfrac{5}{y+5}\\\end{aligned}\)
Thus, the sum of given expressions is given by:
\(\dfrac{5}{y+5}\)
Learn more about algebraic sums here:
https://brainly.com/question/14964662
PLS I NEED HELP WITH THIS!!!!

Answers
Answer:
Step-by-step explanation:
The volume of a cylinder is
\(V=h\pi r^2\\ \\ h=8,\ r=4\\ \\ V=8\pi (4^2)\\ \\ V=8(16)\pi \\ \\ V=128\pi \units^3\)
How many square meters are in 280 square centimeters
Answers
We can perform a change of units to see that 280 square centimeters is equivalent to 0.028 square meters.
How many square meters are in 280 square centimeters?We want to perform a change of units between square centimeters and meters.
Remember the relation:
100cm = 1m
Now we can square both sides of that equation, then we will get:
(100 cm)^2 = (1m)^2
10,000 cm^2 = 1m^2
Then if we have a measure in square centimeters, to transform it into square meters we need to divide that measure by 10,000.
Then:
280 cm^2 = (280/10,000) m^2 = 0.028 m^2
Learn more about changes of units at:
https://brainly.com/question/141163
#SPJ1
!!!SOMEONE PLEASE HELP ME THIS IS URJENT!!!
- will mark brainliest!!
- 20 POINTS!!
Answers
Answer:
What do you need help with?
Step-by-step explanation:
Answer:
Eat dino nuggies
Step-by-step explanation:
and r(x) = 3x² If P(x)=x²-3x²-1/2 x + 10, Q(x) = ²x² - 1x ²-1/2 X- subtract R(x) from the sum of P(x) and Q(x). 6x + 1 then find p(x) + q(x) - r(x). 3 5 and R(x) - 34 X + the 4X
Answers
Answer:Z
cos x dx = sin x + C
Z
sec2 x dx = tan x + C
Z
sec x tan x dx = sec x + C
Z
1
1 + x2
dx = arctan x + C
Z
1
√
1 − x2
dx = arcsin x + C
8.1 Substitution
Needless to say, most problems we encounter will not be so simple. Here’s a slightly more
complicated example: find
Z
2x cos(x
2
) dx.
This is not a “simple” derivative, but a little thought reveals that it must have come from
an application of the chain rule. Multiplied on the “outside” is 2x, which is the derivative
of the “inside” function x
2
. Checking:
d
dx sin(x
2
) = cos(x
2
)
d
dxx
2 = 2x cos(x
2
),
so Z
2x cos(x
2
) dx = sin(x
2
) + C.
Even when the chain rule has “produced” a certain derivative, it is not always easy to
see. Consider this problem:
Z
x
3
p
1 − x
2 dx.
There are two factors in this expression, x
3
and p
1 − x
2, but it is not apparent that the
chain rule is involved. Some clever rearrangement reveals that it is:
Z
x
3
p
1 − x
2 dx =
Z
(−2x)
−
1
2
(1 − (1 − x
2
))p
1 − x
2 dx.
This looks messy, but we do now have something that looks like the result of the chain
rule: the function 1 − x
2 has been substituted into −(1/2)(1 − x)
√
x, and the derivative
Step-by-step explanation:Z
cos x dx = sin x + C
Z
sec2 x dx = tan x + C
Z
sec x tan x dx = sec x + C
Z
1
1 + x2
dx = arctan x + C
Z
1
√
1 − x2
dx = arcsin x + C
8.1 Substitution
Needless to say, most problems we encounter will not be so simple. Here’s a slightly more
complicated example: find
Z
2x cos(x
2
) dx.
This is not a “simple” derivative, but a little thought reveals that it must have come from
an application of the chain rule. Multiplied on the “outside” is 2x, which is the derivative
of the “inside” function x
2
. Checking:
d
dx sin(x
2
) = cos(x
2
)
d
dxx
2 = 2x cos(x
2
),
so Z
2x cos(x
2
) dx = sin(x
2
) + C.
Even when the chain rule has “produced” a certain derivative, it is not always easy to
see. Consider this problem:
Z
x
3
p
1 − x
2 dx.
There are two factors in this expression, x
3
and p
1 − x
2, but it is not apparent that the
chain rule is involved. Some clever rearrangement reveals that it is:
Z
x
3
p
1 − x
2 dx =
Z
(−2x)
−
1
2
(1 − (1 − x
2
))p
1 − x
2 dx.
This looks messy, but we do now have something that looks like the result of the chain
rule: the function 1 − x
2 has been substituted into −(1/2)(1 − x)
√
x, and the derivative
Please answer the questions at the top.

Answers
Answer: Let's be honest, no one knows the answer. Unless you want to pay coursehero $9.95/mo for an answer and step-by-step explanation, you're toast.
Some of my answers are absolutely amazing, and actually helpful. But some of my answers are not.
A lot of the time, Brainly's "Expert Verified Answers" are very incorrect, and even if you report it, Brainly does not care.
So, if Brainly ITSELF can't answer a question properly, well,
Simply put, your grade is toast.
And if Brainly deletes this absolutely wonderful fantastic answer, that just means that they are acknowledging that these "Expert Verified Answers" are not as "expert" as they may think they are.
:|
simplify the square root 1×46÷75
Answers
Answer:
√48/75, I think.
Step-by-step explanation:
Not quite sure.
Answer:
\(\sqrt{\frac{46}{75} }\)
Step-by-step explanation:
\(\sqrt{1 \times 46 \div 75}\)
Simplify.
\(\sqrt{\frac{46}{75} }\)
Suppose that X and Y have a discrete joint distribution for which the joint probability mass function (pmf) is f X,Y
(x,y)={ c∣x+y∣
0
if x,y∈{−2,−1,0,1,2}
otherwise.
Determine: (a) the value of the constant c; (b) P(X=0 and Y=2); (c) the (marginal) distribution of the random variable X; and (d) P(∣X−Y∣≤1)
Answers
P(|X-Y|≤1) = P(X=Y) + P(|X-Y| = 1) = 6/25 + 6/25 = 12/25 Answer: a) c=1/25; b) P(X=0 and Y=2)=2/25;
a) The probability mass function (PMF) is given as;f X,Y
(x,y)={ c∣x+y∣
0
if x,y∈{−2,−1,0,1,2}
otherwise.
For a joint PMF, the sum of probabilities across all x and y must be equal to 1. Therefore;∑∑f X,Y
(x,y)=1
The sum of the probabilities when (x,y) is not an element of {−2,−1,0,1,2} is zero, and there are 25 other possibilities. When |x+y| = 0, there are four possibilities: (0, 0), (−1, 1), (1, −1) and (2, −2).∑∑f X,Y
(x,y)=4c+4c+4c+3c+4c+3c+2c+2c+2c+1c+1c+0+1c+2c+3c+4c+3c+4c+4c+4c+0+4c+4c+4c=25
c=1
Hence, the value of the constant c is; c=1/25
b) For P(X = 0 and Y = 2), there is only one possibility, and that is when X = 0 and Y = 2. Therefore;P(X = 0 and Y = 2) = f X,Y
(0,2) = c|0+2| = c×2 = 2/25
c) The marginal distribution of X is given as;f X
(x)=∑yf X,Y
(x,y)
The possible values of X are -2, -1, 0, 1, 2. The probabilities are as follows:
For x = -2, f X
(-2) = (0+0+0+0+1)c = c
For x = -1, f X
(-1) = (0+0+0+1+2)c = 3c
For x = 0, f X
(0) = (0+0+1+2+1)c = 4c
For x = 1, f X
(1) = (0+1+2+1+0)c = 4c
For x = 2, f X
(2) = (1+2+1+0+0)c = 4c
Hence, the marginal distribution of the random variable X is given by;f X
(-2) = 1/25, f X
(-1) = 3/25, f X
(0) = 4/25, f X
(1) = 4/25, f X
(2) = 4/25
d) To evaluate P(|X-Y|≤1), we consider the cases where |X-Y| = 0 or 1. When |X-Y| = 0, this means that X = Y. Therefore;P(X = Y) = ∑xP(X = x and Y = x) = f X,Y
(−2,−2)+f X,Y
(−1,−1)+f X,Y
(0,0)+f X,Y
(1,1)+f X,Y
(2,2)
= (1+2+1+1+1)c = 6c = 6/25
When |X-Y| = 1, there are four possible pairs; (−1,0), (0,−1), (0,1) and (1,0).P(|X-Y| = 1) = ∑i∑jP(X = i and Y = j) where i and j are any two of −1, 0, 1
= f X,Y
(−1,0)+f X,Y
(0,−1)+f X,Y
(0,1)+f X,Y
(1,0)
= (0+0+2+2+2)c = 6c = 6/25
c) The marginal distribution of X is given by; f X
(-2) = 1/25, f X
(-1) = 3/25, f X
(0) = 4/25, f X
(1) = 4/25, f X
(2) = 4/25; d) P(|X-Y|≤1)=12/25
To learn more on probability mass function :
https://brainly.com/question/30765833
#SPJ11
find a basis for each of the subspaces r(at), n (a), r(a), n (at).
Answers
The specific solution depends on the given matrix A.
To find a basis for each of the subspaces r(AT), N(A), r(A), and N(AT), we first need to understand what each of these terms represents:
1. r(AT) - the row space of the transpose of matrix A
2. N(A) - the null space of matrix A
3. r(A) - the row space of matrix A
4. N(AT) - the null space of the transpose of matrix A
To find a basis for each of these subspaces, follow these general steps:
1. For r(A) and r(AT), row reduce the matrix A and its transpose AT to their row echelon forms. The non-zero rows in the reduced matrices will form a basis for the row spaces.
2. For N(A) and N(AT), set up the homogenous system of linear equations (Ax = 0 and ATx = 0), where x is the vector of variables. Then, solve the systems using Gaussian elimination, and find the general solutions. The general solutions will provide the basis vectors for the null spaces.
Note that specific solutions depend on the given matrix A. The process outlined above will help you find the basis for each of the subspaces r(AT), N(A), r(A), and N(AT) once you have the matrix A.
The correct question should be :
What is the matrix A for which you would like to find the basis for each of the subspaces r(AT), N(A), r(A), and N(AT)?
To learn more about subspaces visit : https://brainly.com/question/13045843
#SPJ11
Write the coordinates of the verticals after a rotation 270 counter clockwise around the origin
D=
E=
F=
G=

Answers
Check the picture below.

please graph y≤ 2x-3
Answers

Math practice for math tmr
Graph:

Answers
Answer:
its 1/2
Step-by-step explanation:
Answer:
math
Step-by-step explanation:
d/d{cosec^-1(1+x²/2x)} is equal to

Answers
Step-by-step explanation:
\(\large\underline{\sf{Solution-}}\)
\(\rm :\longmapsto\:\dfrac{d}{dx} {cosec}^{ - 1} \bigg( \dfrac{1 + {x}^{2} }{2x} \bigg)\)
Let assume that
\(\rm :\longmapsto\:y = {cosec}^{ - 1} \bigg( \dfrac{1 + {x}^{2} }{2x} \bigg)\)
We know,
\(\boxed{\tt{ {cosec}^{ - 1}x = {sin}^{ - 1}\bigg( \dfrac{1}{x} \bigg)}}\)
So, using this, we get
\(\rm :\longmapsto\:y = sin^{ - 1} \bigg( \dfrac{2x}{1 + {x}^{2} } \bigg)\)
Now, we use Method of Substitution, So we substitute
\( \red{\rm :\longmapsto\:x = tanz \: \rm\implies \:z = {tan}^{ - 1}x}\)
So, above expression can be rewritten as
\(\rm :\longmapsto\:y = sin^{ - 1} \bigg( \dfrac{2tanz}{1 + {tan}^{2} z} \bigg)\)
\(\rm :\longmapsto\:y = sin^{ - 1} \bigg( sin2z \bigg)\)
\(\rm\implies \:y = 2z\)
\(\bf\implies \:y = 2 {tan}^{ - 1}x\)
So,
\(\bf\implies \: {cosec}^{ - 1}\bigg( \dfrac{1 + {x}^{2} }{2x} \bigg) = 2 {tan}^{ - 1}x\)
Thus,
\(\rm :\longmapsto\:\dfrac{d}{dx} {cosec}^{ - 1} \bigg( \dfrac{1 + {x}^{2} }{2x} \bigg)\)
\(\rm \: = \: \dfrac{d}{dx}(2 {tan}^{ - 1}x)\)
\(\rm \: = \: 2 \: \dfrac{d}{dx}( {tan}^{ - 1}x)\)
\(\rm \: = \: 2 \times \dfrac{1}{1 + {x}^{2} } \)
\(\rm \: = \: \dfrac{2}{1 + {x}^{2} } \)
Hence,
\( \purple{\rm :\longmapsto\:\boxed{\tt{ \dfrac{d}{dx} {cosec}^{ - 1} \bigg( \dfrac{1 + {x}^{2} }{2x} \bigg) = \frac{2}{1 + {x}^{2} }}}}\)
Hence, Option (d) is correct.
find the radius of convergence and interval of convergence of the series x[infinity] n=1 2 · 4 · 6 · · · 2n 3 · 5 · 7 · · ·(2n 1) x 2n 1 .
Answers
The radius of convergence is 0, and the interval of convergence is the single point x = 0.
To obtain the radius of convergence and interval of convergence of the series we can use the ratio test.
\(\[ \sum_{n=1}^{\infty} \frac{2 \cdot 4 \cdot 6 \cdots (2n)}{3 \cdot 5 \cdot 7 \cdots (2n+1)}x^{2n+1} \]\)
The ratio test states that if \(\( L = \lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| \)\), then the series converges if \(\( L < 1 \)\) and diverges if \(\( L > 1 \). If \( L = 1 \)\), the test is inconclusive.
Let's calculate the limit:
\(\[ L = \lim_{n \to \infty} \left| \frac{\frac{2 \cdot 4 \cdot 6 \cdots (2(n+1))}{3 \cdot 5 \cdot 7 \cdots (2(n+1)+1)}x^{2(n+1)+1}}{\frac{2 \cdot 4 \cdot 6 \cdots (2n)}{3 \cdot 5 \cdot 7 \cdots (2n+1)}x^{2n+1}} \right| \]\)
Simplifying the expression:
\(\[ L = \lim_{n \to \infty} \left| \frac{(2n+2)(2n+1)x^{2n+3}}{(2n+1)(2n)x^{2n+1}} \right| \]\)
\(\[ L = \lim_{n \to \infty} \left| \frac{(2n+2)x^2}{x^2} \right| \]\)
\(\[ L = \lim_{n \to \infty} 2(n+1) = \infty \]\\\)
Since the limit is infinity, the series diverges for all values of x , except when x = 0 and hence the radius of convergence is 0, and the interval of convergence is the single point x = 0.
To know more about radius of convergence refer here:
https://brainly.com/question/32608353#
#SPJ11
Please ASAP Help
Will mark brainlest due at 12:00

Answers
The coordinates of the midpoint of the given segment is; (-15, 4)
How to find the midpoint of the coordinates?For any specific line segment, it is well known that the midpoint is defined as the halfway between its two endpoints. The expression that is used to find the x-coordinate of that midpoint is expressed as: [(x)1 + (x)2]/2, which denotes the average of the x-coordinates. Similarly, the expression that is used to find the y-coordinate of that midpoint is expressed as: [(y)1 + (y)2]/2, which is the average of the y-coordinates.
We are given the coordinates of the endpoints of the line as;
K(-11, 2) and L(-19, 6)
Thus;
Midpoint Coordinate = (-11 - 19)/2, (2 + 6)/2
= (-15, 4)
Read more about coordinate midpoint at; https://brainly.com/question/5566419
#SPJ1
does anybody know how to solve this problem? -
30 - 2(3²+5)
Answers
Answer:
2
Step-by-step explanation:
BIDMAS
(Brackets, Indices, division, multiply, add, sub)
so lets do the bracket first
(3^2+5)
We treat this as another question so we do 3^2 which is 9, 9+5=14
30 - 2(14)
we then multiply
30-28
finally subtract = 2
Answer:
2
Step-by-step explanation:
\(30-2(3^2+5)\\=30-2(9+5)\\=30-2(14)\\=30-28\\=2\)
Remember PEMDAS (Parentheses, Exponents, Multiplication/Division left to right, Addition/Subtraction left to right)
he
2
2
63
Paula is standing on a bridge that is 110 above
the water below. She throws a pebble over
the edge of the bridge, and it hits the top of a
24 foot high bridge guard. The quadratic
equation that models the path of the pebble is:
p(t) = -16t² + 48t + 110
such that t is the time in seconds and p is
the height of the pebble.
What is the maximum height of the
pebble?
A) 2 feet
(B) 146 feet
C110 feet
D) 210 feet
Answers
Answer:
(B) 146 feet
Step-by-step explanation:
You want to know the maximum height of a pebble whose height is described by p(t) = -16t² + 48t + 110.
Vertex formWe can write the equation in vertex form as follows:
p(t) = -16(t² -3t) +110
p(t) = -16(t² -3t +2.25) +110 +16(2.25)
p(t) = -16(t -1.5)² +146
This shows the vertex of the quadratic curve to be (1.5, 146).
The maximum height of the pebble is 146 feet.

The temperature this morning was 15.70F. At 4pm, the temperature was 59.20F. What was the change in temperature?
Answers
Answer:
43.5F
Step-by-step explanation:
All you need to do is subtract 15.70 from 59.20
Find the average value of the function f over the given region.
-f(x, y) = 8x + 5y over the triangle with vertices (0, 0), (2, 0), and (0, 7).
A) 23/3 B) 7
C) 16/3
D) 17
Answers
To find the average value of the function f(x, y) = 8x + 5y over the given triangle, we need to calculate the double integral of f(x, y) over the region and then divide it by the area of the triangle.
The vertices of the triangle are (0, 0), (2, 0), and (0, 7). We can set up the integral as follows:
∬R f(x, y) dA = ∫₀² ∫₀ᵧ (8x + 5y) dy dx
Integrating with respect to y first, the inner integral becomes:
∫₀ᵧ (8x + 5y) dy = 8xy + (5y²/2) |₀ᵧ = 8xᵧ + (5ᵧ²/2)
Now integrating with respect to x, the outer integral becomes:
∫₀² (8xᵧ + (5ᵧ²/2)) dx = (4x²ᵧ + (5ᵧ²x)/2) |₀² = (8ᵧ + 10ᵧ² + 20ᵧ)
To find the area of the triangle, we can use the formula for the area of a triangle: A = (1/2) * base * height.
The base of the triangle is 2 and the height is 7.
A = (1/2) * 2 * 7 = 7
Finally, to find the average value, we divide the double integral by the area of the triangle:
Average value = (8ᵧ + 10ᵧ² + 20ᵧ) / 7
Simplifying this expression gives:
Average value = (8 + 10ᵧ + 20ᵧ) / 7 = (8 + 10(7) + 20(7)) / 7 = 142/7 = 20 2/7
Therefore, the correct answer is not listed among the options provided.
Learn more about vertices here: brainly.com/question/32263629
#SPJ11
help please
plz plz plz

Answers
Step-by-step explanation:
Here,
y= 2x
and x € (1,2,3)
now,
when x=1 , when x=2 , when x= 3
y=2x y= 2x y=2x
= 2×1 = 2×2 = 2×3
= 2 = 4 = 6
Therefore, y = (2,3,6)
WORK PROBLEMS Ted can mow the lawn in 5 minutes by using his power mower. Galen takes 15 minutes to mow the same lawn using a push-type mower. How many minutes would the job take if the two boys worked together
Answers
Ted can mow the lawn in 5 minutes by using his power mower. Galen takes 15 minutes to mow the same lawn using a push-type mower.
Let's calculate the amount of work done by Ted in 1 minute.WORK = 1/5Let's calculate the amount of work done by Galen in 1 minute.WORK = 1/15
Let's calculate the amount of work done by both of them working together in 1 minute. WORK = 1/5 + 1/15 Simplify, LCM of 5 and 15 = 15 So, 3/15 + 1/15 = 4/15Hence, working together Ted and Galen can mow the lawn in 15/4 or 3.75 minutes or 3 minutes and 45 seconds.
Know more about power mower here:
https://brainly.com/question/14490427
#SPJ11
Answer detailed please

Answers
Answer:
container A
Step-by-step explanation:
In Container A, we can plot the points (0,60) adn (2, 35)
The slope is :
\(m_A = \frac{y_2-y_1}{x_2-x_1} \\\\= \frac{35-60}{2-0} \\\\= \frac{-25}{2}\\ \\m_A = -12.5\\\)
For container B, the slope is:
\(m_B = \frac{y_2-y_1}{x_2-x_1} \\\\= \frac{32-54}{3-1} \\\\= \frac{-22}{2}\\ \\m_B = -11\\\)
The negative sign of the slope indicates the direction of the slope
\(|m_A| = 12.5\\\\|m_B| = 11\)
12.5 > 11
The slope of container A is steeper than container B
Therefore, the water is draining out of container A at a faster rate than container B
Which is the simplified form of the expression
3(7/5x+ 4) – 2( 3/2- 5/4)
Answers
Answer:
=42+115x
10x
Step-by-step explanation:
3(7/5x+ 4) – 2( 3/2- 5/4)
=21/5x+12-2(6/4-5/4)
=21/5x+12-2×1/4
=21/5x+12-1/2
=21/5x+24/2-1/2
=21/5x+23/2
=42/10x+115x/10x
=42+115x
10x
After obtaining two heads from two tosses of a coin, the probability of obtaining a head on the next toss is __________.
O 2/5
O 3/16
O 1/2
O 2/3
Answers
The probability of obtaining a head on the next toss of a coin after obtaining two heads from two tosses is still 1/2 or 50%.
This is because each coin toss is an independent event, and the outcome of one toss does not affect the outcome of another toss. Therefore, the fact that two heads have been obtained in the previous two tosses does not change the probability of obtaining a head on the next toss, which is always 1/2 or 0.5 for a fair coin.
What is probability?Probability is the likelihood of an event occurring. The values are between 0 and 1. The closer it is to 1, the greater the probability.
For more information about probability, visit:
brainly.com/question/24756209
#SPJ11
Graphs A and B are the result of combining two linear functions, f(x) and g(x). The functions were combined by addition to form h(x), and then by multiplication to form j(x). Graph A Graph B Which statements describe the graphs? Select two options. Graph B represents h(x). Graph B represents j(x). The y-intercepts of both f(x) and g(x) can be 3. The y-intercepts of f(x) and g(x) have opposite signs. The rate of change for both f(x) and g(x) must be negative.
Answers
Because I just took a yess
In the diagram of circle A shown below , chords CD snd EF intersect at G, and chords CE and FD and drawn
Which statements is not always true?
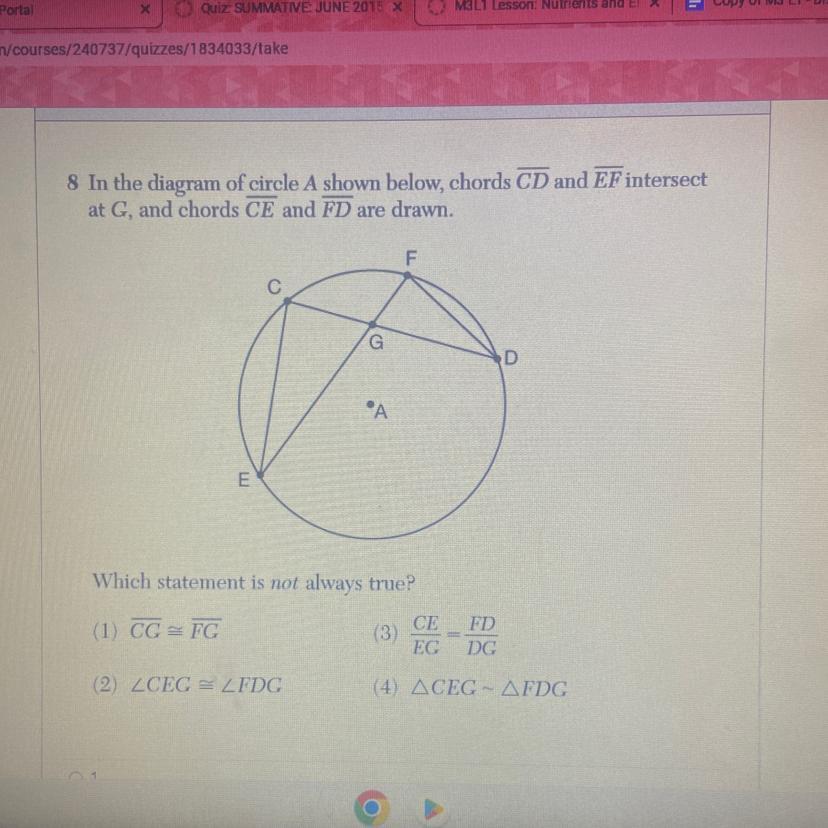
Answers
The incorrect statement about the intersecting triangles is A. CG ≅ FG.
Why is the statement CG ≅ FG incorrect about the intersecting triangles?With intersecting triangles, it is not always guaranteed that segments like CG and FG will be congruent. The lengths of CG and FG will depend on the specific configuration of the chords and their intersection point G.
However, CE/EG = FD/DG statement is TRUE. This is a consequence of the Intersecting Chords Theorem. When two chords intersect inside a circle, the products of their segments are equal.
Since ∠CEG ≅ ∠FDG intersect inside a circle, the corresponding intercepted arcs create equal angles at the intersection point. Therefore the statement is true.
ΔCEG ~ ΔFDG is also true because we know that the triangles share an angle and have proportional sides.
The answer above is in response to the full question below;
In the diagram of circle A shown below , chords CD and EF intersect at G, and chords CE and FD and drawn
Which statements is not always true?
a. CG ≅ FG
b. CE/EG = FD/ DG
c. ∠CEG ≅ FDG
d. ΔCEG ~ ΔFDG
Find more exercises on intersecting triangles;
https://brainly.com/question/28008595
#SPJ1
I need answer Immediately!!!!!!

Answers
Answer:
Step-by-step explanation:
https://www.numerade.com/questions/write-the-equation-for-the-graph-that-is-shown-check-your-book-to-see-graph-3/
Hope it helps you
Hen interpreting f (7, 31) = 4.78, p > 0.05, how many subjects were tested in this simple one-way anova?
Answers
39 subjects were tested in this simple one-way ANOVA.
The df for F distribution is (treatment df, error df)
Using given information
Treatment df = 7
Error df = 31
Total df= 7+31 = 38
Again, total df = N-1, N= number of subjects tested
Then, N-1 = 38
=> N= 39
One-way ANOVA is typically used when there is a single independent variable or factor and the goal is to see whether variation or different levels of that factor have a measurable effect on the dependent variable.
The t-test is a method of determining whether two populations are statistically different from each other, and ANOVA determines whether three or more populations are statistically different from each other.
For more information about one-way ANOVA,visit
brainly.com/question/24157862
#SPJ4
