Jayden need wood to enclose his garden he measures one side of his garden and finds it is 6 feetlong how many feet of wood does jayden need to enclose his garden
Answers
To enclose his garden, Jayden needs 24 feet of wood assuming his rectangular-shaped garden has sides of 6 feet each.
How much wood does Jayden need?Jayden needs wood to enclose his garden. He measured one side of his garden and found that it is 6 feet long.
To calculate how many feet of wood Jayden needs to enclose his garden, we need to know the length of all sides of the garden.
Assuming that the garden is rectangular in shape, we need to know the length of the other side as well.
Let's say the other side is also 6 feet long. In this case, we can calculate the total length of wood required by using the formula for the perimeter of a rectangle, which is:
Perimeter = 2 x (Length + Width)
Here, the length and width of the garden are both 6 feet.
So, we can substitute these values in the formula and get:
Perimeter = 2 x (6 + 6) = 2 x 12 = 24 feet
Therefore, Jayden needs 24 feet of wood to enclose his garden.
Learn more about wood
brainly.com/question/10967023
#SPJ11
Related Questions
Type the correct answer in the box.
In the figure, a square is inside another bigger square.
If a = 4 units and b = 3 units, the length of the diagonal of the outside square rounded to the nearest tenth is
units and the length of the diagonal of the inside square rounded to the nearest tenth is
units.

Answers
Answer:
For the outside square, the diagonal is 7√2, or about 9.9 units.
For the inside square, the diagonal is 5√2, or about 7.1 units.
use the kkt
Use the method of steepest ascent to approximate the solution to max z = -(x₁ - 3)² - (x₂ - 2)² s. t. (x₁, x₂) E R²
Answers
To approximate the solution and maximize the given objective function we need to find the steepest ascent direction and iteratively update the values of x₁ and x₂ to approach the maximum value of z.
The method of steepest ascent involves finding the direction that leads to the maximum increase in the objective function and updating the values of the decision variables accordingly. In this case, we aim to maximize the objective function z = -(x₁ - 3)² - (x₂ - 2)².
To find the steepest ascent direction, we can take the gradient of the objective function with respect to x₁ and x₂. The gradient represents the direction of the steepest increase in the objective function. In this case, the gradient is given by (∂z/∂x₁, ∂z/∂x₂) = (-2(x₁ - 3), -2(x₂ - 2)).
Starting with initial values for x₁ and x₂, we can update their values iteratively by adding a fraction of the gradient to each variable. The fraction determines the step size or learning rate and should be chosen carefully to ensure convergence to the maximum value of z.
By repeatedly updating the values of x₁ and x₂ in the direction of steepest ascent, we can approach the solution that maximizes the objective function z. The process continues until convergence is achieved or a predefined stopping criterion is met.
Learn more about fraction here:
https://brainly.com/question/10354322
#SPJ11
The acties director of the Community Center is planning a skaiing event for all the students at the local middle school. There are several skating rinks in the area, but the director does not know which one to use. Skate Fest charges a fee of $200 plus $3 per skater, while Roller Rama charges $5 per skater.
Answers
Skate Fest's event will cost 200 plus three times that amount. The price of the Roller Rama event can be expressed as 5x.
The mathematical statement 200 + 3x, where x represents the quantity of students attending the event, can be used to calculate the cost of Skate Fest. This amounts to the $200 set cost plus an extra $3 for each skater. The mathematical equation 5x, where x is the number of kids attending the event, can be used to indicate the cost of the Roller Rama event. This equates to $5 for each skater. The director can evaluate whether skating rink is more economical based on the amount of students attending the event by contrasting these two statements. An event is a planned and choreographed occurrence, such a social gathering or sporting competition. The three-day competition's cross-country portion was held here yesterday.
To know more about event here
https://brainly.com/question/24513174
#SPJ4
Given x || y.
∠6 and ∠8 are _________ angles.
complementary
corresponding
supplementary
vertical

Answers
Answer:
angle 6 and angle 8 are vertical angles
Step-by-step explanation:
The angles opposite to each other when two lines cross are called vertical angles. In this case, angle 6 and angle 8 are those angles.
what are two numbers that are greater than 14 but less than 15
Answers
Answer:
14.1, 14.2, 14.3, 14.4, 14.5, 14.6, 14.7, 14.8, 14.9
Step-by-step explanation:
decimals
Answer:
14.3 and 14.4 But there are also all of the decimals in between
Step-by-step explanation:
14.3 is greater than 14 but at the same time less than 15
What is zero divided by zero????? I NEED TO KNOW!!!!!!
Answers
Answer: Error
Step-by-step explanation: Its impossible to divide by zero.
Answer:
0
Explanation Anything divided by zero is zero
help???????????????????

Answers
Answer:
Please check the explanation.
Step-by-step explanation:
Part a)
Given
m∠ABD = (7q - 46)°m∠CBD = (3q + 6)°It is clear that m∠ABD and m∠CBD lie on a straight line.
Thus, the sum of m∠ABD and m∠CBD will be 180°.
Hence,
m∠ABD and m∠CBD are supplementary angles.
Part b)
As m∠ABD and m∠CBD are supplementary angles, so the sum of m∠ABD and m∠CBD will be 180°.
Thus,
m∠ABD + m∠CBD = 180°
substitute m∠ABD = (7q-46)° and m∠CBD = (3q + 6)°
(7q-46)° + (3q + 6)° = 180°
Part c)
Given the equation
(7q-46)° + (3q + 6)° = 180°
Combining the like terms
7q + 3q - 46 + 6 = 180
10q - 40 = 180
10q = 180 + 40
10q = 220
divide both sides by 10
10q/10 = 220/10
q = 22
Therefore, the value of q = 22
Part d)
As
m∠ABD = (7q-46)°
substituting q = 22
m∠ABD = 7(22) - 46
= 154 - 46
= 108°
also
m∠CBD = (3q + 6)°
substituting q = 22
m∠CBD = 3(22) + 6
= 66+6
= 72°
Therefore,
m∠ABD = 108°m∠CBD = 72°A cold drink initially at 35 f warms up to 42 f in min while sitting in a room of temperature 72f. how warm will the drink be if left out for 30 min?
Answers
\($$\begin{aligned}&T^{\prime}=-k(T-72) \quad T(0)=35 \text { (given) } \\&\frac{d T}{T-72}=-k d t-\left\{q^n(1)\right. \\&\text { Solphy } k g^n(1) \\&\ln (T-72)=0-k t+1 \\&T-72=e^{-k t+t} \\&T-72=e^{-k t} e^l \\&\text { let } e^r=C \\&T-72=C e^{-k t} \\&T=72+C e^{-k t} \\&T(t)=72+c e^{-k t}(2)\end{aligned}$$\)\($T(t)=72+c e$ Now at $t=Q \mathrm{~mm} \quad T=42$ given Now at $t=Q \min T=$$$\begin{aligned}&\text { yed: } 72+4 e^{-k t} \\&35=72+c e^{-k 0} \\&C=-37 \\&\text { at }+=2 \text { min } T=42 \\&\text { a gaim puting in \&qn } \\&42=72-3+e^{-2 k}\end{aligned}$$\)\($$\begin{array}{rl}-\frac{30}{37} & =e^{-2 k} \\e^{-2 k} & =\frac{30}{37} \\-2 k & =\ln \left(\frac{30}{37}\right) \\k & =0.1048 \\p 1 h y & m n \\T(t) & =72-37 e^{-0.1048+} \\T(15) & =72-37 e^{-0.1048 \times 15} \\T(15) & =72-37 \times 1 \\T(15) & =64.31 \\& =\end{array}$$\)
What is Fahrenheit?The unit is the degree Fahrenheit, represented by the sign °F. There are various accounts of how he initially defined his scale, but the initial paper suggests that the lower defining point, 0 °F, was established as the freezing temperature of a brine solution made from a combination of water, ice, and ammonium chloride (a salt). The other limit established was his best estimate of the average human body temperature, originally set at 90 °F, then 96 °F (about 2.6 °F less than the modern value due to He did, however, mention a midpoint at 32 °F, which would be the temperature of ice water.
To know more about Fahrenheit, visit;
https://brainly.com/question/516840
#SPJ4
If f(x)=ln(x+4+e^(-3x)), then f '(0) =
Answers
If derivative of \(f(x)=ln(x+4+e^{(-3x)})\), then f '(0) = -2/5.
What is derivative?
In calculus, the derivative of a function is a measure of how the function changes as its input changes. More specifically, the derivative of a function at a certain point is the instantaneous rate of change of the function at that point.
To find f'(0), we first need to find the derivative of f(x) with respect to x. Using the chain rule, we get:
\(f'(x) = 1 / (x+4+e^{(-3x)}) * (1 - 3e^{(-3x)})\)
Now we can find f'(0) by substituting the value x=0:
\(f'(0) = 1 / (0+4+e^{(-3(0))}) * (1 - 3e^{(-3(0))})\)
f'(0) = 1 / (4+1) * (1 - 3)
f'(0) = -2/5
Therefore, f'(0) = -2/5.
To learn more about derivative visit:
https://brainly.com/question/23819325
#SPJ4
3x+7+56=90 what is this
Answers
Answer:
X=9
Hope this helps! :)
What is 88% of %33.00
Answers
88/100 * 33/100
0.88*0.33
0.2904
29.04%
Select all correct answers. which values are part of the solution set based on the result of the inequality? -4x + 24 < -2x + 2 9.5 -10 11.5 15 10 -3
Answers
11.5 and 15 are the values that are part of the solution set of the inequality.
Inequality is defined as relationship between non-equal numbers or expressions. The solution of an inequality is the set of values that satisfies the given inequality.
To determine the solution set of the given inequality, isolate the variable to one side and simplify.
-4x + 24 < -2x + 2
-4x + 2x < -24 + 2
-2x < -22
22 < 2x
11 < x
Hence, the solution set of the given inequality is the set of numbers greater than 11. Among the given choices, 11.5 and 15 are both greater than 11.
Learn more about inequality here: https://brainly.com/question/13912022
#SPJ4
The population of City A starts with 200 people and grows by a factor of 1.05 each year.
The population of City B starts with 200 people and increases by 20 people each year.
1. Which city will have more people after 1 year? How do you know?
2. What type of equation is A?
3. What type of equation is B?
Answers
Answer:
1. City A
2. Exponential Growth
3. Linear
Step-by-step explanation:
The equation for exponential growth is f(x)=a(1+r/100)^x, where a is the initial growth/starting population, r is the growth rate, and x is the time intervals.
City A
f(x)=200(1+1.05/100)^x
Simplify:
f(x)=200(1.105)^x
City B
An increase in 20 people each year is NOT exponential but linear:
f(x)=20x+200
Now we plug in x for 1 to stand for 1 year and see which city has a greater number:
City A:
f(1)=200(1.105)^1
f(1)=200 x 1.105
f(1)=221
City B:
f(1)=20(1)+200
f(1)=20+200
f(1)=220
City A will have more people.
City A is an exponential function because there's a percent increase every year, and there will be more people every year because there are more people. This is kind of how compound interest also works
City B is a linear equation because a set number of people are added every year and doesn't change based on the amount of people already in it.
1. City B will have more population after 1 year.
In this case, we have been given of both the cities A and B with each year's growth factor and we have been told to find out, which city will have more population after 1 year. So to find out the comparison, first we need to find out the individual popoulation of both the cities after 1 year of interval.
So, population of City A after 1 year will be 200 * 1.05 = 210
Similarly, population of City B after 1 year will be 200 + 20 = 220
It is clear that City B has more population as compared to City A.
Therefore, after 1 year City B has more population.
2. equation for City A is Exponential Growth Equation.
Exponential growth is the growth which takes place when a particular quantity increases at a constant rate over a fixed time period. It is given in the form of \(P = P_{0} * (1 + r)^t\), where P is population, \(P_{0}\) is initial population, r is the growth rate, and t is time period.
3. equation for City B is Linear Equation.
Linear equation is a representation of a straight line when graphed on paper. It has constant coefficients and variables raised to power 1. It is given in the form of \(P = P_{0} + rt\), where P is population, \(P_{0}\) is initial population, r is the growth rate, and t is time period.
To study more about Exponential Growth Equation:
https://brainly.com/question/30690645
Find k so that the line through (2,-2) and (k, 1) is a. parallel to 5x + 6y = 12, b. perpendicular to 4x - 5y = -3 a. k= (Type an integer or a simplified fraction.) b. k= (Type an integer or a simplif
Answers
We have found that k= -5 so that the line through (2,-2) and (k,1) is parallel to 5x+6y=12 and k = -11/2 so that the line through (2,-2) and (k,1) is perpendicular to 4x-5y=-3.
a) We are given the equation of a line in the form 5x + 6y = 12.
To determine the slope of the line we will transform the equation into slope-intercept form which is y=mx+b.
5x + 6y = 12 ==> 6y = -5x + 12 ==> y = (-5/6)x + 2So the slope of this line is -5/6.
Since we are asked to find the line through (2, -2) and (k, 1) that is parallel to the line 5x + 6y = 12, the slope of this new line must also be -5/6. We can use the slope formula to determine k.
We have m=-5/6, and using the coordinates of the two points, we have:(1+2)/2 =
(-2-k)/2==> 3/2
= (-2-k)/2==> 3
= -2-k==>
k = -5
Therefore, k = -5, and the line through the two given points is parallel to the line 5x + 6y = 12. b) Again, we will determine the slope of the line with equation 4x - 5y = -3.4x - 5y = -3 ==> -5y = -4x - 3 ==> y = (4/5)x + 3/5The slope of this line is 4/5.
The slope of the line perpendicular to this line is the negative reciprocal of 4/5 which is -5/4. Using the slope formula with the two points we are given, we have:-
5/4 = (1+2)/2 - (-2-k)/2==> -5/4 = 3/2 + k/2==> k/2
= -5/4 - 3/2==> k/2 = -5/4 - 6/4==> k/2 = -11/4=
=> k = (-11/4) * 2==> k = -11/2
Therefore, k = -11/2, and the line through the two given points is perpendicular to the line 4x - 5y = -3.
We have found that k= -5 so that the line through (2,-2) and (k,1) is parallel to 5x+6y=12 and k = -11/2 so that the line through (2,-2) and (k,1) is perpendicular to 4x-5y=-3.
To know more about slope formula visit:
brainly.com/question/30619565
#SPJ11
a) Find the marginal probability mass function pX(x). Round the answers to two decimal places.
a.1) Px(0)
a.2) Px(1)
a.3) Px(2)
b) Find the marginal probability mass function pY(y). Round the answers to two decimal places.
b.1) Py(0)
b.2) Py(1)
b.3) Py(2)
c) Find µX
d) Find μY. Round the answer to two decimal places.
e) Find σX.
f) Find σY.
g) Find Cov(X, Y).
h) Find rhoX,Y .
Answers
The Cov(X,Y) = E(XY) - E(X)E(Y) = 1.26 - 0.76(1.70) = 0.02h) Find ρX,Y.To find the correlation coefficient of X and Y, we use the formula ρX,Y = Cov(X,Y) / (σXσY). We already calculated Cov(X,Y) to be 0.02. Now we need to calculate σX and σY. We calculated σX to be 0.638. We could not calculate σY because the variance was negative. Therefore, we cannot find the correlation coefficient of X and Y.
Find the marginal probability mass function pX(x). Round the answers to two decimal places.a.1) Px(0)a.2) Px(1)a.3) Px(2)We can use the following formula to find the marginal probability mass function: Px(x) = Σy P(x, y) where Σy is the sum of all the values of y for each value of x.
The table shows the joint probability mass function of the random variables X and Y.X/Y|0 |1 |2 |P(X=x)0 |0.12 |0.16 |0.280.6 |1 |0.18 |0.14 |0.320.64 |2 |0.10 |0.12 |0.22Let's now use the formula to find Px(0):Px(0) = Σy P(0, y) = P(0,0) + P(0,1) + P(0,2) = 0.12 + 0.16 + 0.28 = 0.56Now we'll find Px(1):Px(1) = Σy P(1, y) = P(1,0) + P(1,1) + P(1,2) = 0.18 + 0.14 = 0.32Lastly, we'll find Px(2):Px(2) = Σy P(2, y) = P(2,0) + P(2,1) + P(2,2) = 0.10 + 0.12 = 0.22b)
Find the marginal probability mass function pY(y). Round the answers to two decimal places.b.1) Py(0)b.2) Py(1)b.3) Py(2)We can use the following formula to find the marginal probability mass function: Py(y) = Σx P(x, y) where Σx is the sum of all the values of x for each value of y. The table shows the joint probability mass function of the random variables X and Y.X/Y|0 |1 |2 |P(X=x)0 |0.12 |0.16 |0.280.6 |1 |0.18 |0.14 |0.320.64 |2 |0.10 |0.12 |0.22
Let's now use the formula to find Py(0):Py(0) = Σx P(x, 0) = P(0,0) + P(1,0) + P(2,0) = 0.12 + 0.18 + 0.10 = 0.40Now we'll find Py(1):Py(1) = Σx P(x, 1) = P(0,1) + P(1,1) + P(2,1) = 0.16 + 0.14 + 0.12 = 0.42Lastly, we'll find Py(2):Py(2) = Σx P(x, 2) = P(0,2) + P(1,2) + P(2,2) = 0.28 + 0.14 + 0.22 = 0.64c) Find µXTo find µX, we use the formula µX = E(X) = Σx xP(X = x).
We can calculate the expected value of X by using the marginal probability mass function Px(x) that we previously calculated. The formula is: E(X) = Σx xPx(x) = 0(0.56) + 1(0.32) + 2(0.22) = 0 + 0.32 + 0.44 = 0.76Therefore, µX = 0.76d) Find μY.
Round the answer to two decimal places.To find µY, we use the formula µY = E(Y) = Σy yP(Y = y). We can calculate the expected value of Y by using the marginal probability mass function Py(y) that we previously calculated. The formula is: E(Y) = Σy yPy(y) = 0(0.40) + 1(0.42) + 2(0.64) = 0 + 0.42 + 1.28 = 1.70Therefore, µY = 1.70e) Find σX.To find the standard deviation of X, we can use the formula σX = sqrt(V(X)) where V(X) is the variance of X. To find the variance of X, we use the formula V(X) = E(X²) - [E(X)]². We already calculated E(X) to be 0.76. Now we need to calculate E(X²):E(X²) = Σx x²P(X = x) = 0²(0.56) + 1²(0.32) + 2²(0.22) = 0 + 0.32 + 0.88 = 1.20
Therefore, V(X) = E(X²) - [E(X)]² = 1.20 - 0.76² = 0.4064σX = sqrt(V(X)) = sqrt(0.4064) = 0.638f) Find σY.To find the standard deviation of Y, we can use the formula σY = sqrt(V(Y)) where V(Y) is the variance of Y. To find the variance of Y, we use the formula V(Y) = E(Y²) - [E(Y)]².
We already calculated E(Y) to be 1.70. Now we need to calculate E(Y²):E(Y²) = Σy y²P(Y = y) = 0²(0.40) + 1²(0.42) + 2²(0.64) = 0 + 0.42 + 1.28 = 1.70Therefore, V(Y) = E(Y²) - [E(Y)]² = 1.70 - 1.70² = -0.29σY = sqrt(V(Y)) = sqrt(-0.29)This is an invalid result, since the variance cannot be negative. Therefore, there may be an error in the calculations or in the values provided in the table.
We cannot find the standard deviation of Y.g) Find Cov(X, Y).To find the covariance of X and Y, we use the formula Cov(X,Y) = E(XY) - E(X)E(Y). We already calculated E(X) and E(Y) to be 0.76 and 1.70 respectively. Now we need to calculate E(XY):E(XY) = Σx Σy xyP(X = x, Y = y) = 0(0)(0.12) + 0(1)(0.16) + 0(2)(0.28) + 1(0)(0.18) + 1(1)(0.14) + 1(2)(0.00) + 2(0)(0.10) + 2(1)(0.12) + 2(2)(0.22) = 0 + 0 + 0 + 0 + 0.14 + 0 + 0 + 0.24 + 0.88 = 1.26
Therefore, Cov(X,Y) = E(XY) - E(X)E(Y) = 1.26 - 0.76(1.70) = 0.02h) Find ρX,Y.To find the correlation coefficient of X and Y, we use the formula ρX,Y = Cov(X,Y) / (σXσY). We already calculated Cov(X,Y) to be 0.02. Now we need to calculate σX and σY. We calculated σX to be 0.638. We could not calculate σY because the variance was negative. Therefore, we cannot find the correlation coefficient of X and Y.
Learn more about Correlation coefficient
brainly.com/question/27226153
#SPJ11
Select ALL the expressions that are equivalent to (x^2)(square root of x).
Answers
Answer:
x^(2.5) ("x to the power 5/2")
Step-by-step explanation:
(x^2)(√x) can also be written as x·x·x^(1/2). We just add the exponents together: (x^2)(√x) = x^1·x^1·x^(1/2) = x^(2.5) ("x to the power 5/2").
Next time, please share the answer choices.
In 2014, a survey stated that 51% of 650 randomly sampled North Carolina residents planned to set off fireworks on July 4th. a) Determine the margin of error for the 95% confidence interval for the proportion of North Carolina residents that plan to set off fireworks. Give your answer to three decimal places. Margin of Error = _____% b) How many randomly sampled residents do we need to survey if we want the 95% margin of error to be less than 3%? Sample size > _____ People
Answers
To find the required sample size for a margin of error less than 3%, we can rearrange the formula for the margin of error:
\(n = (Z^2 * p * (1 - p)) / (E^2)\)
Here, Z represents the critical value, p is the estimated proportion (0.51), and E is the desired margin of error (0.03)
To determine the margin of error for the 95% confidence interval, we need to use the formula:
Margin of Error = Critical value * Standard error
The critical value for a 95% confidence level can be obtained from the standard normal distribution table, which corresponds to 1.96. The standard error can be calculated using the following formula:
Standard error = \(\sqrt{(p * (1 - p) / n)}\)
Given that the proportion of North Carolina residents planning to set off fireworks is estimated to be 51% (0.51) based on the survey, we can substitute the values into the formula. However, the sample size (n) is not provided in the question, so we need to determine it in the next part.
To find the required sample size for a margin of error less than 3%, we can rearrange the formula for the margin of error:
\(n = (Z^2 * p * (1 - p)) / (E^2)\)
Here, Z represents the critical value, p is the estimated proportion (0.51), and E is the desired margin of error (0.03). Substituting these values into the formula, we can solve for the required sample size.
Learn more about standard normal distribution here:https://brainly.com/question/15103234
#SPJ11
for a two-force body in equilibrium, identify the true statements.
Answers
For a two-force body in equilibrium, the following are the true statements:The body must have no acceleration. This means that the net force acting on it must be zero. Therefore, the two forces must be equal in magnitude but opposite in direction.
A force is a vector quantity with both magnitude and direction. Since two forces are acting on the same body in opposite directions, they must be of equal magnitude and must cancel each other out to keep the body in equilibrium.
For example, if one force is 10 N to the right, the other force must be 10 N to the left. For the two-force body in equilibrium, the point of application of each force must be in line with the other
. The point of application of each force must be on the same line of action for the two forces to be in equilibrium. Otherwise, the body will experience a torque or a moment that can cause it to rotate around its center of mass or axis.
For example, if one force is applied at the top of the body and the other at the bottom, the body will not be in equilibrium and will tend to rotate.
A two-force body in equilibrium must be rigid. This means that the body must be able to maintain its shape and size under the action of the two forces. If the body deforms or changes shape, it will not be in equilibrium.
For example, if two forces are acting on a rubber ball, the ball will deform and change shape under the forces, so it will not be in equilibrium.
Therefore, a two-force body in equilibrium must be rigid, such as a metal or wooden block. Thus, a two-force body in equilibrium must have no acceleration, the two forces must be equal in magnitude but opposite in direction, the point of application of each force must be in line with the other, and the body must be rigid. These are the true statements for a two-force body in equilibrium.
Learn more about equilibrium from:
https://brainly.com/question/517289
#SPJ11
the radius of the earth - the distance from surface to core - is 6,370 kilometers. the planet neptune is 24,620 kilometers. if a scale model of the earth is drawn with a radius of 2.5 centimeters, how large would a scale model of neptune have to be drawn? group of answer choices 9848 cm 9.7 cm 2548 cm 0.02548 cm 3.86 cm
Answers
We may build up a proportion and solve for the scale model radius of Neptune using the ratio between the radii of the two planets and the known scale model radius of the Earth. The scale model of Neptune that is produced has a radius of around 9.7 cm.
We may take advantage of the fact that the ratio between the two planets' radii and the ratio between their respective scale model radii is the same. Let's name the Neptune scale model radius "r" Then, we may set up the ratio shown below:
Neptune's radius is equal to the product of Earth's radius and its scale model.
With the provided values, we may simplify and obtain:
24620 km / 6370 km equals 2.5 cm / r
We obtain the following when solving for "r":
r = (24620 km * 2.5 cm) / (6370 km)
r ≈ 9.7 cm
Therefore, a scale model of Neptune would have to be drawn with a radius of approximately 9.7 cm.
Learn more about scale models here:
https://brainly.com/question/17581605
#SPJ4
A movie rental store charges a membership fee of $10.00 plus $1.50 per movie rented. What is a possible domain that shows the cost to a member of renting movies? (1 point)
The domain is all integers.
The domain is all even integers.
The domain is all integers 0 or greater.
The domain is all integers 10 or greater.
Answers
I recommed for the people tat are seraching up this question to not read the comments
Can someone help me with this. Will Mark brainliest.
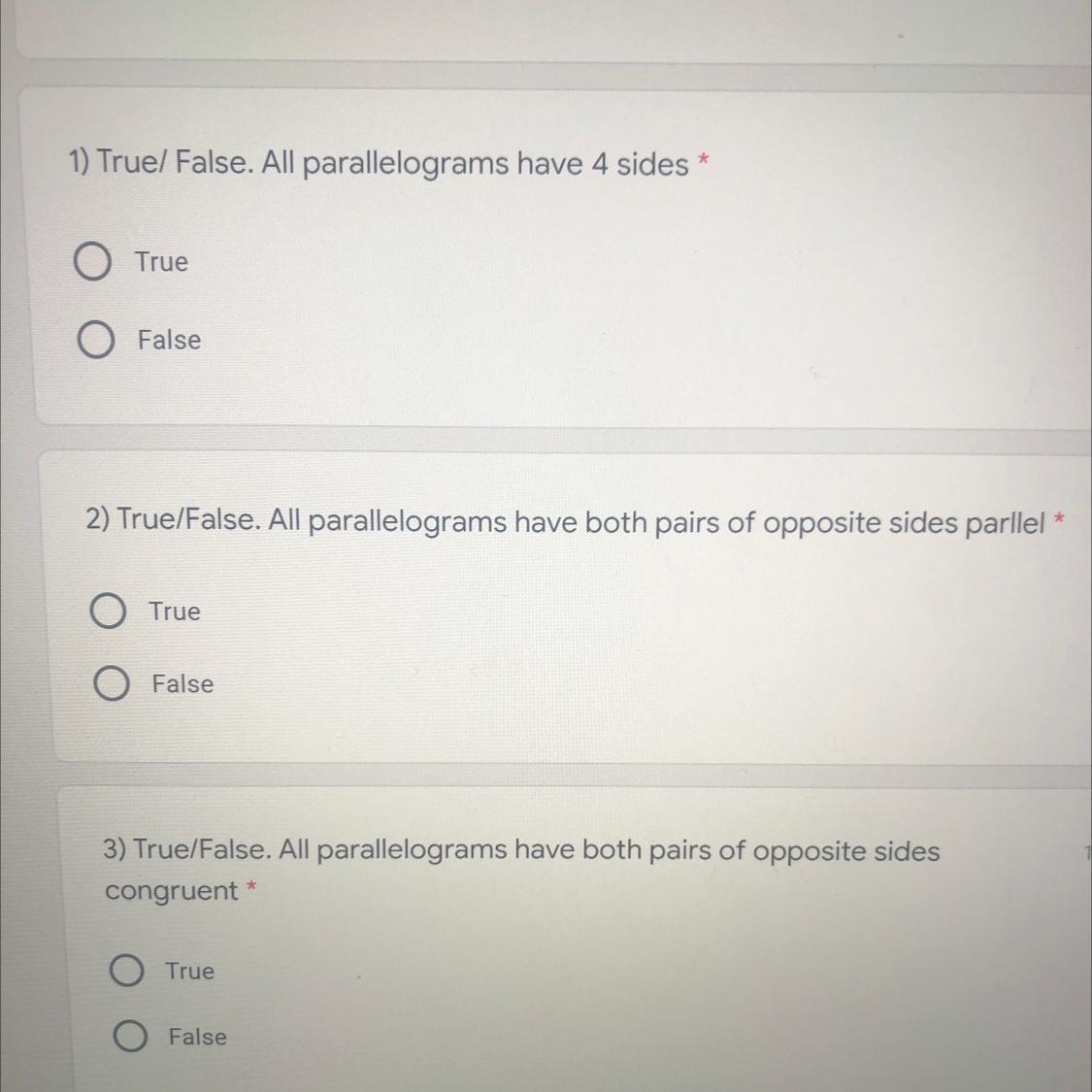
Answers
Answer:
1. True
2. True
3. True
A regression analysis resulted in the following fitted regression line y = 35 − 1.2x
In addition, the total sum of squares was SSY = 2758, and the error sum of squares was SSE = 652.
[a] Compute r 2 , the coefficient of determination. Round your answer to four decimal places.
[b] Compute r, the correlation coefficient. Round your answer to four decimal places.
[c] Compute the predicted mean of Y when X = 10
Answers
The regression analysis yielded a fitted line, y = 35 - 1.2x, with a coefficient of determination of 0.7632, a correlation coefficient of 0.8740, and a predicted mean of Y = 23 when X = 10.
To compute the coefficient of determination (r²), the correlation coefficient (r), and the predicted mean of Y when X = 10, we can use the given regression line y = 35 - 1.2x and the formulas related to regression analysis.
The coefficient of determination (r²) represents the proportion of the total variation in the dependent variable (Y) that can be explained by the independent variable (X). It is calculated by dividing the explained sum of squares (SSR) by the total sum of squares (SSY).
[a] To compute r²:
SSR = SSY - SSE
SSR = 2758 - 652 = 2106
r² = SSR / SSY
r² = 2106 / 2758 = 0.7632
Therefore, the coefficient of determination (r²) is 0.7632 (rounded to four decimal places).
[b] To compute the correlation coefficient (r):
We can use the formula:
r = √(r²)
r = √(0.7632) = 0.8740
Therefore, the correlation coefficient (r) is 0.8740 (rounded to four decimal places).
[c] To compute the predicted mean of Y when X = 10:
We can substitute the value of X = 10 into the regression line equation y = 35 - 1.2x:
y = 35 - 1.2(10)
y = 35 - 12
y = 23
Therefore, the predicted mean of Y when X = 10 is 23.
To know more about regression analysis,
https://brainly.com/question/31985268
#SPJ11
You owe your best friend $50 for paying for your meal when you
went out to dinner with some friends. You can only spare $5
each week from your check from your part time job and can
right now give him $7 in your wallet. How long will it take you to
owe him $0.
Answers
Answer:
9 weeks.
Step-by-step explanation:
It will take 9 weeks because $50-$7 is $43.
It will take 9 weeks because you can't pay $40, you have to pay $45.
assume z is a standard normal random variable. then p(1.41 < z < 2.85) equals . a. .4772 b. .3413 c. .8285 d. .0771
Answers
The value of P(1.41 < Z < 2.85) is 0.0771.
Hence, the correct answer is d.
A normally distributed random variable with mean μ= 0 and standard deviation σ= 1 is referred to as a standard normal random variable. The letter Z will always be used to represent it.
Because the Standard Normal Distribution is a probability distribution, the area under the curve between two points indicates the likelihood that variables will take on a range of values.
The whole area under the curve is one, or one hundred percent.
The mean and variance of a normal distribution are governed by two factors.
A standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1.
The probability that a standard normal random variable Z is between 1.41 and 2.85 can be found using a standard normal table with a standard normal cumulative distribution function.
The answer is approximate:
P(1.41 < Z < 2.85)
= P(Z < 2.85) - P(Z < 1.41)
= 0.9927 - 0.9185
= 0.0742
For more questions on Standard Normal Distribution
https://brainly.com/question/4079902
#SPJ4
Please help!!!!!!!!!

Answers
Answer:
hopes it's helps
Step-by-step explanation:
I got 20 blocks for my answer
Answer:
20 blocks from the bottom
Step-by-step explanation:
red - 3. 6. 9. 12. 18. 21. 24. 27.
green - 5. 10. 20. 25.
yellow - 15. 30.
the 20th block is the third painted green block from the bottom
Suppose you invest in shares of Merck at $40 per share and shares of Yahoo at $25 per share. If the price of Merck increases to $45 and the price of Yahoo decreases to $22 per share, what is the return on your portfolio
Answers
The return on portfolio is 4.11%.
The initial investment
Investment in Merck = Number of shares of Merck × Price per share Investment in Merck = 120 shares × $40 per share
Investment in Merck = $4,800
Investment in Yahoo = Number of shares of Yahoo × Price per share Investment in Yahoo = 100 shares × $25 per share
Investment in Yahoo = $2,500
Now, let's calculate the current value of the portfolio
Current value of Merck = Number of shares of Merck × Current price per share
Current value of Merck = 120 shares × $45 per share
Current value of Merck = $5,400
Current value of Yahoo = Number of shares of Yahoo × Current price per share
Current value of Yahoo = 100 shares × $22 per share Current value of Yahoo = $2,200
Current value of the portfolio = Current value of Merck + Current value of Yahoo
Current value of the portfolio = $5,400 + $2,200 Current value of the portfolio = $7,600
To calculate the return on the portfolio, we need to subtract the initial investment from the current value of the portfolio and divide it by the initial investment
Return on portfolio = (Current value of the portfolio - Initial investment) / Initial investment
Return on portfolio = ($7,600 - ($4,800 + $2,500)) / ($4,800 + $2,500)
Return on portfolio = ($7,600 - $7,300) / $7,300
Return on portfolio = $300 / $7,300
Return on portfolio ≈ 0.0411 or 4.11%
Therefore, the return on your portfolio is approximately 4.11%.
To know more about return click here:
https://brainly.com/question/32133392
#SPJ4
The question is incomplete the complete question is :

1. Differentiate the function f(x) = ln (81 sin^2 (x)) f’(x) 2. Differentiate the function P(t) = in ( √t2 + 9) p' (t) 3. if x2 + y2 + z2 = 9, dx/dt = B, and dy/dt = 4, find dz/dt when (x,y,z) = (2,2,1)
dz/dt =
Answers
First you will get 4dz
Trigonometric Ratios

Answers
Answer:
Sis I can't see
Step-by-step explanation:
.
.
.
.
.
Bnnn t is a great place to
solve for x
plsss. & then solve for y

Answers
Answer:
x=22, y=35
Step-by-step explanation:
since this is an isosceles triangle, 3x-11 = 2x+11. so x=22
since this is a triangle 3x-11 + 2x+11 + 2y = 180. plug in x and simplify to get 2y+110=180, so 2y=70 and y=35
There are 9 gallons of distilled water in the science supplies.
If 16 students each use an equal amount of the distilled water and there is 1 gal left in the supplies, how
much will each student get?
Each student will get
gal of distilled water.
how much will each student get?
Answers
Answer:
Each student will get a half a gallon of distilled water
Step-by-step explanation: