Jessica records the number of winners at the dunk-a-teacher booth at the town fair as shown in the table. if there are 750 contestants on monday, how many should jessica expect to dunk a teacher? enter your answer in the box.
Answers
If there are 750 contestants on Monday, Jessica should expect around 75 of them to dunk a teacher.
Based on the table provided, we can see that the percentage of winners at the dunk-a-teacher booth varies from day to day.
On Monday, 10% of contestants were able to dunk a teacher.
Therefore, if there are 750 contestants on Monday, Jessica should expect around 75 of them to dunk a teacher.
This is calculated by multiplying 750 by 0.10, which gives us 75. It's important to note that this is just an estimation, as the actual number of winners may be slightly higher or lower than 75.
However, this gives Jessica a rough idea of what to expect at the booth on Monday.
Learn more about simulation at
https://brainly.com/question/16359096
#SPJ11
Related Questions
What percent of the zones shall be tested at the outlet most remote from the source to verify the piping particulate test
Answers
The specific percentage of zones to be tested can range from 10% to 100%, depending on various factors. Higher percentages are typically recommended for critical systems or when stricter quality control is required.
To determine the percentage of zones that should be tested at the outlet most remote from the source, several factors need to be considered, such as the size of the system, the level of confidence desired, and any relevant industry standards or guidelines.
Typically, a common approach is to select a representative sample of zones that are distributed throughout the system. This sample should include zones that are farthest from the source to ensure comprehensive testing. The number of zones to be tested will depend on the size of the system and the level of confidence desired.
Learn more about number here:
https://brainly.com/question/3589540
#SPJ11
what is the term for the value that occurs most often in a series of numbers?
Answers
The term for the value that occurs most often in a series of numbers is called the mode.
The mode is one of the three main measures of central tendency, along with the mean and the median. It is a useful descriptive statistic that can provide insights into the characteristics of a dataset.
To find the mode of a set of data, you first need to arrange the data in order, either in increasing or decreasing order. Then, you simply identify the most frequent data point, which is the mode. In some cases, there may be more than one mode if multiple data points occur with the same maximum frequency.
The mode is particularly useful when dealing with categorical or nominal data, where there are distinct categories or values that cannot be ordered in a meaningful way. For example, the mode can help identify the most popular color among a group of people or the most common type of car on a given street. It can also be used for continuous data, although it may be less useful in this case than the mean or median.
For such more questions on value
https://brainly.com/question/843074
#SPJ8
let x = {−1, 0, 1} and a = (x) and define a relation r on a as follows: for all sets s and t in (x), s r t ⇔ the sum of the elements in s equals the sum of the elements in t.
Answers
The relation r defined on a is an equivalence relation, as it is reflexive, symmetric, and transitive.
Given x = {−1, 0, 1} and a = (x), where a is the set of all subsets of x. We define a relation r on a as follows:
For all sets s and t in a, s r t ⇔ the sum of the elements in s equals the sum of the elements in t.
To understand this relation, let's consider an example. Suppose s = {−1, 1} and t = {0, 1}. The sum of the elements in s is −1 + 1 = 0, and the sum of the elements in t is 0 + 1 = 1. Since the sum of the elements in s is not equal to the sum of the elements in t, s is not related to t under r.
Now, let's consider another example. Suppose s = {−1, 0, 1} and t = {−1, 1}. The sum of the elements in s is −1 + 0 + 1 = 0, and the sum of the elements in t is −1 + 1 = 0. Since the sum of the elements in s is equal to the sum of the elements in t, s is related to t under r.
We can also observe that the relation r is reflexive, symmetric, and transitive.
Reflexive: For any set s in a, the sum of the elements in s equals the sum of the elements in s. Therefore, s r s for all s in a.
Symmetric: If s r t for some sets s and t in a, then the sum of the elements in s equals the sum of the elements in t. But since addition is commutative, the sum of the elements in t also equals the sum of the elements in s. Therefore, t r s as well.
Transitive: If s r t and t r u for some sets s, t, and u in a, then the sum of the elements in s equals the sum of the elements in t, and the sum of the elements in t equals the sum of the elements in u. Therefore, the sum of the elements in s equals the sum of the elements in u, and hence, s r u.
Learn more about “ equivalence relation “ visit here;
https://brainly.com/question/14307463
#SPJ4
Complete the sequence,
13, 14, 27, 41,
Answers
Answer:
68
Step-by-step explanation:
We can see that the nth term would be the sum of the previous two terms. Continuing this would result in 68.
State the property that justifies each step.
13. Simplify: 6a +(8b+2a)
a. 6a +(8b+2a) = 6a+(2a+8b)
b. = (6a +2a) +8b
c. =(6+2)a +8b
Answers
Answer:
a. Using the commutative property of addition:
6a + (8b + 2a) = 6a + (2a + 8b)
b. Using the associative property of addition:
6a + (2a + 8b) = (6a + 2a) + 8b
c. Using the distributive property of multiplication over addition:
(6a + 2a) + 8b = (6 + 2)a + 8b
Jeremiah is creating a playlist that has only one song from each of his favorite genres. The following table shows his favorite genres and the number of songs on his MP3 player for each genre.
Answers
Answer:
Step-by-step explanation:
well i just dont know whats going on but just times the number of songs times the Genre.
Answer:
448
Step-by-step explanation:
just because
The expression 53(1+x) represents the total cost of a meal including the tip.
Answers
Answer:
53 + 53x
Step-by-step explanation:
Multiply each term in the parentheses by 53 and you get 53 + 53x
I hope that helps!!
Please help need answer soon!!!
A player drops a ball at the starting point. Is this game fair?

Answers
The game is fair, as the probability of winning is the same as the probability of losing.
How to calculate a probability?The parameters that are needed to calculate a probability are given as follows:
Number of desired outcomes in the context of a problem/experiment.Number of total outcomes in the context of a problem/experiment.A probability is then calculated as the division of the number of desired outcomes by the number of total outcomes.
A game is classified as fair if the probability of winning is the same as the probability of losing.
Of the 16 outcomes in this problem, we have that:
8 result in loss.8 result in win.Hence the probabilities are given as follows:
P(loss) = 8/16 = 1/2.P(win) = 8/16 = 1/2.Equal probabilities mean that the game is in fact fair.
Learn more about the concept of probability at brainly.com/question/24756209
#SPJ1
Answer:
The game is fair, as the probability of winning is the same as the probability of losing.
Which list of numbers contains ONLY integers?
π, 32, 7π, 32, 7
5,0,−35 comma 0 comma negative 3
3.2,0,−23 point 2 comma 0 comma negative 2
−30−−√, −85, − 6π
Answers
The list of numbers that contains Only integers is 5,0,−35 comma 0 comma negative 3.
What is an integer?An integers serves as the numbers that have no decimal or fractional part .
It should be noted that these numbers could contain negative and positive numbers, as well as zero.
The types of integers are:
Zero (0) Positive Integers (Natural numbers) Negative Integers (Additive inverse of Natural Numbers)Therefore, the list of numbers that contains Only integers is 5,0,−35 comma 0 comma negative 3.
Read more about integers ;
https://brainly.com/question/794810
#SPJ1
samantha wants too pour 3 gallons of water into cups. How many cups will be used?
Answers
Answer:
There are 48 cups in 3 gallons
Answer:
I believe 48 cups would be the answer
suppose you are interested in investigating factors that affect the prevalence of tuberculosis among intravenous drug users. in a group of 97 individuals who admit to sharing needles, 24.7% had positive tuberculin skin test results; among 161 drug users who deny sharing needles, 17.4% had positive test results [246]. assuming that the population proportions of positive skin test results are in fact equal, estimate their common value p. test the null hypothesis that the proportions of intravenous drug users who have positive tuberculin skin test results are identical for those who share needles and those who do not. what is the probability distribution of the test statistic? what is the p-value? what do you conclude? construct a 95% confidence interval for the true difference in proportions.
Answers
a. The probability distribution of the test statistic is approximately a standard normal distribution.
b. The p-value for the test of factors that affect the prevalence of tuberculosis among intravenous drug users is 0.0202.
c. We can conclude that there is a statistically significant difference between the two groups in terms of their proportions of positive skin test results.
d. The 95% confidence interval does not contain zero, so there is a statistically significant difference between the two groups in terms of their proportions of positive skin test results.
To estimate the common value of p assuming that the population proportions of positive skin test results are equal, we can compute the pooled proportion:
p-hat = (x1 + x2) / (n1 + n2)
= (24.7 + 17.4) / (97 + 161)
= 0.195
where x1 and x2 are the number of individuals with positive skin test results in the two groups, and n1 and n2 are the sample sizes.
a. To test the null hypothesis that the proportions of intravenous drug users who have positive tuberculin skin test results are identical for those who share needles and those who do not, we can use a two-sample z-test for proportions. The test statistic is:
z = (p1 - p2) / sqrt(phat * (1 - phat) * (1/n1 + 1/n2))
where p1 and p2 are the sample proportions, phat is the pooled proportion, and n1 and n2 are the sample sizes.
Plugging in the values, we get:
z = (0.247 - 0.174) / sqrt(0.195 * (1 - 0.195) * (1/97 + 1/161))
= 2.05
The probability distribution of the test statistic is approximately a standard normal distribution, since the sample sizes are large enough (both n1 and n2 are greater than 30).
b. The p-value for the test is the probability of observing a z-value of 2.05 or more extreme under the null hypothesis. From a standard normal distribution table or calculator, we find that the p-value is approximately 0.0202 (or 0.0404 for a two-tailed test).
Since the p-value is less than the significance level of 0.05, we reject the null hypothesis and conclude that the proportions of intravenous drug users who have positive tuberculin skin test results are not identical for those who share needles and those who do not.
c. To construct a 95% confidence interval for the true difference in proportions, we can use the formula:
(p1 - p2) ± z* sqrt(phat * (1 - phat) * (1/n1 + 1/n2))
where z is the critical value for a 95% confidence interval from a standard normal distribution (z = 1.96).
Plugging in the values, we get:
(0.247 - 0.174) ± 1.96 * sqrt(0.195 * (1 - 0.195) * (1/97 + 1/161))
= 0.073 ± 0.090
Therefore, we can be 95% confident that the true difference in proportions of intravenous drug users who have positive tuberculin skin test results between those who share needles and those who do not is between 0.073 and -0.073 (which can be written as an absolute value of 0.073).
d. We can infer that there is a statistically significant difference between the two groups in terms of the proportions of positive skin test results because the interval does not contain zero.
Learn more about hypothesis at https://brainly.com/question/21416205
#SPJ11
PLEASE HELP ME
7. What is the Range?
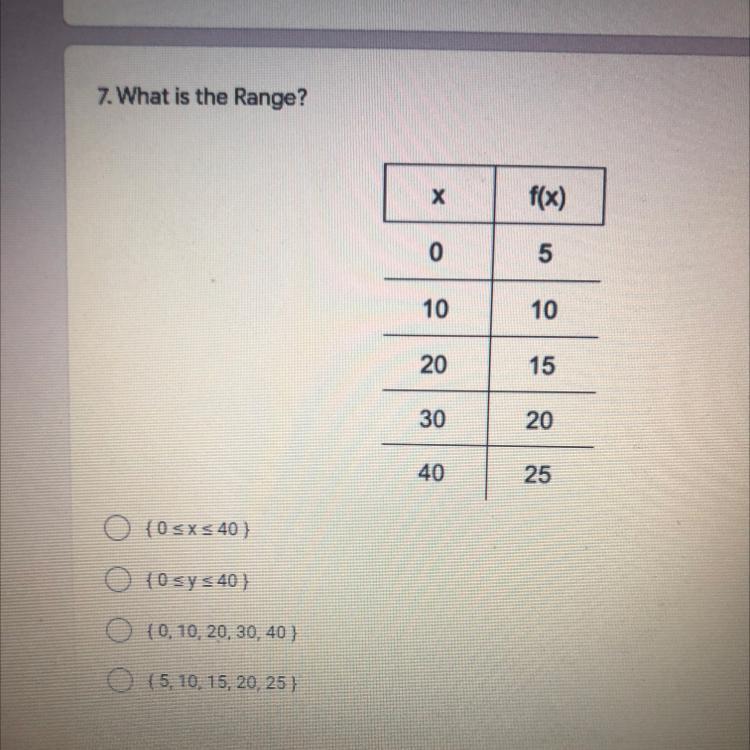
Answers
Answer:
the last one
Step-by-step explanation:
How does y=5x and y=5x-4 are related
Answers
These two equations have the same slope, slope = 5.
They have different intercepts (the origin (0,0) and (0, -4)).
These lines are parallel.
Select the best answer regarding the effects of Carbon monoxide: a. The affinity between CO and hemoglobin is about the same as oxygen. b. The central chemoreceptors will detect the reduction in oxygen delivered to the cells and will increase their firing rate. c. CO results in less oxygen loading hemoglobin but unloading is not changed. d. A small amount of CO in the air will not reduce arterial PO2 levels enough to be sensed by the peripheral chemoreceptors.
Answers
The best answer regarding the effects of carbon monoxide is option c, CO results in less oxygen loading hemoglobin but unloading is not changed.
Carbon monoxide binds up more tightly to the hemoglobin as compared to the oxygen molecules. This reduces the oxygen-carrying capacity of the blood and results in less oxygen loading onto hemoglobin.
However, once oxygen is already bound to hemoglobin, CO does not significantly affect its release or unloading. Therefore, option c is the most accurate statement among the given choices.
To know more about Carbon monoxide in blood, visit,
https://brainly.com/question/29233528
#SPJ4
how do you rewrite y=3x-4 using function notation
Answers
Answer:
f(x)=3x-4
Step-by-step explanation:
just replace the y with f(x)
Let T be a normal operator on a finite-dimensional complex inner product space V. Use the spectral decomposition T = 1171 + ... + dette to prove: (a) If T" is the zero map for some n e N, then T is the zero map. (b) U EL(V) commutes with T if and only if U commutes with each aj. (c) There exists a normal U E L(V) such that U2=T. (d) T is invertible if and only if ; 70 for all j. (e) T is a projection if and only if 1; = 0 or 1 for all j. (f) T = -T* if and only if X; is imaginary.
Answers
For T to be a normal operator on a finite-dimensional complex inner product space V,
(a) If Tⁿ is the zero map, then T is the zero map.
(b) U commutes with T if and only if U commutes with each eigenprojection of T.
(c) There exists a normal U such that U² = T.
(d) T is invertible if and only if lambda_j is nonzero for all eigenvalues λ_j of T.
(e) T is a projection if and only if lambda_j is either 0 or 1 for all eigenvalues λ_j of T.
(f) T = -T* if and only if each eigenvalue of T is imaginary.
(a) If Tⁿ = 0 for some n ∈ ℕ, then the characteristic polynomial of T is p_T(x) = xⁿ. But by the spectral decomposition, the characteristic polynomial of T is given by p_T(x) = (x - λ₁)(d₁) × ... × (x - λ_k)(d_k), where λ₁, ..., λ_k are the distinct eigenvalues of T and d₁, ..., d_k are the dimensions of the corresponding eigenspaces. Since T is normal, the eigenspaces are orthogonal and hence the dimensions add up to the dimension of V. Thus we must have n = dim(V), which implies that T is the zero map.
(b) Let U be a linear operator on V that commutes with T. By the spectral decomposition, we can write T = λ₁P₁ + ... + λ_kP_k, where P₁, ..., P_k are orthogonal projections onto the eigenspaces of T. Since U commutes with T, we have U(P_i(v)) = P_i(U(v)) for any eigenvector v of T. It follows that U commutes with each P_i. Conversely, suppose U commutes with each P_i. Then we have U(T(v)) = U(λ_i P_i(v)) = λ_i U(P_i(v)) = λ_i P_i(U(v)) = T(U(v)) for any eigenvector v of T. Since the eigenvectors span V, this implies that U commutes with T.
(c) Let T = λ₁P₁ + ... + λ_kP_k be the spectral decomposition of T. Define U = λ₁(1/2)P₁ + ... + λ_k(1/2)P_k. Since T is normal, the eigenspaces are orthogonal and hence the projections P₁, ..., P_k are also orthogonal. It follows that U is also an orthogonal operator, and hence a normal operator. Moreover, we have U² = λ₁P₁ + ... + λ_kP_k = T.
(d) By the spectral theorem for normal operators, we can write T = λ₁P₁ + ... + λ_kP_k, where λ₁, ..., λ_k are the distinct eigenvalues of T and P₁, ..., P_k are orthogonal projections onto the corresponding eigenspaces. Moreover, we have T⁻¹ = λ₁⁻¹P₁ + ... + λ_k⁻¹P_k if all the eigenvalues are nonzero. Indeed, if all the eigenvalues are nonzero, then T is invertible and hence bijective. It follows that each eigenspace has a dimension at most 1, and hence T has a unique decomposition into a sum of orthogonal projections onto its eigenspaces. It is then easy to check that T⁻¹ has the desired decomposition. Conversely, suppose that T⁻¹ has the desired decomposition. Then we have T(T⁻¹(v)) = v for any v ∈ V. It follows that each eigenspace has dimension at most 1, and hence T is bijective, and hence invertible.
(e) By the spectral theorem for normal operators, we can write T = λ₁P₁ + ... + λ_kP_k, where λ₁, ..., λ_k are the distinct eigenvalues of T and P₁, ..., P_k are orthogonal projections onto the corresponding eigenspaces. It follows that T is a projection if and only if T² = T, which is equivalent to the condition that λ_i ∈ {0, 1} for all i.
(f) By the spectral theorem for normal operators, we can write T = λ_1 P_1 + ... + λ_k P_k, where λ_1, ..., lambda_k are the distinct eigenvalues of T and P_1, ..., P_k are the orthogonal projections onto the corresponding eigenspaces. Note that T is self-adjoint if and only if T = T*, or equivalently, λ_j is real for all j. On the other hand, T = -T* if and only if λ_j = -λ_j × for all j, or equivalently, lambda_j is imaginary for all j. Thus, T = -T* if and only if each λ_j is imaginary, as desired.
Learn more about the finite-dimensional complex at
https://brainly.com/question/30531953
#SPJ4
The volume of a cone is 300 cubic
centimeters. A cylinder has the same radius
and height as the cone. What is the volume
of the cylinder?
Answers
b. What's the probability a customer who ordered pancakes came to the diner late?
c. Are breakfast choice and meal time independent? Explain.

Answers
Answer:
b. To find the probability a customer who ordered pancakes came to thediner late, we need to look at the intersection of the "pancakes" row and the "late" column. This gives us a probability of 0.1, or 10%
c. To determine whether breakfast choice and meal time are independent, we need to see if the probability of one event changes based on the occurrence of the other event. In this case, it seems that breakfast choice and meal time are not independent, as the probability of being late seems to differ based on what breakfast item the customer chose. For example, the probability of being late is higher for customers who ordered pancakes compared to those who ordered cereal. Therefore, the choice of breakfast item appears to be related to the probability of being late, and so breakfast choice and meal time are not independent.
Step-by-step explanation:
24.7% of the products in the local shop are specialty soaps. 76% of those soaps are made with fresh herbs. if there are 350 bars of specialty soap in the shop, approximately how many of them are not made with fresh herbs? round your answer up to nearest whole number
Answers
we know that 76% of the specialty soaps are made with fresh herbs, and we also know that there are a total of 350 specialty soap bars, so how many are made with fresh herbs? well, just 76% of those 350
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{76\% of 350}}{\left( \cfrac{76}{100} \right)350}\implies 266\)
The Patel family made a 6-pound turkey for dinner. If each person will eat 12 of a pound, how many people will it take to finish the turkey?
Answers
Answer:
12 pound turkey
one person eats 1 lb
12 people will eat 12 lbs
Step-by-step explanation:
Every locker at a school has a volume of 10.125 cubic feet. The length and the width are both 1.5 feet as shown below. What is the value of x? (image attached)A. 3.375B. 4.5C. 6.75D. 7.125thank you ! :)

Answers
To answer this question we will use the following formula to compute the volume of a rectangular prism:
\(Volume=length\times width\operatorname{\times}height.\)Using the given diagram we get:
\(10.125ft^3=1.5ft\operatorname{\times}1.5ft\operatorname{\times}xft.\)Simplifying the above result we get:
\(10.125ft^3=2.25xft^3.\)Dividing the above result by 2.25 cubic feet we get:
\(\begin{gathered} \frac{10.125ft^3}{2.25ft^3}=\frac{2.25xft^3}{2.25ft^3}, \\ 4.5=x. \end{gathered}\)Answer: Option B.
I am giving away 20 points have fun
Answers
Answer:
Thanks :)
Step-by-step explanation:
which term of the A.P 21,42,63,84.......is 210
Answers
Answer:
T₁₀
Step-by-step explanation:
We know the first term is 21, which is a
We work out the difference by taking 21 away from 42 which equals 21.
We then use the general formula:
Tₓ = a + (x-1)(d)
We need to find the term which equals 210
210 = 21 + (x - 1)(21)
210 = 21 - 21 + 21x
210 = 21x
x = 10
Hence it is the 10 term when the thing equals 210.
100 students went on a field trip. 6 buses were filled and 10 students traveled to the destination in cars with their parents. How many students were on each bus?
Answers
Answer:
15 students on each bus!
Step-by-step explanation:
100-10(with parents)
90÷6(how many busses)
15 students on each
The students travelling on each bus are 15.
What are arithmetic operations?The arithmetic operations are the fundamentals of all mathematical operations. The example of these operators are addition, subtraction, multiplication and division.
Total number of students is given as 100.
The students to travel on car are 10.
Then, the students to travel on bus are given by following operation as,
Total students - Students to travel on car
⇒ 100 - 10 = 90
Now, the students on each bus can be obtained by using the division operation as below,
Students to travel on bus ÷ Total number of bus
⇒ 90 ÷ 6 = 15
Hence, the number of students on each bus is obtained as 15.
To know more about arithmetic operation click on,
https://brainly.com/question/25834626
#SPJ2
...............................
Answers
Answer:
1. a = 5400
2. r = 0.96
3. Percentage decrement = 65.4%
Step-by-step explanation:
Hope this helps!! Mark me brainliest!!
QUESTION 1Given a n x m matrix A and m X p matrix B, if AB = 0 then A = 0 or B = 0.TrueFalseQUESTION 2Given an xm matrix A,an n x n identity matrix I, exists such that I, A = Al, = A.TrueFalse
Answers
Given:
\(A_{n\times m},B_{m\times p}\)If AB = 0,
Then it is not necessary that A=0 or B=0
To prove this, we consider an example:
Let n=m = p =2
Then AB is given as:
Clearly AB= 0 but A,B not equals to zero.
Hence, the given statement is not true.
Hence, the answer is false.


Translate "Twelve less than two-thirds a
number is 48" into an equation.
#17
Answers
Answer:
2/3x - 12 = 48
Step-by-step explanation:
Give the equation of a circle with a diameter that has endpoints (-7, 7) and (3, 6).
Answers
Answer:
(x + 2)^2 + (y - 6.5)^2 = 25.25
Step-by-step explanation:
We can the equation of the circle in standard form, whose general equation is:
\((x-h)^2+(y-k)^2=r^2\), where
(h, k) are the coordinates of the circle's center, and r is the radiusStep 1: We know that the diameter is simply 2 * the radius. Thus, we can find the radius by first finding the length of the diameter. To do this, we'll need the distance formula, which is:
\(d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2 }\), where
(x1, y1) is one coordinate, and (x2, y2) is the other coordinate.We can allow (-7, 7) to be our (x1, y1) and (3, 6) to be our (x2, y2) point and plug these into the formula to find d, the distance between the points and the length of the diameter:
\(d=\sqrt{(3-(-7))^2+(6-7)^2} \\d=\sqrt{(3+7)^2+(-1)^2}\\ d=\sqrt{(10)^2+1}\\ d=\sqrt{100+1}\\ d=\sqrt{101}\)
Now we can multiply our diameter by 1/2 to find the length of the radius:
r = 1/2√101
Step 2: We know that the center lies at the middle of the circle and therefore represents the midpoint of the diameter. The midpoint formula is
\(m=(\frac{x_{1}+x_{2} }{2}),(\frac{y_{1}+y_{2} }{2})\), where
(x1, y1) is one coordinate, and (x2, y2) is another coordinateWe can allow (-7, 7) to be our (x1, y1) point and (3, 6) to be our (x2, y2) point:
\(m=(\frac{-7+3}{2}),(\frac{7+6}{2})\\ m=(\frac{-4}{2}),(\frac{13}{2})\\ m=(-2,6.5)\)
Thus, the coordinate for the center are (-2, 6.5).
Step 3: Now, we can create the equation of the circle and simplify:
(x - (-2)^2 + (y - 6.5)^2 = (1/2√101)^2
(x + 2)^2 + (y - 6.5)^2 = 25.25
Adding 3 to some number, then multiplying the result by 7 gives 28 .
What was the original number ?
Answers
Answer:
1
Step-by-step explanation:
1+3 = 4 4*7 = 28
it's 1 because 28/7 = 4 and you add 3 to the number so 1 + 3 = 4 * 7 = 28 is correct.
IM BAD AT MATH HELP ME

Answers
Answer:
bro i cant see the question clearly please say in comments or say again