make b the subject of the formula a = sqrt(b+6)
Answers
Answer:
a = √(b+ 6)
a² = b + 6 (Square both sides)
b = a² - 6 (subtract 6 from both sides)
Answer:
b = a^2 - 6
Step-by-step explanation:
a = sqrt(b+6)
Find the square of both sides
a^2 = (b+6). Open brackets
a^2 = b+6
Subtract 6 from both sides
a^2 - 6 = b + 6 -6
b = a^2 - 6
Related Questions
Use a trigonometric ratio to solve for a. round to two decimal places image below giving brainliest to whoever gets it correct

Answers
Sin(37) = 0.601815023152048
Sin(37) = 10/a
a = 10/Sin(37)
a = 16.61640141122483
Rounded = 16.62
Have a good day ^^
Triangle A'B'C' is formed by a reflection over x = -1 and dilation by a scale factor of 4 from the origin. Which equation shows the correct relationship between AABO
and AA"B"C"?
S
A"B" = 4BC
BC=4A"B"
AB 1
A"B"
=
00
Answers
\(\frac{AB}{A"B"} = \frac{1}{4}\) equation clearly illustrates how AABO and AA"B"C relate to one another.
What is equation ?An equation is, for instance, 3x - 5 = 16. We can solve this equation and determine that the value of the variable x is 7.
The three main types of linear equations are the slope-intercept form, standard form, and point-slope form.
Considering the data:
Dilation by a scale factor of 4 from the origin in the form of an A'B'C' reflection over x = 1
<=> The two triangles are comparable to one another since triangles can have the same shape but differ in size, so A′′B′′C′′ is 4 times larger than ABC.
=> the connection between "ABC" and "A"B"C" .
\(\frac{AB}{A"B"} = \frac{1}{4}\)
We settle on C.
\(\frac{AB}{A"B"} = \frac{1}{4}\) equation clearly illustrates how AABO and AA"B"C relate to one another.
To know more about equation visit:-
https://brainly.com/question/29657992
#SPJ1
Solve by factoring
3x^2-x-2=0
2x^2-x=3
Answers

Find the surface area of a cylinder with a height of 8 ft and a base radius of 5 ft.
Use the value 3.14 for π, and do not do any rounding.
Be sure to include the correct unit.
Answers
Answer: 408.2 ft^2
Step-by-step explanation:
A=2πrh+2πr2
A=2(3.14)(5)(8)+2(3.14)(5)^2
A=6.28*40+6.28*25
A=251.2+157
A=408.2 ft^2
A school purchased sand to fill a sandbox on its playground. The dimensions of the sandbox in meters and the total cost of the sand in dollars are known. Which units would be most appropriate to describe the cost of the sand?
Answers
The most appropriate units to describe the cost of the sandbox would indeed be dollars.
When describing the cost of an item or service, it is essential to use the unit that represents the currency being used for the transaction. In this case, the total cost of the sand for the school's sandbox is given in dollars. To maintain consistency and clarity, it is best to express the cost in the same unit it was provided.
Using dollars as the unit for the cost allows for clear communication and understanding among individuals involved in the transaction or discussion. Dollars are widely recognized as the standard unit of currency in many countries, including the United States, where the dollar sign ($) is commonly used to denote monetary values.
Using meters, the unit for measuring the dimensions of the sandbox, to describe the cost would be inappropriate and could lead to confusion or misunderstandings. Mixing units can cause ambiguity and hinder effective communication.
Therefore, it is most appropriate to describe the cost of the sand in dollars, aligning with the unit of currency provided and commonly used in financial transactions. This ensures clarity and facilitates accurate comprehension of the cost associated with the sand purchase for the school's sandbox.
for similar questions on sandbox.
https://brainly.com/question/31290675
#SPJ8
-3(2y+4) is greater that equal to 12-4y
Answers
Answer:
y is less than or equal to -12
y<=-12
Step-by-step explanation:
Answer:
y≤12
Step-by-step explanation:
-3(2y+4)≥12-4y
-6y-12≥12-4y
-6y+4y≥12+12
-2y≥24
-2y÷2≤24÷2 (You have to flip the sign if you multiply or divide by a negative number)
y≤12
What percentage of the measurements in the data set lie to the right of the median? ___ % What percentage of the measurements in the data set lie to the left of the upper quartile? ___ %
Answers
To answer this question, we need to know the median and upper quartile of the data set. Once we have these values, we can determine what percentage of the data falls to the right of the median and to the left of the upper quartile.
Let's say the median of the data set is 50 and the upper quartile is 75. To find the percentage of measurements to the right of the median, we need to look at the data values that are greater than 50 and divide that number by the total number of measurements. Let's say there are 40 data values greater than 50 and a total of 100 measurements.
Then, the percentage of measurements to the right of the median would be:
(40/100) x 100% = 40%
To find the percentage of measurements to the left of the upper quartile, we need to look at the data values that are less than or equal to 75 and divide that number by the total number of measurements. Let's say there are 60 data values less than or equal to 75 and a total of 100 measurements. Then, the percentage of measurements to the left of the upper quartile would be:
(60/100) x 100% = 60%
Your answer:
1. 40% of the measurements lie to the right of the median.
2. 60% of the measurements lie to the left of the upper quartile (Q3).
To learn more about quartile : brainly.com/question/17198478
#SPJ11
The acceleration of an object (in m/s2) is given by the function a(t) = 6 sin(t). The initial velocity of the object is v(0) = -7 m/s. Round your answers to four decimal places. a) Find an equation v(t) for the object velocity. v(t) = Preview b) Find the object's displacement (in meters) from time 0 to time 3. Preview meters c) Find the total distance traveled by the object from time 0 to time Preview meters
Answers
a. the equation for the object's velocity is v(t) = -6 cos(t) - 1. b. the total distance traveled by the object from time 0 to time t is 6 sin(t) + t meters.
a) To find the equation for the object's velocity, we need to integrate the acceleration function with respect to time.
The integral of a(t) = 6 sin(t) with respect to t gives us the velocity function v(t):
v(t) = ∫(6 sin(t)) dt
Integrating sin(t) gives us -6 cos(t), so the equation for the object's velocity is:
v(t) = -6 cos(t) + C
To find the constant C, we use the initial velocity v(0) = -7 m/s:
-7 = -6 cos(0) + C
-7 = -6 + C
C = -1
Therefore, the equation for the object's velocity is:
v(t) = -6 cos(t) - 1
b) To find the object's displacement from time 0 to time 3, we need to integrate the velocity function over the interval [0, 3]:
Displacement = ∫[0,3] (-6 cos(t) - 1) dt
Integrating -6 cos(t) gives us -6 sin(t), and integrating -1 gives us -t. Applying the limits of integration, we have:
Displacement = [-6 sin(t) - t] from 0 to 3
Plugging in the upper and lower limits:
Displacement = [-6 sin(3) - 3] - [-6 sin(0) - 0]
Displacement ≈ -6 sin(3) + 3
Therefore, the object's displacement from time 0 to time 3 is approximately -6 sin(3) + 3 meters.
c) To find the total distance traveled by the object from time 0 to time t, we need to integrate the absolute value of the velocity function over the interval [0, t]:
Total Distance = ∫[0,t] |(-6 cos(t) - 1)| dt
Since the absolute value function makes the negative part positive, we can rewrite the equation as:
Total Distance = ∫[0,t] (6 cos(t) + 1) dt
Integrating 6 cos(t) gives us 6 sin(t), and integrating 1 gives us t. Applying the limits of integration, we have:
Total Distance = [6 sin(t) + t] from 0 to t
Plugging in the upper and lower limits:
Total Distance = [6 sin(t) + t] - [6 sin(0) + 0]
Total Distance = 6 sin(t) + t
Therefore, the total distance traveled by the object from time 0 to time t is 6 sin(t) + t meters.
Learn more about distance here
https://brainly.com/question/30395212
#SPJ11
What is the sum of the angles of a 22 sided polygon
Answers
Answer:
interior = 3600° , exterior = 360°
Step-by-step explanation:
use the formula : ( n - 2 ) * 180 ..........where n is the number of sides
here the number of sides is 22
so if fall under the formula:
( 22 - 2 ) * 180
3600° is the total sum of the interior angles.
The exterior angle formula:
360° is the sum of the exterior angles.
anyone know the answer?
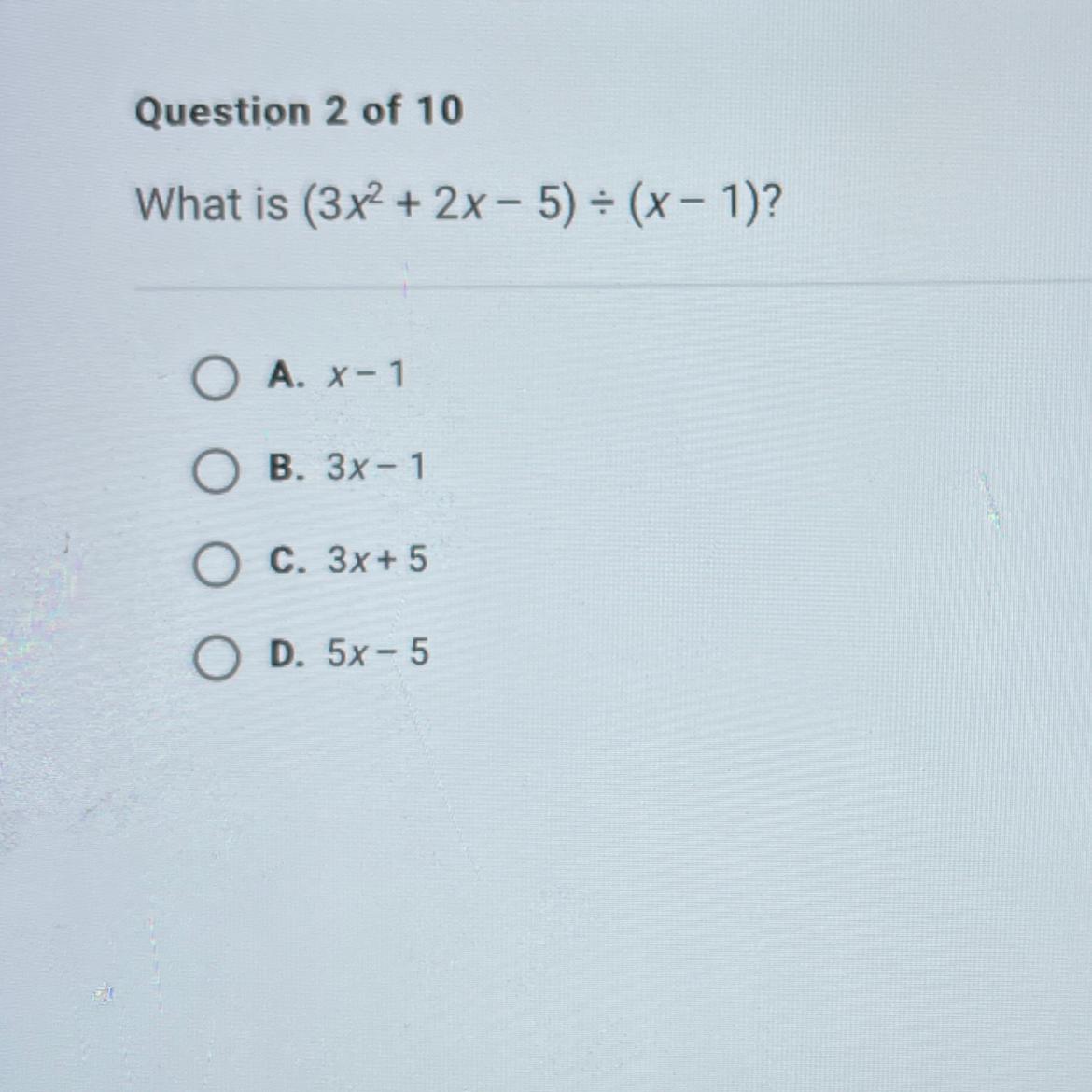
Answers
Answer:
C. 3x + 5
Step-by-step explanation:
Go to m a t h w a y . c o m (with no spaces, wont let me post without) trust me, this will save u in math
On the way back home, the Anderson family must stop at the gas station to fill up. What isthe total distance of their trip? Round your final answer to the nearest kilometer
Answers
Answer:
The total distance will remain unchanged as the gas station is on their way to home.
Step-by-step explanation:
The total distance of the trip will the distance between home to the destination and way back. If the Anderson family is stopped to fill gas in their car. The total distance of the trip is not affected by the stop in their route. If the gas station is located far from the route they follow then the distance will change.
Identify next three numbers in this sequence: 3, 12, 6, 24, 18, … 27, 13.5, 22.5 72, 66, 264 72, 36, 144 27, 21, 30
Answers
Answer:
its 72, 36, 144
Step-by-step explanation:
yes it is!!!
Convert 4500 feet per second to miles per hour 5280 ft =1 mi round to the nearest hundredth
Answers
Answer: 3067.77 miles per hour
Step-by-step explanation: To convert 4500 feet per second to miles per hour, we can use the conversion factor of 5280 feet = 1 mile.
First, let's convert 4500 feet per second to miles per second by dividing by 5280:
4500 ft/s ÷ 5280 ft/mi = 0.85227 mi/s
Next, we can convert miles per second to miles per hour by multiplying by 3600 (since there are 3600 seconds in an hour):
0.85227 mi/s × 3600 s/h = 3067.77 mi/h
Rounded to the nearest hundredth, 4500 feet per second is approximately equal to 3067.77 miles per hour.
Answer:
Hence, the correct answer = 3068.18 Miles Per Hour
Step-by-step explanation:
1 hour = 60 minutes
1 minute = 60 seconds
Then by Unitary method , 1 hour=60x60=3600 Seconds
To convert it into miles per hour I divided it by 5280 and multiply it by 3600 we get
Yesterday, between noon and midnight, the temperature dropped by 29.6°F. If the temperature was -8.6°F at midnight, what was it at noon?
Answers
Cuál lugar es más burro tu eres más burro no importa para nada se espera nada escapes burro no sirve para nada x musique
Answers
Answer:
no se perdon
Step-by-step explanation:
GG
Answer:
Step-by-step explanation:

What is the range of f(x) = -3x + 4?
Answers
Answer: In mathematics, a function is a rule that assigns each element of a set (called the domain) to a unique element in another set (called the range). The range of a function is the set of all possible output values of the function.
The range of a function can be determined by analyzing the behavior of the function as its input values change. For example, a linear function like f(x) = -3x + 4 has a slope of -3, which means that as x increases, the value of -3x decreases. This in turn means that the value of f(x) decreases as x increases.
Another important consideration in determining the range of a function is the domain of the function. The domain is the set of all possible input values of the function. If the domain is limited in some way (for example, if the function is only defined for non-negative values of x), then the range will also be limited.
In the case of f(x) = -3x + 4, the domain is all real numbers, so the range is also all real numbers. In other words, the function can take on any value on the real number line. This can be written in interval notation as (-∞, +∞) or (-∞, ∞).
I hope this explanation helps you understand the concept of the range of a function more deeply.
Step-by-step explanation:
Find the absolute maximum and minimum values of f on the set D. 31. f(x, y) = x2 + y2 – 2x, D is the closed triangular region with vertices (2, 0), (0, 2), and (0, -2) 32. f(x, y) = x + y - xy, D is the closed triangular region with vertices (0, 0), (0, 2), and (4,0) 33. f(x, y) = x2 + y2 + x²y + 4, D = {(x, y) ||x| = 1, y = 1} 34. f(x, y) = x² + xy + y2 – 6y, D = {(x, y) | -3 0, y = 0, x2 + y2 = 3} 37. f(x, y) = 2x + y4, D = {(x, y) | x2 + y2 = 1} 38. f(x, y) = x - 3x - y3 + 12y, D is the quadrilateral whose vertices are (-2, 3), (2, 3), (2, 2), and (-2,-2) 20 For functione of one riable it is cribi for a continuous
Answers
We have the following values at the vertices:
f(-2, 3) = 1, f(2, 3) = 5, f(2, 2) = 12 and f(-2, -2) = 20.
The absolute maximum value of f on D is 28, which occurs at (-2, -2). The absolute minimum value of f on D is -20, which occurs at (-2, 3).
31. To find the absolute maximum and minimum values of f on the set D, we first need to evaluate f at the vertices of the triangular region. The vertices are (2, 0), (0, 2), and (0, -2).
f(2, 0) = 4 - 4 = 0
f(0, 2) = 4 - 0 = 4
f(0, -2) = 4 - 0 = 4
So the absolute maximum value of f on D is 4, which occurs at (0, 2) and (0, -2). The absolute minimum value of f on D is 0, which occurs at (2, 0).
32. The vertices of the triangular region are (0, 0), (0, 2), and (4, 0).
f(0, 0) = 0
f(0, 2) = 2
f(4, 0) = 4
So the absolute maximum value of f on D is 4, which occurs at (4, 0). The absolute minimum value of f on D is 0, which occurs at (0, 0) and (2, 2).
33. The set D is given as {(x, y) ||x| = 1, y = 1}, which means that x can be either 1 or -1, and y is fixed at 1.
f(1, 1) = 6
f(-1, 1) = 6
So the absolute maximum value of f on D is 6, which occurs at both (1, 1) and (-1, 1). The absolute minimum value of f on D does not exist, since the set D is not a closed and bounded region.
34. The set D is given as {(x, y) | -3 < x < 0, y = 0, x^2 + y^2 = 3}, which is the part of the circle x^2 + y^2 = 3 that lies in the second quadrant.
f(-3, 0) = 12
f(0, 0) = 0
f(-sqrt(3), sqrt(6)) = 3 - 3sqrt(3)
So the absolute maximum value of f on D is 12, which occurs at (-3, 0). The absolute minimum value of f on D is 3 - 3sqrt(3), which occurs at (-sqrt(3), sqrt(6)).
37. The set D is given as {(x, y) | x^2 + y^2 = 1}, which is the unit circle centered at the origin.
f(1, 0) = 2
f(-1, 0) = -2
f(0, 1) = 1
f(0, -1) = 1
So the absolute maximum value of f on D is 2, which occurs at (1, 0). The absolute minimum value of f on D is -2, which occurs at (-1, 0).
38. The set D is the quadrilateral with vertices (-2, 3), (2, 3), (2, 2), and (-2, -2).
f(-2, 3) = -20
f(2, 3) = -4
f(2, 2) = -2
f(-2, -2) = 28
So the absolute maximum value of f on D is 28, which occurs at (-2, -2). The absolute minimum value of f on D is -20, which occurs at (-2, 3).
Learn more about Vertices:
brainly.com/question/30116773
#SPJ11
If Q is the midpoint of PR, find the coordinates of R if P(11,-2) and Q(4,3).

Answers
Answer:
R = (-3, 8).
Step-by-step explanation:
Recall the midpoint formula:
\(\displaystyle M=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
Where M is the midpoint, (x₁, y₁) is one point and (x₂, y₂) is another.
We are given that Q is the midpoint of PR, where P = (11, -2) and Q = (4, 3) and we want to find the coordinates of R.
Substitute Q for M and let P(11, -2) be (x₁, y₁). Hence:
\(\displaystyle (4, 3)=\left(\frac{11+x_2}{2}, \frac{-2+y_2}{2}\right)\)
Split into two separate equations:
\(\displaystyle \frac{11+x_2}{2}=4\text{ and } \frac{-2+y_2}{2}=3\)
Solve for each case:
\(\displaystyle 11+x_2=8\Rightarrow x_2=-3\)
\(\displaystyle -2+y_2=6\Rightarrow y_2=8\)
Therefore, our second point (x₂, y₂) is (-3, 8).
Hence, R = (-3, 8).
Answer:
(15/2),(1/2)
Step-by-step explanation:
(x1 + x2 / 2) , (y1 + y2) / 2)
(11 + 4 / 2) , (-2 + 3 / 2)
(15/2) , (1/2)
Prove the identity
1. cot²x= csc²x-1
2. sin x tan x= sec x - cos x
Answers
Answer:
Step-by-step explanation:
Hope this helps u!!

I NEED HELP ON THIS ASAP! PLEASE, IT'S DUE TONIGHT

Answers
The total length is 102.986 units
The total area of the floor sheet is 1020 units.
How to find total area?The method for finding the total area will depend on the shape(s) involved. Here are some general formulas for common shapes:
Square: To find the area of a square, multiply the length of one side by itself. For example, if the side of a square is 4 units, the area would be 4 x 4 = 16 square units.
Rectangle: To find the area of a rectangle, multiply the length by the width. For example, if a rectangle has a length of 6 units and a width of 4 units, the area would be 6 x 4 = 24 square units.
Triangle: To find the area of a triangle, multiply the base by the height and divide by 2. For example, if a triangle has a base of 5 units and a height of 8 units, the area would be (5 x 8) / 2 = 20 square units.
Circle: To find the area of a circle, multiply pi (approximately 3.14) by the radius squared. For example, if a circle has a radius of 3 units, the area would be 3.14 x 3^2 = 28.26 square units.
Read more about area here:
https://brainly.com/question/2607596
#SPJ1


Jillian is an analyst for a ride sharing app that connects users with drivers. She wonders if drivers in Dallas are more or less likely to cancel rides than drivers in Houston. She takes a random sample of 1000 rides from Dallas and finds that 30 were cancelled. A random sample of 1000 rides from Houston shows 24 cancelled rides.She used these results to test whether there is a difference in the proportion of cancelled rides between the two cities. The test statistic was z=0.83 and the p-value was approximately 0.41.At the α=0.01 level of significance, is there sufficient evidence to conclude that the proportion of cancelled rides is different between the two cities?Yes, since the p-value is greater than 0.01.Yes, since the test statistic is greater than 0.01.No, since the p-value is greater than 0.01.No, since the test statistic is greater than 0.01
Answers
No, since the p-value is greater than 0.01.
When performing a hypothesis test, we compare the p-value to the chosen level of significance, which is typically denoted by α. In this case, the level of significance is α = 0.01.
Since the p-value (approximately 0.41) is greater than the level of significance (0.01), we fail to reject the null hypothesis. The null hypothesis is that there is no difference in the proportion of cancelled rides between Dallas and Houston. Therefore, we do not have sufficient evidence to conclude that the proportion of cancelled rides is different between the two cities at the α = 0.01 level of significance.
learn about hypothesis test,
https://brainly.com/question/15980493
#SPJ11
Solve the equation f(x) = 0 to find the critical points of the given autonomous differential equation dx/dt = f(x). Then determine whether each critical point is stable or unstable. Next, solve the differential equation explicitly
dx/dt= x^2 - 5x + 4
Answers
The solution of the given differential equation is:`x(t) = 1 + (x(0)-1)/(x(0)-4).e^t.(x(0)-4)`where `x(0)` is the initial value of `x`. The given differential equation is `dx/dt = x² - 5x + 4`. To solve the differential equation, we will use the following steps:Step 1: Find the critical points of the differential equation .
Step 1: Find the critical points of the differential equation
To find the critical points of the given autonomous differential equation, we need to solve `dx/dt = 0`.So,`dx/dt = x² - 5x + 4 = 0`
Factorizing the quadratic expression, we get: `(x-1)(x-4) = 0`
Therefore, the critical points are `x = 1` and `x = 4`.Step 2: Determine whether each critical point is stable or unstableTo determine the stability of each critical point, we need to find the sign of `f'(x)` near each critical point. Here,`f'(x) = 2x - 5`At `x = 1`,`f'(x) = 2(1) - 5 = -3`
So, `f'(x) < 0` near `x = 1`.
Therefore, `x = 1` is a stable critical point.At `x = 4`,`f'(x) = 2(4) - 5 = 3`So, `f'(x) > 0` near `x = 4`. Therefore, `x = 4` is an unstable critical point.Step 3: Solve the differential equation explicitlyTo solve the given differential equation, we can use the method of separation of variables. So,`dx/dt = x² - 5x + 4`can be written as:`dx/(x² - 5x + 4) = dt`
Integrating both sides, we get: `ln|x-1| - ln|x-4| = t + C`where `C` is the constant of integration.Rewriting the above equation, we get:`ln|x-1| = ln|x-4| + t + C`
Taking the exponent of both sides, we get:`|x-1| = e^(ln|x-4| + t + C) = e^(ln|x-4|) . e^(t+C) = k.e^t.|x-4|`where `k` is the constant of integration.
Rewriting the above equation, we get:`|x-1|/|x-4| = ke^t`Since `k` is a constant, we can rewrite it as `k = |x-1|/|x-4|` for any non-zero value of `k`.
Therefore, the solution of the given differential equation is:`x(t) = 1 + (x(0)-1)/(x(0)-4).e^t.(x(0)-4)`where `x(0)` is the initial value of `x`.
To know more about differential equation visit :-
https://brainly.com/question/25731911
#SPJ11
If f(x) is a linear function, what is the value of n?
f(x)
-25
-4
-1
-10
20
o 2
o 4
5
9
9

Answers
Answer:
5
Step-by-step explanation:
EdGen 2020 answer
Answer:
c
Step-by-step explanation:
1. A team loses 20 yards and then they gain 7
yards. What integer represents the total yards
gained or lost?
Answers
Answer:
The team lost 13 yards
Step-by-step explanation:
They lose 20 then gain 7. so the equation would be 20-7=13
You have a balance of 17,426 on your credit card. Your minimum monthly payment is 461 . If your interest rate is 15.5%, how many years will it take to pay off your card assuming you don't add any debt? Enter your response to two decimal places (ex: 1.23)
Answers
With a credit card balance of $17,426, a minimum monthly payment of $461, and an interest rate of 15.5%, we need to calculate the number of years it will take to pay off the card without adding any additional debt.
To determine the time required to pay off the credit card, we consider the monthly payment and the interest rate. Each month, a portion of the payment goes towards reducing the balance, while the remaining balance accrues interest.
To calculate the time needed for repayment, we track the decreasing balance each month. First, we determine the interest accrued on the remaining balance by multiplying it by the monthly interest rate (15.5% divided by 12).
We continue making monthly payments until the remaining balance reaches zero. By dividing the initial balance by the monthly payment minus the portion allocated to interest, we obtain the number of months needed for repayment. Finally, we divide the result by 12 to convert it into years.
In this scenario, it will take approximately 3.81 years to pay off the credit card (17,426 / (461 - (17,426 * (15.5% / 12))) / 12).
Learn more about multiplying here:
https://brainly.com/question/30875464
#SPJ11
 7a) Determine the measure of the missing angle.

Answers
The measure of the missing angles are
x = 135°
y = 45°
What is a octagon?An Octagon is a polygon that has eight sides
To calculate the measure of the missing angle in the octagon, we use the formula below
Formula:
x = (n-2)180/8..............................Equation 1Where:
x = Interior angle of the octagonn = Number of sidesFrom the diagram,
n = 8 sidesSubstitute these values into equation 1
x = (8-2)180/8x = 135°Also,
x+y = 180y = 180-x.................... Equation 2Substitute the value sof x into equation 2
y = 180-135x = 45°Learn more about octagon here: https://brainly.com/question/358118
#SPJ1
Louis is saving for his retirement by making annual end of year deposits for 30 years into a bank
account that pays interest at a nominal rate of 8% compounded quarterly. For the first 10 years the
deposits are level at $5000 each year. After the 10 th year, each deposit is 3% more than the year before.
A) Give an actuarial expression for the account balance after the final deposit is made ?
B) What is the account balance after the final deposit is made ?
Answers
the actuarial expression for the account balance after the final deposit is made as:\(FV = $5000 \times [(1.03^{(n-10)}+1)(1.02)^{(204)}-1]/(0.02) + $5000 \times [(1.03^{10}+1)(1.02)^{(104)}-1]/(0.02)\)The account balance after the final deposit is made is \($62,297.36.\)
The account balance after the final deposit is made, the formula for the future value of an annuity due with a growth rate.
Actuarial expression for the account balance after the final deposit is made:
A be the annual deposit amount, n be the number of deposits, i be the nominal annual interest rate, m be the number of compounding periods per year, and g be the annual growth rate of the deposits.
The formula for the future value of an annuity due with a growth rate is:
\(FV = A \times [(1+g)\times (1+i/m)^{((n-1) \times m)+1}] / (i/m)\)
Louis' situation, we have:
\(A = $5000\) for the first 10 years, and then \(A = $5000 \times 1.03^{(n-10)}\) for the remaining 20 years.
n = 30 years
i = 8% nominal annual interest rate, compounded quarterly, so i = 2% per quarter
m = 4 quarters per year
g = 3% annual growth rate for each deposit after the 10th year
The account balance after the final deposit is made:
The above actuarial expression and substituting n=30, we get:
\(FV = $5000 \times [(1.03^{20}+1)(1.02)^{80}-1]/(0.02) + $5000 \times [(1.03^{10}+1)(1.02)^{40}-1]/(0.02)\)
Simplifying this expression gives:
\(FV = $5000 \times (1.03^{20} \times 1.02^{80} + 1.03^{10} \times 1.02^{40})\)
Using a calculator, we get:
\(FV = $5000 \times (10.4619 + 1.7958)\)
\(FV = $62,297.36\)
For similar questions on Account Balance
https://brainly.com/question/13777419
#SPJ11
Calculate the minimum number of subjects needed for a research study regarding the proportion of respondents who reported a history of diabetes using the following criteria: 95% confidence, within 5 percentage points, and a previous estimate of 0.25 288.12 0/2 pts Question 16 Calculate the minimum number of subjects needed for a research study regarding the proportion of respondents who reported a history of diabetes using the following criteria: 95% confidence, within 5 percentage points, and a previous estimate is not known 384
Answers
the minimum number of subjects needed for a research study regarding the proportion of respondents who reported a history of diabetes using the following criteria is 384.12, which can be rounded up to 385.
The minimum number of subjects needed for a research study regarding the proportion of respondents who reported a history of diabetes using the following criteria is as follows:
95% confidence, within 5 percentage points, and a previous estimate of 0.25.
The formula to calculate the sample size required for the study to determine the proportion is given by:
`n = Z²pq / E²`
Where n = sample size
Z = z-value (1.96 at 95% confidence interval)
E = margin of error
p = estimated proportion of the population
q = 1 - pp
q = estimated proportion of population without the condition (1 - 0.25 = 0.75)
Given,
Z = 1.96E = 0.05p = 0.25q = 0.75
Substituting these values in the above formula, we get;
`n = (1.96)²(0.25)(0.75) / (0.05)²``n = 384.16`
Therefore, the minimum number of subjects needed for a research study regarding the proportion of respondents who reported a history of diabetes using the following criteria is 384.12, which can be rounded up to 385.
learn more about proportion here:
https://brainly.com/question/31548894
#SPJ11
A card is drawn at random from a standard pack of playing cards.
Then a fair coin is flipped.
What is the probability of selecting a club and the coin landing on tails?
Answers
Answer:
1/8.
Step-by-step explanation:
Prob(selecting a club) = 13/52 = 1/4.
Prob(tail) = 1/2
Required probability = 1/4 * 1/2
= 1/8.
(q5) Determine whether these lines are parallel, perpendicular, or neither.

Answers
These slopes are negative reciprocals of each other (3 x -1/3 = -1). The lines are perpendicular.
When we are asked to find out if the two lines are parallel, perpendicular, or neither, we will use the slopes of the lines.
If the slopes of the lines are equal, the lines are parallel. If the slopes are negative reciprocals of each other, the lines are perpendicular.
If neither of these conditions is met, the lines are neither parallel nor perpendicular.
The slope of the line with equation y = 3x + 1 is 3. The slope of the line with equation y = -1/3x + 2 is -1/3.
To learn more about : slopes
https://brainly.com/question/16949303
#SPJ8