Miguel tracks four stocks during the day. The changes for the stocks are shown in the table. A 2-column table with 4 rows. Column 1 is labeled Stock with entries A, B, C, D. Column 2 is labeled Change with entries negative three-fourths, 0.7, negative 1, 0.2. Which list shows the values of the changes in order, from least to greatest?
Stock A, Stock B, Stock C, Stock D
Stock B, Stock D, Stock A, Stock C
Stock C, Stock A, Stock D, Stock B
Stock D, Stock C, Stock B, Stock A
Answers
The list shows the values of the changes in order, from least to greatest as Stock C, Stock A, Stock D, and Stock B which is the correct option (C).
What is descending order?Descending order is defined as when numbers (or other items) are arranged from the largest numbers to the least numbers, it is said to be in descending order.
What is ascending order?Ascending order is defined as when numbers (or other items) are arranged from the least numbers to the largest numbers, it is said to be in ascending order.
We have been given four stocks during the day. The changes for the stocks are shown in the table.
-3/4, 0.7, -1, 0.2
Here the least numbers to the largest numbers, it is said to be in ascending order.
⇒ -1 < -3/4 < 0.2 < 0.7
Arrange the stock in increasing order.
Stock C, Stock A, Stock D, Stock B
Therefore, the list shows the values of the changes in order, from least to greatest as Stock C, Stock A, Stock D, and Stock B.
Learn more about the descending order here:
brainly.com/question/233644
#SPJ1
Your question is incomplete, probably the missing part is:
Related Questions
12.- Se dispara a nivel de piso una bala de salva, su altura en metros a los t segundo está dada por la ecuación h() = −52 + 125, determina la longitud vertical máxima a la que llega.
Answers
The maximum height attained by the ball is given as follows:
75.12 m.
How to obtain the maximum height of the ball?The quadratic function that gives the height of the ball after t seconds is:
h(t) = -52t² + 125t.
The coefficients are given as follows:
a = -52, b = 125.
The t-coordinate of the vertex is given as follows:
t = -b/2a
t = 125/104
t = 1.2s.
As a < 0, we have a concave down parabola, hence the maximum height is given as follows:
h(1.2) = -52(1.2)² + 125(1.2)
h(1.2) = 75.12 m.
More can be learned about quadratic functions at https://brainly.com/question/1214333
#SPJ1
The divergence test applied to the series 3n 2n +1 tells us that the series the series converges. the series converges the series diverges. further testing is needed.
Answers
The limit of the sequence of terms of a series is zero, this test alone does not prove that the series converges, and further testing is needed to determine convergence or divergence.
The divergence test is a test used to determine if a series converges or diverges. It states that if the limit of the sequence of terms of a series is not zero, then the series diverges.
The series 3n/(2n + 1) can be simplified to
=3/2 - 3/4n + 3/4n+1.
As n approaches infinity, the terms in the series approach 3/4n, which approaches infinity as n approaches infinity.
Therefore, the limit of the sequence of terms of this series is not zero, and so the series diverges. Thus, the answer to the question is the series diverges.
A more general form of the divergence test states that if the limit of the sequence of terms of a series is not zero, then the series diverges. However, if the limit of the sequence of terms of a series is zero, this test alone does not prove that the series converges, and further testing is needed to determine convergence or divergence.
To know more about limit visit:-
https://brainly.com/question/12211820
#SPJ11
(a) Given f(x) = 2x² - x + 3. Find (z+h)-f(z), h/0 (b) Let f(x)=√(x - 2) and g(x) = x² + 7. Find the composition g[f(x)] Q-2: Solve the inequality |x - 3| ≤ 4 for the x without writing it a
Answers
a) To find (z+h)-f(z), where h ≠ 0, we substitute (z+h) and z into the function f(x) = 2x² - x + 3 and simplify the expression. The result is (z+h)-f(z) = 2(z+h)² - (z+h) + 3 - (2z² - z + 3).
b) To find the composition g[f(x)], we substitute f(x) into g(x) and simplify the expression. The result is g[f(x)] = (f(x))² + 7 = (√(x - 2))² + 7 = x - 2 + 7 = x + 5.
a) Given f(x) = 2x² - x + 3, we substitute (z+h) and z into the function to find (z+h)-f(z). We have (z+h)-f(z) = 2(z+h)² - (z+h) + 3 - (2z² - z + 3). Simplifying further, we expand the square and combine like terms, which gives us (z+h)-f(z) = 2z² + 4zh + 2h² - z - h + 3 - 2z² + z - 3. Combining like terms again, we obtain (z+h)-f(z) = 4zh + 2h² - h.
b) Let f(x) = √(x - 2) and g(x) = x² + 7. To find the composition g[f(x)], we substitute f(x) into g(x). We have g[f(x)] = g[√(x - 2)]. Simplifying further, we substitute f(x) = √(x - 2) into g(x), which gives us g[f(x)] = (√(x - 2))² + 7. Expanding the square, we have g[f(x)] = x - 2 + 7 = x + 5.
Therefore, the composition g[f(x)] is equal to x + 5.
To learn more about square click here:
brainly.com/question/30556035
#SPJ11
which type of study design is used in the following scenario: a researcher interested in the onset of early menses compared 1,000 14 year-old girls, half of whom had already begun to have monthly periods and half of whom had not. the girls were interviewed regarding previous exposures, including their prior dietary habits.
Answers
The type of study design used in the scenario you provided is a retrospective cohort study. (option b).
In this study, the researcher selected a group of 14-year-old girls and looked back in time to compare their previous dietary habits and exposures between those who had already started having monthly periods and those who had not.
It is important to note that this study design has some limitations. For instance, the researcher is relying on self-reported data from the girls, which may not always be accurate.
This study design involves selecting a group of individuals and looking back in time to compare their exposures or characteristics between those who developed the outcome of interest and those who did not. By identifying potential risk factors, the researcher can gain insights into the onset of early menses in 14-year-old girls.
Hence the correct option is (b).
To know more about study design here
https://brainly.com/question/31147631
#SPJ4
Complete Question:
Which type of study design is used in the following scenario: A researcher interested in the onset of early menses compared 1,000 14-year-old girls, half of whom had already begun to have monthly periods and half of whom had not. The girls were interviewed regarding previous exposures. including their prior dietary habits.
a) Prospective cohort study
b) Retrospective cohort study
c) Case-control study
d) Clinical trial
e) None of the answers listed
I need help finding the value of x
Answers
Answer:
x = 6
Step-by-step explanation:
From the figure attached,
∠AFB ≅ ∠EFC [Vertically opposite angles]
Since, ∠AFB and ∠EFC are the central angles subtended by arcs EC and AB.
Therefore, (21x - 9) = m(∠EFC)
(21x - 9) = m∠EFD + m∠CFD
(21x - 9) = 90° + 27°
21x = 9 + 117
21x = 126
x = 6
Therefore, x = 6 will be the answer.
A candle that is 8 inches tall burns at a rate of 3/4 inches per hour. Find the height of the candle after 4 hours.
I need an equation in slope intercept form
Answers
The equation in slope-intercept form is: y = (-3/4)x + 8
The height of the candle after 4 hours is: 5 inches.
How to Write an Equation in Slope-Intercept Form?Let's use the equation of a line in slope-intercept form, which is:
y = mx + b
Where y is the dependent variable (in this case, the height of the candle), x is the independent variable (in this case, the time), m is the slope (in this case, the rate of burning), and b is the y-intercept (in this case, the initial height of the candle).
We know that the candle is initially 8 inches tall, so b = 8. We also know that the rate of burning is 3/4 inches per hour, so m = -3/4 (negative because the candle is getting shorter).
Substituting these values into the equation, we get:
y = (-3/4)x + 8
To find the height of the candle after 4 hours, we simply plug in x = 4 and solve for y:
y = (-3/4)(4) + 8
y = -3 + 8
y = 5
Therefore, the height of the candle after 4 hours is 5 inches.
Learn more about the slope-intercept form on:
https://brainly.com/question/1884491
#SPJ1
Please help I will mark brainliest answer !
Answers
Answer:
the answer is D.
Step-by-step explanation:
math and my 6th grade year
A line contains the points (-26, -37) and (-32, -61)
What is the slop of the line in simplified form?
Answers
Answer:
The slope is 4
Step-by-step explanation:
We can find the slope by using
m = ( y2-y1)/(x2-x1)
= ( -61- -37)/( -32 - -26)
= ( -61+37)/( -32 +26)
= -24/-6
=4
Answer:
\( slope = 4 \)
Step-by-step explanation:
(-26, -37) and (-32, -61)
\( slope = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( slope = \dfrac{-61 - (-37)}{-32 - (-26)} \)
\( slope = \dfrac{-24}{-6} \)
\( slope = 4 \)
give an example of a random variable x whose expected value is 5, but the probability that x = 5 is 0
Answers
An example of a random variable x whose expected value is 5 but has zero probability of taking the value 5 is a discrete random variable that follows a skewed distribution.
One such example is a random variable representing the number of goals scored by a soccer team in a game, where the average number of goals is 5 but it is extremely unlikely for the team to score exactly 5 goals in a single game.
Let's consider a scenario where a soccer team's average number of goals scored in a game is 5. However, due to various factors such as the team's playing style, opponent's defense, or other external factors, it is highly improbable for the team to score exactly 5 goals in any given game. This situation can be represented by a discrete random variable x, where x represents the number of goals scored by the team in a game.
The probability distribution of x would show a low probability mass at x = 5, indicating that the probability of the team scoring exactly 5 goals is close to zero. However, the expected value of x, denoted as E(x), would still be equal to 5 due to the influence of other possible goal-scoring outcomes and their corresponding probabilities.
In summary, this example demonstrates that even though the expected value of a random variable is 5, it does not necessarily imply that the variable will actually take on the value 5 with a non-zero probability.
Learn more about probability here: brainly.com/question/31828911
#SPJ11
Express 7.051 in the form of p/q
Answers
7.051 can be written as the fraction 7051/1000.
To express 7.051 as a fraction in the form of p/q, we need to identify the decimal places and convert them to the corresponding fractional parts.
Since 7.051 has three decimal places, we multiply it by 1000 to move the decimal point three places to the right, which gives us 7051.
Now, the numerator (p) of the fraction will be 7051, and the denominator (q) will be the corresponding power of 10, which is 1000.
Therefore, 7.051 can be expressed as 7051/1000.
To simplify this fraction, we can divide both the numerator and the denominator by their greatest common divisor (GCD).
In this case, the GCD of 7051 and 1000 is 1, so the fraction is already in its simplest form.
For similar question on fraction.
https://brainly.com/question/20712359
#SPJ8
1+1=?
5
2
4
7
this question is really hard and confusing
Answers
Answer:
I think it is 2
Step-by-step explanation:
I hope this is right! Please Rate Brainiest!
Answer:
its obv 478
Step-by-step explanation:
1+1=2 divoided by 400=294-478
The mean time required to repair breakdowns of a certain copying machine is 93 minutes. The company which manufactures the machines claims that breakdowns of its newer model are easier to fix. To test this claim, a sample of 18 breakdowns of the new model were observed, resulting in a mean repair time of 86.8 minutes with a standard deviation of 14.6 minutes. Using a significance level of a = 0.10, determine if the new copy machines are faster to repair. State clearly what your null and alternative hypotheses are, show your work, and state your conclusion.
Answers
A significance level of 0.10, we have enough evidence to conclude that the new copy machines have a significantly faster mean repair time compared to the older model.
To test if the new copy machines are faster to repair, we can set up the following null and alternative hypotheses:
Null Hypothesis (H₀): The mean repair time for the new copy machines is the same as the mean repair time for the older model.
Alternative Hypothesis (H₁): The mean repair time for the new copy machines is less than the mean repair time for the older model.
Let's perform a one-sample t-test to test these hypotheses. The test statistic is calculated as:
t = (sample mean - population mean) / (sample standard deviation / √(sample size))
Given:
Population mean (μ) = 93 minutes
Sample mean (\(\bar x\)) = 86.8 minutes
Sample standard deviation (s) = 14.6 minutes
Sample size (n) = 18
Significance level (α) = 0.10
Calculating the test statistic:
t = (86.8 - 93) / (14.6 / sqrt(18))
t = -6.2 / (14.6 / 4.24264)
t ≈ -2.677
The degrees of freedom for this test is n - 1 = 18 - 1 = 17.
Now, we need to determine the critical value for the t-distribution with 17 degrees of freedom and a one-tailed test at a significance level of 0.10. Consulting a t-table or using statistical software, the critical value is approximately -1.333.
Since the test statistic (t = -2.677) is less than the critical value (-1.333), we reject the null hypothesis.
To know more about significance level:
https://brainly.com/question/4599596
#SPJ4
Example 2: Solve the system algebraically. Then check your answer graphically.
y = x² + 8x + 13
y = 2x+5
1-25
YEXZ18413
Answers
Answer: (-2, 1), (-4, -3)
Step-by-step explanation:
y = x² + 8x + 13
y = 2x+5
x² + 8x + 13 = 2x+5
x² + 6x + 13 = 5
x² + 6x + 8 = 0
x² + 2x + 4x + 8 = 0
(x+2)(x+4)=0
x=-2 or x=-4
y=2(-2)+5
y=-4+5
y=1
y=2(-4)+5
y=-8+5
y=-3
o of the four expressions x y, x 5y, x – y, and 5x – y are chosen at random, what is the probability that their product will be of the form of x 2 – (by) 2 , where b is an integer?
Answers
The probability of the product of the given expressions is in the form of x² - (by)² is equal to 1/6.
As given in the question,
Given four expressions are:
( x + y ) , ( x + 5y ) , ( x - y ) and ( 5x - y )
Product of any two expression to have two degree expressions :
( x + y )( x + 5y ) = x² + 6xy + 5y²
( x + y )( x - y ) = x ² - y²
( x + y )( 5x - y ) = 5x² + 4xy -y²
( x + 5y )( x - y ) = x² + 4xy -5y²
( x + 5y )( 5x - y ) = 5x² + 24xy -5y²
(x - y) ( 5x - y) = 5x² - 6xy + y²
Total number of possible outcome of the product with degree 2 = 6
Favourable outcomes in the form of x² - ( by )² is x² - y² = x² -(1y)²
Here b = 1 is an integer.
Number of favourable outcomes = 1
Required probability = 1/6
Therefore, the probability of the product in the form of x² - ( by )² is equal to 1/6.
The complete question is:
If two of the four expressions x + y, x + 5y, x – y, and 5x – y are chosen at random, what is the probability that their product will be of the form of x2 – (by)2, where b is an integer?
Learn more about probability here
brainly.com/question/11234923
#SPJ4
Select the correct answer. what is the value of the third quartile of the data set represented by this box plot? a box plot with lower quartile, median and upper quartile values as 21, 26, and 29, respectively. the whiskers on both the ends end at 19 (minimum) and 33 (maximum). a. 19 b. 21 c. 26 d. 29
Answers
Answer:
D. 29
Step-by-step explanation:
just did the test and got it correct. Edmentum, Plato.
Rewrite each expression using distributive property.
6(y + 7) please help!!!!!
Answers
Answer:
6y + 42
Step-by-step explanation:
Answer: 6y+42
Step-by-step explanation:
When you distribute, you multiply the coefficient by each term in the parenthesis.
6y+42
g the top and bottom margins of a poster are each 12 cm and the side margins are each 8 cm. if the area of printed material on the poster is fixed at 1536 cm2, find the dimensions of the poster with the smallest cmheight cm
Answers
Using differentiation and area of a rectangle, the dimensions of the poster with the smallest height are 24 cm x 216 cm.
What is the dimensions of the poster with the smallest height?
Let x = width of printed material
Total width = printed material width + left margin + right margin
Total width = x + 8 + 8 = x + 16 cm
Total height = printed material height + top margin + bottom margin
Total height = 1536/x + 12 + 12 = 1536/x + 24 cm
The total area of the poster is the product of the width and height:
Total area = Total width * Total height
1536 = (x + 16) * (1536/x + 24)
To find the dimensions of the poster with the smallest height, we can find the minimum value of the total height. To do this, we can differentiate the equation with respect to x and set it to zero:
d(Total height)/dx = 0
Differentiating the equation and simplifying, we get:
1536/x² - 24 = 0
Rearranging the equation, we have:
1536/x² = 24
Solving for x, we find:
x² = 1536/24
x² = 64
x = 8 cm
Substituting this value back into the equations for total width and total height, we can find the dimensions of the poster:
Total width = x + 16 = 8 + 16 = 24 cm
Total height = 1536/x + 24 = 1536/8 + 24 = 192 + 24 = 216 cm
Learn more on area of rectangle here;
https://brainly.com/question/25292087
#SPJ4
60 Points for answering
Thanks and a 5 star rating
Must Answer in: 10 min and Brainly for the right answer
The expression 2(l + w) is used to calculate the perimeter of a rectangle, where l is length and w is width. If the length is \(\frac{2}{5}\) unit and the width is \(\frac{1}{5}\), what is the perimeter of the rectangle in units?
\(\frac{3}{5} \ \textless \ br /\ \textgreater \ \ \textless \ br /\ \textgreater \
1 Unit\ \textless \ br /\ \textgreater \ \ \textless \ br /\ \textgreater \
1\frac{1}{5} \ \textless \ br /\ \textgreater \ \ \textless \ br /\ \textgreater \
2\frac{3}{5}\)
Answers
The expression for calculating the perimeter of a rectangle is given by 2(l + w), where l is the length and w is the width of the rectangle. Given that the length of the rectangle is \(\frac{2}{5}\) units and the width is \(\frac{1}{5}\) units, we can substitute these values in the expression for perimeter.
Perimeter = 2(l + w)
Substituting the values of length and width, we get:
Perimeter = 2(\(\frac{2}{5}\) + \(\frac{1}{5}\))
Perimeter = 2([tax]\frac{3}{5}\))
Perimeter = \(\frac{6}{5}\)
Therefore, the perimeter of the rectangle is \(\frac{6}{5}\) units.
Hence, the correct answer is \(\frac{6}{5}\).
To find the perimeter of a rectangle with length l and width w, we can use the expression 2(l + w). Given that the length is \(\frac{2}{5}\) units and the width is \(\frac{1}{5}\) units, we can substitute these values into the expression:
Perimeter = 2(\(\frac{2}{5}\) + \(\frac{1}{5}\))
First, we add the fractions:
\(\frac{2}{5}\) + \(\frac{1}{5}\) = \(\frac{3}{5}\)
Now, we multiply the result by 2:
2 * \(\frac{3}{5}\) = \(\frac{6}{5}\)
The perimeter of the rectangle is \(\frac{6}{5}\) units, which is equivalent to 1\(\frac{1}{5}\) units.
To know more about perimeter visit:-
https://brainly.com/question/6465134
#SPJ11
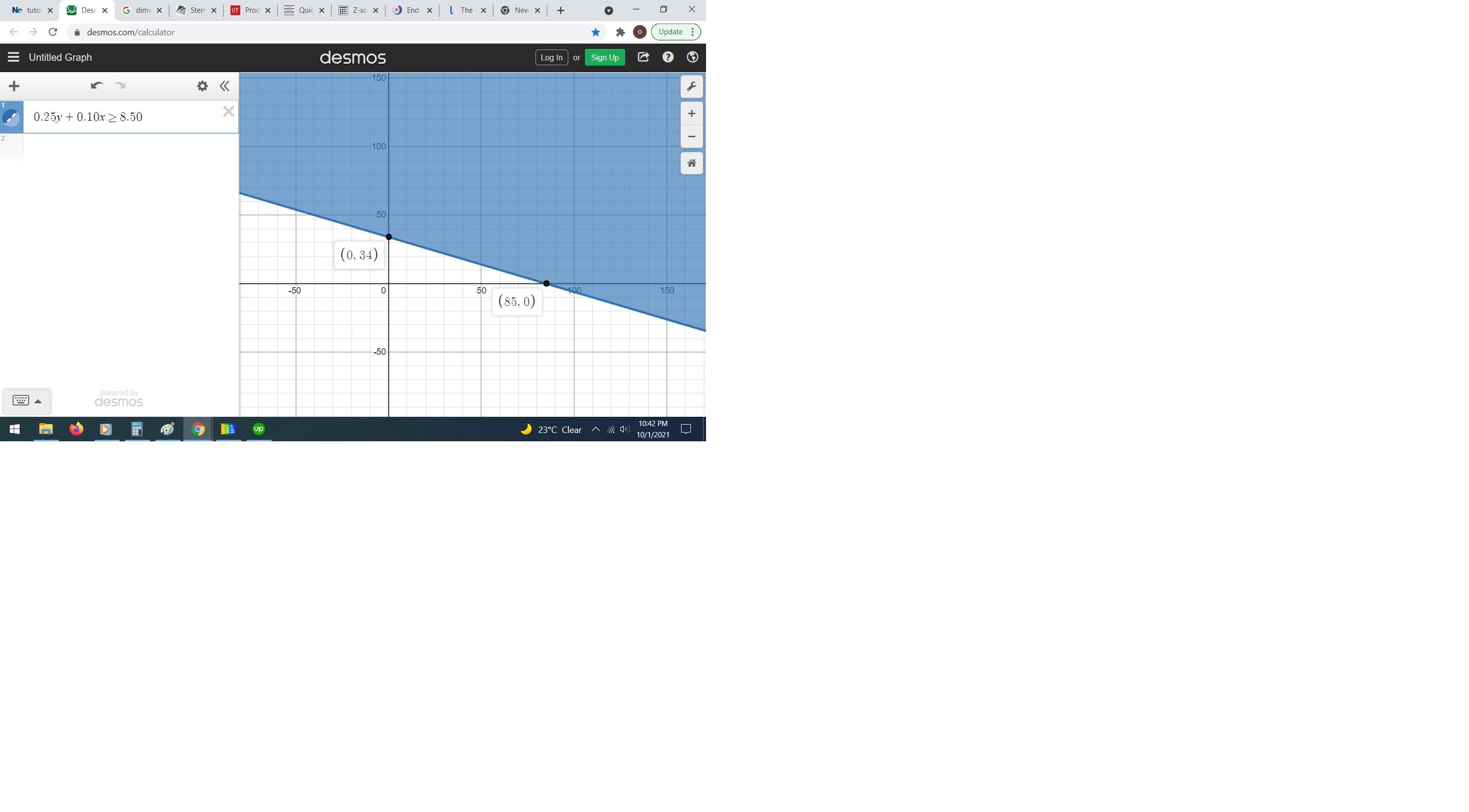
4. Tyler filled a small jar with quarters and dimes and donated it to his school'scharity club. The club member receiving the jar asked, "Do you happen toknow how much is in the jar?" Tyler said, "I know it's at least $8.50, but I don'tknow the exact amount."4a. Write an inequality to represent the relationship between the numberof dimes, d, the number of quarters, q, and the dollar amount of the moneyin the jar.
Answers
Let
y -----> number of quarters
x ----> number of dimes
we have that
the inequality that represents this situation is
Remember that
1 quarter =$0.25
1 dime=$0.10
so
\(0.25y+0.10x\ge8.50\)rewrite the variables
\(0.25q+0.10d\ge8.50\)see the attached figure to better understand the problem
Part 4b
The solution of the given inequality is the shaded area above the solid line 0.25q+0.10d=8.50
A solution to this inequality could be the point (50,50)
that means
the number of quarters is 50 and the number of dimes is 50
the ordered pair must satisfy the inequality
Verify
\(\begin{gathered} 0.25q+0.10d\ge8.50 \\ 0.25(50)+0.10(50)\ge8.50 \\ 12.50+5\text{ }\ge8.50 \\ 17.50\text{ }\ge8.50\text{ --}\longrightarrow\text{ is ok} \end{gathered}\)Part 4c
we have that
d=25 dimes
substitute in the inequality and solve for q
so
\(0.25q+0.10(25)\ge8.50\)solve for q
\(\begin{gathered} 0.25q+2.5\ge8.50 \\ 0.25q\ge8.50-2.5 \\ 0.25q\ge6 \\ q\ge24 \end{gathered}\)the number of quarters must be greater than or equal to 24
Determine if the sequence below is arithmetic or geometric and determine the
common difference / ratio in simplest form.
19, 10, 1, ...
Answers
Answer:
arithmetic sequence
Step-by-step explanation:
There is a common difference d between consecutive terms, that is
d = 10 - 19 = 1 - 10 = - 9
This means the sequence is arithmetic
Simplify the following expression
by combining like terms.
3z + 2 - 2 + 8 = [? ]z +
Answers
Answer:
3z+8
Step-by-step explanation:
3x+2−2+8
=3x+2+−2+8
Combine Like Terms:
=3x+2+−2+8
=(3x)+(2+−2+8)
=3x+8
PLS HELP ME!!
The inverse of a function occurs when _____.
the domain remains the same, but the range is written as a reciprocal
the range and the domain are interchanged
both the domain and the range are reciprocals
the range remains the same, but the domain is written as a reciprocal
Answers
Answer:
the domain and range are interchanged
Step-by-step explanation:
given a function f(x) with known domain and range
then for the inverse function \(f^{-1}\) (x)
its domain is the range of f(x) and
its range is the domain of f(x)
that is the domain and the range are interchanged.
Natalie's family drank 0.9 of the 2.6 liters of the lemonade she made for a picnic. how much lemonade did her family drink? Show your work.
Answers
Answer:
There is 1.7 left
Step-by-step explanation:
2.6 - 0.9 = 1.7
Please help thank you. The question is in the picture.
Answers
the dilation factor is 1/2 because the new shape is half the size
Find the linear function with the following properties.
f(-4) = 7
f(-8) = -4
Answers
Answer:
\(\mathsf{ y=\dfrac{11}{4}x+18}\)
Step-by-step explanation:
\(\mathsf{(x_1,y_1)=(-4,7)}\)
\(\mathsf{(x_2,y_2)=(-8,-4)}\)
\(\mathsf{slope \ (m)=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{-4-7}{-8+4}=\dfrac{11}{4}}\)
\(\mathsf{y-y_1=m(x-x_1)}\)
\(\mathsf{\implies y-7=\dfrac{11}{4}(x+4)}\)
\(\mathsf{\implies y=\dfrac{11}{4}x+18}\)
URGENT 50 PTS
In ALMO, Point C is the intersection of the blue and green segments. If CM = 11, QM = 5, PL = 6, RM = 10, CO =9.8, and LC = 2x + 5, solve for X
Answers
explanation:
1. 42.78 + 19.56
2. 0.0997 + 1.4
3. $62.74 + $1.75 + $12
4. 40.75 – 17. 46
5. 0.95 – 0.68
6. $60 - $31.74
7. 5.4 x 0.07
8. 5.9 x 1.2
9. 0.24 ÷ 0.8
10. 6.56 ÷ 4
Answers
1. - 62.34
2. - 1.4997
3. - $76.49
4. - 23.29
5. - 0.27
6. - $28.26
7. - 0.378
8. - 7.08
9. - 0.3
10. - 1.64
Answer:
1. 62.34
2. 1.4997
3. $76.49
4. 23.29
5. 0.27
6. $28.26
7. 0.378
8. 7.08
9. 0.3
10. 1.64
1 4/9 divided by -2/9
Answers
Answer:
6 1/2
Step-by-step explanation:
change 1 4/9 into a improper fraction, which is 13/9, and when dividing fractions flip the second number upside down then multiply. 13/9 times -2/9 is -117/18. simplify, which is 13/2, which is also equal to 6 1/2. hope this helped
50 PTS & BRAINLIEST! PLEASE HELP ASAP! Add one number to each column of the table so that it shows a function. Do not repeat an ordered pair that is in the table
Answers
The additional ordered pair to form the function (12, 7)
What is function?A function is a relation for which each value from the set the first components of the ordered pairs is associated with exactly one value.
Given that, a table which is showing a function,
We need to find one ordered pair that can shows a function,
According to the definition of the function, we know that each value of x will have a unique value of y,
From the numbers given, the only ordered pair that shows a function is (12, 7)
Hence, the additional ordered pair to form the function (12, 7)
Learn more about functions, click;
https://brainly.com/question/12431044
#SPJ1
Please help me ASAP!!!
Answers
Answer:
the third one (2,-18)
Step-by-step explanation: