mrs. gordon bought a stove which cost $850. no down payment was required. mrs. gordon has to pay $160 for the next six months. what is the average amount she pays in interest each month?
Answers
Answer:
the average amount Mrs. Gordon pays in interest each month, we need to determine the total interest paid over the six-month period and divide it by the number of months.
The total interest paid can be found by subtracting the cost of the stove from the total amount paid over six months:
Total interest paid = Total amount paid - Cost of the stove
The total amount paid over six months is calculated by adding the monthly payments:
Total amount paid = $160/month * 6 months
Let's perform the calculations:
Total amount paid = $160/month * 6 months = $960
Total interest paid = Total amount paid - Cost of the stove
= $960 - $850
= $110
Now, to find the average amount Mrs. Gordon pays in interest each month, we divide the total interest paid by the number of months:
The average amount paid in interest each month = Total interest paid / Number of months
= $110 / 6 months
≈ $18.33
Therefore, Mrs. Gordon pays an average of approximately $18.33 in interest each month.
Related Questions
There is a proportional relationship between the number of quarts and number of gallons for liquid measurements. What constant of proportionality relates gallons to quarts?
Answers
The value of constant of proportionality that relates gallons to quarts is 0.25 .
A constant of proportionality may be a constant worth for the magnitude relation of 2 proportional quantities. If the magnitude relation or product is constant, the 2 variables area unit proportional. the worth of the constant of quotient depends on the kind of relationship between the 2 given quantities (positive versus inverse variation).As we all know that one gallon have four quartz.
The proportional relation is written as y = kx.
We know that y varies proportionately with x.
Substitute within the such that x = four and y = one values and solve for k.
1 = k(4)
k =1 /4 = 0.25
Therefore the constant of proportionality is 0.25
Learn additional regarding about constant of proportionality here :
https://brainly.com/question/1835116
#SPJ9
Write each expression in expanded form. Then rewrite the product in exponential form.Only do A, B, and C
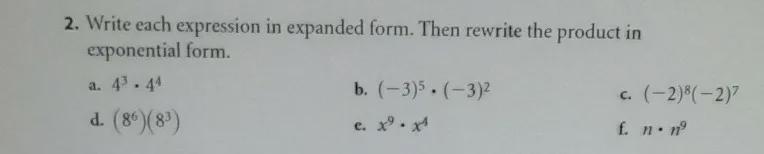
Answers
Write each expression in expanded form.
(a)
\(\begin{gathered} 4^{3\text{ }}.4^4=4^3\times4^4 \\ =4\times4\times4\times4\times4\times4\times4 \end{gathered}\)(b)
\(\begin{gathered} (-3)^5.(-3)^{2\text{ }}=(-3)^5\text{ }\times(-3)^2 \\ =(-3)^{}\times(-3)^{}\times(-3)^{}\times(-3)^{}\times(-3)\times(-3)\times(-3) \end{gathered}\)(c)
\(\begin{gathered} (-2)^8.(-2)^7=(-2)^8\text{ }\times(-2)^7 \\ =(-2)^{}\times(-2)\text{ }\times(-2)^{}\times(-2)\times(-2)\times(-2)\times(-2)\times(-2)\times(-2)\times(-2)\times(-2)\times(-2)\times(-2)\times(-2)\times(-2) \end{gathered}\)Rewriting in exponential form
(a)
\(\begin{gathered} 4^3.4^4=4^{3+4} \\ \text{ = 4}^7 \end{gathered}\)(b)
\(\begin{gathered} (-3)^5.(-3)^2=(-3)^{5+2} \\ \text{ = (-3)}^7 \end{gathered}\)(c)
\(\begin{gathered} (-2)^8.(-2)^7=(-2)^{8+7}\text{ } \\ =(-2)^{15} \end{gathered}\)2. The table includes results from polygraph experiments. In each case, it was known if the
subject lied or did not lie, so the table indicates when the polygraph test was correct. Find the
test statistic needed to test the claim that whether a subject lies or does not lie is independent of
the polygraph test indication.
Polygraph test indicated
that the subject lied.
Polygraph test indicated
that the subject did not lie.
025.571
Did the Subject Actually Lie?
No (did not lie) Yes (lied)
15
32
42
9
(1 poir

Answers
We cannot conclude that whether a subject lies or does not lie is independent of the polygraph test indication.
How to explain the hypothesisThe test statistic needed to test the claim that whether a subject lies or does not lie is independent of the polygraph test indication is the chi-square statistic.
In this case, the grand total is 90. The row totals are 57 and 33, and the column totals are 42 and 48. The expected frequencies are as follows:
The chi-square statistic is calculated as 0.177. The p-value for the chi-square statistic is calculated using a chi-square table. The degrees of freedom for the chi-square table are the number of rows minus 1, multiplied by the number of columns minus 1.
Since the p-value is greater than 0.05, we fail to reject the null hypothesis. We cannot conclude that whether a subject lies or does not lie is independent of the polygraph test indication.
Learn more about hypothesis on
https://brainly.com/question/11555274
#SPJ1
Here are the heights (in inches) of 8 students in a seminar.
63, 69, 60, 66, 70, 59, 64, 67
What is the percentage of these students who are shorter than 65 inches'
Answers
Answer:
50%
Step-by-step explanation:
there are 8 students and 4 are shorter than 65 inches.
So 4 divided by 8 = 0.5 or 50%
These ^ r all below 65
4 numbers are under 65, and four aren’t, therefore there are eight numbers in total
4/8= 1/2= .5 = 50%
50% of these students are under 65 inches
Hope I helped! Please mark brainliest
Calculate the expectation value of and for a particle in the state n = 5 moving in a one dimensional box of length 2.50 × 10−10. Is =2. Explain
Answers
The expectation values are <x> = 1.25 x 10⁻¹⁰ , <x²> = 2.07 x 10⁻²⁰
What is average?
The middle number, which is determined by dividing the sum of all the numbers by the total number of numbers, is the average value in mathematics. When determining the average for a set of data, we add up all the values and divide this sum by the total number of values.
We need to find expectation value of <x> and < x²>
average value for <x> is given by a/2 where a = length of box
hence <x> = ( (2.5 x 10⁻¹⁰) /2) = 1.25 x 10⁻¹⁰
hence <x²> = (1.25 x 10⁻¹⁰)² = 1.56 x 10⁻²⁰
<x²> = ( a/2 x 3.14 x n)² x ( 4 x 3.14² x n² /3 -2)
hence <x²> = ( 2.5 x 10⁻¹⁰ / 2 x 3.14 x 5)² x ( 4 x 3.14² x 5² /3 -2)
<x²> = 2.07 x 10⁻²⁰
<x²> is not equal to <x>²
The expectation values are <x> = 1.25 x 10⁻¹⁰, <x²> = 2.07 x 10⁻²⁰
To learn more about the average from the given link
https://brainly.com/question/1136789
#SPJ4
Given the graph of f (x), determine the domain of f –1(x).
Radical function f of x that increases from the point negative 3 comma negative 2 and passes through the points 1 comma 0 and 6 comma 1

Answers
The domain of the function f(x) that has a range of [-2, ∞) is [-2, ∞)
What is the inverse of a function?The inverse of a function that maps x into y, maps y into x.
The given coordinates of the points on the radical function, f(x) are; (-3, -2), (1, 0), (6, 1)
To determine the domain of
\( {f}^{ - 1}( x)\)
The graph of the inverse of a function is given by the reflection of the graph of the function across the line y = x
The reflection of the point (x, y) across the line y = x, gives the point (y, x)
The points on the graph of the inverse of the function, f(x), \( {f}^{ - 1} (x)\) are therefore;
\(( - 3, \: - 2) \: \underrightarrow{R_{(y=x)}} \: ( - 2, \: - 3)\)
\(( 1, \: 0) \: \underrightarrow{R_{(y=x)}} \: ( 0, \: 1)\)
( 6, \: 1) \: \underrightarrow{R_{(y=x)}} \: ( 1, \: 6)
The coordinates of the points on the graph of the inverse of the function, f(x) are; (-2, -3), (1, 0), (1, 6)
Given that the coordinate of point (x, y) on the image of the inverse function is (y, x), and that the graph of the function, f(x) starts at the point (-3, -2) and is increasing to infinity, (∞, ∞), such that the range of y–values is [-2, ∞) the inverse function, \( {f}^{ - 1}( x)\), which starts at the point (-2, -3) continues to infinity, has a domain that is the same as the range of f(x), which gives;
The domain of the inverse of the function, \( {f}^{ - 1}( x)\), using interval notation is; [-2, ∞)
Learn more about the inverse of a function here:
https://brainly.com/question/3831584
#SPJ1
Write 10 3 without an exponent what number Is this ? 5.102+ 3
Answers
The value of 10^3 in standard form is 1000
Exponents and valuesGive the exponential form 10^3
This means the product of 10 in 3 places. Mathematically;
10^3 = 10 * 10 10 * 10
10^3 = 100 * 10
10^3 = 1000
Hence the value of 10^3 in standard form is 1000
Learn more on standard form here: https://brainly.com/question/19169731
Use the limit definition of the derivative to find the slope of the tangent line to the curve

Answers
EXPLANATION
The given function is defined by
\(\begin{gathered} f(x)=6x-5 \\ at\text{ x= -4} \end{gathered}\)the slope of a tangent line, the instantaneous rate of change of a function
\(f^{\prime}(x)_{\lim _{\square}x\Rightarrow a}=\frac{f(x)-f(a)}{x-a}\)Thus, we will have
\(\begin{gathered} a=-4 \\ f^{\prime}(x)=\frac{6x-5-(6\times-4-5)}{x-(-4)}=\frac{6x-5+29}{x+4}=\frac{6x-24}{x+4} \\ as\text{ } \\ \lim _{x=a} \\ \text{Applying L'hopital rule} \\ f^{\prime}(x)=\frac{6}{1}=6 \end{gathered}\)Therefore, the slope will be 6
Which property justifies the statement below? X(y+5)=xy+5x
Answers
Using your own words, create a word problem around the given problem. Then solve it
65% of $300
Answers
Answer:
Philip got $300 from his relatives, he puts 65% of the money he got into the bank. How much money did Philip put in the bank? $195
2. Solve the application problem.
Find the area of a mirror that measures 2 yards by 7/8 yard.
A. 1 3/4 yd^2
B. 5 3/4 yd
C. 1 3/4 yd
D. 5 3/4 yd^2
Answers
Answer:
Area = l × w
= 2 × 0.875
= 1 3/4 yd^2 or 1.75 yd^2
hope i helped
Step-by-step explanation:
Which equation represents a tangent function with a domain of all Real numbers such that x is not equal to pi over 2 plus pi times n comma where n is an integer?

Answers
Based on the information given, the equation that represents the tangent function will be D. j(x) = tan(x/2 - π).
Solving the domain.Based on the information given, we are informed that we should get the equation that represents a tangent function with a domain of all real numbers such that x is not equal to pi over 2 plus pi times n comma where n is an integer.
Based on the information given, the undefined function will be when the input values equal x = π/2 + nπ. Therefore, from the options given, the equation that represents this will be j(x) = tan(x/2 - π).
Learn more about domain on:
https://brainly.com/question/1428378
Answer: g(x)=tan(x-π)
Step-by-step explanation:
graph all of themwatch how all of them touch π over 2 except g(x)
Can someone please tell me if this is a function and also provide a easy explanation on how it is the answer? (30 pts)

Answers
The relationship in the figure is a function because each input has only one output to which they are linked
What is a function?A function is a definition or rule that maps each element in a set of input values to exactly one element in a set output values.
The data in the sets can be presented as follows;
x \({}\) f(x)
-1 \({}\) → 2
0\({}\) → 2
1\({}\) → -3
2\({}\) → -2
8\({}\) → 3
The above table indicates that each x-value has only one f(x) value, which indicates that the relationship s a function. The relationship is still a function with the presence of an f(x) value, 2, having two x values, -1 and 0, as the condition satisfies the definition of a function.
Learn more on functions here: https://brainly.com/question/29869165
#SPJ1
in the expression 7a + b-12 which is a constant
Answers
Answer: Its -12
Step-by-step explanation:
In Algebra, a constant is a number on its own.
Equation Inequality
A.4
B.3
C.7
D.6
E.5

Answers
Answer:
Option A
Step-by-step explanation:
If we try the options, y will be 4
option A
Can someone please help me
I’m not good at math and I need to multiply this
135
x 62
Answers
what is greatest common factor of -x^2+6x-19
Answers
The greatest common factor of -x^2 + 6x - 19 is 1.
To find the greatest common factor (GCF) of the polynomial \(-x^2 + 6x - 19,\) we need to factorize the polynomial and identify the common factors among its terms.
First, let's examine the polynomial and see if we can factor it further:
\(-x^2 + 6x - 19\)
The polynomial does not appear to have any common factors among its terms.
It cannot be factored using simple integer factors.
In this case, we can say that the GCF of the given polynomial is 1.
It is important to note that the GCF represents the highest degree of common factors that can be factored out from all terms of a polynomial. In this particular case, the polynomial does not possess any common factors that can be factored out.
It's worth mentioning that this polynomial is already in its simplest form and cannot be factored further.
However, if the polynomial had common factors that could be factored out, such as common binomial factors or other mathematical patterns, the GCF would differ from 1.
But in this case, the polynomial does not exhibit any common factors beyond 1.
For similar question on greatest common factor.
https://brainly.com/question/25266622
#SPJ8
Given that TU=8x+11 and UV=12x−1, what are x, TU, UV, and TV?
Answers
Answer:
x = 3TU = UV = 35TV = 70Step-by-step explanation:
The question lacks the required diagram. Find the diagram attached.
From the diagram, it can be seen that point U is the midpoint of T and V. This means that TU = UV
Given TU=8x+11 and UV=12x−1
8x+11 = 12x -1
8x-12x = -1-11
-4x = -12
x = 3
Since TU = 8x+11
TU = 8(3)+11
TU = 24+11
TU = 35
Also UV = 12x-1
UV = 12(3)-1
UV = 36- 1
UV = 35
TV = TU+UV
TV = 35+35
TV = 70

Which is the correct equation for a line that passes through the points (-2,7) and (2,-5)?
y=3x+5
y=1/3x+3
y= -3x-12
y= -3x+1
Answers
Answer:
y= -3x+1
Step-by-step explanation:
x1= -2 x2=2 y1=7 y2=-5
using the formula
(y-y1)/(x-x1)=(y2-y1)/(x2-x1)
(y-7)/(x-(-2))=(-5-7)/(2-(-2))
(y-7)/(x+2)=(-5-7)/(2+2)
(y-7)/(x+2)=(-12)/4
(y-7)/(x+2)=-3
cross multiply
y-7=-3(x+2)
y-7=-3x-6
y=-3x-6+7
y=-3x+1
Eureka math lesson 7 problem set 6.5
Answers
In a bag of marbles, there are 8 blue marbles and 5 green marbles.
If there are 25 green marbles, how many blue marbles will be there ?
Answers
Ratio of blue marbles to green marbles
= 8:5
= 8×5:5×5
= 40:25
So, if there are 25 green marbles then there are 40 blue marbles.
An experiment was conducted by having a group of children solve a puzzle. It was found that of those who had solved the puzzle on a given trial, 40% could solve it on the next trial. And of those who couldn't solve the puzzle on a given trial, 10% could solve it on the next trail. At the present time, 80% of the children solved the puzzle on the current trial, but 20% did not. Assume that this process can be modeled as a Markov process.
Write the transition matrix. Label the columns and rows, using S for "able to solve" and NS for "not able to solve.
Write the initial distribution matrix.
What percent of the children will be able to solve the puzzle on the next trial (trial 1)?
What percent of the children will be able to solve the puzzle on trial 2?
After many trials, what percent of the children will fail to solve the puzzle on each trial?
Answers
Answer:
I hope this helps!
Step-by-step explanation:
Please mark brainiest

what is 20 times 20plz tell me
Answers
Answer:
400
Step-by-step explanation:
Given: ,
bisects ∠AEC.
A horizontal line has points A, E, D. 2 lines extend from point E. One line extends to point B and another extends to point C. A small box represents the angle for C E D.
What statements are true regarding the given statement and diagram?
∠CED is a right angle.
∠CEA is a right angle.
m∠CEA = One-half(m∠CEB)
m∠CEB = m∠BEA
m∠DEB = 135°
m∠AEB = 35°
Answers
Answer:
angle ced is a right ange
so the m angels debate =135 m angle aeb =35
so the answer is 135+35 =170
180 is a all side sim
=180-170=10 answer
Answer:
∠CED is a right angle.
∠CEA is a right angle.
m∠CEB = m∠BEA
m∠DEB = 135°
y=300(1+0.06/12)^12t
i need to answer. no links or I'll report
Answers
-
If you were to solve for t it’d be “t=In(y/300)/12In(1.005)
Consider a circle with centre O and chords AB and CD.chord AB = Chord CD . Prove that arc AB = arc CD
Answers
The proof that arc AB = arc CD is shown below
How to prove that arc AB = arc CD Given a circle with center O and chords AB and CD,
Such that AB = CD.
Considering a point P on arc AB and a point Q on arc CD
Such that AP = BP and CQ = DQ
Since OP = OQ and P and Q are on arcs AB and CD respectively,
It follows that angle POQ is equal to half the central angle of the circle that subtends the same arc as chord AB.
Similarly, arc AB is equal to the central angle of the circle that subtends arc CD.
Therefore:
POQ i= 1/2 * central angle of the circle and
Arc CD subtends twice the central angle as POQ.
Since the central angles subtended by arc AB and arc CD are equal, it follows that the arcs themselves are equal, i.e., AB = CD.
Read more about circle at
https://brainly.com/question/25871159
#SPJ1
On an exam with μ = 52, you have a score of X = 56. Which of the following values for the standard deviation would give you the highest position in the class distribution? a. σ = 2 b. σ = 8 c. σ = 10 d. σ = 4
Answers
Answer:
σ = 2 (option a)
Step-by-step explanation:
You would want the smallest standard deviation possible.
Think of it like this: if everyone, other than you, got only 50, 51, 52, 53 then you would be the ultimate highest position in the class.
As opposed to being an average position if the scores were about 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 ---your score would not put you in the highest position in the class distribution.
So, a standard deviation of σ = 2 would give you the highest position in the class distribution.
use the virtical line test to determine which group does not represent a function
Answers
Answer:
I just explained the verticle line test
Step-by-step explanation:
the verticle line test is if you draw a line at x=(insert x-value in question) and it hits more than two points from that equation then that does not pass the verticle line test. In the picture I attached, the green funtion(circle) does not pass the verticle line test because it hits x=1(black line) in more than one place while the red function(exponential function) passes the verticle line test because it hits x=1 at only one point.

Use an appropriate series to find Taylor series of the given function centered at the indicated value of a. Write your answer in summation notation.
sinx, a= 2π
Answers
Answer:
The Taylor series is \($$\sum_{n=0}^{\infty} [\frac{(-1)^n}{(2n +1)!} (x)^{2n+1}]\)
Step-by-step explanation:
From the question we are told that
The function is \(f(x) = sin (x)\)
This is centered at
\(a = 2 \pi\)
Now the next step is to represent the function sin (x) in it Maclaurin series form which is
\(sin (x) = \frac{x^3}{3! } + \frac{x^5}{5!} - \frac{x^7}{7 !} +***\)
=> \(sin (x) = $$\sum_{n=0}^{\infty} [\frac{(-1)^n}{(2n +1)!} (x)^{2n+1}]\)
Now since the function is centered at \(a = 2 \pi\)
We have that
\(sin (x - 2 \pi ) = (x-2 \pi ) - \frac{(x - 2 \pi)^3 }{3 \ !} + \frac{(x - 2 \pi)^5 }{5 \ !} - \frac{(x - 2 \pi)^7 }{7 \ !} + ***\)
This above equation is generated because the function is not centered at the origin but at \(a = 2 \pi\)
\(sin (x-2 \pi ) = $$\sum_{n=0}^{\infty} [\frac{(-1)^n}{(2n +1)!} (x - 2 \pi)^{2n+1}]\)
Now due to the fact that \(sin (x- 2 \pi) = sin (x)\)
This because \(2 \pi\) is a constant
Then it implies that the Taylor series of the function centered at \(a = 2 \pi\) is
\($$\sum_{n=0}^{\infty} [\frac{(-1)^n}{(2n +1)!} (x)^{2n+1}]\)
A rhombus and a triangle are equal in areas. if the base and height of the triangle are 24.8 cm and 5.5 cm respectively and the length of one diagonal of the rhombus is 22 cm, find the length of other diagonal of the rhombus.
Answers
As we know that
Area of triangle = ½ × Base × Height
Area = ½ × 24.8 × 5.5Area = 1 × 12.4 × 5.5Area = 12.4 × 5.5Area = 68.2 cm²Now,Area of rhombus = ½ × D1 × D2
68.2 = ½ × 22 × D268.2 × 2 = 22 × D2136.4 = 22 × D2136.4/22 = D26.2 = D2D2=6.2Hence :-Other Diagonal is 6.2 cm.\(\begin{gathered} \\ \end{gathered}\)