On a normal curve the center of the range of scores is represented by the what
Answers
On a normal curve, the center of the range of scores is represented by the mean
In a normal distribution, the center of the range of scores is represented by the mean or average of the scores. The normal distribution is a symmetrical bell-shaped curve, with the mean in the center, and the standard deviation determining the width of the curve. The mean is also the point of highest frequency, where the curve is highest.
The normal distribution is widely used in statistics and is a fundamental concept in many fields. It is used to describe real-world phenomena, such as heights or weights of people, test scores, and many other variables. Understanding the normal distribution is crucial in statistical analysis and decision making.
Learn more about mean here
brainly.com/question/31101410
#SPJ4
Related Questions
Sara drives 96 miles on 3.2 gallons of gas. She uses this information to calculate how many m
Using this result, how many miles can Sara drive on 12.5 gallons of gas?
O 37.5
O2.4
O 375
O 240
Answers
Given: Kite ABDC with diagonals AD and BC intersecting at E.
Prove: AD bisects BC
с
E
B
Determine the missing reasons in the proof.
Statement
ABDC is a kite.
CD
AD
ACDA
ABDA
ZCDA ZBDA
ED ED
ACED ABED
CE BE
D
Reason
given
BD and AC AB definition of a kite
AD
reflexive property of congruence
CPCTC
reflexive property of congruence
CPCTC

Answers
Reflexive property of congruence CPCTC .
What is the congruence property?When two objects or figures have the same size and shape, the term "congruence" is used to describe it. Congruence has the transitive property, which states that if two sets of lines, angles, or triangles are congruent with a third pair of lines, angles, or triangles, then the first pair of lines, angles, or triangles are also congruent with the third pair of lines, angles, or triangles. As was previously mentioned, the transitive property creates an equivalence relationship between 3 lines, 3 angles, and 3 triangles. According to the definition of the transitive property of congruence in geometry, if any two angles, lines, or forms are, respectively, congruent with a third angle, line, or shape, then the first two angles, lines, or shapes are likewise congruent with the third angle, line, or shape.
To know more about congruency ,visit:
brainly.com/question/2039214
#SPJ13
Answer:
The answer to the first box is SSS criterion, im not sure about the second box, i know it isnt ASA criterion, but i hope this helps!
Step-by-step explanation:
Drag the tiles to the boxes to form correct pairs. Not all tiles will be used. Match the resulting values to the corresponding limits.

Answers
The correct solution to the limits of x in the tiles can be seen below.
\(\mathbf{ \lim_{x \to 9^+} (\dfrac{|x-9|}{-x^2-34+387}) }\)\(\mathbf{ = -\dfrac{1}{52} }\)\(\mathbf{ \lim_{x \to 8^-} (\dfrac{8-x}{|-x^2-63x+568|}) }\)\(\mathbf{=\dfrac{1}{79} }\)\(\mathbf{ \lim_{x \to 7^+} (\dfrac{|-x^2-17x+168| }{x-7}) }\)= -31 \(\mathbf{ \lim_{x \to 6^-} (\dfrac{|x-6| }{-x^2-86x+552}) }\)\(\mathbf{ =\dfrac{1}{98}}\)What are the corresponding limits of x?The limits of x approaching a given number of a quadratic equation can be determined by knowing the value of x at that given number and substituting the value of x into the quadratic equation.
From the given diagram, we have:
1.
\(\mathbf{ \lim_{x \to 9^+} (\dfrac{|x-9|}{-x^2-34+387}) }\)
So, x - 9 is positive when x → 9⁺. Therefore, |x -9) = x - 9
\(\mathbf{ \lim_{x \to 9^+} (\dfrac{x-9}{-x^2-34+387}) }\)
Simplifying the quadratic equation, we have:
\(\mathbf{ \lim_{x \to 9^+} (-\dfrac{1}{x+43}) }\)
Replacing the value of x = 9
\(\mathbf{ = (-\dfrac{1}{9+43}) }\)
\(\mathbf{ = -\dfrac{1}{52} }\)
2.
\(\mathbf{ \lim_{x \to 8^-} (\dfrac{8-x}{|-x^2-63x+568|}) }\)
-x²-63x+568 is positive when x → 8⁻.Thus |-x²-63x+568| = -x²-63x+568
\(\mathbf{ \lim_{x \to 8^-} (\dfrac{1}{x+71}) }\)
\(\mathbf{=\dfrac{1}{8+71} }\)
\(\mathbf{=\dfrac{1}{79} }\)
3.
\(\mathbf{ \lim_{x \to 7^+} (\dfrac{|-x^2-17x+168| }{x-7}) }\)
x -7 is positive, therefore |x-7| = x - 7\(\mathbf{ \lim_{x \to 7^+} (\dfrac{-x^2-17x+168 }{x-7}) }\)
\(\mathbf{ \lim_{x \to 7^+} (-x-24)}\)
\(\mathbf{ \lim_{x \to 7^+} (-7-24)}\)
= -31
4.
\(\mathbf{ \lim_{x \to 6^-} (\dfrac{|x-6| }{-x^2-86x+552}) }\)
x-6 is negative when x → 6⁻. Therefore, |x-6| = -x + 6\(\mathbf{ \lim_{x \to 6^-} (\dfrac{-x+6 }{-x^2-86x+552}) }\)
\(\mathbf{ \lim_{x \to 6^-} (\dfrac{1}{x+92}) }\)
\(\mathbf{ \lim_{x \to 6^-} (\dfrac{1}{6+92}) }\)
\(\mathbf{ =\dfrac{1}{98}}\)
Learn more about calculating the limits of x here:
https://brainly.com/question/1444047
#SPJ1
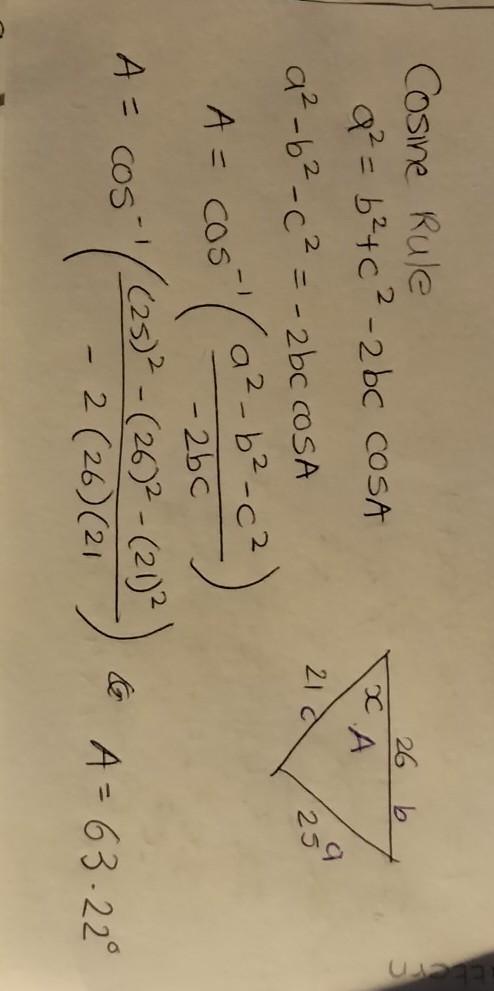
if 26, 25, 21 are the sides of a triangle what is x =?
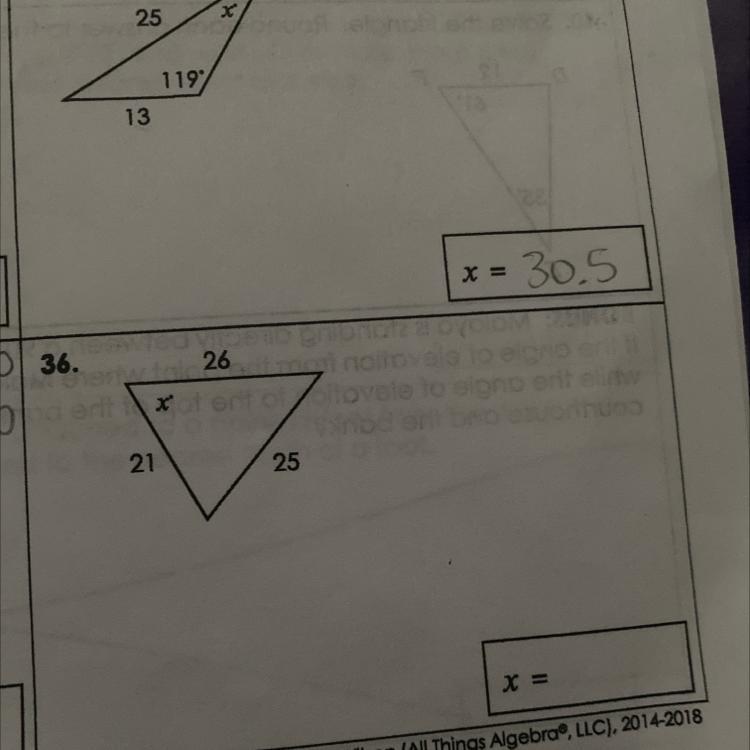
Answers
Answer:
63.22⁰
Step-by-step explanation:
the answer is in the picture. please mark mine brainliest.
2×5²-5!
Pls help dong...
Answers
Answer:
45
Step-by-step explanation:
I think it's 45. Why do I have to have 25 characters
Answer:
5^2 is 5x5=25 25x 2 = 50 minus 5 is 45 so i think its 45
Step-by-step explanation:
Help, please!!! Quick! If 2 answers I will vote one brainliest!

Answers
Answer:
37
Step-by-step explanation:
180 - 45 - 98 = 37
Answer:
37. ...... yeah.......
Date:
1) Write the equation of the piecewise function shown in the graph,
(Only the first one)

Answers
Answer:
4'F
Step-by-step explanation:
If m∠A = m∠B and m∠A + m∠C = ∠D, then
m∠B + m∠C = ∠D.
Which property is shown?
reflexive property
substitution property
symmetric property
transitive property
Answers
Answer:
Substitution Property
Step-by-step explanation:
The change from the first equation to the final equation is m∠A has been replaced by m∠B. In other words, m∠B was substituted for m∠A.
Answer:
Substitution property
Step-by-step explanation:
Have a nice day!
a parallelogram has sides of lengths 9 and 8, and one angle is 45°. find the lengths of the diagonals. (round your answers to two decimal places. enter your answers as a comma-separated list.)
Answers
Answer:
6.57 units; 15.71 units-------------------------
Let the diagonals be d₁ and d₂.
One of the diagonals has opposite angle 45° and the other one- 135° since adjacent angles of a parallelogram add to 180°.
Use the law of cosines to find diagonals.
Find d₁:
\(d_1=\sqrt{8^2+9^2-2*8*9*cos(45 deg)} =\sqrt{43.18} =6.57\ rounded\)Find d₂:
\(d_2=\sqrt{8^2+9^2-2*8*9*cos(135 deg)} =\sqrt{246.82} =15.71\ rounded\)The lengths of the diagonals of the parallelogram are approximately 12.73 and 15.56 units, respectively.
To determine the lengths of the diagonals of a parallelogram, we can use the law of cosines. Let's denote the lengths of the diagonals as d1 and d2. Given that the sides of the parallelogram are 9 and 8, and one angle is 45°, we can use the following calculations:
For diagonal d1:
d1^2 = 9^2 + 8^2 - 2 * 9 * 8 * cos(45°)
d1 ≈ 12.73
For diagonal d2:
d2^2 = 9^2 + 8^2 - 2 * 9 * 8 * cos(135°)
d2 ≈ 15.56
Therefore, the lengths of the diagonals are approximately 12.73 and 15.56, respectively.
To know more about parallelogram refer here:
https://brainly.com/question/16985034#
#SPJ11
PLEASE HELP I WILL REWARD BRAINLY. PLEASE ONLY ANSWER IF YOU KNOW HOW TO SOLVE THIS PROBLEM. PLEASE INCLUDE INSIGHTFUL EXPLAINATION AND THOUGHT PROCESS: A woman and her two children are playing on a seesaw. This seesaw has seats that can move to different distances from the fulcrum. Riders can also add seats to the seesaw. The woman weighs 145lb, her son weighs 95lb, her daughter weighs 70lb, each seat weighs 5 pounds. Question: The woman is on the left side of the seesaw, 60 inches from the fulcrum. The daughter and son both get on the right side. The son sits 60 inches from the fulcrum. Where should the daughter sit to balance the seesaw. Please explain your process and give correct answer.
Answers
Answer: 40 inches
Step-by-step explanation:
The woman weight and the seat will be: 145lb + 5lb = 150lb,
her son weight and the seat will be: 95lb + 5lb = 100lb
her daughter weight and the seat will be: 70lb + 5lb = 75lb
Given that the woman is on the left side of the seesaw, 60 inches from the fulcrum. The moment of the woman will be 150 × 60 = 9000
The daughter and son both get on the right side.
If the son sits 60 inches from the fulcrum, his moment will be:
100 × 60 = 6000
The sum of the moment of the son and daughter must be equal to the moment of their mother.
Let the position of the daughter = X
The moment of the daughter will be:
75 × X = 75X
Equate the moment of the mother to the sum of the moment of her children
9000 = 6000 + 75X
Collect the like terms
75X = 9000 - 6000
75X = 3000
X = 3000/75
X = 40
The position the daughter should sit to balance the seesaw is 40 inches away from seasaw to the right.
A company has $36,000 to hire a mathematician and his or her secretary. Out of respect for the mathematician's training, the mathematician will be paid $8000 more than the secretary. How much will each be paid
Answers
The money paid to the secretary is $14000 and the money paid to mathematician is $22000.
What is an equation?A mathematical statement that establishes the equality of two mathematical expressions is the called an equation.
Total money available for hiring = $36000
Let the money given to secretary = X
Money given to the mathematician = X + 8000
X + (X + 8000) = 36000
2X = 28000
X = 14000
Money given to secretary is $14000.
Money given to the mathematician is $22000.
Learn more about equations on:
https://brainly.com/question/2972832
#SPJ4
HELP I WILL GIVE BRAINLIEST!!

Answers
Answer:
x=40
Step-by-step explanation:
2x+7+x-10+63=180
3x=120
x=40
Find X Y and Z for brainliest

Answers
Answer:
12 z
22.5x or 3 meybe
where Y?????
Step-by-step explanation:
Answer:
Step-by-step explanation:
I'm going to assume that y is the length of the red line.

If z=x.f(XY), express x (dz/DX) - y (dz/Dy) in its simplest
form
Answers
The expression x(dz/dX) - y(dz/dy) can be written as:
x(dz/dX) - y(dz/dy) = x * (x * d/dX[f(XY)]) - y * (x * d/dy[f(XY)])
To express the expression x(dz/dX) - y(dz/dy) in its simplest form, let's differentiate z = x * f(XY) with respect to X and y.
Using the product rule, we differentiate z with respect to X:
dz/dX = x * d/dX[f(XY)] + f(XY) * d/dX[x]
Since f(XY) does not depend on X, the second term on the right-hand side simplifies to zero:
dz/dX = x * d/dX[f(XY)]
Next, we differentiate z with respect to y:
dz/dy = x * d/dy[f(XY)]
Now, we can substitute these derivatives into the expression x(dz/dX) - y(dz/dy):
x(dz/dX) - y(dz/dy) = x * (x * d/dX[f(XY)]) - y * (x * d/dy[f(XY)])
Simplifying further:
x(dz/dX) - y(dz/dy) = x^2 * d/dX[f(XY)] - yx * d/dy[f(XY)]
This is the simplest form of the expression, given the information provided.
However, without knowing the specific form or properties of the function f(XY), we cannot simplify it any further.
Note that the result may vary depending on the specific function f(XY) and the nature of its dependencies on X and y.
Therefore, the expression x(dz/dX) - y(dz/dy) can be written as:
x(dz/dX) - y(dz/dy) = x * (x * d/dX[f(XY)]) - y * (x * d/dy[f(XY)])
To know more about expression refer here:
https://brainly.com/question/28170201#
#SPJ11
write the mixed number 11 1/6 as a decimal
Answers
Answer:
11.1667
Step-by-step explanation:
11 1/6
11*6+1
=67/6
=11.1666666666
=11.1667
whats commutative property of multiplication.
Answers
Answer:
The commutative property is a math rule that says that the order in which we multiply numbers does not change the product.
Step-by-step explanation:
Find the geometric mean between 4 and 6. (Always simplify the radical completely.)

Answers
Answer:
Use the formula to find the geometric mean.
√
4
⋅
6
Multiply
4
by
6
.
√
24
Rewrite
24
as
2
2
⋅
6
.
Tap for more steps...
√
2
2
⋅
6
Pull terms out from under the radical.
2
√
6
Approximate the result.
4.89897948
The geometric mean should be rounded to one more decimal place than the original data. If the original data were mixed, round to one decimal place more than the least precise.
4.9
what is the difference between mutiplying and adding polynomials
Answers
Answer:
When you add polynomials, you combine only like terms together. When you multiply polynomials, you multiply all pairs of terms together.
Step-by-step explanation:
.
Answer:
adding, subtracting and multiplying polynomials are, basically, the same as adding, subtracting and multiplying numbers. They only difference is that we have a pesky variable to worry about
Identify the surface with the given vector equation. r(s, t) = (s cos(t), s sin(t), s) circular paraboloid O elliptic cone O hyperbolic paraboloid O plane O circular cone X
Answers
The surface with the given vector equation, r(s, t) = (s cos(t), s sin(t), s), is a circular cone.
The vector equation r(s, t) = (s cos(t), s sin(t), s) represents a surface in three-dimensional space. Let's analyze the equation to determine the nature of the surface.
In the equation, we have three components: s, cos(t), and sin(t). The presence of s indicates that the surface expands or contracts radially from a central point. The trigonometric functions cos(t) and sin(t) determine the angle at which the surface extends in the x and y directions.
By observing the equation closely, we can see that as s increases, the radius of the surface expands uniformly in all directions, while the height remains constant. This behavior is characteristic of a circular cone. The circular base of the cone is defined by s cos(t) and s sin(t), and the vertical component is determined by s.
Therefore, the surface described by the vector equation r(s, t) = (s cos(t), s sin(t), s) is a circular cone.
Learn more about vector equation here :
https://brainly.com/question/32619742
#SPJ11
60 degrees 30 degrees 72 degrees 46 83 97 215 457

Answers
suppose the matrix, , has eigenvectors , , and whose eigenvalues are , and respectively. then, using the same order, can be written in the form where
Answers
We can write A = PAP where 1 P= and A= where P is an invertible matrix that maps the null space of A to itself.
To find the matrix P, we need to solve the following system of linear equations:
λ_1 1 = 1
λ_2 (-4) 1 = 1
λ_3 (-1) 1 = 1
The eigenvalues are real and non-negative, so they can be written as λ = λ_1, λ_2, λ_3 = λ_1, -4, -1 respectively.
Using Cramer's rule, we have:
\(λ_1 * 1^T = 1 * 1^T = 1\)
\(λ_2 * (-4)^T = -4 * 1^T = -4\)
\(λ_3 * (-1)^T = (-1) * 1^T = -1\)
Multiplying the first and third equations, we get:
\(-λ_1 * λ_3 = -4 * (-1) = 4\)
Multiplying the second and third equations, we get:
\(-λ_2 * λ_3 = -4 * (-1) = 4\)
Subtracting the second equation from the first, we get:
\(λ_1^2 - λ_2^2 = 1^2 - (-4)^2 = 5\)
Multiplying the first and third equations, we get:
\(-λ_1 * λ_2 = -4 * (-1) = 4\)
Dividing the third equation by the second equation, we get:
\(-1/λ_2 = -1/λ_3\)
Taking the reciprocal of both sides, we get:λ_2 = λ_3
Substituting this into the second equation, we get:
-\(λ_1 * λ_3 = -4 * (-1) * λ_3 = -4\)
Simplifying, we get:
-4 = -4
This equation has no solution, so the matrix A cannot be written in the form A = PAP where 1 P= and A= Thus, the answer is no.
To know more about invertible matrix
https://brainly.com/question/31062095
#SPJ4
Full Question: the matrix, A, has eigenvectors and whose eigenvalues are 1, –4 and – 1 respectively. Then, using the same order, A can be written in the form A = PAP where 1 P= and A=
Find two ratios that are equivalent to 15/36.
A.) 5/12 and 45/72
B.) 5/12 and 30/72
C.) 15/12 and 30/72
D.) 12/5 and 72/30
Answers
The two ratios that are equivalent to 15/36 are expressed as: B.) 5/12 and 30/72.
What are Equivalent Ratios?If two ratios are said to be equivalent, it means that they will have the same value when simplified or expressed in their simplest form.
Given the ratio, 15/36, simplify in its simplest form:
15/36 = 5 * 3 / 12 * 3 = 5/12
So also, we have:
30/72 = 5 * 6 / 6 * 12 = 5/12
Therefore, 5/12 and 30/72 are equivalent to the ratio, 15/36.
Learn more about equivalent ratios on:
https://brainly.com/question/13513438
#SPJ1
pls answer. On a coordinate plane, a line with a 90-degree angle crosses the x-axis at (negative 4, 0), turns at (negative 1, 3), crosses the y-axis at (0, 2) and the x-axis at (2, 0). What is the range of the function on the graph? all real numbers all real numbers less than or equal to –1 all real numbers less than or equal to 3 all real numbers less than or equal to 0

Answers
Range: All real numbers greater than or equal to 3. The Option C.
What is the range of the function on the graph formed by the line?To find the range of the function, we need to determine the set of all possible y-values that the function takes.
Since the line crosses the y-axis at (0, 2), we know that the function's range includes the value 2. Also, since the line turns at (-1, 3), the function takes values greater than or equal to 3.
Therefore, the range of the function is all real numbers greater than or equal to 3.
Read more about Range
brainly.com/question/14209611
#SPJ1
Question 2 of 10
Which of the following statements must be true about this diagram? Check
all that apply.
A. y+z=w
B. X+ y = w
C. Z>X
D. x + y = 2
DE. W X
F.W>Y
I
PREVIOUS
Answers
Answer:
A E F
Explanation:
Rules to know:
Triangles = 180 degrees
Straight lines = 180 degrees (example z + w = 180)
Therefore: angles of straight line = angles of triangle
A : w is an obtuse angle (greater than 90) and x is acute (less than 90)
E : w is obtuse whereas y is acute.
F : Since triangle = 180 = x + y + z
Straight line = 180 = z + w
Equate the two:
z + w = x + y + z (subtract z from both sides)
w = x + y
Equate the two z + w = x + y + z (subtract z from both sides) w = x + y
Solve the following equation for f. Be sure to take into account whether a letter is capitalized or not.
N2=6f+H

Answers
Answer:
f = (N² - H)/6
Step-by-step explanation:
Step 1: Write equation
N² = 6f + H
Step 2: Solve for f
Subtract H on both sides: N² - H = 6fDivide both sides by 6: (N² - H)/6 = fRewrite: f = (N² - H)/6Which series of transformations shows that pentagon A is congruent to pentagon B?
A.
Reflect pentagon A over the y-axis, rotate it 180° clockwise about the origin, and translate it 3 units up.
B.
Rotate pentagon A 90° counterclockwise about the origin, reflect it over the x-axis, and translate it 8 units to the right and 1 unit up.
C.
Rotate pentagon A 90° clockwise about the point (3, 1), reflect it over the x-axis, and translate it 3 units to the left.

Answers
The series of transformations shows that pentagon A is congruent to pentagon B is
A. Reflect pentagon A over the y-axis, rotate it 180° clockwise about the origin, and translate it 3 units up.
How to find the transformationTo determine which series of transformations shows that pentagon A is congruent to pentagon B, we need to study the transformations that maps A to B
Reflect pentagon A over the y-axis, brings the image to the 2nd quadrant
Also, rotate it 180° clockwise about the origin, this movement brings the pentagon to the 4th quadrant
Then translate it 3 units up maps it to pentagon B
Learn more about transformations at
https://brainly.com/question/4289712
#SPJ1
I can't figure this out

Answers
Answer:
D
Step-by-step explanation:
I believe its D due to the fact when lined up from the point both wrenches align
WILL MARK BRAINLIET IF GOTTEN RIGHTTT DONT ANSWER IF U DONT KNOWWW

Answers
Answer:
H
Step-by-step explanation:
sorry if im wrong
Answer:
H
Step-by-step explanation:
A translation from the point (3,2) 1 unit to the left and two units down leaves you at (2,0). A reflection across the y-axis leaves you at point (-2, 0). A 90 degree counterclockwise rotation about the origin leaves you at point (0,-2), which is also point H.
Tia's tent is in the form of a triangular prism as shown below.
If Tia plans to waterproof the tent, excluding the base, what
is the area in which she will waterproof?
(round to the nearest hundredth)

Answers
Answer: 279.43
Step-by-step explanation:

The area of the tent that she will need to waterproof is 279.43 feet².
What is Surface Area?The area of a three dimensional object on it's outer surface is called the surface area of the object.
Given a tent in the form of a triangular prism as given.
We have to find the surface area of the tent excluding the base.
There are 2 triangular faces and 2 rectangular faces.
Area of the prism that needs to waterproof = area of 2 rectangles + area of 2 triangles
Area of rectangles = 2 × 14 × 8 = 2 × 112 feet² = 224 feet²
Height of the triangular face = √(8² - 4²) = √48
Area of 2 triangles = 2 × 1/2 × 8 × (√48) = 8√48 feet²
Area needed to be waterproofed = 224 feet² + 8√48 feet² = 279.43 feet²
Hence the area of the tent is 279.43 feet².
Learn more about Surface area here :
https://brainly.com/question/29101132
#SPJ2
2. The elevator in the Washington Monument takes 75 seconds to travel 506 feet to the top floor. What is the speed of the elevator in miles per hour
Answers
Answer: the speed of the elevator is 4.6 miles per hour.
Step-by-step explanation:
Given, The elevator in the Washington Monument takes 75 seconds to travel 506 feet to the top floor.
Since 1 hour = 3600 seconds
⇒ 1 second = \(\dfrac{1}{3600}\) hour
⇒ 75 seconds = \(\dfrac{75}{3600}\) hour \(=\dfrac{1}{48}\) hour
1 mile = 5280 feet
1 feet = \(\dfrac{1}{5280}\) mile
506 feet = \(\dfrac{506}{5280}\) miles \(=\dfrac{23}{240}\) miles
Speed = \(\dfrac{Distance}{Time}\)
\(=\dfrac{\dfrac{23}{240}}{\dfrac{1}{48}}\\\\=\dfrac{23\times48}{240}\\\\=\dfrac{23}{5}\\\\=4.6\text{ miles per hour}\)
Hence, the speed of the elevator is 4.6 miles per hour.