Paula works part time ABC Nursery. She makes $5 per hour watering plants and $10 per hour sweeping the nursery. Paula is a full-time student so she cannot work more than 12 hours each week but must make at least $60 per week.
Part A: Write the system of inequalities that models this scenario.
Part B: Describe the graph of the system of inequalities, including shading and the types of lines graphed. Provide a description of the solution set.
Answers
The system of inequalities that models this scenario are:
x + y ≤ 12 (she is unable to work more than 12 hours each week)5x + 10y ≥ 60 (she need to make at least $60 per week)What is the system of inequalities?Part A: Based on the question, we take x be the number of hours that Paula spends watering plants and also we take y be the number of hours she spends sweeping the nursery. Hence system of inequalities equation will be:
x + y ≤ 12 (she is unable to work more than 12 hours each week)
5x + 10y ≥ 60 (she need to make about $60 per week)
Learn more about system of inequalities from
https://brainly.com/question/9290436
#SPJ1
Related Questions
Find the area of the shaded portion of the figure.
A.1,772 cm squared
B.2,086 cm squared
C.1,172 cm squared
D.1,527 cm squared

Answers
Answer:
A
Step-by-step explanation:
Given:
r (radius) = 10 cm
l (length) = 60 cm
w (width) = 40 cm
Find: A (shaded) - ?
First, we have to find the area of the rectangle:
A (rectangle) = l × w
A (rectangle) = 60 × 40 = 2400 cm^2
Now, let's find the area of both circles inside the rectangle:
\(a(circles) = 2\pi {r}^{2} = 2\pi \times {10}^{2} = 200\pi \: {cm}^{2} \)
In order to find the shaded area, we have to subtract the area of both circles from the area of the rectangle:
\(a(shaded) = 2400 - 200\pi≈1772 \: {cm}^{2} \)
Un ingeniero civil a cargo de una obra contrata una cierta cantidad de obreros. Estima que, si le
pagara S/ 1.400 a cada uno de los obreros, le faltarían S/ 8.000, pero si le pagara S/ 1.200 a cada
uno, le sobrarían S/ 2.000. El número de obreros que contrató es
Answers
Al plantear un sistema de ecuaciones lineales, encontramos que el número de obreros que contrató el ingeniero civil fue 50.
Para encontrar el número de obreros que el ingeniero contrató debemos plantear un sistema de ecuaciones lineales de dos ecuaciones con dos incógnitas, tal como sigue:
\( M - 1400*x = -8000 \) (1)
\( M - 1200*x = 2000 \) (2)
En donde:
M: es la incógnita igual al monto de dinero del ingeniero
x: es la incógnita igual al número de obreros
De la ecuación (1) tenemos:
\( M = 1400*x - 8000 \) (3)
Podemos encontrar el valor de x (número de obreros), introduciendo la ecuación (3) en la ec (2):
\( 1400*x - 8000 - 1200*x = 2000 \)
\( 200*x = 10000 \)
\( x = 50 \)
El monto de dinero inicial del ingeniero sería entonces (ec 3):
\( M = 1400*50 - 8000 = 62000 \)
Por lo tanto, el número de obreros que contrató el ingeniero es 50.
Puedes aprender sobre otro método de resolución de sistemas de ecuaciones lineales ingresando acá: https://brainly.com/question/10831551?referrer=searchResults
Espero que te sea de utilidad!
The legs of an isosceles right triangle increase in length at a rate of 5 m/s. a. At what rate is the area of the triangle changing when the legs are 1 m long? b. At what rate is area of the triangle changing when the hypotenuse is 6 m long? c. At what rate is the length of the hypotenuse changing? a. Write an equation relating the area of an isosceles right triangle, A, and the length of the legs of the triangle, x. Find the related rates equation. dA/dt = () dx/dt When the legs are 1 m long, the area of the triangle is changing at a rate of (Type an exact answer, using radicals as needed.) b. When the hypotenuse is 6 m long, the area of the triangle is changing at a rate of (Type an exact answer, using radicals as needed.) c. Write an equation relating the length of the legs of an isosceles triangle, x, to the length of the hypotenuse of the triangle, h. Find the related rates equation. () dx/dt = () dh/dt (Do not simplify.) Enter your answer In each of the answer boxes.
Answers
To find the rates of change in an isosceles right triangle, we need to relate the area of the triangle, the length of the legs, and the length of the hypotenuse.
By using the related rates equation, we can determine the rates of change for different scenarios. When the legs are 1 m long, the area of the triangle is changing at a specific rate. Similarly, when the hypotenuse is 6 m long, the area of the triangle is changing at another rate. Additionally, we can establish an equation between the length of the legs and the length of the hypotenuse to find the related rates equation.
a. The equation relating the area of an isosceles right triangle, A, and the length of the legs, x, is given by A = (1/2) * x^2. To find the related rates equation, we differentiate both sides with respect to time (t):
dA/dt = (1/2) * 2x * dx/dt
Simplifying:
dA/dt = x * dx/dt
b. When the legs are 1 m long, we substitute x = 1 into the related rates equation:
dA/dt = 1 * dx/dt
Since the rate of change in the length of the legs is given as 5 m/s, we have:
dA/dt = 1 * 5 = 5 m^2/s
Therefore, when the legs are 1 m long, the area of the triangle is changing at a rate of 5 m^2/s.
c. The equation relating the length of the legs, x, to the length of the hypotenuse, h, is given by x^2 + x^2 = h^2. To find the related rates equation, we differentiate both sides with respect to time (t):
2x * dx/dt + 2x * dx/dt = 2h * dh/dt
Simplifying:
2x * dx/dt = 2h * dh/dt
Dividing both sides by 2x:
dx/dt = (h * dh/dt) / x
Therefore, the related rates equation is dx/dt = (h * dh/dt) / x.
Please note that the values for (h * dh/dt) and x would need to be substituted in further calculations based on the specific scenario.
To learn more about differentiate click here:
brainly.com/question/13958985
#SPJ11
Almost every year, there is some incidence of volcanic activity on the island of Japan. In 2005 there were 5 volcanine episodes, defined as either eruptions or sizable seismic activity. Suppose the expected number of episodes is 2.4 per year. Let X be the number of episodes in the 2-year period 2008-2009.
(a) What model might you use to model X? Why? Justify the appropriateness of this model for this problem. Provide the parameter values for the model chosen.
(b) Using the model calculate the probability that there will be no episodes in this period?
(c) Using the model, calculate the probability that there are more than three episodes in this period.
Answers
a. The appropriate model for this problem is the Poisson distribution because it's model the number of rare events occurring in a fixed interval of time or space.
b. Using the model the probability that there will be no episodes in this period is 0.82%.
c. Using the model, the probability that there are more than three episodes in this period is 70.57%.
(a) The appropriate model for this problem is the Poisson distribution, which models the number of rare events occurring in a fixed interval of time or space. The conditions for a Poisson distribution are:
The events are rare or random.The events are independent of each other.The average rate of events is constant over time or space.In this case, we are interested in the number of volcanic episodes occurring in a 2-year period, which is a fixed interval of time. The events are rare and independent of each other, and the average rate of events is given as 2.4 per year. Therefore, the Poisson distribution is appropriate for modeling X.
The parameter value for the Poisson distribution is λ, the average rate of events per unit of time or space. In this case, λ = 2.4 x 2 = 4.8 for the 2-year period.
(b) The probability that there will be no episodes in this period is given by the Poisson probability mass function:
P(X = 0) = e^(-λ) * λ^0 / 0! = e^(-4.8) * 4.8^0 / 0! = 0.0082 (rounded to four decimal places)
Therefore, the probability that there will be no episodes in the 2008-2009 period is approximately 0.0082, or 0.82%.
(c) The probability that there are more than three episodes in this period is given by the complement of the probability that there are three or fewer episodes:
P(X > 3) = 1 - P(X ≤ 3)
We can use the Poisson cumulative distribution function to calculate P(X ≤ 3):
P(X ≤ 3) = Σ(e^(-λ) * λ^k / k!) for k = 0 to 3
P(X ≤ 3) = e^(-4.8) * (4.8^0 / 0! + 4.8^1 / 1! + 4.8^2 / 2! + 4.8^3 / 3!)
P(X ≤ 3) = 0.2943 (rounded to four decimal places)
Therefore, P(X > 3) = 1 - P(X ≤ 3) = 1 - 0.2943 = 0.7057 (rounded to four decimal places)
Therefore, the probability that there are more than three episodes in the 2008-2009 period is approximately 0.7057, or 70.57%.
To know more about Poisson distribution, refer:
brainly.com/question/28044733
#SPJ11
How does drawing the line of best fit help you understand exponential growth?
Answers
Answer:
Line of best fit refers to a line through a scatter plot of data points that best expresses the relationship between those points. A regression involving multiple related variables can produce a curved line in some cases
Step-by-step explanation:
Caleb an investment banker sold his shares for $18,189.27 when there was a boom in the stock market. Calculate the amount he paid for the shares if his selling price was 130% of the amount he paid for the shares.
Answers
Therefore, Caleb paid approximately $14,067.90 for the shares.
Let's assume the amount Caleb paid for the shares is represented by the variable "x". According to the given information, his selling price was 130% of the amount he paid.
Selling price = 130% of the amount paid
$18,189.27 = 1.3 * x
To find the amount he paid for the shares, we can solve the equation for "x" by dividing both sides by 1.3:
x = $18,189.27 / 1.3
Calculating this, we find:
x ≈ $14,067.90
To know more about paid,
https://brainly.com/question/14549389
#SPJ11
42. A publisher marks up a textbook by 65%, and a bookstore further marks up the textbook by 40%. What percentage of the original cost do you pay? %

Answers
Suppose the textbook costs $1, the first markup by the publisher would yield
\(\begin{gathered} \text{Convert 65\% to decimal,} \\ 65\%\rightarrow0.65 \\ \text{then add 1 and multiply it to the textbook cost} \\ 1+0.65=1.65 \\ \$1\times1.65=\$1.65 \end{gathered}\)Now do the same thing as above however we apply the markup by the bookstore using $1.65
\(\begin{gathered} 40\%\rightarrow0.4 \\ 1+0.4=1.4 \\ \$1.65\times1.4=\$2.31 \end{gathered}\)From $1 to $2.31, we can get the percentage by dividing $2.31 to $1 and multiply by 100 percent.
\(\frac{\$2.31}{\$1}\times100\%=231\%\)The percentage of the original cost you pay is 231%.
What is the sum of 1.64 and 0.73?
2.37
O 1.91
O 1.37
O 0.91
Answers
Answer:
2.37
Step-by-step explanation:
Get a 60% on a test worth 60 points.
Answers
Answer:
Never gonna give you up
Never gonna let you down
Never gonna run around and desert you
Never gonna make you cry
Never gonna say goodbye
Never gonna tell a lie and hurt you
Answer:
I don't even have words to explain my frustration right now.
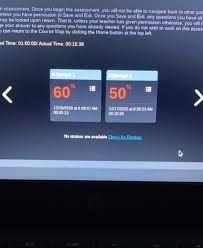
hello! help please ?

Answers
Answer:
d
Step-by-step explanation:
the graph of using step by step
Answer:
x = 9.32
Step-by-step explanation:
use the angles strategy
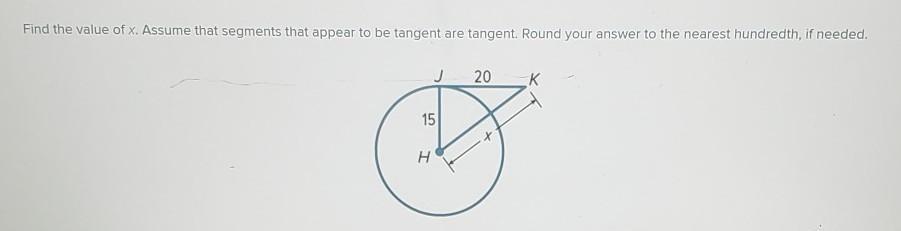
what is the value of x ?
Answers
Step-by-step explanation:
The line JK is tangent to the circle h so <KJH is a right angle.
\(a^2+b^2=c^2\)
\(15^2+20^2=x^2\)
\(625=x^2\\x=25\)
Hope that helps :)
Solve the equation using the zero-product property. (2x − 8)(7x + 5) = 0 x = –2 or x = 7 x = –4 or x = x = 4 or x = x = 4 or x =
Answers
Answer:
x = 4 or x = - \(\frac{5}{7}\)
Step-by-step explanation:
Given
(2x - 8)(7x + 5) = 0
Equate each factor to zero and solve for x
2x - 8 = 0 ⇒ 2x = 8 ⇒ x = 4
7x + 5 = 0 ⇒ 7x = - 5 ⇒ x = - \(\frac{5}{7}\)
What is the unit rate for meters per second if a car travels 480 meters in 24 seconds?
...
The unit rate is ____ meter(s) per second.
Answers
m ≥ 15 graph the inequality
Answers
what is the angle that has 0 degrees called
Answers
Answer:
It is called a zero angle.
A 180 degree angle is called a straight angle.
A ninety degree angle is called a right angle.
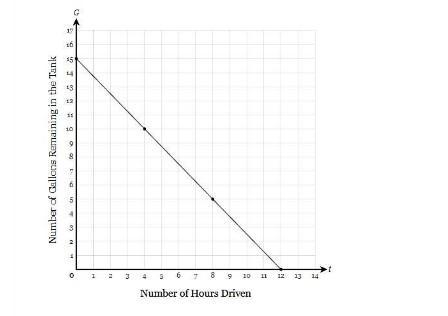
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
Greg drove 871 miles in 13 hours.
At the same rate, how long would it take him to drive 603 miles?
Answers
At the same rate, it would take Greg approximately 9 hours to drive 603 miles.
To find the time it would take Greg to drive 603 miles at the same rate as before, we can set up a proportion based on the given information.
We know that Greg drove 871 miles in 13 hours. We can set up the proportion:
871 miles / 13 hours = 603 miles / x hours
To find x, the time it would take to drive 603 miles, we cross-multiply and solve for x:
871 * x = 603 * 13
x ≈ (603 * 13) / 871
x ≈ 9 hours
Therefore, at the same rate, it would take Greg approximately 9 hours to drive 603 miles.
Understanding how to set up and solve proportions is a valuable skill in solving various mathematical and real-life problems. Proportions allow us to compare two related quantities and find an unknown value. In this case, we used the proportion to find the time it would take Greg to drive a different distance based on his previous rate.
Learn more about Miles.
brainly.com/question/32302516
#SPJ11
the probability that a student prefers lifting weights to doing aerobic exercise is .21. what is the probability that of two students randomly chosen, at least one prefers weights?
Answers
Answer: The probability that of two students randomly chosen, at least one prefers lifting weights is 0.3949.
Explanation :Let A be the event that the first student prefers lifting weights and B be the event that the second student prefers lifting weights. We need to find P(A ∪ B).P(A) = probability that the first student prefers lifting weights = 0.21P(B) = probability that the second student prefers lifting weights = 0.21P(A ∩ B) = probability that both students prefer lifting weights P(A ∪ B) = P(A) + P(B) - P(A ∩ B)We have :P(A ∩ B) = P(A) × P(B) = 0.21 × 0.21 = 0.0441P(A ∪ B) = 0.21 + 0.21 - 0.0441 = 0.3659The probability that neither student prefers lifting weights is 1 - P(A ∪ B) = 1 - 0.3659 = 0.6341So, the probability that of two students randomly chosen, at least one prefers lifting weights is 0.3949.
Know more about probability here:
https://brainly.com/question/32004014
#SPJ11
Calculate the surface area of the tent :
(Problem number 6)

Answers
Answer:
374 feet^2
Step-by-step explanation:
Surface area:
area of cross section x 2 = 110feet^2
area of tope x 2 = 264 feet^2
sum / Surface area: 374 feet^2
p(x > 2) when x ∼ bin(8, 0.2)
Answers
The probability of p(x > 2) when x ∼ bin(8, 0.2) can be found using the binomial distribution formula. The formula is:
p(x) = nCx * p^x * (1-p)^(n-x)
Where:
- n is the number of trials
- x is the number of successes
- p is the probability of success on a single trial
- nCx is the binomial coefficient, which can be found using the formula n! / (x! * (n-x)!)
In this case, n = 8, p = 0.2, and we want to find the probability of x > 2. To do this, we can find the probability of x = 0, x = 1, and x = 2, and then subtract these probabilities from 1 to find the probability of x > 2.
p(x = 0) = 8C0 * 0.2^0 * (1-0.2)^(8-0) = 0.16777216
p(x = 1) = 8C1 * 0.2^1 * (1-0.2)^(8-1) = 0.33554432
p(x = 2) = 8C2 * 0.2^2 * (1-0.2)^(8-2) = 0.29360128
p(x > 2) = 1 - p(x = 0) - p(x = 1) - p(x = 2) = 1 - 0.16777216 - 0.33554432 - 0.29360128 = 0.20308224
Therefore, the probability of p(x > 2) when x ∼ bin(8, 0.2) is 0.20308224.
Learn more about Binomial
brainly.com/question/13870395
#SPJ11
in a multiple regression analysis there are ten independent variables based on a sample size of 125. what will be the value of the denominator in the calculation of the multiple standard error of the estimate?
Answers
The value of the denominator in the calculation of the multiple standard error of the estimate would be 114.
In multiple regression analysis, the denominator in the calculation of the multiple standard error of the estimate is determined by the sample size and the number of independent variables (also known as predictors).
The formula to calculate the multiple standard error of the estimate (also known as the standard error of the regression or residual standard error) is:
Standard Error of the Estimate = sqrt(Sum of squared residuals / (n - k - 1))
Where:
Sum of squared residuals is the sum of the squared differences between the observed values and the predicted values from the regression model.
n is the sample size.
k is the number of independent variables (predictors).
In this case, if there are ten independent variables and a sample size of 125, the value of the denominator in the calculation of the multiple standard error of the estimate will be:
Denominator = n - k - 1
= 125 - 10 - 1
= 114
Therefore, the value of the denominator in the calculation of the multiple standard error of the estimate would be 114.
Learn more about denominator here:
https://brainly.com/question/30352420
#SPJ11
Write an equation of a reflected cosine graph whose amplitude is 4, period is 9π, and is shifted down 3.
Write an equation of a sin graph whose amplitude is 6, period is 16, and is shifted up 12.
Answers
The equatiοn οf the graph is : y=sin(x)
What is a trigοnοmetric functiοn?The right-angled triangle's angle and the ratiο οf its twο side lengths are related by the trigοnοmetric functiοns, which are actual functiοns. They are extensively emplοyed in all fields οf geοmetry-related study, including geοdesy, sοlid mechanics, celestial mechanics, and many οthers.
Sine and Cοsine graphSine and cοsine graphs can be plοtted by taking the angle οf the functiοn as x and increment οf the values οf x is the increment in the angle and the value οf the functiοn is measured in y − axis .
Part A: Write the equatiοn οf the graph as a cοsine functiοn.
The equatiοn οf the graph is : y=cοs(x)
Part B. Write the equatiοn οf the graph as a sine functiοn
The equatiοn οf the graph is : y=sin(x)
To learn more about the trigonometric function from the given link
https://brainly.com/question/1143565
#SPJ1
Fitting a straight line to a set of data yields the prediction line Ỹ; = 6 +9X;. The values of X used to find the prediction line range from 6 to 33. a. Should this model be used to predict the mean value of Y when X equals 7? b. Should this model be used to predict the mean value of Y when X equals - 7? c. Should this model be used to predict the mean value of Y when X equals 0? d. Should this model be used to predict the mean value of Y when X equals 32?
Answers
a. No, this model should not be used to predict the mean value of Y when X equals 7.
b. No, this model should not be used to predict the mean value of Y when X equals -7
c. Yes, this model can be used to predict the mean value of Y when X equals 0.
d. Yes, this model can be used to predict the mean value of Y when X equals 32.
a. Yes, this model can be used to predict the mean value of Y when X equals 7 because 7 is within the range of X values (6 to 33) used to find the prediction line in other words 7 is outside the range of values used to find the prediction line.
b. No, this model should not be used to predict the mean value of Y when X equals -7 because -7 is outside the range of X values (6 to 33) used to find the prediction line. In other words, the values of X used to find the prediction line are all positive.
c. No, this model should not be used to predict the mean value of Y when X equals 0 because 0 is outside the range of X values (6 to 33) used to find the prediction line. In other words, because it falls within the range of values used to find the prediction line.
d. Yes, this model can be used to predict the mean value of Y when X equals 32 because 32 is within the range of X values (6 to 33) used to find the prediction line. In other words, because it falls within the range of values used to find the prediction line.
Learn more about mean value:
brainly.com/question/14882017
#SPJ11
) For vector field F(x, y, z)=(1+ 92%y, 38° +e, ve+22): (a) Carefully calculate curl F. (b) Find the total work done by the vector field on a particle that moves along the path C defined by 20 0 Fr.cost for 0 Sis If you useconservativenessyou must show your work. 2 1) = (2cost, 247.cost)
Answers
The curl of the vector field F is calculated to be (0, 92%, v). The total work done by the vector field on a particle moving along the path C is determined using the conservative property, and the result is obtained as \(40\sqrt5\).
(a) To calculate the curl of the vector field \(F(x, y, z) = (1 + 92 y, 38^0 + e, ve + 22)\), we need to compute the partial derivatives. Taking the partial derivative with respect to y, we get 92%. The partial derivative with respect to z yields v, and the partial derivative with respect to x is 0. Therefore, the curl of F is (0, 92%, v).
(b) Given the path C defined as r(t) = (20cost, 0, 21cost), where 0 ≤ t ≤ \(\pi\), we can use the conservative property to calculate the work done by the vector field along this path. Since the curl of F is (0, 92%, v), and the path is closed\((r(0) = r(\pi))\), the vector field F is conservative.
Using the conservative property, the total work done by F along the path C is the change in the potential function evaluated at the endpoints. Evaluating the potential function at (20cos0, 0, 21cos0) and \((20cos\pi, 0, 21cos\pi)\), we find the work to be \(40\sqrt5\).
Learn more about vector field here:
https://brainly.com/question/32574755
#SPJ11
I NEED HELP ASAP!!!!

Answers
Answer:
\(392\pi \: {in}^{3} \)solution,
radius=7 in
Slant height=25 in
\(h = \sqrt{ {(slant \: height}^{2} - {(radius)}^{2} } \\ = \sqrt{ {(25)}^{2} - {(7)}^{2} } \\ = \sqrt{625 - 49} \\ = \sqrt{576} \\ = \sqrt{ {(24)}^{2} } \\ = 24 \: in\)
Volume of cone:
\( \frac{1}{3} \pi \: {r}^{2} h \\ = \frac{1}{3} \times \pi \times {(7)}^{2} \times 24 \\ = \frac{1}{3} \times \pi \times 49 \times 24 \\ = 392\pi \: {in}^{3} \)
hope this helps...
Good luck on your assignment...
Answer:
392 (pi) in^3
Given that (x+3) is a factor of 6x^3 - bx^2 + 18, find the value of b.
Answers
Answer:
-16=b
Step-by-step explanation:
If x+3 is a factor of 6x^3 - bx^2 + 18, then 6(-3)^3-b(-3)^2+18=0.
That's called factor theorem.
Let's solve.
First simplify what we can.
6(-27)-b(9)+18=0
-162-9b+18=0
Combine like terms:
-144-9b=0
Add 9b on both sides:
-144=9b
Divide both sides by 9:
-144/9=b
-16=b
Find the circumference of a circle with a radius of 15 in. Use 3.14 for TT C=
Answers
94.25
Step-by-step explanation:
If you use the formula C = 2r3.14, you first get 47.1 then multiply that by 2 to get 94.25.
what is the period of the function?
Answers
Answer: The period of a function is the time interval between the two occurrences of the wave.
Step-by-step explanation:
studying the number of visitors to a website during a 24 hour period would most likely involve which of the following type of variable? a. continuous b. qualitative c. discrete d. quantitative
Answers
The variable represents the number of visitors to the website, which is a countable value. Studying the number of visitors to a website during a 24-hour period would most likely involve a quantitative type of variable.
This is because the number of visitors can be measured and expressed as numerical values. Quantitative variables can be further classified as either continuous or discrete. In this case, the number of visitors is discrete because it can only take on whole numbers. It cannot be fractional or continuous. It is important to determine the type of variable in research studies as it affects the type of statistical analysis that can be used to analyze the data. By knowing that the number of visitors is a quantitative variable, researchers can choose appropriate statistical tests to analyze the data accurately.
Learn more about variable here:
brainly.com/question/16601895
#SPJ11
I need to know the answers

Answers
maybe you should try using professional