Answers
Explanation:
1) x^3-5x^2+7x-12/x-4
2) x^3-4x-x^2+4x+3x-12/x-4
3) x^2x(x-4)-x*(x-4)+3(x-4)/x-4
4) x^2-x*3 because x-4 cancels each other out
9514 1404 393
Answer:
x^2 -x +3
Step-by-step explanation:
The long division is shown in the attachment, along with details of how the quotient terms are found.
\(\dfrac{x^3-5x^2+7x-12}{x-4}=\boxed{x^2-x+3}\)

Related Questions
what is the sum of the 3rd and 5th square numbers????
Answers
Answer:
40
Step-by-step explanation:
as 1st sq no is.4 and 2nd sq no. is 36
and their sum is =4+36
=40.....ans
Which is an equation of the line with a slope of 2 that passes through (3,−5)?
Answers
Answer: \(y=2x-11\)
Step-by-step explanation:
Given
The line has a slope of 2 and passes through (3,-5)
Using slope point form that is
\(\Rightarrow \dfrac{y-y_1}{x-x_1}=m\)
Insert values
\(\Rightarrow \dfrac{y-(-5)}{x-3}=2\\\\\Rightarrow y+5=2x-6\\\Rightarrow y=2x-11\ or\ 2x-y=11\)
NO LINKS!!! URGENT HELP PLEASE!!!
State if the given functions are inverses.
1. g(x) = 4 + (7/2)x
f(x) = 5 - (4/5)x
Find the inverses of each function.
2. g(n) = (8/3)n + 7/3
3. g(x) = 1 - 2x^3
Answers
Answer:
1) The functions are not inverses.
\(\textsf{2)} \quad g^{-1}(n)=&\dfrac{3}{8}n-\dfrac{7}{8}\)
\(\textsf{3)} \quad g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\)
Step-by-step explanation:
Question 1The inverse composition rule states that if two functions are inverses of each other, then their compositions result in the identity function.
Given functions:
\(g(x) = 4 + \dfrac{7}{2}x \qquad \qquad f(x) = 5 - \dfrac{4}{5}x\)
Find g(f(x)) and f(g(x)):
\(\begin{aligned} g(f(x))&=4+\dfrac{7}{2}f(x)\\\\&=4+\dfrac{7}{2}\left(5 - \dfrac{4}{5}x\right)\\\\&=4+\dfrac{35}{2}-\dfrac{14}{5}x\\\\&=\dfrac{43}{2}-\dfrac{14}{5}x\\\\\end{aligned}\) \(\begin{aligned} f(g(x))&=5 - \dfrac{4}{5}g(x)\\\\&=5 - \dfrac{4}{5}\left(4 + \dfrac{7}{2}x \right)\\\\&=5-\dfrac{16}{5}-\dfrac{14}{5}x\\\\&=\dfrac{9}{5}-\dfrac{14}{5}x\end{aligned}\)
As g(f(x)) or f(g(x)) is not equal to x, then f and g cannot be inverses.
\(\hrulefill\)
Question 2To find the inverse of a function, swap the dependent and independent variables, and solve for the new dependent variable.
Calculate the inverse of g(n):
\(\begin{aligned}y &= \dfrac{8}{3}n + \dfrac{7}{3}\\\\n &= \dfrac{8}{3}y + \dfrac{7}{3}\\\\3n &= 8y + 7\\\\3n-7 &= 8y\\\\y&=\dfrac{3}{8}n-\dfrac{7}{8}\\\\g^{-1}(n)&=\dfrac{3}{8}n-\dfrac{7}{8}\end{aligned}\)
Calculate the inverse of g(x):
\(\begin{aligned}y &= 1-2x^3\\\\x &= 1-2y^3\\\\x -1&=-2y^3\\\\2y^3&=1-x\\\\y^3&=\dfrac{1}{2}-\dfrac{1}{2}x\\\\y&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\\end{aligned}\)
Answer:
1.
If the composition of two functions is the identity function, then the two functions are inverses. In other words, if f(g(x)) = x and g(f(x)) = x, then f and g are inverses.
For\(\bold{g(x) = 4 + \frac{7}{2}x\: and \:f(x) = 5 -\frac{4}{5}x}\), we have:
\(f(g(x)) = 5 - \frac{4}{5}(4 + \frac{7}{2}x)\\ =5 - \frac{4}{5}(\frac{8+7x}{2})\\=5 - \frac{2}{5}(8+7x)\\=\frac{25-16-14x}{5}\\=\frac{9-14x}{5}\)
\(g(f(x)) = 4 + (\frac{7}{5})(5 - \frac{4}{5}x) \\=4 + (\frac{7}{5})(\frac{25-4x}{5})\\=4+ \frac{175-28x}{25}\\=\frac{100+175-28x}{25}\\=\frac{175-28x}{25}\)
As you can see, f(g(x)) does not equal x, and g(f(x)) does not equal x. Therefore, g(x) and f(x) are not inverses.
Sure, here are the inverses of the functions you provided:
2. g(n) = (8/3)n + 7/3
we can swap the roles of x and y and solve for y to find the inverse of g(n). In other words, we can write the equation as y = (8/3)n + 7/3 and solve for n.
y = (8/3)n + 7/3
n =3/8*( y-7/3)
Therefore, the inverse of g(n) is:
\(g^{-1}(n) = \frac{3}{8}(n - \frac{7}{3})=\frac{3}{8}*\frac{3n-7}{3}=\boxed{\frac{3n-7}{8}}\)
3. g(x) = 1 - 2x^3
We can use the method of substitution to find the inverse of g(x). We can substitute y for g(x) and solve for x.
\(y = 1 - 2x^3\\2x^3 = 1 - y\\x = \sqrt[3]{\frac{1 - y}{2}}\)
Therefore, the inverse of g(x) is:
\(g^{-1}(x) =\boxed{ \sqrt[3]{\frac{1 - x}{2}}}\)
Translate 2 3 y − 9 < y + 1 into a sentence. Nine than two-thirds of number is less than the number .
Answers
The sentence translation of "2/3y - 9 < y + 1" is "Nine less than two-thirds of a number is less than the number."
To translate the inequality expression "2/3y - 9 < y + 1" into a sentence, we can break it down into smaller parts:
"2/3y" represents two-thirds of a number.
"9" represents the number nine.
"y + 1" represents the number increased by one.
Now let's construct the sentence:
"Nine less than two-thirds of a number" - This refers to the expression "2/3y - 9," indicating that we have subtracted nine from two-thirds of a number.
"is less than" - This is the comparison symbol in the inequality.
"the number" - This refers to the expression "y + 1," representing the number increased by one.
Combining these parts, we form the sentence: "Nine less than two-thirds of a number is less than the number."
Hence, the correct sentence translation of "2/3y - 9 < y + 1" is "Nine less than two-thirds of a number is less than the number."
For more such questions on sentence translation, click on:
https://brainly.com/question/28958546
#SPJ8
When converted to a household measurement, 9 kilograms is approximately equal to a
Answers
Answer:
D) 19.8 lbs
Explanation:
1kg in household measurement is equal to 35.274 ounces. 35.274*9=317.466 ounces.
1kg is also equal to 2.205 lbs. 9*2.205=19.8416
9 kg is also equal to 9000 grams, but grams are not a part of the household measurement system
a) 9000 grams. b) 9000 ounces. c) 19.8 ounces. d) 19.8 pounds.
This leaves us with 19.8 lbs
How is multiplying 3/9 and 6/9 different from adding the two fractions
Answers
By multiplying the two fractions we get 2 / 9, and by adding we get 1.
In arithmetic, a product is the result of multiplication or an expression that identifies elements to be improved.
In math, multiply the method to add equal corporations. Whilst we multiply, the range of factors in the institution will increase. the two factors and the product are parts of a multiplication problem. Within the multiplication trouble, 6 × 9 = 54, the numbers 6 and 9 are the factors, at the same time as the range 54 is the product.
Multiplication is defined as calculating the end result of repeated additions of two numbers. An instance of multiplication is 4 instances 2 equals 8.
By multiplying the two fractions,
= 3 / 9 * 6 / 9
= 2 / 9
By adding the two fractions,
= 3 / 9 + 6 / 9
= 9 / 9
= 1
Learn more about multiplication here https://brainly.com/question/10873737
#SPJ9
PLEASE HELP ME!! I WILL GIVE YOU BRAINLIST!!!!

Answers
Answer: it should be C.
Step-by-step explanation: because its ascking to describe the formation.
If someone can do this with in next hour and half before its due that would be awesome!!!

Answers
g(x, y) = √(16 - x² - y²)
(a) what is the domain of g?
b) what is the total differential g
Answers
(a) The domain of g(x, y) is the disk D = {(x, y) : x² + y² ≤ 16}.
(b) The total differential of g is dg = -x/(√(16 - x² - y²))dx - y/(√(16 - x² - y²))dy.
What is the domain of the function?The domain of g(x, y) is the set of all values of x and y that satisfy the condition inside the square root to be non-negative.
16 - x² - y² ≥ 0
- x² - y² ≥ -16
x² + y² ≤ 16
The total differential dg of g(x, y), is calculated as follows;
dg = (∂g/∂x)dx + (∂g/∂y)dy
Using the chain rule, we have;
∂g/∂x = (1/2)(16 - x² - y²)^(-1/2)(-2x)
∂g/∂x = -x/(√(16 - x² - y²))
∂g/∂y = (1/2)(16 - x² - y²)^(-1/2)(-2y)
∂g/∂y = -y/(√(16 - x² - y²))
dg = -x/(√(16 - x² - y²))dx - y/(√(16 - x² - y²))dy.
Learn more about domain of functions here: https://brainly.com/question/28934802
#SPJ1
Since my uncles farmyeard apperas to be overrun with gos and chickens i asked him hom many of each did he have he responded that his dog and chicked had a total of 148 legs and 60 heads. hime mmay of each does he have
Answers
There are 14 dogs and 46 chickens in the farmyard.
The supposition that there are d dogs and c chickens.
Each chicken has two legs, but each dog has four.
Consequently, the total number of legs may be written as follows:
4d + 2c
Since we are aware that there are 148 legs in total, we can construct the following equation:
4d + 2c = 148
We may create another equation since we know that there are a total of 60 heads (dogs and chickens):
d + c = 60
Now that we have two equations with two variables, we may answer them both at the same time.
2d + 2c = 120 is the result of multiplying the second equation by two.
When we deduct this from the first equation, we obtain 2d = 28.
So, d = 14.
Reintroducing this into the second equation, we get:
14 + c = 60
So, c = 46.
For similar questions on farmyard
https://brainly.com/question/772512
#SPJ11
What is the domain of the square root function graphed below?
On a coordinate plane, a curve open up to the right in quadrant 4. It starts at (0, negative 1) and goes through (1, negative 2) and (4, negative 3).
x less-than-or-equal-to negative 1
x greater-than-or-equal-to negative 1
x less-than-or-equal-to 0
x greater-than-or-equal-to 0
Mark this and return
Answers
The domain of the square root function is x greater-than-or-equal-to 0, since the function is defined for all non-negative x-values or x-values greater than or equal to zero.
The domain of the square root function graphed below can be determined by looking at the x-values of the points on the graph.
From the given information, we can see that the curve starts at (0, -1) and goes through (1, -2) and (4, -3).
The x-values of these points are 0, 1, and 4.
Since the square root function is defined for any non-negative x-values or x-values more than or equal to zero, its domain is x greater-than-or-equal-to 0.
for such more question on domain
https://brainly.com/question/16444481
#SPJ8
one and three fifths plus three and two thirds equals blank
Answers
Answer: 5 4/15
Step-by-step explanation:
1 3/5 + 3 2/3 = 8/5 + 11/3
Find the common denominator (5 and 3) = 15
So 8/5 equals to 24/15 because if 5 x 3 = 15 , 8 must also multiply by 3.
11/3 equals to 55/15 because if 3 x 5 = 15 , 11 must also multiply by 5.
Thus 24/15 + 55/15 = 79/15
This is an improper fraction, so converting to mixed number:
79/15 = 5 4/15 because 5 x 15 + 4 = 79
Which set of numbers can represent the side lengths, in centimeters, of a right triangle?
Answers
A set of numbers that can represent the side lengths, in centimeters, of a right triangle is any set that satisfies the Pythagorean theorem, where the square of the hypotenuse's length is equal to the sum of the squares of the other two sides.
A right triangle is a type of triangle that contains a 90-degree angle. According to the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Let's consider a set of numbers that could represent the side lengths of a right triangle in centimeters.
One possible set could be 3 cm, 4 cm, and 5 cm.
To verify if this set forms a right triangle, we can apply the Pythagorean theorem.
Squaring the length of the shortest side, 3 cm, gives us 9. Squaring the length of the other side, 4 cm, gives us 16.
Adding these two values together gives us 25.
Finally, squaring the length of the hypotenuse, 5 cm, also gives us 25. Since both values are equal, this set of side lengths satisfies the Pythagorean theorem, and hence forms a right triangle.
It's worth mentioning that the set of side lengths forming a right triangle is not limited to just 3 cm, 4 cm, and 5 cm.
There are infinitely many such sets that can be generated by using different combinations of positive integers that satisfy the Pythagorean theorem.
These sets are known as Pythagorean triples.
Some other examples include 5 cm, 12 cm, and 13 cm, or 8 cm, 15 cm, and 17 cm.
In summary, a right triangle can have various sets of side lengths in centimeters, as long as they satisfy the Pythagorean theorem, where the square of the hypotenuse's length is equal to the sum of the squares of the other two sides.
For similar question on hypotenuse's.
https://brainly.com/question/30390037
#SPJ8
g A two-factor study with 3 levels of factor A and 3 levels of factor B uses a separate sample of 10 participants in each treatment condition. How many participants are needed for the entire study
Answers
Answer:
the total number of participants required is 90
Step-by-step explanation:
Given the data in the question;
Factor A has three levels
Factor B has three levels
sample size n; ten participants
we have two Way ANOVA involving Factor A and Factor B.
Now,
{ Total # Participants Required } = { #Levels factor A } × { #Levels factor B } × { Sample size of each level }
we substitute
{ Total # Participants Required } = 3 × 3 × 10
{ Total # Participants Required } = 9 × 10
{ Total # Participants Required } = 90
Therefore, the total number of participants required is 90
Find the sum and Express it in simplest form. (u^3+3u^2+3) + (-6u^3-8u^2)
Answers
Answer:
-5u^3 - 5u^2 + 3.
Step-by-step explanation:
(u^3 + 3u^2 + 3) + (-6u^3 - 8u^2)
= u^3 + 3u^2 + 3 - 6u^3 - 8u^2
= u^3 - 6u^3 + 3u^2 - 8u^2 + 3
= -5u^3 - 5u^2 + 3.
Solve for x. x^2 + 4x + 4 = 8
help me out i’ll give you the brainliest! :)

Answers
Lara grows apples in her orchard and sells them at the weekly farmer's market. Each week, she sells the apples for a different price and records the number of apples sold. The scatter plict below
shows the price of one apple and the number of apples that were sold. A line of best fit for these data points, the equation y=-z+32, is also shown on the plot
Apples Number of Apples Sold

Answers
the floor of a rectangular living room is 9 meters by 12 meters. what is the distance between opposite corners of the living room?
Answers
The distance between opposite corners refers to the diagonal, which we can find using Pythagorean's Theorem where the diagonal is the hypotenuse and the given dimensions are the legs.
\(\begin{gathered} c^2=a^2+b^2 \\ c^2=(9m)^2+(12m)^2 \\ c=\sqrt[]{81m^2+144m^2} \\ c=\sqrt[]{225} \\ c=15 \end{gathered}\)Hence, the distance between opposite corners of the living room is 15 meters.Find the answers of both of these

Answers
The volume of the cylinder with a radius of 19 km and a height of 5 km is 5706 km³, using 3.14 for π.
What is the volume of a cylinder?
The cylinder's volume is given by the formula, πr²h, where r is the radius of the circular base and h is the height of the cylinder.
The formula for the volume of a cylinder is given by:
V = π * r²* h
Where r is the radius of the base and h is the height of the cylinder.
Given that the radius of the cylinder is 19 km and the height is 5 km, we can substitute these values into the formula:
V = π * 19² * 5
V = 3.14 * 361 * 5
V = 5706 km³
Therefore, the volume of the cylinder with a radius of 19 km and a height of 5 km is 5706 km³, using 3.14 for π.
To learn more about the volume of a cylinder visit,
https://brainly.com/question/23935577
#SPJ1
Twenty standard cartons of octal boxes weigh a total of 1,100 pounds. Find the weight per carton.
Answers
Twenty standard cartons of octal boxes weigh a total of 1,100 pounds. The weight per carton is 55 pounds.
Given that twenty standard cartons of octal boxes weigh a total of 1,100 pounds. We need to find the weight per carton.
How to find the weight per carton? To find the weight per carton, we need to divide the total weight of twenty standard cartons of octal boxes by 20.Let's assume the weight of each carton be x.
Therefore, the equation can be formed asx * 20 = 1,100 Solving the above equation for x, x = 1,100/20 Therefore, the weight per carton is 55 pounds. So, twenty standard cartons of octal boxes weigh a total of 1,100 pounds.
The weight per carton is 55 pounds.
For more such questions on pounds
https://brainly.com/question/30400939
#SPJ8
A 25-foot ladder leans against a house. The bottom of the ladder is 7 feet from the house.
To the nearest degree, what angle does the ladder make with the ground?
Answers
Answer: it makes 74 degree
Step-by-step explanation: This forms a right triangle. The 25-ft ladder is the hypotenuse of the right triangle. and the 7ft bottom of the ladder is the base of a triangle
For the angle where the ladder meets the ground, the
ground is the adjacent leg. The ladder is the hypotenuse.
Call the angle between the ladder and the ground angle A.
The trig ratio that relates the adjacent leg and the hypotenuse is cosine.
The vertex of this parabola is at (-2, -3). When the x-value is -1, the
y value is -5. What is the coefficient of the squared expression in the
parabola's equation?
(-2,-3)
10

Answers
Step-by-step explanation:
y = a ( x - -2)^2 - 3 <======vertex form of the parabola ...find 'a'
when x = -1 y = -5 sub these into the equation
-5 = a( -1 +2)^2 -3 add 3 to both sides of the equation and simplify
-2 = a
The length of a rectangle is 5 cm more than its width. If the perimeter is 58cm, calculate:
(a) Write an equation to show the perimeter of the rectangle ?
(b) calculate:
I.width
II.length
III. the area of the rectangle
Answers
The equation to show the perimeter of the rectangle is P = 2(2w + 5)
Writing an equation to show the perimeter of the rectangleFrom the question, we have the following parameters that can be used in our computation:
Length = 5 more than the width
Also, we have
Perimeter = 58
This means that
P = 2(w + 5 + w)
P = 2(2w + 5)
Calculating the dimensions and the areaIn (a), we have
P = 2(2w + 5)
This gives
2(2w + 5) = 58
So, we have
2w + 5 = 29
2w = 24
w = 12
Next, we have
l = 12 + 5
l = 17
Lastly, we have
Area = 17 * 12
Area = 204
Read more about area at
https://brainly.com/question/24487155
#SPJ1
Parallelogram JKLM is shown on the coordinate plane below:
Parallelogram JKLM with ordered pairs at J negative 6, 2, at K negative 4, 6, at L negative 3, 3, at M negative 5, negative 1.
If parallelogram JKLM is rotated 270° clockwise around the origin, what are the coordinates of the endpoints of the side congruent to side JM in the image parallelogram?
J′(−2, −6); M′(1, −5)
J′(6, 2); M′(−5, 1)
J′(2, 6); M′(−1, 5)
J′(6, −2); M′(5, 1)
Answers
Answer: Parallelogram JKLM is shown on the coordinate plane below:
Parallelogram JKLM with ordered pairs at J negative 6, 2, at K negative 4, 6, at L negative 3, 3, at M negative 5, negative 1.
If parallelogram JKLM is rotated 270° clockwise around the origin, what are the coordinates of the endpoints of the side congruent to side JM in the image parallelogram?
J′(−2, −6); M′(1, −5)
J′(6, 2); M′(−5, 1)
J′(2, 6); M′(−1, 5)
J′(6, −2); M′(5, 1)
Step-by-step explanation:
A bag contains two red marbles, four green ones, one lavender one, two yellows, and two orange marbles. HINT [See Example 7.] How many sets of five marbles include either the lavender one or exactly one yellow one but not both colors?
Answers
There are 2518 sets of five marbles that include either the lavender one or exactly one yellow one, but not both.
To solve this problem, we need to find the number of sets of five marbles that include either the lavender one or exactly one yellow one, but not both colors. Here's one way to approach the problem:
Number of sets of five marbles that include the lavender one: There is only one lavender marble, so we can choose any 4 other marbles to go with it.
There are a total of 7 marbles to choose from, so there are 7 possible choices for the first marble, 6 for the second, 5 for the third, and 4 for the fourth.
This gives us a total of 7 x 6 x 5 x 4 = 840 possible sets of five marbles that include the lavender one.
Number of sets of five marbles that include exactly one yellow one: There are two yellow marbles,
So there are 2 possible choices for the yellow marble. For each choice, we can choose any 4 other marbles to go with it.
As before, there are 7 marbles to choose from, so there are 7 possible choices for the first marble, 6 for the second, 5 for the third, and 4 for the fourth.
This gives us a total of 2 x (7 x 6 x 5 x 4) = 1680 possible sets of five marbles that include exactly one yellow one.
Number of sets of five marbles that include both the lavender one and exactly one yellow one:
We need to subtract these sets from the total number of sets that include either the lavender one or exactly one yellow one.
We have already found that there are 840 sets of five marbles that include the lavender one, and 1680 that include exactly one yellow one.
To find the number of sets that include both, we can choose any one yellow marble and the lavender one.
There are 2 choices for the yellow marble and 1 choice for the lavender one,
So there are 2 x 1 = 2 possible sets of five marbles that include both the lavender one and exactly one yellow one.
Number of sets of five marbles that include either the lavender one or exactly one yellow one, but not both:
Finally, we need to subtract the number of sets that include both the lavender one and exactly one yellow one from the total number of sets that include either the lavender one or exactly one yellow one.
The total number of sets that include either the lavender one or exactly one yellow one is 840 + 1680 = 2520. The number of sets that include both is 2,
So the number of sets that include either the lavender one or exactly one yellow one, but not both, is 2520 - 2 = 2518.
For more questions on Permutation and Combination
https://brainly.com/question/1216161
#SPJ4
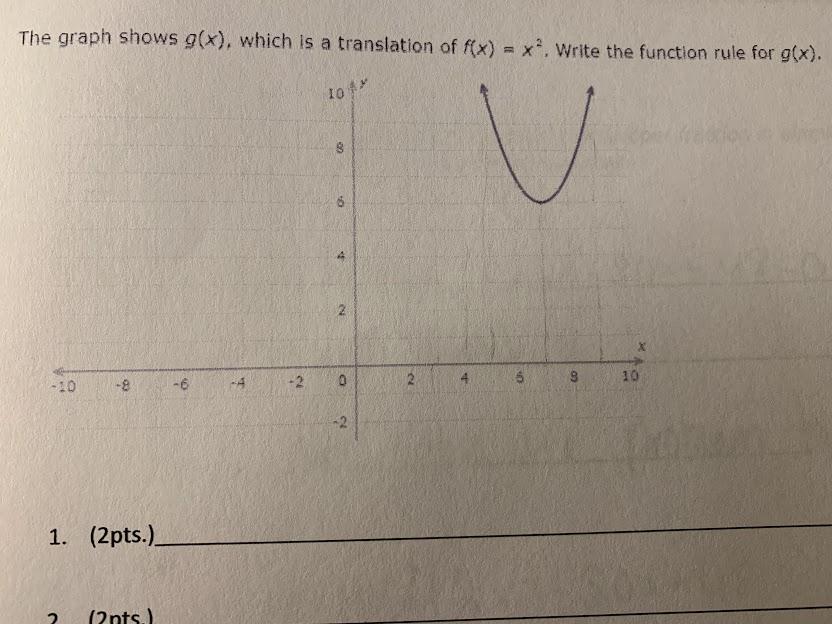
The graph shows g(x), which is a translation of f(x)=x2. Write the function rule for g(x).
Answers
The function rule for g(x) is g(x) = (x - 7)² + 6
How to write the function rule for g(x).From the question, we have the following parameters that can be used in our computation:
The graph
Also, we have
The parent function, f(x) = x²
Using the above (the graph) as a guide, we have the following:
g(x) = f(x - 7) + 6
substitute the known values in the above equation, so, we have the following representation
g(x) = (x - 7)² + 6
Hence, the equation is g(x) = (x - 7)² + 6
Read more about transformation at
https://brainly.com/question/27224272
#SP{J1
What can we do to create more energy?
A: Nothing, energy cannot be created or destroyed
B: destroy old energy and create new energy with power plants
C: Whenever energy changes from one form to another, more energy is created
Answers
To produce more energy, we do energy cannot be generated or destroyed but can only alter its forms.
Energy production and destruction are both possible.Energy can only be changed from one type of energy to another, according to the rule of conservation of energy, and cannot be created or destroyed. Accordingly, until additional energy is added from outside, a system always possesses the same amount of energy.Energy cannot be generated or destroyed but can only alter its forms. It is possible to transfer energy from one system to another, but it is not possible to create energy from scratch. The same holds true for energy; it cannot be destroyed by a system but can be transferred to another.To produce more energy, we do energy cannot be generated or destroyed but can only alter its forms.To learn more about energy refer to:
https://brainly.com/question/13881533
#SPJ1
an art gallery is selling replicas of some famous art work. a copy of the art work is dilated by a scale factor of 1/3 to create a replica of the original piece. if the area of some original artwork was 12 square feet what will be the area of the replica?
Answers
Answer:
4/3 square feet.
Step-by-step explanation:
To find the area of the replica, you need to use a formula that relates the area of the original figure and the area of the dilated figure by the scale factor1. The formula is:
Area of dilated figure = Area of original figure x (Scale factor)^2
In this case, the area of the original artwork is 12 square feet and the scale factor is 1/3. So, we plug these values into the formula and get:
Area of replica = 12 x (1/3)^2
Area of replica = 12 x 1/9
Area of replica = 4/3
So, the area of the replica is 4/3 square feet.
Hope this helps :)
Which expression is equivalent to log Subscript c Baseline StartFraction x squared minus 1 Over 5 x EndFraction?
log Subscript c Baseline x squared minus log Subscript c Baseline 5 x minus 1
2 log Subscript c Baseline x minus (log Subscript c Baseline 5 + log Subscript c Baseline x) minus 1
log Subscript c Baseline (x squared minus 1) minus (log Subscript c Baseline 5 + log Subscript c Baseline x)
2 log Subscript c Baseline x minus log Subscript c Baseline 1 minus log Subscript c Baseline 5 + log Subscript c Baseline x
Answers
The equivalent expression of \(\log_c(\frac{x^2 - 1}{5x})\) is \(\log_c(x^2 - 1) - \log_c(5x)\)
How to determine the equivalent expression?The logarithmic expression is given as:
\(\log_c(\frac{x^2 - 1}{5x})\)
The law of logarithm states that:
log(a) - log(b) = log(a/b)
This means that the expression can be split as:
\(\log_c(\frac{x^2 - 1}{5x}) = \log_c(x^2 - 1) - \log_c(5x)\)
Hence, the equivalent expression of \(\log_c(\frac{x^2 - 1}{5x})\) is \(\log_c(x^2 - 1) - \log_c(5x)\)
Read more about equivalent expression
https://brainly.com/question/2972832
#SPJ1
Terry is the school swimming champion and has won several races. If the ratio of the number of times he's won to the number of races he has swum in is 2 : 3, how many races has he won?
Answers
The given information tells us that Terry's wins-to-races ratio is 2:3, but we cannot determine the exact number of races he has won without additional information about the total number of races he has participated in.
If the ratio of the number of times Terry has won to the number of races he has swum in is 2:3, we can set up a proportion to determine the number of races he has won.
Let's denote the number of times Terry has won as x, and the total number of races he has swum in as y. According to the given ratio, we have:
x/y = 2/3
To find the value of x, we need to solve for x when y is known. Since y represents the total number of races, we don't have that information in the given problem. Therefore, we cannot determine the exact number of races Terry has won without knowing the total number of races he has participated in.
The ratio tells us the relationship between the number of wins and the total number of races, but without knowing the denominator (total races), we cannot find a specific value for the numerator (number of wins). We can only determine the ratio between the two quantities.
for similar questions on races.
https://brainly.com/question/24181944
#SPJ8
