please help as fast as possible!
Classify each pair of labeled angles as complementary, supplementary, or neither.
Drag and drop the choices into the boxes to correctly complete the table. Each pair of angles may belong to more than one category.
complementary
supplementary
neither

Answers
56 and 34 - Complementary
67 and 67 - Supplementary
53 - neither
Related Questions
find the critical points of the functions:
please solve these questions!!
f(x, y) = x² + y2 - 4x + 6y + 2 f(x, y) = x2 + xy + 2y + 2x - 3 f(x, y) = x + y2 + xy f(x, y) = 2x2 + 5xy - y f(x, y) = 3x2 + y2 + 3x - 2y + 3 f(x, y) = x + y2 - 3xy
Answers
To find the critical points of a function, we calculate the partial derivatives and set them equal to zero.
To find the critical points of a function, we need to calculate the partial derivatives with respect to each variable (x and y) and set them equal to zero.
For the function f(x, y) = x² + y² - 4x + 6y + 2:
The partial derivative with respect to x is 2x - 4.
The partial derivative with respect to y is 2y + 6.
Setting these derivatives equal to zero and solving the equations will give us the critical points.
Follow the same steps for the remaining functions: f(x, y) = x² + xy + 2y + 2x - 3, f(x, y) = x + y² + xy, f(x, y) = 2x² + 5xy - y, f(x, y) = 3x² + y² + 3x - 2y + 3, and f(x, y) = x + y² - 3xy.
By solving the resulting equations, we can find the critical points for each function.
To learn more about “derivatives” refer to the https://brainly.com/question/28376218
#SPJ11
How do you write the slope-intercept form of the equation of the line through the given point and parallel to the given line?.
Answers
The slope-intercept form of the equation of the line through the given point and parallel to the given line is y=x−14.
In the given question we have to write the slope-intercept form of the equation of the line through the given point and parallel to the given line.
The given points are (–2, –16).
The given equation of line is y = x – 5.
Standard equation of line is y=mx+c.
After comparing to the standard equation.
Slope m(1) = 1
The line passes through (−2,−16), so the point will satisfy the equation y=mx+c. So
−16=−2*1+c
Simlifying
−16=−2+c
Add 2 on both side, we get
c = −16+2
c = −14
As we know that if line is parallel then
m(1)=m(2)
So the value of solpe m = 1
Now the equation of line
y=1*x+(−14)
y=x−14
To lear more about slope-intercept form of equation link is here
brainly.com/question/21298390
#SPJ4
The right answer is:
How do you write the slope-intercept form of the equation of the line through the given point and parallel to the given line?
Point (−2,−16), y = x – 5
You should answer part of this question in the group quiz. (L) Consider the function
f(x, y, z) = cos(πx)е³-²
(a) Evaluate the function at the point (1,1,1).
(b) Find the tangent plane to the function at this point.
(c) Use your tangent plane expression to give an approximation f(1.1, 1.1, 1.1).
Answers
Evaluating the function f(1, 1, 1) = -е³-², we find that it equals -е³-². The equation of the tangent plane to the function at (1, 1, 1) is -2z + 2 = 0 or z = 1. Using the equation of the tangent plane, the approximation of f(1.1, 1.1, 1.1) is 0.
(a) Evaluating the function f(x, y, z) = cos(πx)е³-² at the point (1, 1, 1), we substitute x = 1, y = 1, and z = 1 into the function:
f(1, 1, 1) = cos(π(1))е³-² = cos(π)e³-² = (-1)e³-² = -е³-².
(b) To compute the tangent plane to the function at the point (1, 1, 1), we need to compute the gradient of the function at that point. The gradient of f(x, y, z) is given by ∇f(x, y, z) = (-πsin(πx)е³-², 0, -2cos(πx)е³-²).
Evaluating the gradient at (1, 1, 1), we have ∇f(1, 1, 1) = (-πsin(π), 0, -2cos(π)) = (0, 0, -2).
The equation of the tangent plane is then given by:
0(x - 1) + 0(y - 1) + (-2)(z - 1) = 0,
which simplifies to -2z + 2 = 0 or z = 1.
(c) Using the tangent plane expression obtained in part (b), we can approximate f(1.1, 1.1, 1.1) by substituting x = 1.1, y = 1.1, and z = 1.1 into the equation of the tangent plane:
0(1.1 - 1) + 0(1.1 - 1) + (-2)(1.1 - 1) = 0.
Simplifying, we find that the approximation is 0.
Therefore, the approximation of f(1.1, 1.1, 1.1) using the tangent plane at the point (1, 1, 1) is 0.
To know more about tangent plane refer here:
https://brainly.com/question/30565764#
#SPJ11
is this right pls...

Answers
Answer:
yes
Step-by-step explanation:
What are the domain and range of the function f(x)= x+5?

Answers
Answer:
top answer, domain and range have no restrictions
Step-by-step explanation:
Select each relation that has a range of {-5, 0, 4, 7}?
Responses
A{(4, 2), (0, 6), (-5, 12), (7, 6), (4, -3)}
B{(18, 4), (-1, 0), (-3, -5), (6, 7), (2, 4)}
C{(6, -5), (-11, 0), (6, 4), (-3, 7), (2, 9)}
D{(0, 6), (-5, 12), (7, 6), (4, -3)}
E{(6, -5), (-2, 4), (4, 7), (1, 0)}
F{(-5, 4), (-2, 4), (4, 7), (1, 0)}
Answers
Answer: E and B
I did the quiz
A relation that has a range of {-5, 0, 4, 7} is:{(6, -5), (-2, 4), (4, 7), (1, 0)}
The correct answer is an option (E)
In this question, we have been given some relations.
We need to find a relation that has a range of {-5, 0, 4, 7}
We know that in a relation is a set of ordered pairs (x, y)
where x is input and y is output.
We know that range is collection of all output values.
Therefore, a relation that has a range of {-5, 0, 4, 7} is:
E {(6, -5), (-2, 4), (4, 7), (1, 0)}
Learn more about a relation here:
https://brainly.com/question/13088885
#SPJ1
Let f(x)=x-6 and g(x) = 4x². Perform the function operation and then find the domain of the result.
(f+g)(x)
Answers
Answer:
4x^2 + x - 6.
Step-by-step explanation:
(f + g)(x)
= f(x) + g(x)
= x - 6 + 4x^2
= 4x^2 + x - 6.
Find the inverse please tell me where to put the dots thanks
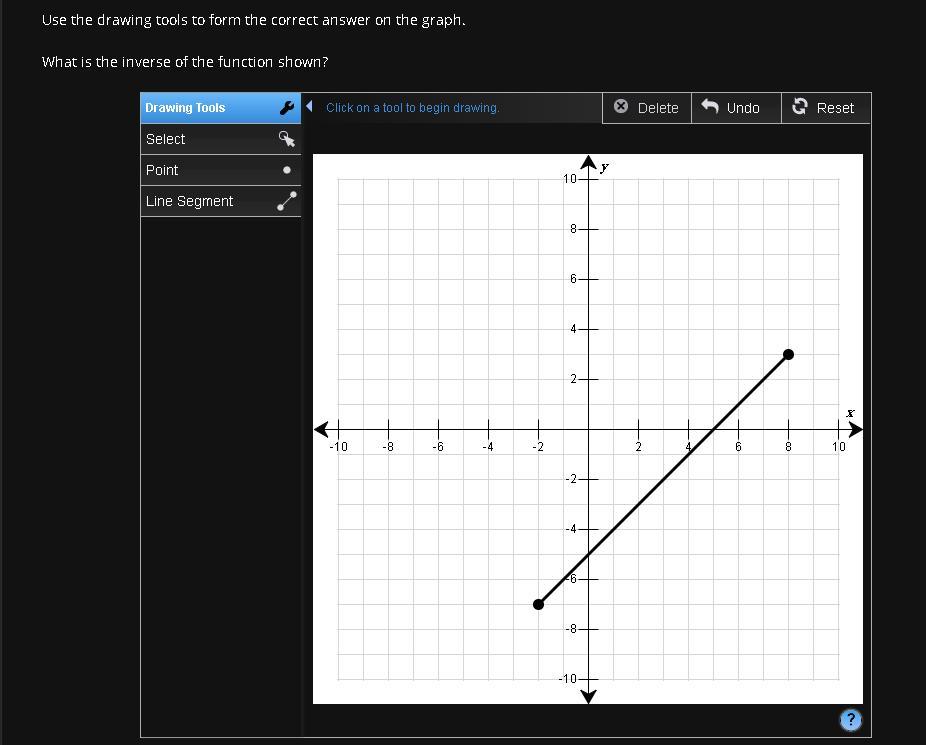
Answers
Answer:
Draw a line segment from (-7, -2) to (3, 8)
See the diagram below.
You do not have to draw the blue dashed line. It's there to show how the points reflect over.
=========================================================
Explanation:
The inverse will have us swap x and y. The point (x,y) becomes (y,x)
The endpoint (-2, -7) becomes (-7, -2)
Also (8,3) moves to (3, 8)
Visually, these points are being reflected over the line y = x to form the inverse. We only need to worry about the endpoints because 2 points is the minimum needed to form a straight line.
Check out the diagram below. The red segment is the inverse. The blue dashed line is the line y = x. You don't have to plot this line as it's just a visual tool to see what's going on. Your teacher likely will only want the red segment.
Since the original segment is parallel to y = x, the inverse is also parallel to the mirror line. All three lines are parallel.

A line passes through the point (6,-8) and has a slope of -3. Write an equation in slope-intercept form for this line.
Answers
Answer:
y = -3x + 10
Step-by-step explanation:
Equation of line in slope y-intercept form: y =mx + bHere m is the slope and b is the y-intercept.
m = -3
y = -3x + b
Now (6,-8) is passing through this line. So, substitute the x and y coordinates in the above equation and find the value of 'b'.
-8 = -3*6 + b
-8 = -18 + b
-8 +18 = b
b = 10
Equation of the line:
y = -3x + 10
Answer:
y=-3x+10
Step-by-step explanation:
slope intercept form is y=mx+b
m is slope
b is y intercept
So we fill in what we know to find b
-8=-3(6)+b
-8=-18+b
+18 +18
10=b
Now we can finish our equation
y=-3x+10
Hopes this helps please mark brainliest
Find the slope of the line that passes through the points A(-3, 1) and B(2, -5).
Answers
Answer:
\(m = \frac{ - 5 - 1}{2 - ( - 3)} = - \frac{6}{5} \)
How can you determine the sale price if you are given the regular price and the percent of markdown? (List the steps)
Answers
Answer:
The sale price is $34
Step-by-step explanation:
If we are given the regular price P and the markdown percentage r, we follow these steps:
1) Calculate the markdown or discount amount M.
M = P*r/100
2) Subtract it from the regular price:
S = P - M
S is the sale price.
Example: The regular price is $40 and the markdown percentage is 15%. Thus:
1) M = $40*15/100 = $6
2) S = $40 - $6 = $34
The sale price is $34
Need help asap with this I would appreciate the help:0

Answers
Step-by-step explanation:
tan K = 32/24 = 4/3
hope this helps you.
Answer:
tan K = 4/3
Step-by-step explanation:
Tangent puts together the OPPOSITE side of a triangle compared to the ADJACENT side in a ratio (looks like a fraction)
tan K = 32/24 reduce this fraction for your final answer.
tan K = 4/3
Can someone please help me

Answers
Answer:
\(y = + - \sqrt[4]{ \frac{3}{2} x} \)
Last week, Clay had a beginning balance of $50 in his account. He wrote 2 checks for $23 each from his checking account , withdrew another $5, and finally made a deposit of $22. Part A: Write an expression and your answer to show his final account balance at the end of the week 23 * 2 = 46 Part B: Explain in words, what Clay should do to get his accaunt balance to zero?
Answers
Answer:
Part A
y =($50 - ($23 × 2 + $5)+ $22)
y = $21
Part B
Clay can get his balance to zero by withdrawing or writing another check for $21
Step-by-step explanation:
Last week, Clay had a beginning balance of $50 in his account. He wrote 2 checks for $23 each from his checking account , withdrew another $5, and finally made a deposit of $22.
Part A: Write an expression and your answer to show his final account balance at the end of the week 23 * 2 = 46
Let his final Account Balance = y
y =($50 - ($23 × 2 + $5)+ $22)
y =$72 - $51
y = $21
Part B: Explain in words, what Clay should do to get his account balance to zero?
Clay can get his balance to zero by withdrawing or writing another check for $21
= $21 - $21
= $0
what percentage of 36 is 18
Answers
Answer:
18/36×100%
The answer will be 50
Step-by-step explanation:
Hope it helps you
can some one do this for me i will give you Brainliest

Answers
Answer:
1. 1
2. -30
3. -2
4. 15
Step-by-step explanation:
A manufacturing machine has a 1% defect rate. If 3 items are
chosen at random, what is the probability that at least one will
have a defect? (round to 4 decimal places)
Answers
The defect rate is given as 1%, which means the probability of an item not having a defect is 99%. By applying this probability to each of the three items and subtracting from 1, we can determine the probability of at least one defect.
The probability of an item not having a defect is 99% or 0.99. Since the items are chosen independently, the probability of all three items not having a defect is obtained by multiplying the probabilities for each item: 0.99 * 0.99 * 0.99 = 0.970299.
This represents the complementary probability of none of the items having a defect. To find the probability of at least one defect, we subtract this value from 1: 1 - 0.970299 = 0.0297. Therefore, the probability that at least one item will have a defect is approximately 0.0297 or 2.97% when rounded to four decimal places.
Visit here to learn more about probability:
brainly.com/question/13604758
#SPJ11
in a box of chocolates, 1/5 of the chocolates contain nuts. the rest of the chocolates do not contain nuts. write down the ratio of the number of chocolates that contain nuts to the number of chocolates that do not contain nuts. give your answer in the form 1:n
Answers
Answer:
The ratio of the number of chocolates that contain nuts to the number of chocolates = 1:4
Step-by-step explanation:
The parameters given are;
Proportion of the box of chocolates that contain nuts = 1/5
Proportion of the box of chocolates that do not contain nuts = 1 - 1/5 = 4/5
Therefore, we have in a box of chocolates with five chocolates;
The number of chocolates that contain nuts = 1
The number of chocolates that do not contain nuts = 4
Which gives the ratio of the number of chocolates that contain nuts to the number of chocolates as 1:4.
For a ride on the rental scooter, Omar paid an $8 fee to start the scooter plus 6 cents per minute of the ride. The total bill for Omar’s ride was $19.34 for how many minutes did Omar ride the scooter?
Answers
Explanation
Given that Omar paid an $8 fee to start the scooter plus 6 cents per minute of the ride. We can express this as
Let the number of minutes be x. Therefore, we will have
\(\frac{6}{100}x=0.06x\)as the payment for riding the bicycle over x minutes.
Therefore, since the total bill for Omar’s ride was $19.34, we will have;
\(0.06x+8=19.34\)Hence;
\(\begin{gathered} 0.06x+8=19.34 \\ 0.06x=19.34-8 \\ 0.06x=11.34 \\ x=\frac{11.34}{0.06} \\ x=189 \end{gathered}\)Answer: 189 minutes
solve for x
4x^2+4=-17x
if there is more than one solution, separate them with commas. if there is no solution, click "no solution"
Answers
The equation is :
4x^2+ 17x+ 4
factorise it by:
= 4x^2 +x - 16x +4
= x(4x+1)-4( 4x-1)
=(x-4) (4x+1) (4x-1)
Hence x =4, -1/4,1/4 .
Hope this helps you.
All the outcomes contained in one or the other of two random events, or possibly in both, make up:
Question options:
the intersection of two events
the union of two events
the probability space of an experiment
the events of an experiment
Answers
The outcomes contained in one or the other of two random events, or possibly in both, make up the union of two events.
In probability theory, the union of two events refers to the set of outcomes that are present in either one or both of the events. It represents the combination of all possible outcomes from the individual events.
For example, let's consider two events A and B. The union of these events, denoted as A ∪ B, includes all the outcomes that belong to event A, event B, or both. It represents the combined set of outcomes from the two events.
Mathematically, the union of two events is defined as:
A ∪ B = {x | x ∈ A or x ∈ B}
So, when we talk about the outcomes contained in one or the other of two random events, or possibly in both, we are referring to the union of those events. The union captures all the possible outcomes that can occur in either event or in both events simultaneously.
To learn more about probability click here
brainly.com/question/31828911
#SPJ11
what is pythagorean theorm?
Answers
Answer:
In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
Step-by-step explanation:
Answer:
In mathematics, the Pythagorean theorem, also known as Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b, and c, often called the "Pythagorean equation"
Step-by-step explanation:
Answer number eleven and thirteen please

Answers
Answer:
Both are right trianglesStep-by-step explanation:
Use Pythagorean to decide
#11Sides 12, 16, 20
12² + 16² = 20²400 = 400Right triangle#13Sides 2.4, 4.5, 5.1
2.4² + 4.5² = 5.1²26.01 = 26.01Right triangle\(g(x) = x - 3\)\(f(x) = 2x^{3} \)Find f(x)Find g(4)Find (f+g)(x)Find f(0)+g(2)Find f(3)+g(0)Find f(-1) -f(1)+g(2)
Answers
g(x) = x - 3
f(x) = 2x³
to find g(4), replace x = 4 in g(x) formula, as follows:
g(4) = 4 - 3 = 1
(f+g)(x) = f(x) + g(x) = 2x³ + x - 3
f(0)+g(2) = 2(0)³ + (2) - 3 = 2 - 3 = -1
f(3)+g(0) = 2(3)³ + (0) - 2 = 2(27) - 2 = 54 - 2 = 52
f(-1) -f(1)+g(2) = 2(-1)³ - 2(1)³ + 2 - 3 = 2(-1) - 2(1) + 2 - 3 = -2 - 2 + 2 - 3 = -5
What is the absolute value of -11

Answers
Answer:
11
Step-by-step explanation:
11
since it asks the absolute value of -11 it
will be 11 because in absolute value-for negatives it always positive.
Answer:
see attached
Step-by-step explanation:

The
square
root of
80
Answers
= 4 x sqrt(5)

What is the probability that a randomly selected airfare between these two cities will be more than $450?
Answers
The probability that a randomly selected airfare between these two cities will be more than $450 is 0.2033.
Given:
Mean (μ) = $387.20
Standard deviation (σ) = $68.50
To find the probability that a randomly selected airfare between Philadelphia and Los Angeles will be more than $450,
calculate the area under the normal distribution curve above the value of $450.
Step 1: Standardize the value of $450.
To standardize the value, we calculate the z-score using the formula:
z = (X - μ) / σ
z = ($450 - $387.20) / $68.50
z= 0.916
So, the area to the right of the z-score approximately equals 0.2033.
Therefore, the probability that a randomly selected airfare between these two cities will be more than $450 is 0.2033.
Learn more about Probability here:
https://brainly.com/question/28146696
#SPJ4
The question attached here seems to be incomplete, the complete question is:
Suppose the round-trip airfare between Philadelphia and Los Angeles a month before the departure date follows the normal probability distribution with a mean of $387.20 and a standard deviation of $68.50. What is the probability that a randomly selected airfare between these two cities will be more than $450?
0.0788
0.1796
0.2033
0.3669
A friend who works in a big city owns two cars, one small and one large. Three-quarters of the time he drives the small car to work, and one-quarter of the time he drives the large car. If he takes the small car, he usually has little trouble parking, and so is at work on time with probability 0.9. If he takes the large car, he is at work on time with probability 0.6. Given that he was on time on a particular morning, what is the probability that he drove the small car?A. 0.890.B. 0.768.C. 0.829.D. None of the listed.
Answers
the probability that he drove the small car is 0.890 (option A).
Using Bayes' theorem to solve the problem given, let us represent the following events:
A: Friend drives the small carB: Friend drives the large carC: Friend is on timeGiven that three-quarters of the time he drives the small car and one-quarter of the time he drives the large car, we can calculate the prior probabilities:
P(A) = 3/4 and P(B) = 1/4.
Also, given that he usually has little trouble parking with probability 0.9 when driving the small car and is on time with probability 0.6 when driving the large car, we can calculate the likelihoods:
P(C|A) = 0.9 and P(C|B) = 0.6
Using Bayes' theorem, we can calculate the posterior probability of driving the small car given that he was on time on a particular morning:
P(A|C) = P(C|A) * P(A) / (P(C|A) * P(A) + P(C|B) * P(B))= 0.9 * 3/4 / (0.9 * 3/4 + 0.6 * 1/4) = 0.890
for more questions on probability
https://brainly.com/question/13076729
#SPJ11
If fuses cost $2.35 each, and each motor requires 3 fuses, how many motors can be supplied with $493.50 worth of fuses?
Answers
From the statement we know that:
• fuses cost $2.35,
,• a motor requires 3 fuses, so it requires Cm = 3 * $2.35 = $7.05 of cash for the fuses,
,• we have $493.5 of cash to invest.
So the amount of motors that we can supply is:
\(\frac{493.5}{C_m}=\frac{493.5}{7.05}=70\)Answer
We can supply 70 motors.
What is the prime factorization of 32?
A. 2 × 32
B 23
C 24
D 25?
Answers
2 × 32 is the prime factorization of 32 .
What does prime factorization refer to?
Writing all numbers as the product of primes is a procedure known as prime factorization. Hence, let's use the example of the number 20, for example. It can be divided into two components. We can respond, "Well, that's 4 times 5." You'll also see that 5 is a prime number.
Not being a prime number, 4 is. Any number can be expressed as the sum of its prime factors by being considered a prime factor. A number with exactly two elements, 1 and the number itself, is referred to as a prime number. For instance, the prime factorization of 18 is 2 3 3 (see illustration). Here, the two main elements of 18 are 2 and 3.
The prime factorisation of 32 is 2 x 2 x 2 x 2 x 2.
Learn more about prime factorization
brainly.com/question/29775157
#SPJ1