Raju is painting the walls and ceiling of a room with length, breadth and height of the room are 10m, 5m, 2m respectively. From each can of paint, 10m2 of area is painted. How many cans of paint will he need to paint the room?
Answers
Answer:
10 cans of paint
Step-by-step explanation:
Find the total area of the room
Divide the answer by 10meter squared.

Related Questions
Given that the line 3y - mx + 3 = 0 is parallel to the line y = x + 5, find the value of m..
Answers
Answer:
m= 3
Step-by-step explanation:
In the slope-intercept form (y= mx +c), the coefficient of x (when the coefficient of y is 1) is the slope.
y= x +5
Slope of line= 1
Parallel lines have the same slope, hence the slope of 3y -mx +3= 0 is also equal to 1.
Let's rewrite the equation into slope-intercept form.
Keep the y term on the left-hand side, bring the others to the right.
3y= mx -3
Divide both sides by 3:
\(y = \frac{m}{3} x - 1\)
Given that the slope is 1,
\( \frac{m}{3} = 1\)
Multiply both sides by 3:
m= 1(3)
m= 3
To learn more about equation of parallel lines, check out: https://brainly.com/question/21782167
An airliner carries 50 passengers and has doors with a height of 70 in. Heights of men are normally distributed with a mean of 69. 0 in and a standard deviation of 2. 8 in. Complete parts (a) through (d). A. If a male passenger is randomly selected, find the probability that he can fit through the doorway without bending. The probability is 0. 6406. (Round to four decimal places as needed. ) b. If half of the 50 passengers are men, find the probability that the mean height of the 25 men is less than 70 in. The probability is 0. 9633. (Round to four decimal places as needed. )
Answers
The probability is 0.6480.
The probability is 0.9629.
How to solve for the probability1. This can be computed using the standard normal distribution as follows:
z = (70 - 69.0) / 2.8 = 0.357
Using a standard normal table or calculator, we find that P(Z ≤ 0.357) ≈ 0.6480. Therefore, the probability that a male passenger can fit through the doorway without bending is approximately 0.6480.
2. = 2.8/√25 = 0.56 inches.
We want to find P(x < 70), which is the probability that the mean height of the 25 men is less than 70 inches. This can be standardized using the standard normal distribution as follows:
z = (70 - 69.0) / 0.56 = 1.79
Using a standard normal table or calculator, we find that P(Z < 1.79) ≈ 0.9629. Therefore, the probability that the mean height of the 25 men is less than 70 inches is approximately 0.9629.
Read more on probability here:https://brainly.com/question/24756209
#SPJ4
2(n-4) = 16 solve for n
Answers
Answer:
answer is 12
Step-by-step explanation:
2n-8=16
2n=24
n=12
Answer:
x=12
Step-by-step explanation:
divide both sides by 2
16/2=8
x-4=8
x=12
What is -15=-4m+5 equal and its two steps problems in HS
Answers
4m=20 /4
M= 5
the times that customers spend in a book store are normally distributed with a mean of 39.5 minutes and a standard deviation of 15.9 minutes. a random sample of 30 customers has a mean of 36.1 minutes. would this outcome be considered unusual, so that the store should reconsider its displays?
Answers
It would be considered unusual for a random sample of 30 customers to have a mean of 36.1 minutes.
To determine if this outcome is unusual, we can use a z-score, which compares the sample mean to the population mean using the standard deviation. The z-score for a sample mean of 36.1 minutes would be -1.87, which is considered to be in the lower tail of the normal distribution.
This means that the probability of getting a sample mean of 36.1 minutes or lower is less than 0.05. Therefore, this outcome is considered to be unusual, and the store should reconsider its displays.
For more questions like Probability click the link below:
https://brainly.com/question/30034780
#SPJ4
a 40 g particle is moving to the left at 25 m/s . how much net work must be done on the particle to cause it to move to the right at 51 m/s ? express your answer to two significant figures and include the appropriate units.
Answers
To cause the particle to move to the right at 51 m/s, the net work done on it must be equal to the change in kinetic energy. The initial kinetic energy of the particle is (1/2)mv^2 = (1/2)(40 g)(25 m/s)^2 = 31,250 J. The final kinetic energy of the particle is (1/2)mv^2 = (1/2)(40 g)(51 m/s)^2 = 52,020 J. Therefore, the net work done on the particle is 52,020 J - 31,250 J = 20,770 J.
To solve this problem, we'll use the work-energy theorem, which states that the net work done on an object is equal to its change in kinetic energy:
W = ΔKE = KE_final - KE_initial
First, we need to calculate the initial and final kinetic energies (KE) of the particle:
KE_initial = (1/2) * m * v_initial^2
KE_final = (1/2) * m * v_final^2
Given that the particle has a mass (m) of 40 g (0.04 kg) and initial velocity (v_initial) of -25 m/s (negative because it's moving to the left), we can find KE_initial:
KE_initial = (1/2) * 0.04 kg * (-25 m/s)^2 = 12.5 J
Similarly, with a final velocity (v_final) of 51 m/s (positive because it's moving to the right):
KE_final = (1/2) * 0.04 kg * (51 m/s)^2 = 52.404 J
Now, calculate the net work (W):
W = ΔKE = KE_final - KE_initial = 52.404 J - 12.5 J = 39.904 J
Expressed to two significant figures, the net work done on the particle is:
W ≈ 40 J
Learn more about Equal:
brainly.com/question/29194324
#SPJ11
Simplify. Assume that no denominator is equal to zero. (show work)
help please!!!!!

Answers
n^8
basically it's like this n^12/n^4 = n^(12-4) = n^8
Y is 5 less than the product of 4 and x
Answers
Answer: y=4x-5
Y=4x-5
Kathleen went to a natural science museum and bought an admission ticket that cost $21. She figured she could spend up to $19 on special exhibits to avoid spending too much in all. Let x represent how much money Kathleen wanted to spend in all. Which inequality describes the problem? Solve the inequality. Then, complete the sentence to describe the solution. Kathleen wants to spend at most $ in all.
Answers
The money Kathleen wanted to spend in all is x≤40.
Given that, Kathleen went to a natural science museum and bought an admission ticket that cost $21.
What are inequalities?Inequalities are the mathematical expressions in which both sides are not equal. In inequality, unlike in equations, we compare two values. The equal sign in between is replaced by less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.
Let x represent how much money Kathleen wanted to spend in all.
Here, Kathleen figured she could spend up to $19 on special exhibits to avoid spending too much in all.
So, the inequality will be x−21≤19
Add 21 on both the sides of a inequality, we get
x≤40
Hence, the money Kathleen wanted to spend in all is x≤40.
To learn more about the inequalities visit:
https://brainly.com/question/20383699.
#SPJ1
Nancy has x books.
Braveen has triple the number of books Nancy has, plus 5 more books.
Cal has double the number of books Braveen has.
In total, they have 245 books.
Which equation represents the total number of books for all three people?
Answers
The equation that represents the total number of books for all three people is 10x + 15 = 245. Nancy has 23 books.
What is an equation?
The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions.
Given that Nancy has x books.
Braveen has triple the number of books Nancy has, plus 5 more books.
Replace the number of books Nancy with x:
Braveen has 3x plus 5 more books.
Rewrite the above statement:
Braveen has 3x + 5 books.
Cal has double the number of books Braveen has.
Replace the number of books Braveen has with 3x+5:
Cal has double of 3x+5.
Cal has 2(3x+5)
The number of books they have is x + 3x + 5 + 2(3x+5)
Again given that they have 245 books.
According to the question,
x + 3x + 5 + 2(3x+5) = 245
x + 3x + 5 + 6x + 10 = 245
Combine like terms:
(x + 3x + 6x) +5 + 10 = 245
10x + 15 = 245
To learn more about the model equation, click on the below link:
https://brainly.com/question/20638226
#SPJ1
Can anyone help me with this question ?
I’ll mark you as a brainliest.
Please don’t answer if you do not know.

Answers
please help i don’t get it :(

Answers
10 x 10 = 100
the area is 100 m^2
Which of the following describes the graph shown?
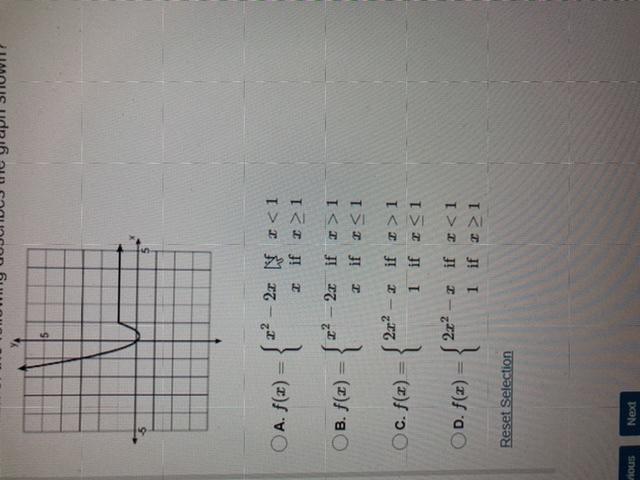
Answers
Answer:
it's option d you were right
How many 2 1/7 inch pieces of thread can be
cut from a spool with 8 3/4 inches of thread?
Answers
A spool of thread measuring 8 3/4 inches long and 4 inches wide can be cut into 2 1/7 inch pieces.
How many pieces of thread can be cut ?In light of the conditions stated, come up with: \($\frac{8 \frac{3}{4}}{2 \frac{1}{7}}$\) To improper fractions, change the mixed numbers to: \($\frac{\frac{35}{4}}{\frac{15}{7}}$\) Multiply the reciprocal of a fraction to get its division: \($\frac{35}{4} \times \frac{7}{15}$\)
Mark this common element as a no-go: Multiplying \($\frac{7}{4} \times \frac{7}{3}$\) Mark the common element as absent: Multiplying \($\frac{7 \times 7}{4 \times 3}$\) . Put the following in one fraction : \($\frac{49}{12}$\) . The product or quotient should be
calculated.Find the biggest number that is greater than \($\frac{49}{12}$\) and less than or equal to it . A spool of thread measuring 8 3/4 inches long and 4 inches wide can be cut into 2 1/7 inch pieces.Otherwise, you or a device will need to count 127 turns (the irreducible repeat, independent of thread pitch), after which the half nut must be closed.
To learn more about thread refer to :
https://brainly.com/question/2733060
#SPJ1
a regression model involved 5 independent variables and 136 observations. the critical value of t for testing the significance of each of the independent variable's coefficients will have group of answer choices 121 degrees of freedom. 135 degrees of freedom. 130 degrees of freedom. 4 degrees of freedom.
Answers
The critical value of t for testing the significance of each of the independent variable's coefficients will have 130 degrees of freedom.
This is because the degrees of freedom for a t-test in a regression model with 5 independent variables and 136 observations is calculated as (n - k - 1) where n is the number of observations and k is the number of independent variables.
Therefore, (136 - 5 - 1) = 130 degrees of freedom.
Visit here to learn more about variable's coefficients brainly.com/question/30024970
#SPJ11
Suppose you are holding stock and there are three possible outcomes. The good state happens with 20% probability and 18% return. The neutral state happens with 55% probability and 9% return. The bad state happens with 25% probability and −5% return. What is the expected return? Please enter the answer as a percent with two decimal places for instance 55.55 for 55.55% Suppose you are holding a stock and there are three possible outcomes. The good state happens with 20% probability and 18% return. The neutral state happens with 55% probability and 9% return. The bad state happens with 25% probability and −5% return. What is the standard deviation of return? Please enter a number (not a percentage). Please convert all percentages to numbers before calculating, then type in the number. Now type in 4 decimal places. The answer will be small. Suppose you are holding a stock and there are three possible outcomes. The good state happens with 20% probability and 18% return. The neutral state happens with 55% probability and 9% return. The bad state happens with 25% probability and −5% return. What is the variance of return? Please enter a number (not a percentage). Please convert all percentages to numbers before calculating, then type in the number. Now type in 4 decimal places. The answer will be small.
Answers
The standard deviation of returns is 0.0665 when a person is holding stock and there are three possible outcomes.
To calculate the expected return, we multiply the probability of each state by its corresponding return and sum them up:
Expected return = (20% * 18%) + (55% * 9%) + (25% * -5%)
Expected return = 0.20 * 0.18 + 0.55 * 0.09 + 0.25 * (-0.05)
Expected return = 0.036 + 0.0495 - 0.0125
Expected return = 0.073
The expected return is 7.30%.
To calculate the standard deviation of returns, we need to find the variance first. The variance is calculated as the weighted sum of squared deviations from the expected return:
Variance = (20% * (18% - 7.30%)^2) + (55% * (9% - 7.30%)^2) + (25% * (-5% - 7.30%)^2)
Variance = 0.20 * (0.1077)^2 + 0.55 * (0.0177)^2 + 0.25 * (-0.123)^2
Variance = 0.00232 + 0.000173 + 0.001903
Variance = 0.004423
The standard deviation is the square root of the variance:
Standard deviation = √(0.004423)
Standard deviation = 0.0665
Therefore, the value obtained is 0.0665.
To know more about standard deviation refer here:
https://brainly.com/question/29115611#
#SPJ11
Find a vector equation and parametric equations for the line. (Use the parameter t.) The line through the point (0, 15, −6) and parallel to the line x = −1 + 2t, y = 6 − 3t, z = 3 + 7t
Answers
<x = 0 + 2t, y = 15 - 3t, z = -6 + 7t> is the vector parametric equation of the line parallel to the given one and that passes through the point (0, 15, −6).
According to the statement
we have to find that the vector equation with the help of the given line equation and the points.
So, For this purpose, we know that the
A vector equation is an equation involving a linear combination of vectors with possibly unknown coefficients.
And the given points is (0, 15, −6) and the lines
x = −1 + 2t,
y = 6 − 3t,
z = 3 + 7t
From these equation of lines:
Let a = -1 and b = 6 and c = 3
Then
Now, if we want this line to pass through the point (0, 15, -6), then we can replace the correspondent values in the constant term for each equation:
So, Put it in the given equations then
x = 0 + 2t and y = 15 - 3t and z = -6 + 7t
and the vector equation become
<x = 0 + 2t, y = 15 - 3t, z = -6 + 7t>
So, <x = 0 + 2t, y = 15 - 3t, z = -6 + 7t> is the vector parametric equation of the line parallel to the given one and that passes through the point (0, 15, −6).
Learn more about vector parametric equation here
https://brainly.com/question/17088529
#SPJ4
two balls are drawn simultaneously from a bag containing 2 yellow and 4 green balls. what is the probability of drawing 2 green balls
Answers
The probability of drawing 2 green balls simultaneously from a bag containing 2 yellow and 4 green balls can be determined using the following method:
First, calculate the total number of balls in the bag. There are 2 yellow balls and 4 green balls, so the total is 6 balls.
Now, let's find the probability of drawing 2 green balls. To do this, consider the number of green balls (4) and the total number of balls (6). When drawing the first green ball, there are 4 green balls out of 6 total balls. Therefore, the probability of drawing one green ball is 4/6.
Since the balls are drawn simultaneously, there's no change in the number of balls for the second draw. So, the probability of drawing a second green ball remains 4/6.
Now, we can calculate the probability of both events occurring simultaneously by multiplying the probabilities:
(4/6) * (4/6) = 16/36
To simplify the fraction, divide both numerator and denominator by their greatest common divisor (4):
16/36 = 4/9
So, the probability of drawing 2 green balls simultaneously is 4/9.
To know more about Probability visit :
https://brainly.com/question/32004014
#SPJ11
What is actually true of all numbers and variables?
Answers
Answer: they are all ideas that are mutally agreed on.
Step-by-step explanation:
My math teacher told me this
Please help...a counselor wishes to examine the benefits of a parenting class on parenting
skills. he decides to administer a questionnaire to the 10 parents who have
attended the most recent class. how could this study be improved?
select all that apply.
a. administer a questionnaire to parents who have not attended the
class.
b. use a random sample of all patients, who have attended the
class.
c. increase the sample size.
d. give parents some sample responses, prior to administering the
questionnaire.
Answers
explanation
what is the point-slope form of a line with slope -4 that contains the point (-2, 3)
Answers
Answer:
\(y - 3 = - 4(x + 2)\)
given the slope of the line and one point that it passes through, represent the equation of the line in point-slope form. then rewrite the equation in slope-intercept form.
(-4,1);m=-2/3
Answers
Answer:
y=\(-\frac{2}{3}\)x\(-\frac{5}{3}\)
Step-by-step explanation:
y=mx+c
y= \(-\frac{2}{3}\)x+c
substitute (-4;1)
1=-\(-\frac{2}{3}\)(-4) +c
1-\(\frac{8}{3}\)=c
c=\(-\frac{5}{3}\)
Answer:
Step-by-step explanation:
answer on edmentum

Type the correct answer in the box.
A car accelerates from 4 meters/second to 16 meters/second in 4 seconds. The car's acceleration is
meters/second
Reset
Next
Answers
Answer:
3 meters/second
Step-by-step explanation:
acceleration = rate of change of speed (velocity)/change in time
= 16 - 4/4
= 12/4 = 3 m/s
please help me please will give brainliest to

Answers
Answer:
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. polynomials with real coefficients are included in this since every real number is a complex number with its imaginary part equal to zero.
Can I please get brainliest?
Answer:
It is non-constant variable polynomial with in depth coefficients and an in depth root.
Step-by-step explanation:
on: *2
2x - 8.
3x-2/4=2x-8
Answers
Answer:
x=-7.5
Step-by-step explanation:
3x-2/4=2x-8
-2x -2x
x-2/4=-8
+2/4 +2/4
Put separate terms on each side
x=-7.5
Please correct me if I'm wrong
Hope this helps!
How many hours is 7:45 to 1:00
Answers
Step-by-step explanation:
There are 17 hours between 7:45 to 1:00
6r - 6t = 6 and 3r - 6t = 15
Answers
Answer: r = -3, t = -4
Step-by-step explanation:
6r-6t=6
3r-6t=15
Using the elimination method, you can get
3r=-9
r=-3
Substitute -3 for r, and you get
-9-6t=15
-6t=24
t=-4
r=-3,t=-4
Answer:
r,t=-3,-4
Step-by-step explanation:
[1] 6r - 6t = 6
[2] 3r - 6t = 15
in a one-sample chi-square test, if your respondents are distributed very unequally across the levels of your variable, your chi-square value will be: a. high b. low c. 0 d. 1
Answers
The correct answer is a. high. In a one-sample chi-square test, the observed frequencies of the variable being studied are compared to the expected frequencies assuming a particular distribution or hypothesis.
The chi-square test statistic measures the difference between the observed and expected frequencies and determines whether this difference is statistically significant.
If the respondents are distributed very unequally across the levels of the variable being studied, the observed frequencies will be very different from the expected frequencies. This will result in a large difference between the observed and expected frequencies, leading to a high value for the chi-square test statistic.
The chi-square value is calculated by summing the squared differences between the observed and expected frequencies, divided by the expected frequencies. If the respondents are distributed very unequally across the levels of the variable being studied, the expected frequencies will be very different from the observed frequencies, resulting in a high value for the chi-square test statistic.
Therefore, in a one-sample chi-square test, if your respondents are distributed very unequally across the levels of your variable, your chi-square value will be high.
Learn more about chi-square here:
https://brainly.com/question/31871685
#SPJ11
The graph of g(x) is obtained by reflecting the graph of f(x) = 4 Ixl over the x-axis. = Which equation describes g(x)? O g(x) = -4 Ixl O g(x) = lx – 41 = O g(x) = lxl - 4 - g(x) = (x + 41 =

Answers
To answer this question, we need to remember that if we have the function f(x), the function -f(x) is the reflection of the function f(x) in the x-axis.
Then, the graph of the function g(x) is the same as g(x) = -f(x). Then, we have that:
\(g(x)=-f(x)\Rightarrow f(x)=4|x|\Rightarrow-f(x)=-4|x|\)Then
\(g(x)=-4|x|\)We can check this graphically as follows (the red graph is the function f(x) = 4|x| and the blue function is g(x) = -4|x|):
Therefore, g(x) = -4|x| is the reflection of the function f(x) = 4|x| over the x-axis.
In summary, the equation that describes g(x) is:
\(g(x)=-4|x|\)(First option).


consider all bit strings of length 12 How many have exactly four 1s? A. 4! B. C(12, 4) C. P(12, 4) D. 4*28 E. 28
Answers
The number of bit strings of length 12 that have exactly four 1s can be determined using the combination formula C(12, 4), which represents the number of ways to choose four elements out of twelve. Therefore, the answer is option b.
To find the number of bit strings with exactly four 1s, we need to select the positions for these four 1s from the total of twelve positions. The combination formula C(n, k) represents the number of ways to choose k elements from a set of n elements without regard to their order. In this case, we have twelve positions and need to choose four of them to place the 1s, so we can calculate C(12, 4).
Using the formula for combinations, C(n, k) = n! / (k! * (n-k)!), we can calculate C(12, 4) as follows:
C(12, 4) = 12! / (4! * (12-4)!) = 12! / (4! * 8!) = (12 * 11 * 10 * 9) / (4 * 3 * 2 * 1) = 495.
Therefore, there are 495 different bit strings of length 12 that have exactly four 1s, and the correct answer is option B, C(12, 4).
Learn more about ways here:
https://brainly.com/question/47446
#SPJ11