Si:
6+x=z
9+x=y
z+y=31
Cuanto equivale x y z
ayuda .90
Answers
Answer:
en comentario te envio el paso a paso. X=8 Z=14
Step-by-step explanation:
YA VOY
Related Questions
(1 point) find all values of k for which the function y=sin(kt) satisfies the differential equation y″ 20y=0. separate your answers by commas.
Answers
the only values of k for which y = sin(kt) satisfies the differential equation y″ - 20y = 0 are k = nπ/t for any integer n.
We are given the differential equation y″ - 20y = 0, and we need to find all values of k for which y = sin(kt) satisfies this equation.
First, we find the second derivative of y with respect to t:
y′ = k cos(kt)
y″ = -k^2 sin(kt)
Now we substitute these expressions for y, y′, and y″ into the differential equation:
y″ - 20y = (-k^2 sin(kt)) - 20(sin(kt)) = 0
Factorizing out sin(kt), we get:
sin(kt)(-k^2 - 20) = 0
This equation is satisfied when either sin(kt) = 0 or (-k^2 - 20) = 0.
When sin(kt) = 0, we have k = nπ/t for any integer n.
When (-k^2 - 20) = 0, we have k^2 = -20, which has no real solutions.
To learn more about derivative visit:
brainly.com/question/30365299
#SPJ11
I need this by tonight would be appreciated. :) I know this is basic stuff I'm in Middle School but when I signed up for this there wasn't a middle school option.

Answers
The area of the floor of the convenience store would be = 212.5 ft²
What is the area of an object?The area of an object is defined as the total space that is being occupied by that object.
To calculate the area of the convenience store is to find the area of the shaded part which would be = area of square - area of the triangle.
Area of square = l ×w = 15 × 15 = 225ft²
Area of triangle= 1/2 base ×height
= 1/2 × 5 × 5
(Note: 15 - 10 = 5 ft from the diagram used as base and height)
= 25/2
= 12.5 ft²
The area of the convenience store;
= 225 - 12.5
= 212.5 ft².
Therefore, the area that is covered by the convenience store should be = 212.5ft².
Learn more about area here:
https://brainly.com/question/28020161
#SPJ1
11. An amusement park charges $45 per person for admission. A season pass
costs $112 per person.
a. Write the first five terms of an arithmetic sequence that represents the
total cost of admission for the number of visits in a season.
b. How many times does a person have to visit the park for a season pass
to be the better deal? Explain.
Answers
Answer:
Step-by-step explanation:
The answer would be A. 1 1/5
48/40 = 1 8/40
1 8/40 Simplify to 1 1/5
Hope this helps!
1) How does the mean score from your first 30 rolls compare to the mean score of the sampling distribution? The mean of the first 30 rolls is(0.4) The mean of the sampling distribution is (1.03) 2)
How does the standard deviation from your first 30 rolls compare to the standard deviation of the sampling distribution? The standard deviation of the first 30 rolls is (0.96847) The standard deviation of the sampling distribution is (0.38358)
i am reposting it because the last answer didn't make any sense,please answer both questions properly and neatly as I have provided the data for both questions, thank you in advance, let me know if you want to see the entire question and previous questions
Answers
The mean score from the first 30 rolls is 0.4. The standard deviation of the first 30 rolls is 0.96847. The standard deviation of the sampling distribution is 0.38358.
The mean of the sampling distribution is 1.03. It is essential to note that the mean of the sampling distribution is the same as the expected value of the population.
A sampling distribution is a probability distribution of a statistic that is made up of all possible samples of a given size from a population of a certain size.
In this case, the population is all the scores one could get when rolling a die.The sample mean is compared to the population mean using a t-test or a z-test.
These tests enable statisticians to determine whether the mean of a sample is significantly different from the population mean. If the p-value is smaller than the significance level, the null hypothesis can be rejected.
The null hypothesis is that the sample is not significantly different from the population.The standard deviation of the first 30 rolls is 0.96847. The standard deviation of the sampling distribution is 0.38358.
The standard deviation of the sampling distribution is much lower than that of the first 30 rolls. The sampling distribution has a smaller spread or variance, indicating that the sample mean is a more precise estimate of the population mean.
In other words, as the sample size grows, the standard deviation of the sampling distribution decreases. The standard deviation of the sampling distribution is inversely proportional to the square root of the sample size.
To know more about standard deviation refer here:
https://brainly.com/question/29758680#
#SPJ11
Age old help!!!!!!
…….

Answers
Answer:
Zoe was 32 years old, which was 4 years ago.
Step-by-step explanation:
When Zoe was 36 years old, her daughter was 1/3 her age, or 12 years old. Therefore, the difference in ages is 24 years.
So, our equation becomes:
4(Z-24) = Z
4Z - 96 = Z
3Z = 96
Z = 32
Assuming Zoe is 36 years old right now, our answer is 4 years ago.
Hope this helped,
~cloud
Since the daughter is 1/3 Zoe's age, she must be 12 since 1/3 of 36 is 12.
Then make a chart like I have done in the image attached.
Since the problem says "how many years ago", we use
our x years ago column in our chart to setup the equation.
If you need any additional help or are confused on a step, let me know!

Vance bought 2 packages of large beads and 1 package of medium beads. He bought 2 packages of large buttons and how many more beads than more buttons did vance buy
Answers
There are 472 more buttons bought by Vance than beads.
Define the term difference of number?One of the most crucial arithmetic operations, that is obtained by removing two integers, produces difference in mathematics.For the stated question table is made.
So,
Total number of beads bought by Vance = Number of beads(2 packages of large beads) + Number of beads(1 package of medium beads).
= (2 × 96) + (1 × 64)
= 2 × (90 + 6) + 64
= (2 × 90) + (2 × 6) + 64
= 180 + 12 + 64
= 256 beads
Now,
Total number of buttons bought by Vance = Total number of buttons (2 packages of large buttons) + Number of buttons (2 packages of medium buttons)
= (2 × 56) + (2 × 38)
= 2 × (50 + 6) + 2 × (30 + 8)
= (2 × 50) + (2 × 6) + (2 × 30) + (2 × 8)
= 100 + 12 + 600 + 16
= 728 buttons
Thus,
Difference for the number of buttons and beads
= 728 – 256
= 472 beads
So,
Therefore, there are 472 more buttons bought by Vance than beads.
Know more about the difference of number, here
https://brainly.com/question/18591813
#SPJ4

What the answer is? Please answer fast!

Answers
Answer:
A
Step-by-step explanation:
it includes all the combinations.
In your reservoir, you have a production well which flows for 48 hours at 200 STB/day, and then shut-in for 24 hours. The following additional data are given : Pi = 3100 psi Ct = 15x10^-6 psi^-1 Bo = 1.3 bbl/STB ϕ = 15% μ=1.2 cp K = 45 md and h = 60 ft
a-) Calculate the pressure in this production well at 12 hours of shut in
b-) Explain how can you use superposition in time to analyze a pressure build-up test.
Answers
a) To calculate the pressure at 12 hours of shut-in:
substitute the given values into the pressure buildup equation and solve for P(t=12).
b) Superposition in time is used in pressure buildup analysis by adding or summing the responses of multiple transient tests to analyze and interpret reservoir behavior and properties.
We have,
a) To calculate the pressure in the production well at 12 hours of a shut-in, we can use the equation for pressure transient analysis during shut-in periods, known as the pressure buildup equation:
P(t) = Pi + (Q / (4πKh)) * log((0.14ϕμCt(t + Δt)) / (Bo(ΔP + Δt)))
Where:
P(t) = Pressure at time t
Pi = Initial reservoir pressure
Q = Flow rate
K = Permeability
h = Reservoir thickness
ϕ = Porosity
μ = Viscosity
Ct = Total compressibility
t = Shut-in time (12 hours)
Δt = Time since the start of the flow period
Bo = Oil formation volume factor
ΔP = Pressure drop during the flow period
Given:
Pi = 3100 psi
Q = 200 STB/day
K = 45 md
h = 60 ft
ϕ = 15%
μ = 1.2 cp
Ct = 15x10^-6 psi^-1
Bo = 1.3 bbl/STB
t = 12 hours
Δt = 48 hours
ΔP = Pi - P(t=Δt) = Pi - (Q / (4πKh)) * log((0.14ϕμCt(Δt + Δt)) / (Bo(ΔP + Δt)))
Substituting the given values into the equation:
ΔP = 3100 - (200 / (4π * 45 * 60)) * log((0.14 * 0.15 * 1.2 * 15x\(10^{-6}\) * (48 + 48)) / (1.3 * (3100 - (200 / (4π * 45 * 60)) * log((0.14 * 0.15 * 1.2 * 15 x \(10^{-6}\) * (48 + 48)) / (1.3 * (0 + 48))))))
After evaluating the equation, we can find the pressure in the production well at 12 hours of shut-in.
b) Superposition in time is a principle used in pressure transient analysis to analyze and interpret pressure build-up tests.
It involves adding or superimposing the responses of multiple transient tests to simulate the pressure behavior of a reservoir.
The principle of superposition states that the response of a reservoir to a series of pressure changes is the sum of the individual responses to each change.
Superposition allows us to combine the information obtained from multiple tests and obtain a more comprehensive understanding of the reservoir's behavior and properties.
It is a powerful technique used in reservoir engineering to optimize production strategies and make informed decisions regarding reservoir management.
Thus,
a) To calculate the pressure at 12 hours of shut-in:
substitute the given values into the pressure buildup equation and solve for P(t=12).
b) Superposition in time is used in pressure buildup analysis by adding or summing the responses of multiple transient tests to analyze and interpret reservoir behavior and properties.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ12
3.2 less than a number t is at most 7.5.
Answers
Answer:
10.7
Step-by-step explanation:
10.7-3.2 is at most 7.5
In RISC-V, x0 always stores 0. a. x0 cannot be used to store a result so seems of limited use. Provide two uses of x0 to demonstrate its usefulness.
Answers
Two uses of x0 to demonstrate its usefulness are Function return value and Zero-extension.
x0 (also known as xzero) is a special-purpose register in the RISC-V architecture that always stores the value 0. Despite its seemingly limited use, x0 plays an important role in the RISC-V instruction set architecture. Here are two uses of x0:
Function return value: In RISC-V, the return value of a function is typically stored in the register x0. By convention, a function returns 0 if it executes successfully, and a non-zero value if it encounters an error. By using x0 to store the return value, the CPU can quickly determine the status of the function without having to access memory.
Zero-extension: When performing arithmetic operations, it is often necessary to extend the width of a register from a smaller size to a larger size. For example, when adding two 32-bit values, the result may require more than 32 bits to store. The RISC-V instruction set includes a zero-extension instruction that allows the contents of a register to be extended to a larger size, with the high-order bits being set to 0. x0 can be used as the destination register for this instruction, allowing the contents of another register to be extended to a larger size and stored in x0.
By serving as a quick reference to 0, x0 can help reduce the number of instructions needed to execute a program and improve performance.
Therefore, Two uses of x0 to demonstrate its usefulness are Function return value and Zero-extension.
To learn more about arithmetic operations,
Visit; brainly.com/question/29156854
#SPJ4
Which sets of three numbers represent the sides of an obtuse triangle?a. 4, 7, 8 b. 3, 4, 5 c. 2, 2, 3 d. 6, 8, 9 e. 3, 5, 6
Answers
A triangle with given sides (2, 2, 3), and (3, 5, 6) is an obtuse triangle and can be determined using the Pythagorean theorem.
Given :
The sides of the triangle are 6 cm, 10 cm and 12 cm.
To determine which three numbers represent the sides of an obtuse triangle, we can use the Pythagorean theorem. According to the Pythagorean theorem, the square of the third side equals the sum of the squares of the short sides of a right triangle. That is:
(H)² = (P)² + (B)²
Obtuse Triangle:
An obtuse triangle is a triangle with one interior angle greater than 90 degrees. In an obtuse triangle, if one angle is greater than 90°, the sum of the other two angles is less than 90°.
Obtuse triangle condition: (P)² + (B)² < (P)²
Applying the obtuse triangle condition in option a) ( 4,7,8) is more than 8² .This means 4²+ 7²= 65 < 64. So option A) represents not an obtuse triangle.
Apply obtuse triangle condition in option B) (3,4,5) :
3² + 4² = 25
This is the same. Therefore, option B) does not represent an obtuse triangle.
Option C) applies the obtuse triangle condition: (2,2,3)
therefore, 2² + 2² < 3²
This is less than 3². So option C) represents an obtuse triangle. Apply
Option D) obtuse triangle condition greater than
Option D) (6,8,9) represents: 6² + 8² > 9²
Therefore, option D) does not represent an obtuse triangle.
Applying the obtuse triangle condition in option E) (3,5,6)
Which represents: 3² + 5² < 6²
This is less than 6².
Therefore, option E) represents an obtuse triangle.
Learn more about Obtuse Triangle:
https://brainly.com/question/1581660
#SPJ4
The sales tax on a purchase of $56 is 7.5%. What is the total purchase price, including the sales tax?A.$4.20B.$5.60C.$60.20D.$63.50
Answers
Answer:
C.) 60.20
Step-by-step explanation:
multiply 56 by 7.5% toget the amount of sales tax which is 4.2 then add that to 56 to get the total amount.
Answer:
C. $60.2
Step-by-step explanation:
$56 + (0.075)(56) = 56 + 4.2
= $60.2
(q1) Find the length of the curve described by the function
, where

Answers
The length of the curve described by the function is approximately 21.14 units.
The length of the curve described by the function y = f (x) can be found using the formula below:$$\int_{a}^{b} \sqrt{1+\left[\frac{d y}{d x}\right]^{2}} d x$$
Where, a and b are the limits of the function.The function is y = 3x² + 4, which is a quadratic function.
Therefore, the derivative of y can be obtained as follows:$$\frac{d y}{d x} = 6x$$
Substitute the derivative of y into the formula to obtain:$$\int_{a}^{b} \sqrt{1+(6 x)^{2}} d x$$Integrating,
we have:$$\int_{a}^{b} \sqrt{1+36 x^{2}} d x$$Let u = 1 + 36x², then du/dx = 72x
which implies dx = 1/72 du/u^(1/2).
Hence, the integral is transformed to:
$$\frac{1}{72} \int_{1}^{37} u^{1 / 2} d u$$
Therefore, the integral is equal to:
$$\frac{1}{72}\left[\frac{2}{3} u^{3 / 2}\right]_{1}^{37}
= \frac{1}{72}\left[\frac{2}{3}\left(37^{3 / 2}-1\right)\right] \approx \boxed{21.14}$$T
To learn more about : length
https://brainly.com/question/28322552
#SPJ8
-1/3d + 4/5 = 1/2 what is d?
Answers
The required value of d in the given arithmetic operation is 9/10.
What are subtraction and addition?
The two main arithmetic operations that we learn to add and subtract two or more integers or other mathematical values are addition and subtraction. To add, one must add two or more numbers or values to produce a new number. The inverse of addition is subtraction and vice versa.
For instance, 10 - 1 = 9 if 9 + 1 = 10. That demonstrates that adding 1 produces the number 10 when added to 9, but subtracting 1 from 10 produces the number 9.
Given, -1/3d + 4/5 = 1/2
\(\frac{-1}{3} d+\frac{4}{5} =\frac{1}{2} \\\\\frac{-1}{3} d =\frac{1}{2}-\frac{4}{5}\\\\\frac{-1}{3} d = \frac{5-8}{10}\\\\\frac{-1}{3} d = \frac{-3}{10}\\\\\frac{d}{3}=\frac{3}{10}\\\\d = \frac{9}{10}\)
So, the required value of d = 9/10.
To learn more about subtraction and addition
https://brainly.com/question/20460320
#SPJ1
Y=-6x+2 -12-2y=-4 how many solutions does this linear equation have?
Answers
This linear equation system has a unique solution, which means it has only one solution.The given equations are:
Y = -6x + 2
-12 - 2y = -4
To find the number of solutions for this linear equation system, we can start by solving one equation for one variable and then substituting the solution into the other equation.
Let's solve the first equation, Y = -6x + 2, for Y:
Y = -6x + 2
Now let's solve the second equation, -12 - 2y = -4, for y:
-12 - 2y = -4
Adding 12 to both sides of the equation:
-2y = 8
Dividing both sides of the equation by -2:
y = -4
Now, we can substitute the value of y into the first equation:
Y = -6x + 2
Y = -6x + 2
Since Y is equal to -6x + 2 and y is equal to -4, we can set the two expressions equal to each other:
-6x + 2 = -4
Adding 4 to both sides of the equation:
-6x + 6 = 0
Subtracting 6 from both sides of the equation:
-6x = -6
Dividing both sides of the equation by -6:
x = 1
So, the solution to this linear equation system is x = 1 and y = -4.
Therefore, this linear equation system has a unique solution, which means it has only one solution.
To know more about linear equation visit:
https://brainly.com/question/29111179
#SPJ11
Evaluate the expression when x = 9.2 and y = 3.4.
5xy
Answers
5(9.2)(3.4)
156.4
Find the volume of the given prism.
Answers & photo below
↓
a. 64,288 ft3
b. 1,312 ft3
c. 2,009 ft3
d. 23,208 ft3

Answers
The volume of the cuboid is 64288 ft³
Volume of CuboidVolume of cuboid is the total space occupied by the cuboid in a three-dimensional space. A cuboid is a three-dimensional structure having six rectangular faces. These six faces of the cuboid exist as a pair of three parallel faces. Therefore, the volume is a measure based on the dimensions of these faces, i.e. length, width and height.
The formula of volume of a cuboid is given by
V = L * W * H
v = volume of cuboidl = length of cuboidw = width of cuboidh = height of cuboidSubstituting the values into the formula;
v = 41 * 32 * 49
v = 64288 ft³
The volume is 64288 ft³
Learn more on volume of a cuboid here;
https://brainly.com/question/22694657
#SPJ1
The option that indicates the correct volume of the rectangular prism in the photo that has the dimensions of length, 41 feet, width, 32 feet, and height, 49 feet is option a.
a. 64,288 ft³
What is a rectangular prism?A rectangular prism is a solid that has six rectangular faces, and twelve edges, in which each face has a parallel and congruent face on the opposite side of the prism, that has eight corners.
The dimensions of the rectangular prism in the question are;
Length of the rectangular prism = 41 feet
Width of the rectangular prism box = 32 feet
Height of the prism = 49 feet
The volume, V, of the rectangular prism is the product of the width, the length and the height as follows;
Volume of a rectangular prism, V = Width × Length × Height
The volume of the rectangular prism in the question is therefore;
V = 32 feet × 41 feet × 49 feet = 64,288 feet³
The volume of the rectangular prism in the question is; 64,288 ft³Learn more about rectangular prisms here:
https://brainly.com/question/3789826
#SPJ1
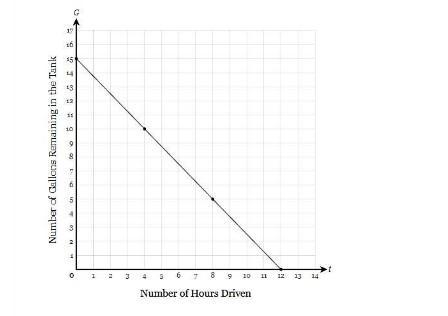
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
28-3(2+4)+9
With explanation
Answers
Answer:
Go through PEMDAS
Step-by-step explanation:
28-3(2+4)+92+4=628-3(6)+96+9=1528-3+1528-3=2525+15=40Answer:
19
Step-by-step explanation:
Result:
28 - 3(2 + 4) + 9 = 19/1 = 19
Spelled result in words is nineteen.
How do you solve fractions step by step?
Add: 2 + 4 = 6
Multiple: 3 * the result of step No. 1 = 3 * 6 = 18
Subtract: 28 - the result of step No. 2 = 28 - 18 = 10
Add: the result of step No. 3 + 9 = 10 + 9 = 19
HOPE THIS HELPS!
Find the average rate of change of the function \( f(x)=6 x \) from \( x_{1}=0 \) to \( x_{2}=7 \). The average rate of change is (Simplify your answer.)
Answers
The average rate of change is -6.
Given that, the function f(x)=6x from x₁=0 to x₂=7.
We know that for a given function f(x) the average rate of change on the interval a ≤ x ≤ b is given by: f(a)-f(b)/b-a
Here, f(x₁)=6x₁
f(0)=6×0=0
f(x₂)=6x₂
f(7)=6×7=42
So, (f(x₁)-f(x₂))/(x₂-x₁)
= (0-42)/(7-0)
= -42/7
= -6
Therefore, the average rate of change is -6.
Learn more about the average rate of change for function here:
https://brainly.com/question/23715190.
#SPJ4
I need help i'm never good at math :((

Answers
Answer:
The answer is d. (0,-6)
Step-by-step explanation:
If the distance from 0 to x on a number line is greater than 0, then -5 + x is positive?
True or false
Answers
So let's say that x is 2.
The statement is:
-2 + x is positive
-2 + 2 is positive
O is positive
This is not correct
Let's say that x is-2
-2 + x is positive
-2 + (-2) is positive
-2-2 is positive
-4 is positive
True.
Given the statement 'If the distance from 0 to x on a number line is greater than 5, then -5+x is positive' is True.
For the given question,
The distance from 0 to x on a number line is greater than 5
We write the above statement in mathematical expression form as,
⇒ |x - 0| > 5
⇒ |x| > 5
⇒ x > 5
We need to determine the value of an expression -5 + x
From (1),
⇒ x > 5
Subtract -5 from both sides,
⇒ -5 + x = -5 + 5
⇒ -5 + x > 0
From the above expression, we observe that the value of the expression is always greater than 1.
This means the value of an expression -5 + x is positive.
Therefore, the given statement 'If the distance from 0 to x on a number line is greater than 5, then -5+x is positive' is True.
In mathematics, a number line can be described as a figure that symbolizes numbers on a consecutive line. The digits on a number line are positioned successively with equal spacing along its length. It can be infinitely expanded in any direction and is often depicted horizontally.
Absolute value is the distance between a digit and zero on a number line. Since the space is forever positive, the absolute value will always be positive.
Learn more about the Number Line at
https://brainly.com/question/28345331?referrer=searchResults
Pls help taking finals
What is the value of w in the equation -W + 7 = 2w- 2?
Answers
Answer:
3
Step-by-Step explanation:
I just worked it out! Good luck :)
Estatura 5 ft 8 in peso 203 libras distancias corridas 597 yardas
Cuál es su estatura en metros
Cuántos metros ha corrido
En qué unidad que conozcas podrías expresar su peso Urge
Answers
The height in meters is 1.73 meters (rounded to two decimal places), the weight in other unit (kg) approximately 92.1 kg.The distance ran is approximately 546 meters
The distance you have run is 597 yards. To convert yards to meters, we can use the conversion factor 1 yard = 0.9144 meters. Therefore, the distance you have run in meters is approximately 546 meters (rounded to the nearest meter).
Your weight is currently expressed in pounds (lbs). To express your weight in other units, we can use conversion factors. For example, your weight in kilograms (kg) can be found by multiplying your weight in pounds by 0.453592. Using this conversion, your weight would be approximately 92.1 kg (rounded to one decimal place). Alternatively, your weight in stones (st) can be found by dividing your weight in pounds by 14. Using this conversion, your weight would be approximately 14.5 st (rounded to one decimal place).
Therefore, the hieght, weight and distance ran are 1.73 meters, 92.1 kg and 546 meters respectively.
Learn more about interconversion of units :
https://brainly.com/question/12791375
#SPJ4
The question is :
What is the height in meters and how many meters has he run, and in what unit could you express his weight, for someone who is 5 ft 8 in tall and weighs 203 lbs and ran a distance of 597 yards ?
if 8 people, consisting of 4 couoples, are randomly arranged in a row, find the probability that no person is next to their partner
Answers
According to the question The probability that no person is next to their partner is approximately 0.00022.
To find the probability that no person is next to their partner, we can consider the number of favorable outcomes and the total number of possible outcomes.
The total number of possible arrangements of 8 people is 8!, which is the factorial of 8 (8 factorial) and equals 40320.
Now, let's calculate the number of favorable outcomes, where no person is next to their partner. We can use the principle of derangements.
A derangement is a permutation of a set in which no element appears in its original position. In this case, we want to derange the 4 couples so that no person is next to their partner.
The number of derangements of 4 couples can be calculated using the formula for derangements:
\(D(4) = 4! * (1 - 1/1! + 1/2! - 1/3! + 1/4!)\)
= 9
So, there are 9 favorable outcomes where no person is next to their partner.
Therefore, the probability that no person is next to their partner is:
Probability = Number of favorable outcomes / Total number of possible outcomes
= 9 / 40320
≈ 0.0002232143
Rounded to 5 decimal places, the probability is approximately 0.00022.
To know more about probability visit-
brainly.com/question/32875821
#SPJ11
Christopher earns $5. 80 an hour and time-and-a-half for all hours over 40 hours. How much did he earn the week he worked 44. 5 hours?.
Answers
Answer: $271.15
Step-by-step explanation:
$5.80 × 40 = 232
Time and a half = $8.70
Overtime is 4.5 hours
$8.70 × 4.5 = 39.15
$232 + 39.15 = 271.15
67.5% of the 540 km road between the two cities is paved, while the rest is unpaved. the average speed of the car on paved roads was 25 km/h higher than on unpaved roads. find the speed of the car on a paved road if it took 10 hours to cover the entire road
Answers
Answer: Let's start by finding out the distance covered on paved and unpaved roads respectively.
Distance covered on paved road = 67.5% of 540 km = 0.675 x 540 = 364.5 km
Distance covered on unpaved road = 32.5% of 540 km = 0.325 x 540 = 175.5 km
Let the speed of the car on unpaved roads be x km/h. Then, the speed of the car on paved roads will be (x + 25) km/h.
Now, let's use the formula:
time = distance / speed
We know that the total time taken to cover the entire road is 10 hours.
So,
time taken on paved road + time taken on unpaved road = 10
or,
364.5 / (x + 25) + 175.5 / x = 10
Simplifying this equation, we get:
7.29x + 182.25 = 10x + 725
2.71x = 542.75
x ≈ 200
Therefore, the speed of the car on unpaved roads is 200 km/h, and the speed of the car on paved roads is 225 km/h (x + 25).
Step-by-step explanation:
Please help. Assignment overdue :(
PLEASE SHOW WORK!

Answers
Answer:
x=2
UO=16
sorry im not sure what the 3rd question is asking
Step-by-step explanation:
8x-3x=5x
5x=10
x=2
8(2)=16
In your opinion, what components of a free market are the most important
Answers
A free market is one where voluntary exchange and the laws of supply and demand provide the sole basis for the economic system, without government intervention. A key feature of free markets is the absence of coerced (forced) transactions or conditions on transactions.
Find the product of 32 and 46. Now reverse the digits and find the product of 23 and 64. The products are the same!
Does this happen with any pair of two-digit numbers? Find two other pairs of two-digit numbers that have this property.
Is there a way to tell (without doing the arithmetic) if a given pair of two-digit numbers will have this property?
Answers
Let's calculate the products and check if they indeed have the same value:
Product of 32 and 46:
32 * 46 = 1,472
Reverse the digits of 23 and 64:
23 * 64 = 1,472
As you mentioned, the products are the same. This phenomenon is not unique to this particular pair of numbers. In fact, it occurs with any pair of two-digit numbers whose digits, when reversed, are the same as the product of the original numbers.
To find two other pairs of two-digit numbers that have this property, we can explore a few examples:
Product of 13 and 62:
13 * 62 = 806
Reversed digits: 31 * 26 = 806
Product of 17 and 83:
17 * 83 = 1,411
Reversed digits: 71 * 38 = 1,411
As for determining if a given pair of two-digit numbers will have this property without actually performing the multiplication, there is a simple rule. For any pair of two-digit numbers (AB and CD), if the sum of A and D equals the sum of B and C, then the products of the original and reversed digits will be the same.
For example, let's consider the pair 25 and 79:
A = 2, B = 5, C = 7, D = 9
The sum of A and D is 2 + 9 = 11, and the sum of B and C is 5 + 7 = 12. Since the sums are not equal (11 ≠ 12), we can determine that the products of the original and reversed digits will not be the same for this pair.
Therefore, by checking the sums of the digits in the two-digit numbers, we can determine whether they will have the property of the products being the same when digits are reversed.