Solve the equation. -z/4 = -3/4
Answers
answer
-z•1=-3-1
z=-3•-1
z=3
Related Questions
Given: ,
bisects ∠AEC.
A horizontal line has points A, E, D. 2 lines extend from point E. One line extends to point B and another extends to point C. A small box represents the angle for C E D.
What statements are true regarding the given statement and diagram?
∠CED is a right angle.
∠CEA is a right angle.
m∠CEA = One-half(m∠CEB)
m∠CEB = m∠BEA
m∠DEB = 135°
m∠AEB = 35°
Answers
Answer:
angle ced is a right ange
so the m angels debate =135 m angle aeb =35
so the answer is 135+35 =170
180 is a all side sim
=180-170=10 answer
Answer:
∠CED is a right angle.
∠CEA is a right angle.
m∠CEB = m∠BEA
m∠DEB = 135°
For positive integer n, the factorial notation n! represents the product of the integers from n to 1. (For example, 6!= 6.5.4.3. 2. 1.) What value of N satisfies the following equation? 5!.9!= 12. N! (A)10 (B)11 (C)12 (D)13 (E)14
Answers
The value of N that satisfies the following equation, 5!9!= 12N!, is 10.
Factorial notation (n!) means to multiply a series of descending natural numbers. Also stated in the problem that for positive integer n, the factorial notation n! represents the product of the integers from n to 1.
Take for example 6! which can be written as 6 x 5 x 4 x 3 x 2 x 1 = 720.
Given the equation 5!9!= 12N!, expand the factorial notation.
(5 x 4 x 3 x 2 x 1)(9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) = (4 x 3) N!
N! = (5 x 2 x 1)(9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1)
N! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
N = 10
Therefore, the value of N that satisfies the following equation, 5!9!= 12N!, is 10.
Learn more about factorial here: https://brainly.com/question/16868621
#SPJ4
HELP MEEE ‼️‼️‼️ MATH IS HARD.

Answers
The answer to the following are below:
Total water area for Alabama and Florida = 2.9 × 10⁷
Total water area for Hawaii and Michigan = 8.5 × 10⁷
Difference of water area of Florida and Hawaii = 3.3 × {10}^{- 1}
Difference of water area of Michigan and Alabama = 2.3 × 10¹
What is the total water area?Alabama = 1.7 × 10³
Florida = 1.2 × 10⁴
Hawaii = 4.5 × 10³
Michigan = 4.0 × 10⁴
Total water area for Alabama and Florida = (1.7 × 10³) + (1.2 × 10⁴)
= (1.7 + 1.2) × {10}^{3 + 4}
= 2.9 × 10⁷
Total water area for Hawaii and Michigan = (4.5 × 10³) + (4.0 × 10⁴)
= (4.5 + 4.0) × {10}^{3 + 4}
= 8.5 × 10⁷
Difference of water area of Florida and Hawaii = (4.5 × 10³) - (1.2 × 10⁴)
= (4.5 - 1.2) × {10}^{3 - 4}
= 3.3 × {10}^{- 1}
Difference of water area of Michigan and Alabama = (4.0 × 10⁴) - (1.7 × 10³)
= (4.0 - 1.7) × {10}^{4 - 3}
= 2.3 × 10¹
Read more on exponents:
https://brainly.com/question/13669161
#SPJ1
an electrician completes 1/6 of a job in 2/3 hour. At this rate, how long does it take the electrician to complete the job?
Answers
Answer:
It takes the electrician 4 hours to complete the job
Step-by-step explanation:
This question can be solved using a rule of three.
In 2/3 of an hour, he completes a sixth of a job. So how many hours does it take for him to complete the job(which is 100% = 6/6 = 1)?
2/3 hour - 1/6 of the job
x hours - 1 of the job
\(\frac{1}{6}x = \frac{2}{3}\)
Applying cross multiplication
\(3x = 6*2\)
\(3x = 12\)
\(x = \frac{12}{3}\)
\(x = 4\)
It takes the electrician 4 hours to complete the job
Based on the graph how many bottles will be filled in 80 seconds? 

Answers
Answer:
Below
Step-by-step explanation:
Find unit rate (since it starts at 0,0)
at 45 seconds it is 900 bottles
900 bottles / 45 seconds = 20 bottle / sec
20 bottles / sec * 80 sec = 1600 bottles
Select the correct answer. What is the average rate of change of f(x), represented by the table of values, over the interval [-3, 4]? x f(x) -6 27 -3 6 -1 2 0 3 1 6 4 27 A. -6 B. -3 C. 3 D. 6 E. 21
Answers
The average rate of change of f(x), represented by the table is 1/7
Rate of change of expressionThe formula for calculating the rate of change which is also known as the slope is expressed as;
Rate of change = f(b)-f(a)/b-a
Using the interval [-3 4]
f(b) = f(4) = 7
f(x) = f(-3) = 6
Substitute
Rate of change = 7-6)/4-(-3)
Rate of change= 1/7
Hence the average rate of change of f(x), represented by the table is 1/7
Learn more on rate of change here: https://brainly.com/question/8728504
#SPJ1
EX 1) Games Galore Super Store buys the latest video game at a wholesale price of $30.00. The markup rate at Game's Galore Super Store is 40%. You use your allowance to purchase the game at the store. How much will you pay, not including tax?
Answers
Answer:
$42
Step-by-step explanation:
Given that,
Galore Super Store buys the latest video game at a wholesale price of $30.00.
The markup rate at Game's Galore Super Store is 40%.
We need to find the price from the store. It can be calculated as follows :
\(C=30+\dfrac{40}{100}\times 30\\\\=30+12\\\\=\$42\)
Hence, we will pay $42.
express 2 cos 35 sin 67 as a sum
Answers
2 cos 35 sin 67 can be expressed as the sum of sin(102) and -sin(32).
To express 2 cos 35 sin 67 as a sum, we can use the trigonometric identity for the product of two sine or cosine functions.
Specifically, the identity states that 2 cos A sin B can be written as
sin(A + B) + sin(A - B).
Applying this identity, we have:
2 cos 35 sin 67 = sin(35 + 67) + sin(35 - 67)
Simplifying the expressions inside the sine functions:
sin(102) + sin(-32)
Since the sine function is an odd function,
sin(-x) = -sin(x),
so we can rewrite the equation as:
sin(102) - sin(32)
Therefore, 2 cos 35 sin 67 can be expressed as the sum of sin(102) and -sin(32).
For such more questions on trigonometric identity
https://brainly.com/question/7331447
#SPJ8
. A foreman for an injection-molding firm admits that on 23% of his shifts, he forgets to shut off the injection machine on his line. Failure to shut down at night causes the machine to overheat, increasing the probability that a defective molding will be produced during the early morning run from 5% to 15%. The plant manager randomly selects a molding from the early morning run and discovers it is defective. What is the probability that the foreman forgot to shut off the machine the previous night?
Answers
Answer:
P(F | D) = 47.26%
There is a 47.26% probability that the foreman forgot to shut off the machine the previous night.
Step-by-step explanation:
A foreman for an injection-molding firm admits that on 23% of his shifts, he forgets to shut off the injection machine on his line.
Let F denote the event that foreman forgets to shut off the machine.
Failure to shut down at night causes the machine to overheat, increasing the probability that a defective molding will be produced during the early morning run from 5% to 15%.
Let D denote the event that the mold is defective.
If the foreman forgets to shut off the machine then 15% molds get defective.
P(F and D) = 0.23×0.15
P(F and D) = 0.0345
If the foreman doesn't forget to shut off the machine then 5% molds get defective.
P(F' and D) = (1 - 0.23)×0.05
P(F' and D) = 0.77×0.05
P(F' and D) = 0.0385
The probability that the mold is defective is
P(D) = P(F and D) + P(F' and D)
P(D) = 0.0345 + 0.0385
P(D) = 0.073
The probability that the foreman forgot to shut off the machine the previous night is given by
∵ P(B | A) = P(A and B)/P(A)
For the given case,
P(F | D) = P(F and D)/P(D)
Where
P(F and D) = 0.0345
P(D) = 0.073
So,
P(F | D) = 0.0345/0.073
P(F | D) = 0.4726
P(F | D) = 47.26%
Please look at the image

Answers
Answer:
m<E = 60 deg
Step-by-step explanation:
The sum of the measures of the angles of a triangle is 180 deg.
m<E + m<F + m<G = 180
m<E + 75 + 45 = 180
m<E + 120 = 180
m<E = 60
Answer:
60 is the ans
Step-by-step explanation:
let angle E be x
then add all sides of triangle and subtract it from 180 you will get 60 degree as ans
Find the value of x. assume that segments that appear to be tangent are tangent.

Answers
Answer:
9
Step-by-step explanation:
The explanation is in the picture

The amount of CO2 emitted per year A (in tons) for a vehicle that averages x miles per gallon of gas, can
be approximated by the function A(x) = 0.0089x2 – 0.815x + 22.3.
a) Determine the average rate of change of the amount of CO2 emitted in a year over the interval
[20, 25), and interpret its meaning.
Answers
Answer:
Average Rate of Change = -0.4145
It means that the amount of CO2 emitted per year will decrease by an averaage rate of 0.4145 (tons - gallon of gas)/mile
Step-by-step explanation:
In order to solve this problem, we can make use of the Average Rate of Change formula, which looks like this:
\(ARC=\frac{A(25)-A(20)}{25-20}\)
So we need to start by finding what A(25) is equal to, so we get:
\(A(25)= 0.0089(25)^{2}-0.0815(25)+22.3\)
so
A(25)=7.4875
next, we can find A(20)
\(A(20)=0.0089(20)^{2}-0.0815(20)+22.3\)
so we get:
A(20)=9.56
so now we can use the average rate of change formula:
\(ARC=\frac{A(25)-A(20)}{25-20}\)
\(ARC=\frac{7.4875-9.56}{25-20}\)
ARC=-0.4145
and It means that the amount of CO2 emitted per year will decrease by an averaage rate of 0.4145 (tons - gallon of gas)/mile
Select the shapes that are similar to shape A.
Answers
Answer:
I'm sorry but I cannot help you because you have not put a picture
In a clinical test with 2161 subjects, 1214 showed improvement from the treatment. Find the margin of error for the 95% confidence interval used to estimate the population proportion.
Answers
Answer:
The margin of error for the 95% confidence interval used to estimate the population proportion is of 0.0209.
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the z-score that has a p-value of \(1 - \frac{\alpha}{2}\).
The margin of error is of:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In a clinical test with 2161 subjects, 1214 showed improvement from the treatment.
This means that \(n = 2161, \pi = \frac{1214}{2161} = 0.5618\)
95% confidence level
So \(\alpha = 0.05\), z is the value of Z that has a p-value of \(1 - \frac{0.05}{2} = 0.975\), so \(Z = 1.96\).
Margin of error:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
\(M = 1.96\sqrt{\frac{0.5618*0.4382}{2161}}\)
\(M = 0.0209\)
The margin of error for the 95% confidence interval used to estimate the population proportion is of 0.0209.
plz help me with this

Answers
Answer:
\((x,y) = (-1,-2.5)\)
Step-by-step explanation:
Let be \(f(x) = \frac{(x+3)^{2}}{x-2}\) and \(g(x) = \left|\frac{x}{2}\right| -3\), we plot each curve with the help of graphic tool. In this case, we use Desmos and outcome is presented in the image attached below. Mathematically speaking, a solution to the system of equation exists when \(f(x) = g(x)\). Graphically speaking, it means that a solution exists when both curves pass through each other.
According to the graphic tool, we conclude that the only solution to the system of equations is \((x,y) = (-1,-2.5)\).

12 / 0.96 please answer this i need it
Answers
Answer:
12.5
Step-by-step explanation:
Moses receives a gift that is wrapped in a cube shaped box. The volume of the box is 1331/8 cubic inches.Find the length of a side of the box
Answers
Answer:
5.5inches
Step-by-step explanation:
1331/8=166.375
then length of a side is = cubic root of 166.375
=³√166.375
5.5
Round 5,619 to the nearest thousand.
Answers
Answer:
6,000
Step-by-step explanation:
Since we round to the thousand we look at the place behind there. Since 6 is in the hundreds place we have to round the number up. Meaning that we will round to 6,000.
Answer:
6000
Step-by-step explanation:
Identity the thousandth digit
Then look at the digit, next to the thousandth place. If that digit is less than 5,you then round down to the thousandth digit,but If that digit is greater than or equal to 5, you round up the thousandth digit.
How do you interpret domain and range in terms of the context?
Answers
Answer:
By the end of this resource, you will be able to identify domain and range from any given contextual situation.
Determining the domain and range from a linear or quadratic contextual situation is similar to determining the independent and dependent variables.
Step-by-step explanation:
Suppose you are interviewing for a job. Your employer offers you the choice of two different options for your pay. The first option is to pay you $10.00 per hour and give you a raise of $.50 per hour at the end of the year. The second option is to pay you $11.50 per hour and give you a raise of $.25 per hour at the end of the year.
First, find a function for each option. To do that, you have to know what the domain and range might be. Let y = the amount you will make at the end of the year and x = the number of hours you work. Thinking about what would be reasonable values for x and y will help determine the domain and range.
First, let's think about the domain. Since x represents the numbers of hours you worked for the year, would it be reasonable to have negative values? If you said NO, you would be correct. We can assume the lowest possible value in the domain would equal zero. So, our domain would be {x| x ≥ 0}.
Now, let’s think about the range. Since y represents your earnings at the end of the year, would it be reasonable to have negative values? If you said NO again, you would be correct. You cannot earn a negative amount. We can assume the lowest possible value in the range would also equal zero. So, our range would be {y | y ≥ 0}. You should be able to relate with this situation since you may have to make a decision in comparing two or more job offers in your future.
It's important to realize that every situation is different and you must think about what is reasonable.
What is the meaning of "an axiom of predicate calculus"?

Answers
An axiom of predicate calculus is the foundation of predicate calculus that is based on a fundamental and obvious principle or statement
What is the axiom of calculus?The foundation of predicate calculus is based on a fundamental and obvious principle or statement known as an axiom.
The aforementioned axioms act as a foundation for deducing rational conclusions and evidence within the domain of predicate calculus.
Universally accurate and accepted without the need for additional reasoning is how they are commonly perceived.
The fundamental regulations and connections that oversee quantifiers, predicates, and logical operations, including conjunction, disjunction, and implication, are determined by the axioms of predicate calculus. They offer a sturdy groundwork for rationalizing statements that involve variables, quantification, and logical connectors in formal systems of logic.
Learn more about calculus at: https://brainly.com/question/24430269
#SPJ1
write the equation of the circle in standard form: Center: (-6,2), area: pi
Answers
\(\textit{area of a circle}\\\\ A=\pi r^2 ~~ \begin{cases} r=radius\\[-0.5em] \hrulefill\\ A=\pi \end{cases}\implies \pi =\pi r^2\implies \cfrac{\pi }{\pi }=r^2 \\\\\\ 1=r^2\implies \sqrt{1}=r\implies 1=r\)
so we're really looking for the equation of a circle with a radius of 1 and with a center at (-6 , 2)
\(\textit{equation of a circle}\\\\ (x- h)^2+(y- k)^2= r^2 \hspace{5em}\stackrel{center}{(\underset{-6}{h}~~,~~\underset{2}{k})}\qquad \stackrel{radius}{\underset{1}{r}} \\\\[-0.35em] ~\dotfill\\\\ ( ~~ x - (-6) ~~ )^2 ~~ + ~~ ( ~~ y-2 ~~ )^2~~ = ~~1^2\implies (x+6)^2 + (y-2)^2=1\)
Suppose that a box contains 8 cameras and that 4 of them are defective. A sample of 2 cameras is selected at random. Define the random variable variable x as the number of defective cameras in the sample. What is the probability distribution for x?
Answers
The probability distribution for x is:
x P(x)
0 0.214
1 0.571
2 0.214
How can we determine the probability distribution for x?Since there are 8 cameras in the box, the total number of ways to choose 2 cameras from the box is given by the combination formula:
C(8,2) = 8!/(2!×(8-2)!) = 28
So there are 28 possible ways to choose a sample of 2 cameras.
Now, let's calculate the probability of each possible value of x:
When x = 0, both cameras in the sample are non-defective. The number of ways to choose 2 non-defective cameras from the 4 non-defective cameras in the box is given by the combination formula:
C(4,2) = 4!/(2!×(4-2)!) = 6
So the probability of x = 0 is:
P(x=0) = (number of ways to choose 2 non-defective cameras)/(total number of ways to choose 2 cameras)
= 6/28
= 0.214
When x = 1, one camera in the sample is defective and the other is non-defective. The number of ways to choose 1 defective camera from the 4 defective cameras in the box and 1 non-defective camera from the 4 non-defective cameras in the box is given by the product of the corresponding combinations:
C(4,1) × C(4,1) = 4×4 = 16
So the probability of x = 1 is:
P(x=1) = (number of ways to choose 1 defective camera and 1 non-defective camera)/(total number of ways to choose 2 cameras)
= 16/28
= 0.571
When x = 2, both cameras in the sample are defective. The number of ways to choose 2 defective cameras from the 4 defective cameras in the box is given by the combination formula:
C(4,2) = 4!/(2!×(4-2)!) = 6
So the probability of x = 2 is:
P(x=2) = (number of ways to choose 2 defective cameras)/(total number of ways to choose 2 cameras)
= 6/28
= 0.214
Therefore, the probability distribution for x is:
x P(x)
0 0.214
1 0.571
2 0.214
to know more about probability
brainly.com/question/30034780
#SPJ1
Help me pls will give out points

Answers
\(y = ab^{x} \)
\(y = 3 \times {4}^{x} \)
"a" is the initial amount (3), and "b" is the growth factor (4).
To find "b" plug in the knowns into the exponential function equation and solve.
\(y = ab^{x} \)
\(48 = 3 \times {b}^{2} \)
\(16 = {b}^{2} \)
\( \sqrt{16} = b\)
\(b = 4\)
b is the midpoint of segment ac. a has coordinates (-3, 4) and b has coordinates (-1 1/2, 1). find the coordinates of c
Answers
The coordinates point C of the given line segment AC is C(0, -2) whose midpoint is at B.
How to calculate a midpoint of a line segment?To calculate the midpoint of a line segment, find the average for the coordinates of the endpoints of the line segment. I.e.,
Consider a line segment AC, B is its midpoint.
So, the coordinates of B are (Where we have A(x1, y1) and C(x2, y2))
B(x, y) = \((\frac{x1+x2}{2}, \frac{y1+y2}{2})\)
Calculation:It is given that, B is the midpoint of a line segment AC.
Where A has coordinates as (-3, 4) and B has coordinates as (-1 1/2, 1).
So, the coordinates of the other end point C of the given line segment are calculated as
B(x, y) = \((\frac{x1+x2}{2}, \frac{y1+y2}{2})\)
⇒ (-1.5, 1) = \((\frac{-3+x2}{2}, \frac{4+y2}{2})\)
⇒ -1.5 = (-3 + x2)/2 and 1 = (4 + y2)/2
⇒ -3 = -3 + x2 and 2 = 4 + y2
⇒ x2 = 0 and y2 = 2 - 4 = -2
Therefore, point C has coordinates as (0, -2).
Learn more about calculating the midpoint here:
https://brainly.com/question/5566419
#SPJ4

Question 3 (5 points)
(02.01 MC)
Which of these is a positive externality of carpooling with friends to work?
оа
Reduced commute time
Ob
Reduced driving focus
Ос
Reduced traffic on the road
Od
Reduced time to socialize
Answers
Answer:
reduced traffic on the road
Step-by-step explanation:
just took the test :)
Answer: C) Reduced traffic on the road
Step-by-step explanation: Ive taken this test
1x²- 16x = 20 is mg questions
Answers
The solutions to the equation 1x² - 16x = 20 are x = 8 + 2√21 and x = 8 - 2√21.
To solve the quadratic equation 1x² - 16x = 20, we need to rearrange it into the standard form ax² + bx + c = 0. Let's simplify the equation step by step:
1x² - 16x = 20
First, move all terms to one side of the equation:
1x² - 16x - 20 = 0
Now we have a quadratic equation in the standard form. To solve it, we can use factoring, completing the square, or the quadratic formula. In this case, factoring may not be straightforward, so let's use the quadratic formula:
x = (-b ± √(b² - 4ac)) / (2a)
For our equation, a = 1, b = -16, and c = -20. Substituting these values into the quadratic formula:
x = (-(-16) ± √((-16)² - 4(1)(-20))) / (2(1))
Simplifying further:
x = (16 ± √(256 + 80)) / 2
x = (16 ± √336) / 2
x = (16 ± √(16 * 21)) / 2
x = (16 ± 4√21) / 2
Simplifying:
x = 8 ± 2√21
For more such questions on solutions
https://brainly.com/question/17145398
#SPJ8
Please help. I’ll mark you as brainliest if correct!

Answers
Answer:
Since we are talking annual interest and, I assume a time period of 1 year:
The interest earned is the sum of the interest earned on the two loans separately
Let x = amount loaned at 14%
18,500-x = amount loaned at 12%
I = prt
p = x and 18500-x
r = 0.14 and 0.12
t = 1
2390 = 0.14x + 0.1(18500-x)
2390 = .14x + 1850 - 0.1x
x = 13500
x = $13,500 loaned at 14%
18500-x = $5,000 loaned at 12%
Answer:
$8,500 was loaned at 14%, and
$10,000 was loaned at 12%.
Step-by-step explanation:
Total loan: $18,500.
Part at 14%
Part at 12%
Let the part at 14% = x.
Let the part at 12% = y.
Equation of amount of loan:
x + y = 18500
x amount at 14% earns 14% of x = 0.14x interest.
y amount at 12% earns 12% of y = 0.12y interest.
Equation of interest charged:
0.14x + 0.12y = 2390
We have a system of equations.
x + y = 18500
0.14x + 0.12y = 2390
Multiply both sides of the first equation by -0.12. Write the second equation below it, and add the equations.
-0.12x - 0.12y = -2220
(+) 0.14x + 0.12x = 2390
-------------------------------------
0.02x = 170
x = 170/0.02
x = 8500
x + y = 18,500
8500 + y = 18,500
y = 10,000
Answer:
$8,500 was loaned at 14%, and
$10,000 was loaned at 12%.
attachemnt
look at it
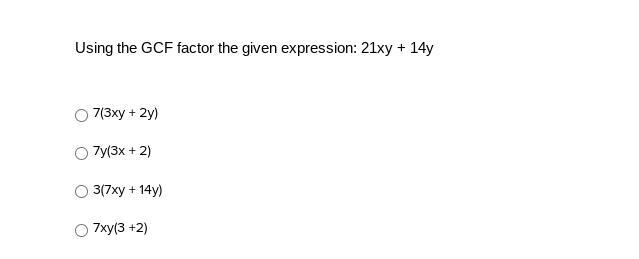
Answers
Answer: 7y(3x+2)
Step-by-step explanation:
The greatest-common-factor for the coefficients 21 and 14 is 7
Both 21xy and 14y have the variable y
So the GCF factor is 7y
At the local Theatre of the Arts, tickets cost $4 for children and $5 for adults. In the opening Saturday night of a play, the theater made $540. The second day was a matinee and the prices were lower for children at $3 and the same price as Saturday for adults. They made $440 at the matinee.
A) Write a system of equations in standard form that represents the prices at the Theatre on Saturday and the second day.
B) Rewrite the system of equations in slope-intercept form. What are the y-intercepts of both equations?
Answers
A. The system of equations in standard form is: 4x + 5y = 540 and 3x + 5y = 440.
B. The y-intercept of the equation representing the prices on Saturday night is 108, and the y-intercept of the equation representing the prices at the matinee on the second day is 88.
A) Let's define the variables:
Let x represent the number of children attending.
Let y represent the number of adults attending.
On Saturday night:
The equation for the revenue generated on Saturday night is:
4x + 5y = 540 (since children's tickets cost $4 and adults' tickets cost $5, and the total revenue is $540).
Matinee on the second day:
The equation for the revenue generated at the matinee is:
3x + 5y = 440 (since children's tickets cost $3 and adults' tickets still cost $5, and the total revenue is $440).
Therefore, the system of equations in standard form is:
4x + 5y = 540
3x + 5y = 440
B) Let's rewrite the system of equations in slope-intercept form:
On Saturday night:
4x + 5y = 540
Rearranging the equation, we get:
5y = -4x + 540
Dividing both sides by 5, we get:
y = (-4/5)x + 108
The y-intercept of this equation is 108.
Matinee on the second day:
3x + 5y = 440
Rearranging the equation, we get:
5y = -3x + 440
Dividing both sides by 5, we get:
y = (-3/5)x + 88
The y-intercept of this equation is 88.
For such more question on equation:
https://brainly.com/question/17145398
#SPJ8
Evan has $0.45 worth of pennies and nickels. He has a total of 21 pennies and nickels altogether. Determine the number of pennies and the number of nickels that Evan has.