T/F : A determinant of an nÃn matrix can be defined as a sum of multiples of determinants of (nâ1)Ã(nâ1) submatrices.
Answers
True. The determinant of an n x n matrix can be defined as a sum of multiples of determinants of (n-1) x (n-1) submatrices, which are called the minors of the matrix.
The determinant of an n x n matrix can be defined as a sum of multiples of determinants of (n-1) x (n-1) submatrices, which are called the minors of the matrix.
More specifically, let A be an n x n matrix with entries a_ij. The determinant of A, denoted by det(A), can be defined recursively as follows:
- If n = 1, then det(A) = a_11.
- If n > 1, then det(A) = sum((-1)^(i+j) * a_ij * det(A_ij)), where the sum is taken over the first row or first column of A. Here, A_ij denotes the (n-1) x (n-1) submatrix obtained by deleting the i-th row and j-th column of A.
This recursive definition shows that the determinant of an n x n matrix can be expressed as a sum of (n-1) x (n-1) determinants of submatrices, with appropriate signs and coefficients. This is known as the cofactor expansion of the determinant along the first row or first column of the matrix.
Visit to know more about Matrix:-
brainly.com/question/2456804
#SPJ11
Related Questions
flights with o-ring damage 43 57 58 63 70 70 75 flights with no o-ring damage 66 67 67 67 68 69 70 70 72 73 75 76 76 78 79 81 is the mean launch temperature for flights with o-ring damage significantly less than for flights with no o-ring damage? use 5% level of significance.
Answers
To determine if the mean launch temperature for flights with o-ring damage is significantly less than for flights with no o-ring damage, we can perform a two-sample t-test with equal variances. Here are the steps:
Step 1: Calculate the sample means and standard deviations for each group:
For flights with o-ring damage:
Sample mean: (43 + 57 + 58 + 63 + 70 + 70 + 75) / 7 = 63.14
Sample standard deviation: 13.42
For flights with no o-ring damage:
Sample mean: (66 + 67 + 67 + 67 + 68 + 69 + 70 + 70 + 72 + 73 + 75 + 76 + 76 + 78 + 79 + 81) / 16 = 72.56
Sample standard deviation: 5.69
Step 2: Calculate the pooled standard deviation:
s_p = sqrt(((n1-1)*s1^2 + (n2-1)*s2^2) / (n1+n2-2))
where:
n1 = sample size of flights with o-ring damage = 7
n2 = sample size of flights with no o-ring damage = 16
s1 = sample standard deviation of flights with o-ring damage = 13.42
s2 = sample standard deviation of flights with no o-ring damage = 5.69
s_p = sqrt(((7-1)*13.42^2 + (16-1)*5.69^2) / (7+16-2)) = 9.88
Step 3: Calculate the t-test statistic:
t = (x1 - x2) / (s_p * sqrt(1/n1 + 1/n2))
where:
x1 = sample mean of flights with o-ring damage = 63.14
x2 = sample mean of flights with no o-ring damage = 72.56
s_p = pooled standard deviation = 9.88
n1 = sample size of flights with o-ring damage = 7
n2 = sample size of flights with no o-ring damage = 16
t = (63.14 - 72.56) / (9.88 * sqrt(1/7 + 1/16)) = -2.70
Step 4: Calculate the degrees of freedom:
df = n1 + n2 - 2 = 7 + 16 - 2 = 21
Step 5: Determine the critical value of t at 5% level of significance and the corresponding p-value:
At 5% level of significance and 21 degrees of freedom, the critical value of t is ±2.08 (from a t-distribution table or calculator).
The p-value for a two-tailed test with t = -2.70 and df = 21 is 0.013 (from a t-distribution table or calculator).
Step 6: Compare the t-test statistic with the critical value and the p-value with the level of significance:
Since the absolute value of the t-test statistic (-2.70) is greater than the critical value of t at 5% level of significance (2.08), we reject the null hypothesis and conclude that there is a significant difference in mean launch temperature between flights with o-ring damage and flights with no o-ring damage.
Moreover, the p-value (0.013) is less than the level of significance (0.05), providing further evidence to reject the null hypothesis.
Therefore, we can say that the mean launch temperature for flights with o-ring damage is significantly less.
If g (x)=3x-7, then g(4)=
Answers
Answer:
To find the inverse of g(x) we need to interchange x and y, as follows:
y = 3x - 7
x = 3y -7
3y = x + 7
Step-by-step explanation:
YOUR WELCOME
\(\qquad\qquad\huge\underline{\boxed{\sf Answer☂}}\)
To find g(4), we have to substitute the variable x with 4 on the expression g(x) ~
\(\qquad \sf \dashrightarrow \: g(x) = 3x - 7\)
\(\qquad \sf \dashrightarrow \: g(4) = 3(4)- 7\)
\(\qquad \sf \dashrightarrow \: g(4) = 12- 7\)
\(\qquad \sf \dashrightarrow \: g(4) =5\)
Consider the standard form equation Ax+By=−24. If the x-intercept is (−3,0) and the y-intercept is (0,12), what are the values of A and B?
Answers
Answer:
A = 8 and B = -2 and the equation is:
8x - 2y = -24
Step-by-step explanation:
Line intercepts
Any non-horizontal and non-vertical line has two intercepts: The y-intercept is the point where the line crosses the y-axis, and the x-intercept is the point where the line crosses the x-axis, also called the zero or root.
We are given the equation:
Ax+By=-24
The x-intercept is (-3,0). Substituting the values of x and y:
A(-3)+B(0)=-24
Operating:
-3A = -24
Dividing by -3:
A = -24 / (-3) = 8
A = 8
The y-intercept is (0,12). Substituting and using the just-found value of A
8(0)+B(12)=-24
Operating:
12B = -24
Solving:
B = -2
Thus, A = 8 and B = -2 and the equation is:
8x - 2y = -24
Please help!! Will give brainliest

Answers
Answer:
The first choice
Step-by-step explanation:
7/8 x + 3/4 = -6
6 (x/8) + 3/4 = -6
What is an expression that can be use to multiply 6 x 198 mentally?
Answers
Answer:
paper and pencil
Step-by-step explanation:
get a paper then a pencil and solve it
-6 × 2 + 6 × 200.
Hope this helps! :D - your friendly neighborhood Jxro!
The coordinates of C are (0.96, 0.28).
What are cos(A) and sin(A)? Explain how you know.
Answers
The values of cos(A) and sin(A) are cos(A) = 0.96 and sin(A) = 0.28
How to determine the values of cos(A) and sin(A)?From the question, we have the following parameters that can be used in our computation:
The coordinates of C are (0.96, 0.28).
In a unit circle,
(x, y) = (cos, sin)
Using the above as a guide, we have the following:
x = 0.96
y - 0.28
This means that
cos(A) = 0.96
sin(A) = 0.28
Hence, the values of cos(A) and sin(A) are cos(A) = 0.96 and sin(A) = 0.28
Read more about unit circle at
https://brainly.com/question/20691579
#SPJ1
HELP PLEASE I HAVE A TIME LIMIT
the net for a pentagonal prism has 7 regions and 10 vertices. use Euler's formula to find the number of segments
Answers
Using the Euler's formula, the number of segments in the pentagonal prism is: 15.
What is the Euler's Formula?The Euler's formula is given as, F + V = E + 2, where:
F = number of faces (number of regions)V = verticesE = number of edges (number of segments).Given that the pentagonal prism has the following dimensions:
F = 7V = 10E = number of segments = ?Plug in the values into the Euler's formula, F + V = E + 2:
7 + 10 = E + 2
17 - 2 = E
E = 15
Therefore, using the Euler's formula, the number of segments in the pentagonal prism is: 15.
Learn more about the Euler's formula on:
https://brainly.com/question/1178790
An object was launched off the top of a building. The function f(x)=-16x^2+16x+672 represents the height of the object above the ground, in feet, x seconds after being launched. Find and interpret the given function values and determine an appropriate domain for the function.
Answers
Answer:
6x2 + 16x = 672
Reorder the terms:
16x + 16x2 = 672
Solving
16x + 16x2 = 672
Solving for variable 'x'.
Reorder the terms:
-672 + 16x + 16x2 = 672 + -672
Combine like terms: 672 + -672 = 0
-672 + 16x + 16x2 = 0
Factor out the Greatest Common Factor (GCF), '16'.
16(-42 + x + x2) = 0
Factor a trinomial.
16((-7 + -1x)(6 + -1x)) = 0
Ignore the factor 16.
Subproblem 1
Set the factor '(-7 + -1x)' equal to zero and attempt to solve:
Simplifying
-7 + -1x = 0
Solving
-7 + -1x = 0
Move all terms containing x to the left, all other terms to the right.
Add '7' to each side of the equation.
-7 + 7 + -1x = 0 + 7
Combine like terms: -7 + 7 = 0
0 + -1x = 0 + 7
-1x = 0 + 7
Combine like terms: 0 + 7 = 7
-1x = 7
Divide each side by '-1'.
x = -7
Simplifying
x = -7
Subproblem 2
Set the factor '(6 + -1x)' equal to zero and attempt to solve:
Simplifying
6 + -1x = 0
Solving
6 + -1x = 0
Move all terms containing x to the left, all other terms to the right.
Add '-6' to each side of the equation.
6 + -6 + -1x = 0 + -6
Combine like terms: 6 + -6 = 0
0 + -1x = 0 + -6
-1x = 0 + -6
Combine like terms: 0 + -6 = -6
-1x = -6
Divide each side by '-1'.
x = 6
Simplifying
x = 6
Solution
x = {-7, 6}
Step-by-step explanation:
The given quadratic function models the projectile of the object as it is
launched off the top of the building.
The interpretation of the function values are;
The maximum height reached by the object is 676 feetThe height of the building is 672 feetTime of flight of the object is 7 secondsThe appropriate domain is 0 ≤ x ≤ 7
Reasons:
The given function for the height of the object is f(x) = -16·x² + 16·x + 672
The domain is given by the values of x for which the value of y ≥ 0
Therefore, when -16·x² + 16·x + 672 = 0, we get;
-16·x² + 16·x + 672 = 0
16·(-x² + x + 42) = 0
-x² + x + 42 = 0
x² - x - 42 = 0
(x - 7)·(x + 6) = 0
x = 7, or x = -6
The minimum value of time, x is 0, which is the x-value at the top of the
building, and when x = 7, the object is on the ground.
Therefore;
The appropriate domain is 0 ≤ x ≤ 7The maximum value of f(x) = a·x² + b·x + c, is given at \(x = -\dfrac{b}{2 \cdot a}\)
Therefore;
We have;
\(x = -\dfrac{16}{2 \times (-16)} = \dfrac{1}{2}\)
Which gives;
\(f \left(\frac{1}{2} \right) = -16 \times \left(\dfrac{1}{2} \right)^2 + 16 \times \left(\dfrac{1}{2} \right)+ 672 = 676\)
The maximum height reached by the object, \(f\left(\frac{1}{2} \right)\) = 676 feetThe height of the building is given when the time, x = 0, as follows;
Height of building, f(0) = -16 × 0² + 16 × 0 + 672 = 672
The height of the building, f(0) = 672 feetLearn more here;
https://brainly.com/question/10837575
what's the ratio?
2 4 8 10
3
Answers
Answer:
is the order 2,4,8,10, and then 3?
or is it 2/3, 4/3, 8/3/ 10/3?
Step-by-step explanation:
square & cube numbers puzzle
| Using only square and cube numbers less than or equal to 100, can you fill in the circles to make these
| sums true? You can only use each number once and you must use all the numbers.
36) + (64
Square and cube numbers
Answers
Answer:
who friendhjcicivigigivigigogogig'g
PLEASE HELP!! Re-write the equation 3 x minus y = 4 in slope-intercept form.
a.
y = 3 x minus 4
c.
y = negative 3 x minus 4
b.
y = 3 x + 4
d.
y = negative 3 x + 4
Please select the best answer from the choices provided
A
B
C
D
Answers
Answer:
A) \(y = 3x - 4\)
Explanation:
Slope-intercept form is y = mx + b
The answer is A. y=3x-4
Slope intercept form formula:
y=mx+b
Solve for the angles in the triangle below.
A
70
B.
C
Blank #1 - what is angle y (where B is)?
Blank #2 - what is angle x (where C is)?

Answers
Answer:
y=70°(base angle of isosceles triangle)
in triangle ABC
70°+x°+y°=180°{sum of interior angle triangle}
70+x+70=180
x=180-140=40°
Step-by-step explanation:
x=40
y=70
carlos is using a hose to fill a bucket. the path of the water can be represented by the function f(t) where f(t) represents the height of the water in inches and t represents the time in seconds.
Answers
Answer:
The function represents the height of the water in the bucket
Step-by-step explanation:
Given
\(f(t) = -t^2 + 4t\)
Required
State what the function represents
From the question, we understand that t represents the time spent while the function illustrates the water level in the bucket.
This implies that f(t) calculates the height of the water in the bucket, given the value of time (t)
Hannah starting playing video games as soon as she got home from school. She played video games for 20 minutes. Then, it took Hannah 1 hour and 35 minutes to finish her homework. When Hannah finished her homework, it was 4:40 P.M. What time did Hannah get home from school?
Answers
Can someone help on this? Thank youu;)

Answers
Answer:
2^(3/7)
Step-by-step explanation:
For these types of questions, what is inside the root is the numerator, and what is on top is the denominator.
3 is in the root, so it is the numerator
7 is outside the root, so it is the denominator
Therefore, The answer is 2^(3/7)
Sam bought some apples at 60c each and sold all but 5 of them at R1,00 each. If he made a profit of R5,00, how many apples did he buy?
Answers
Answer:
5
Step-by-step explanation:
The number of apples bought by him is 113.
What is an expression?A grouping of variables, symbols, and/or numbers used to represent a mathematical quantity or relationship is known as an expression in mathematics. Expressions might be straightforward with just one number or variable or complex with many terms, operations, and functions.
Let's assume that Sam bought x number of apples.
He bought them at 60 cents each, which means the total cost of buying these apples was:
Cost price = 60x cents
He sold all but 5 of these apples at R1.00 each, which means the total revenue he earned from selling them was:
Revenue = (x - 5) x R1.00 = R(x - 5)
Sam made a profit of R5.00, which means his revenue was more than his cost price by R5.00. We can write this as:
Revenue - Cost price = R5.00
Substituting the values of revenue and cost price from above, we get:
R(x - 5) - 60x = 500 cents
Rearranging and simplifying this equation, we get:
40x = 500 + 5R
Substituting R = R1.00, we get:
40x = 500 + 5 = 505
Solving for x, we get:
x = 12.625
Since Sam cannot buy a fraction of an apple, we round up x to the nearest integer:
x = 13
To know more about an expression follow
https://brainly.com/question/15041862
#SPJ2
F(x)=x^2-4
g(x)=x-1
state all values of x which f(x)=g(x)
Answers
The values of x for which f(x) = g(x) are x = (1 + √13) / 2 and x = (1 - √13) / 2
To find the values of x for which f(x) is equal to g(x), we need to set the two functions equal to each other and solve for x.
Setting f(x) equal to g(x):
x^2 - 4 = x - 1
Rearranging the equation:
x^2 - x - 3 = 0
To solve this quadratic equation, we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
For our equation, a = 1, b = -1, and c = -3. Substituting these values into the quadratic formula:
x = (1 ± √((-1)^2 - 4(1)(-3))) / (2(1))
Simplifying further:
x = (1 ± √(1 + 12)) / 2
x = (1 ± √13) / 2
Therefore, the values of x for which f(x) = g(x) are:
x = (1 + √13) / 2
x = (1 - √13) / 2
For more such questions on values , Visit:
https://brainly.com/question/26352252
#SPJ11
A company needs a faster computer to enhance its e-business capabilities. the computer can be purchased for $1890 or rented for $900 plus $90 per month. what is the maximum number of months the computer could be kept so that it is cheaper to rent than to buy?
Answers
The maximum number of months the computer could be kept so that it is cheaper to rent than to buy is 10 months.
What is the maximum number of months?The first step is to determine the month in which the two options would have the same cost. The equation that can be used to determine this value is:
$1890 = $900 + 90t
90t = 1890 - 900
90t = 990
t = 990 / 90
t = 11 months
The maximum number of months = 11 months - 1 = 10 months
To learn more about division, please check: https://brainly.com/question/194007
#SPJ1
7 orders in 1 day =____ orders in 2 days
Answers
Answer:14 in 2 days
Step-by-step explanation:
-13+12p - 4 = 6(2p-1)
Answers
Answer:
\(-13+12p-4=6\left(2p-1\right)\)
\(-13-4=-17\)
\(12p-17=6\left(2p-1\right)\)
\(12p-17=12p-6\)
\(12p-17+17=12p-6+17\)
\(12p=12p+11\)
\(12p-12p=12p+11-12p\)
\(0=11\)
There is No Solution
The volume of this cone is 643,072 cubic inches. What is the radius of this cone?
Use ≈ 3.14 and round your answer to the nearest hundredth.
Answers
The radius of the cone is 783.84/√h
What is volume of a cone?A cone is the surface traced by a moving straight line (the generatrix) that always passes through a fixed point (the vertex).
Volume is defined as the space occupied within the boundaries of an object in three-dimensional space.
The volume of a cone is expressed as;
V = 1/3πr²h
643072 × 3 = 3.14 × r²h
r²h = 614400
r² = 614400/h
r = 783.84/√h
therefore the radius of the cone is 783.84/√h
learn more about volume of cone from
https://brainly.com/question/1082469
#SPJ1
is the pareto distribution a member of a location family? a member of a scale family? a member of a location-scale family? none of the above? explain.
Answers
Pareto distribution is a member of a scale family referring fixed values of the shape parameter, it is trivially closed under scale transformations.
The Pareto distribution is a power-law probability distribution used in description of social, quality control, scientific, geophysical, actuarial, and many other types of observable phenomena. It was initially applied to demonstrate the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The pareto principle or 80-20 rule states that 80% of outcomes are due to 20% of causes. Pareto distribution is a member of the scale family distribution which is parameterized by a scale parameter. The larger the scale parameter, the more spread out the distribution.
Learn more about Pareto distribution:
https://brainly.com/question/14785621
#SPJ4
UNIT 6: CEREAL BOX PROJECT / PORTFOLIO
A company has released the following possible designs for a new cereal box. The cost of production depends upon the cost of materials, which is determined by how much material is used. The amount of material used is equal to the surface area of the package plus some overlap. The amount of product contained in the package is the volume of the packaging.
Find the surface area and volume of the following possible cereal boxes. Determine the cost of making the cereal box assuming that cardboard costs $0.05 per square inch.

Answers
Answer:
DO you go to a connexus school? I do and i have this same project im trying to find answers to!
Step-by-step explanation:
For the first box the volume, surface area, and cost of materials are 180 cubic inches, 258 square inches, and $12.9, for the second box 192 cubic inches, 224.4 square inches, and $11.22 for the third box 235.61 cubic inches, 227.76 square inches, and $11.38.
What is volume?It is defined as a three-dimensional space enclosed by an object or thing.
For the first cereal box:
Volume = L×W×H
Here L = 7.5 in, W = 2 in, and H = 12 in
Volume = 7.5×2×12 = 180 cubic inches
Surface area = 2(L×B+B×H+H×L)
= 2(7.5×2+2×12+12×7.5)
= 2(15+24+90)
= 258 square inches
Cost for this cereal box = 258×0.05 = $12.9
For the second cereal box:
\(\rm Volume = \frac{1}{3} bh\)
b is the area and h, is the height of the pyramid.
b = 8×6 = 48 square inches, h = 12 inches
\(\rm Volume = \frac{1}{3} \times48\times12\)
Volume = 192 cubic inches
\(\rm Surface \ area = b+\frac{1}{2} ps\)
p is the perimeter of the base = 2(8+6) = 28 in
Slant height s = 12.6 in
\(\rm Surface \ area = 48+\frac{1}{2} (28)(12.6)\) = 224.4 square inches
Cost of this cereal box = 224.2×0.05 = $11.22
For the third box:
Volume = πr²h
r = 2.5 in and h = 12 in
Volume = π(2.5)²(12) = 235.61 cubic inches
Surface area = 2πr(h+r) = 2π(2.5)(12+2.5) = 227.76 square inches
Cost of this cereal box = 227.76×0.05 = $11.38
Thus, for the first box the volume, surface area, and cost of materials are 180 cubic inches, 258 square inches, and $12.9, for the second box 192 cubic inches, 224.4 square inches, and $11.22 for the third box 235.61 cubic inches, 227.76 square inches, and $11.38.
Learn more about the volume here:
https://brainly.com/question/16788902
#SPJ2
help with both please :)

Answers
Answer: I know two methods of solving both of the sums. One is the method of elimination, the other is method of substitution. You can do any of the given methods which is easier for you. Both methods will be shown below:
Method of Elimination1) 5x + y = 9 - - - - (i)
10x - 7y = - 18 - - - - (ii)
eq. (i) multiplied by 2
10x + 2y = 18 - - - - (i)
10x - 7y = - 18 - - - - (ii) {subtraction of eq. (ii) from eq. (i)}
0 + 9y = 36
y = 36/9
y = 4
From eq. (i),
5x + y = 9
-> 5x + 4 = 9
-> 5x = 9 - 4
-> x = 5/5
-> x = 1
So, x = 1 and y = 4
2) - 4x + 9y = 9 - - - - (i)
x - 3y = - 6 - - - - (ii)
eq. (ii) multiplied by 3
- 4x + 9y = 9 - - - - (i)
3x - 9y = - 18 - - (ii) {addition of eq. (ii) and eq. (i)}
- x + 0 = - 9
x = 9
From eq. (ii),
x - 3y = - 6
-> 9 - 3y = - 6
-> - 3y = -6-9
-> y = -15/-3
-> y = 5
So, x = 9 and y = 5
Method of Substitution1) 5x + y = 9 - - - - (i)
10x - 7y = - 18 - - - - (ii)
eq. (i)
5x + y = 9
-> y = 9 - 5x
Value of eq. (i) in eq. (ii)
10x - 7y = - 18
-> 10x - 7(9 - 5x) = - 18
-> 10x - 63 + 35x = - 18
-> 45x = - 18 + 63
-> x = 45/45
-> x = 1
From eq. (i),
5x + y = 9
-> 5 + y = 9
-> y = 9 - 5
-> y = 4
So, x = 1 and y = 4
2) - 4x + 9y = 9 - - - - (i)
x - 3y = - 6 - - - - (ii)
eq. (i)
- 4x + 9y = 9
-> - 4x = 9 - 9y
-> x = (9 - 9y) / -4
Value of eq. (i) in eq. (ii)
x - 3y = - 6
-> (9 - 9y) / -4 -3y = - 6
-> (9 - 9y + 12y) = - 6 * - 4
-> 3y = 24 - 9
-> y = 15/3
-> y = 5
From eq. (ii)
x - 3y = - 6
-> x - 3(5) = - 6
-> x - 15 = - 6
-> x = - 6 + 15
-> x = 9
So, x = 9 and y = 5
∩_∩
(„• ֊ •„)♡
┏━∪∪━━━━┓
hope it helped
┗━━━━━━━┛
Find all missing angles
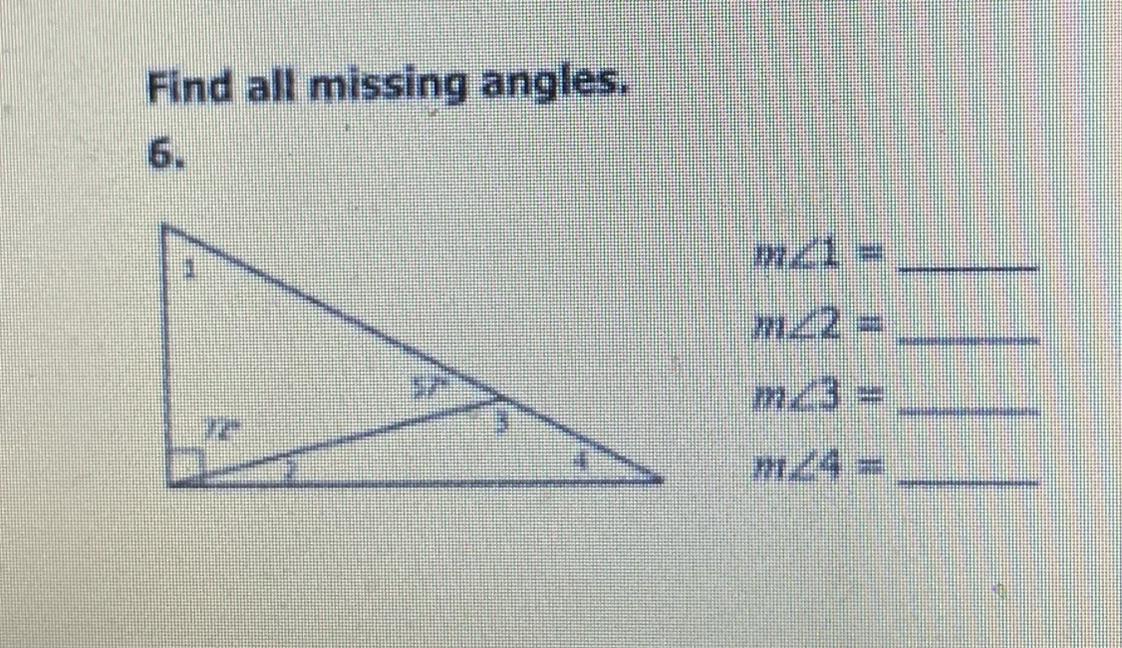
Answers
Answer:
1 = 51
2=18
3=123
4=39
Step-by-step explanation:
If M = {Prime integers between 1 and 11} and N = { factors of 12}. Find:
The members of M
The members of N
M∪N;
M∩N.
Please show working
Answers
Answer:
Step-by-step explanation:
M = {Prime integers between 1 and 11} and N = { factors of 12}. Find:
The members of M
The members of N
M∪N; M = {Prime integers between 1 and 11} and N = { factors of 12}. Find:
The members of M
The members of N
M∪N; M = {Prime integers between 1 and 11} and N = { factors of 12}. Find:
The members of M
The members of N
M∪N; M = {Prime integers between 1 and 11} and N = { factors of 12}. Find:
The members of M
The members of N
M∪N; M = {Prime integers between 1 and 11} and N = { factors of 12}. Find:
The members of M
The members of N
M∪N;
Answer:
M∪N = {1, 2, 3, 4, 5, 6, 7, 11, 12}M∩N = {2, 3}Step-by-step explanation:
GivenM = {Prime integers between 1 and 11} and N = { factors of 12}To findM∪N M∩NSolutionSets in full are
Prime numbers up to 11 ⇒ M = {2, 3, 5, 7, 11}Factors of 12 ⇒ N = {1, 2, 3, 4, 6, 12}Combined set
M∪N = {1, 2, 3, 4, 5, 6, 7, 11, 12}Common set
M∩N = {2, 3}______ has at least one solution, and an inconsistent system has no solution.
Answers
The statement "Consistent system of equations has at least one solution, and an inconsistent system has no solution" is true.
In the context of systems of linear equations, a consistent system refers to a system where there exists at least one solution that satisfies all the equations in the system. This means that the equations can be simultaneously satisfied by a set of values for the variables.
On the other hand, an inconsistent system refers to a system of equations that has no solution. This occurs when the equations are contradictory or cannot be satisfied simultaneously by any values for the variables.
Therefore, a consistent system guarantees the existence of at least one solution, while an inconsistent system does not have any solution.
To know more about Consistent system refer here:
https://brainly.com/question/12791933
#SPJ11
Use the definition of Taylor series to find the Taylor series (centered at c ) for the function. f(x)=e 4x
,c=0 f(x)=∑ n=0
[infinity]
Answers
The answer is , the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
The Taylor series expansion is a way to represent a function as an infinite sum of terms that depend on the function's derivatives.
The Taylor series of a function f(x) centered at c is given by the formula:
\(\large f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!}(x-c)^n\)
Using the definition of Taylor series to find the Taylor series (centered at c=0) for the function f(x) = e^(4x), we have:
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{e^{4(0)}}{n!}(x-0)^n\)
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n\)
Therefore, the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
To know more about Function visit:
https://brainly.in/question/222093
#SPJ11
The Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To find the Taylor series for the function f(x) = e^(4x) centered at c = 0, we can use the definition of the Taylor series. The general formula for the Taylor series expansion of a function f(x) centered at c is given by:
f(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)^2/2! + f'''(c)(x - c)^3/3! + ...
First, let's find the derivatives of f(x) = e^(4x):
f'(x) = d/dx(e^(4x)) = 4e^(4x)
f''(x) = d^2/dx^2(e^(4x)) = 16e^(4x)
f'''(x) = d^3/dx^3(e^(4x)) = 64e^(4x)
Now, let's evaluate these derivatives at x = c = 0:
f(0) = e^(4*0) = e^0 = 1
f'(0) = 4e^(4*0) = 4e^0 = 4
f''(0) = 16e^(4*0) = 16e^0 = 16
f'''(0) = 64e^(4*0) = 64e^0 = 64
Now we can write the Taylor series expansion:
f(x) = f(0) + f'(0)(x - 0) + f''(0)(x - 0)^2/2! + f'''(0)(x - 0)^3/3! + ...
Substituting the values we found:
f(x) = 1 + 4x + 16x^2/2! + 64x^3/3! + ...
Simplifying the terms:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
Therefore, the Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To know more about Taylor series, visit:
https://brainly.com/question/32235538
#SPJ11
What is the solution to the system of equations?

Answers
Answer:
(1, 3 )
Step-by-step explanation:
The solution is at the point of intersection of the 2 lines
The lines intersect at (1, 3 ) , then
solution is (1, 3 )
jadas turtle walked 10 feet then half that length
Answers
Answer:
he walked 15 feet in total
Step-by-step explanation:
I'm not sure if u asked a question or not