The art club is designing a rectangular mural for the school hallway. Three
corners are located at (21,21),(21, 1), and (4.1) on a coordinate plane. Find the
fourth vertex and graph the rectangle on the coordinate plane below.
Fourth vertex:
Answers
The 4th vertex of the rectangle is given by D ( 4 , -1 ) and the graph is plotted
What is the area of a rectangle?The product of the rectangle's length and its breadth determines the area of the rectangle.
Rectangle area equals length times width
Given data ,
Let the area of the rectangle be represented as S
Let the rectangle be represented as ABCD
The coordinates of A = A ( -1 , -1 )
The coordinates of B + B ( -1 , 1 )
The coordinates of C = C ( 4 , 1 )
So , the length of the rectangle = 4 units
The width of the rectangle = 2 units
So , the area of the rectangle S = 4 x 2 = 8 units
And , the 4th vertex of rectangle D = D ( 4 , -1 )
Hence , the coordinate D of rectangle is D ( 4, -1 )
Read more about rectangles here:
https://brainly.com/question/25292087
#SPJ1

Related Questions
The city has a section of land, 3,694.7 ft long. The city wants to make 100 equal-sized gardens with this land. How long will each garden be?
Answers
Answer:
Give me a heart and 5 stars
Step-by-step explanation:

Answer:
This is straightforward. To find how long each garden plot would be, we only need to divide. So to obtain 10 equal-sized garden plots from a 3694.7 feet land we have 3694.7/ 10 = 369.47 ft.
THERE MARK ME BRINILYLIST
Consider the graphed function.
YA
8
O
-6
-4
-2.
-8
-6
-4
-2
2
4
6
8
2
3
4
-6
-8
What are the domain and the range of this function?

Answers
Answer:
-5, -4
Step-by-step explanation:
blah oiwhfnwpiem qipewd
The domain and range of the graphed function
Domain; -5 ≤ x < 1
Range; -4 ≤ y < 7
What is Domain and Range of function?Simply expressed, the domain is the collection of all potential input values. This means the values on the graph's x-axis. Meanwhile, the range is the collection of all output values, which in this case are the y-axis values.
Now, from the graph, we see that the line stopped at 2 points.
The bottom one is darkened, indicating that it contains the numbers at that point.
So, the domain as x ≥ -5
While the range will be as follows; y ≥ -5
The location where it is not coloured on the graph for the second point above indicates that the coordinates at that point are not included in the range or domain.
Hence, the domain here is; x < 1
and, y < 7 is the range.
Now, combining the Domain and Range as
Domain = -5 ≤ x < 1
Range; -4 ≤ y < 7
Learn more about Domain and Range here: brainly.com/question/19819428
#SPJ7
In the year 2004, a survey was undertaken to find whether citizens of a certain political party supported their party's candidate for governor. In a sample of 300 citizens of this party, 95% of them expressed support for their party's candidate. A similar survey was conducted four years later and showed that 91% of a sample of 350 citizens of this party expressed support for their party's candidate. Construct a 95% confidence interval for the difference in population proportions of citizens of this party who supported their gubernatorial candidate in 2004 and citizens of this party who supported their gubernatorial candidate four years later. Assume that random samples are obtained and the samples are independent. (Round your answers to three decimal places.) z0.10 z0.05 z0.025 z0.01 z0.005 1.282 1.645 1.960 2.326 2.576
Answers
Answer:
The 95% confidence interval for the difference in population proportions is (0.001, 0.079).
Step-by-step explanation:
The (1 - α)% confidence interval for the difference in population proportions is:
\(CI=(\hat p_{1}-\hat p_{2})\pm z_{\alpha /2}\times\sqrt{\frac{\hat p_{1}(1-\hat p_{1})}{n_{1}}+\frac{\hat p_{2}(1-\hat p_{2})}{n_{2}}}\)
The information provided is as follows:
\(\hat p_{1}=0.95\\\hat p_{2}=0.91\\n_{1}=300\\n_{2}=350\\\)
The critical value of z for 95% confidence level is 1.96.
Compute the 95% confidence interval for the difference in population proportions as follows:
\(CI=(\hat p_{1}-\hat p_{2})\pm z_{\alpha /2}\times\sqrt{\frac{\hat p_{1}(1-\hat p_{1})}{n_{1}}+\frac{\hat p_{2}(1-\hat p_{2})}{n_{2}}}\)
\(=(0.95-0.91)\pm 1.96\times\sqrt{\frac{0.95(1-0.95)}{300}+\frac{0.91(1-0.91)}{350}}\\\\=0.04\pm 0.0388\\\\=(0.0012, 0.0788)\\\\\approx (0.001, 0.079)\)
Thus, the 95% confidence interval for the difference in population proportions is (0.001, 0.079).
Find constants a and b such that the function y = a sin(x) + b cos(x) satisfies the differential equation y'' + y' − 5y = sin(x).
Answers
Answers:
a = -6/37
b = -1/37
============================================================
Explanation:
Let's start things off by computing the derivatives we'll need
\(y = a\sin(x) + b\cos(x)\\\\y' = a\cos(x) - b\sin(x)\\\\y'' = -a\sin(x) - b\cos(x)\\\\\)
Apply substitution to get
\(y'' + y' - 5y = \sin(x)\\\\\left(-a\sin(x) - b\cos(x)\right) + \left(a\cos(x) - b\sin(x)\right) - 5\left(a\sin(x) + b\cos(x)\right) = \sin(x)\\\\-a\sin(x) - b\cos(x) + a\cos(x) - b\sin(x) - 5a\sin(x) - 5b\cos(x) = \sin(x)\\\\\left(-a\sin(x) - b\sin(x) - 5a\sin(x)\right) + \left(- b\cos(x) + a\cos(x) - 5b\cos(x)\right) = \sin(x)\\\\\left(-a - b - 5a\right)\sin(x) + \left(- b + a - 5b\right)\cos(x) = \sin(x)\\\\\left(-6a - b\right)\sin(x) + \left(a - 6b\right)\cos(x) = \sin(x)\\\\\)
I've factored things in such a way that we have something in the form Msin(x) + Ncos(x), where M and N are coefficients based on the constants a,b.
The right hand side is simply sin(x). So we want that cos(x) term to go away. To do so, we need the coefficient (a-6b) in front of that cosine to be zero
a-6b = 0
a = 6b
At the same time, we want the (-6a-b)sin(x) term to have its coefficient be 1. That way we simplify the left hand side to sin(x)
-6a -b = 1
-6(6b) - b = 1 .... plug in a = 6b
-36b - b = 1
-37b = 1
b = -1/37
Use this to find 'a'
a = 6b
a = 6(-1/37)
a = -6/37
describe a family member in 3-5 sentences (use nouns) make it easy and simple please!!
Answers
p(5)=
p(1 or 2)=
p(odd number)=
p(not 6)=
p(even number)=
p(1,2,3,or 4)=
Answers
The probabilities, we need to understand the context. Assuming we are working with a fair six-sided die, where each face has an equal chance of landing, here are the probabilities:
P(5): Since there is only one face with a value of 5 on the die, the probability of rolling a 5 is 1/6.P(1 or 2): There are two faces with the values 1 and 2 respectively. Since these are mutually exclusive events (you can only roll one of them at a time), the probability of rolling a 1 or a 2 is 2/6, which simplifies to 1/3.P(odd number): Out of the six faces, three are odd numbers (1, 3, and 5). So, the probability of rolling an odd number is 3/6, which simplifies to 1/2.P(not 6): Since there is only one face with a value of 6, the probability of not rolling a 6 is 5/6.P(even number): Out of the six faces, three are even numbers (2, 4, and 6). So, the probability of rolling an even number is 3/6, which simplifies to 1/2.P(1, 2, 3, or 4): There are four faces with the values 1, 2, 3, and 4. Therefore, the probability of rolling any of these numbers is 4/6, which simplifies to 2/3.For such more questions on probability
https://brainly.com/question/30390037
#SPJ8
What is AC? Giving brainliest

Answers
AC ^2 = 36
AC = 6
a high school sells students tickets for $5 as well as general admission tickets for $7 to attend thier football games. The school needs to bring in at least $1500 per game in order to maintain the costs of the football team
Answers
The cost of students ticket is $37.5and the cost of general admission is $187.5.
What is system of equations?A finite set of equations for which common solutions are sought is referred to in mathematics as a set of simultaneous equations, also known as a system of equations or an equation system.
Assume s be the students tickets cost and g be the general admission cost.
From the given information,
⇒ s + g = 225 ..(1)
5s + 7g = 1500 ..(2)
From equation (1),
s = 225 - g
Plug the value of s in equation (2)
5(225 - g) + 7g = 1500
1125 - 5g + 7g = 1500
2g = 1500 - 1125
2g = 375
g = 187.5
Plug g = 125 in equation (1),
s + 187.5= 225
s = 225 - 187.5
s = 37.5
To know more about system of equations, click on the link
brainly.com/question/13729904
#SPJ1
Question content area top
Part 1
Read the clues about the current ages of some of the members of the Ruiz family. Ben is one year younger than Amara. Amara is 18 years old, Maria is 5 years old, and Tony is 2 years old. Write an equation that can be used to find Isabelle's age, i. How old is Isabelle?
Answers
So Isabelle is 18 times old.
Ben is one time youngish than Amara, so Ben's age is 18- 1 = 17.
Maria is 5 times old, and Tony is 2 times old.
Let's use" i" to represent Isabelle's age. also, we can set up the equation
5 2 i = total family age
We can simplify this equation to
24 i = total family age
To find Isabelle's age, we need to know the total family age. We can calculate this by adding up the periods of all the family members
18 17 5 2 i = 42 i
Now we can substitute this expression for the total family age back into our equation
24 i = 42 i
Simplifying this equation, we get
i = 18
To further about the equation visit : https://brainly.com/question/2416975
#SPJ1
How many triangles can be drawn with the side lengths of 3 units, 4 units, and 5 units? Explain.
Answers
The number of triangles that can be drawn from the given side lengths is; 1 perfect right angle triangle
Right angle triangle proof
We are given the sides of the triangle to be;
3 units, 4 units and 5 units
Now, let us test if it is a right angled triangle by using the Pythagoras theorem as follows where;
a² + b² = c²
let a and b be 3 and 4 respectively. Thus;
3² + 4² = 16 + 9 = 25
c is 5. Thus; 5² = 25
Thus, we see that the 3 given sides fulfill the conditions of a right angle triangle.
Read more about right angle triangle at; https://brainly.com/question/1248322
what is the area of the figure?

Answers
Answer:I’m guessing the second one
Step-by-step explanation:
I thinking that because if u add it all up also this is just a thought
What is the solution to x2 – 9x < –18? ASAP will give brainliest
x < –6 or x > 3
–6 < x < 3
x < 3 or x > 6
3 < x < 6
Answers
The solution to the inequality equation \(x^{2}\) – 9x < –18 is 3 < X < 6
Inequality equationInequality equation means a mathematical expression in which the sides are not equal to each other
\(x^{2}\) – 9x < –18
Rewrite in standard form
x^2 -9x +18 < 0
Factorise the equation
\(x^{2}\) - 3x -6x +18 < 0
x (x - 3) - 6 (x - 3) < 0
(x - 3) ( x- 6) < 0
(x - 3) < 0
x < 3
( x- 6) < 0
x < 6
3 < X < 6
Therefore, the solution to the inequality is 3 < X < 6
Learn more about inequality equation here: https://brainly.com/question/24372553
#SPJ1
Is 2x - 3 = -7 x + 2 > y a true or false statement?
Answers
what is the area of a rectangles with the side lengths 5 inches and 4/3 inches?
Answers
Answer: 20/3 square inches
Step-by-step explanation:
Area = length*width
length = 5 in.
width = 4/3 in.
A = 5 * (4/3) = 20/3 in^2
Read the following two statements. Then, if possible, use the Law of Detachment to draw a conclusion. The doctor recommends rest if the patient has the flu. The doctor recommends rest. not possible The patient does not have the flu. If the doctor recommends rest, the patient has the flu. The patient has the flu.
Answers
The doctor recommends rest if the patient has the flu. Then the correct option is A.
What is decision-making?Determining the proper option, acquiring evidence, and exploring various options are all steps in the decision-making process.
Read the following two statements.
Then, if possible, use the Law of Detachment to draw a conclusion.
Then the correct option is A.
The doctor recommends rest if the patient has the flu.
More about the decision-making link is given below.
https://brainly.com/question/3369578
#SPJ1
Hello can someone please answer this question i will mark you the Brainliest

Answers
Answer:
A) 310 cm²
Step-by-step explanation:
The surface area is the area of the two-dimensional surfaces of this three-dimensional figure.
Start by multiplying each 5x4 rectangle. There are four of them that are visible from the front.
4(5 · 4) 4(20) = 80 cm²Now, find the surface area of the large rectangle in the back and the left side of the figure.
2(10 · 4) = 80 cm²Find the surface area of the top of this figure.
10 · 5 = 50 cm²5 · 5 = 25 cm²Find the surface area of the bottom of this figure (it's the same as the area of the top).
50 + 25 = 75 cm²Add all of the surface areas together to find the total surface area of the figure.
80 + 80 + 75 + 75 = 310 cm²Using this linear inequality: 10C + 4 > 2C
Explain how to solve the inequality use both English and Math Sentences in your explanation, and how complete your explanation is.
Answers
Answer:
C > –½
Step-by-step explanation:
10C + 4 > 2C
The above inequality can be solved as follow:
10C + 4 > 2C
Collect like terms
4 > 2C – 10C
4 > – 8C
Divide both side by –8
Note: the inequality sign will change since we are dividing by a negative value.
4/ –8 < –8C/ –8
– ½ < C
Thus,
C > –½
A line has a slope of -4. The line passes through the point (-2,1). What is the point- slope form of the line?
y - 1 = -4 (x + 2)
y - 4 = -2 (x - 1)
y - 1 = 4 (x - 2)
y - 2 = -4 (x - 1)
Answers
Answer:
the answer is A
I followed the point slope formula and added in the x and y values

solve this proportion: 5/a = 3/4
Answers
Answer:
\(a = \frac{20}{3}\)
Step-by-step explanation:
what is the value of 3.85+0.004+0.117?
Answers
Answer: 3.971
Step-by-step explanation: first, you need to set up your addition problem. When adding decimals, you need to line up the decimal points. So you get something like this:
3.85
0.004
0.117
+————-
Then you add vertically and you get your answer of 3.971
Your welcome :)
The value of the given expression ( 3.85+0.004+0.117 ) is 3.971.
What is summation?
The process of increment of any number of quantities or the process of integrating small parts to make a big part is called summation.
first, you need to set up your addition problem. When adding decimals, you need to line up the decimal points. So you get something like this:
3.850
0.004
0.117
+————-
3.971.
Then you add vertically and you get your answer of 3.971.
To know more about summation follow
brainly.com/question/542712
#SPJ2
Can someone answer with steps and explanation? Thanks.

Answers
Answer:\(\color{yellow}{}\)
∆ABC
∆DEF
∆ABC
<C
<D
<X
BE>
CF>
AD>
34>
x9×>
A=3.7
The measure of an angle is 139.2°. What is the measure of its supplementary angle?
Answers
Supplementary angles mean two angles that add up to 180.
180 = 139.2 (angle 1) + x (angle 2)
180 - 139.2 = x (angle 2)
40.8 = x
angle 2 = 40.8
Answer:
40.8°
Step-by-step explanation:
The sum of two supplementary angles is 180°.
180 - 139.2 = 40.8
The measure of it's supplement should be 40.8°.
Hope this helps.
Ann 's car can go 132 miles on 4 gallons of gas. During a drive last weekend, Ann used 5 gallons of gas. How far did she drive? Use pencil and paper. Explain how the problem changes if you were given the distance Ann drove last weekend instead of how much gas she used.
Answers
Answer:
Ann traveled 165 miles on 5 gallons of gas
Step-by-step explanation:
First we must know how many miles are in a gallon (in this situation). Last weekend Ann drove 132 miles with 4 gallons of gas, we can divide to find out how many miles she drove on 1 gallon. 132/4 = 33. This means Ann drove 33 miles on 1 gallon of gas. To get your answer, simply multiply 5 and 33. 5 times 33 = 165.
A 78.0 kg sprinter starts a race with an acceleration of 1.64 m/s2. If the sprinter accelerates at that rate for 25 m, and then maintains that velocity for the remainder of the 100 m dash, what will be his time (in s) for the race?
Answers
The sprinter will complete the race in approximately 17.07 seconds.
To calculate the time for the race, we need to consider two parts: the acceleration phase and the constant velocity phase.
Acceleration Phase:
The acceleration of the sprinter is 1.64 m/s², and the distance covered during this phase is 25 m. We can use the equation of motion to calculate the time taken during acceleration:
v = u + at
Here:
v = final velocity (which is the velocity at the end of the acceleration phase)
u = initial velocity (which is 0 since the sprinter starts from rest)
a = acceleration
t = time
Rearranging the equation, we have:
t = (v - u) / a
Since the sprinter starts from rest, the initial velocity (u) is 0. Therefore:
t = v / a
Plugging in the values, we get:
t = 25 m / 1.64 m/s²
Constant Velocity Phase:
Once the sprinter reaches the end of the acceleration phase, the velocity remains constant. The remaining distance to be covered is 100 m - 25 m = 75 m. We can calculate the time taken during this phase using the formula:
t = d / v
Here:
d = distance
v = velocity
Plugging in the values, we get:
t = 75 m / (v)
Since the velocity remains constant, we can use the final velocity from the acceleration phase.
Now, let's calculate the time for each phase and sum them up to get the total race time:
Acceleration Phase:
t1 = 25 m / 1.64 m/s²
Constant Velocity Phase:
t2 = 75 m / v
Total race time:
Total time = t1 + t2
Let's calculate the values:
t1 = 25 m / 1.64 m/s² = 15.24 s (rounded to two decimal places)
Now, we need to calculate the final velocity (v) at the end of the acceleration phase. We can use the formula:
v = u + at
Here:
u = initial velocity (0 m/s)
a = acceleration (1.64 m/s²)
t = time (25 m)
Plugging in the values, we get:
v = 0 m/s + (1.64 m/s²)(25 m) = 41 m/s
Now, let's calculate the time for the constant velocity phase:
t2 = 75 m / 41 m/s ≈ 1.83 s (rounded to two decimal places)
Finally, let's calculate the total race time:
Total time = t1 + t2 = 15.24 s + 1.83 s ≈ 17.07 s (rounded to two decimal places)
Therefore, the sprinter will complete the race in approximately 17.07 seconds.
For such more questions on Sprinter Race Time Calculation
https://brainly.com/question/18963548
#SPJ8
Function or Not a Function
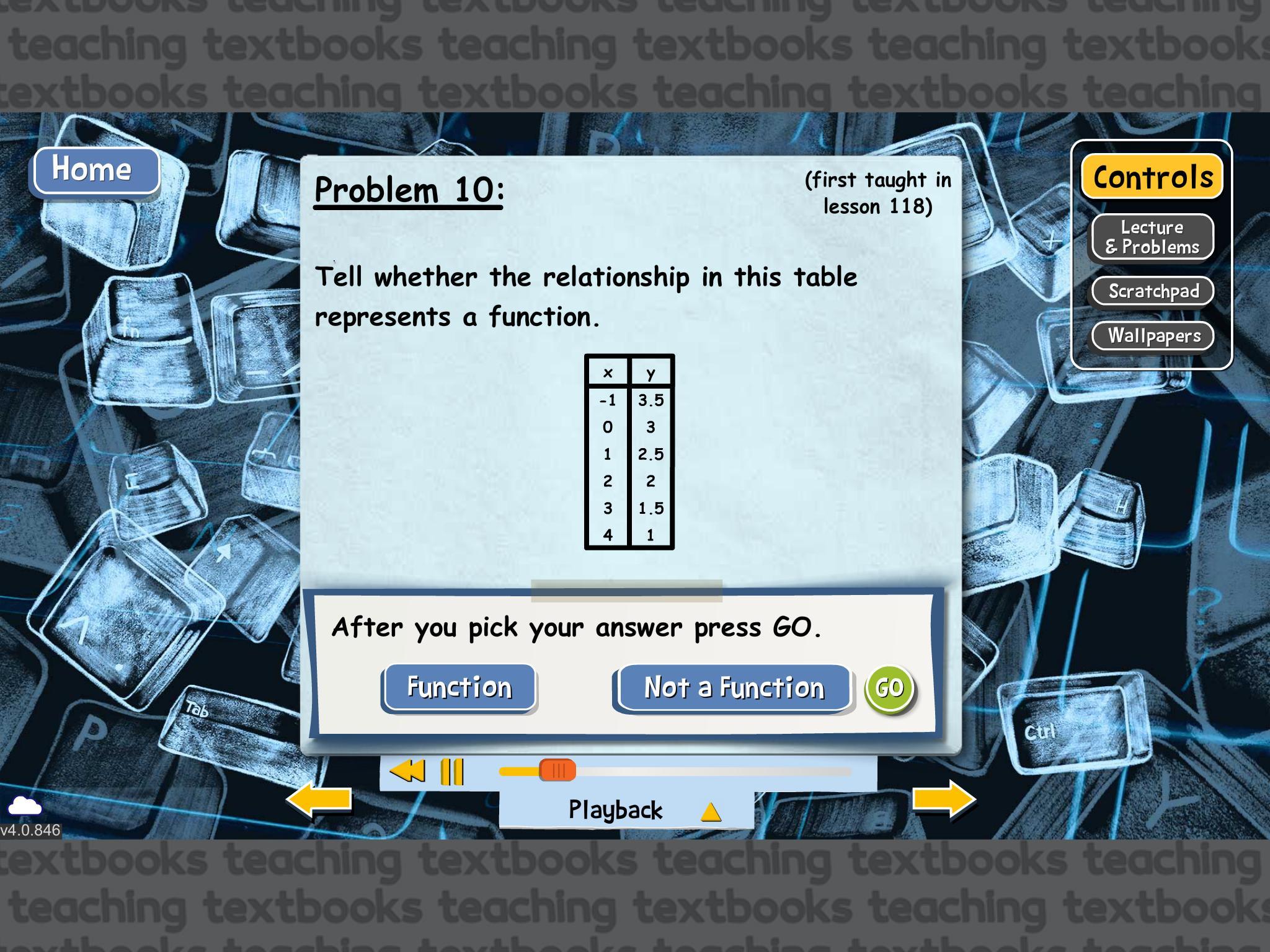

Answers
Step-by-step explanation:
problem 10 is function
but problem 9 is not
Please help me in this math problem

Answers
Answer:
Step-by-step explanation: well, you will more than likely get it at least 60%-80% of the time! If this doesn't help i can try to explain in a lot more detail unless someone does for me!
The number of failures of a testing instrument from contamination particles on the product is a Poisson random variable with a mean of 0.025 failure per hour.(a) What is the probability that the instrument does not fail in an 8-hour shift?(b) What is the probability of at least one failure in a 24-hour day?Round your answers to four decimal places (e.g. 98.7654).
Answers
(a) The probability that the instrument does not fail in an 8-hour shift is 0.7183 or 71.83%.
(b) The probability of at least one failure in a 24-hour day is 0.999 or 99.9%.
Poisson Distribution: Failure ProbabilityThe number of failures of a testing instrument in a given time period is modeled by a Poisson distribution with a rate parameter equal to the mean number of failures per unit time.
(a) To find the probability that the instrument does not fail in an 8-hour shift, we can use the cumulative distribution function (CDF) of the Poisson distribution. The CDF gives the probability that the number of failures is less than or equal to a given value. In this case, we want to find the probability that there are 0 failures in an 8-hour shift, so the CDF can be expressed as:
P(X ≤ 0) = e^(-0.025 * 8) = 0.7183
So, the probability that the instrument does not fail in an 8-hour shift is 0.7183 or 71.83%.
(b) To find the probability of at least one failure in a 24-hour day, we can subtract the probability of 0 failures from 1. That is,
P(X ≥ 1) = 1 - P(X ≤ 0) = 1 - e^(-0.025 * 24) = 0.999
So, the probability of at least one failure in a 24-hour day is 0.999 or 99.9%.
Note: In these calculations, we use the formula for the cumulative distribution function of the Poisson distribution, which is:
P(X ≤ k) = e^(-lambda) * (lambda^k / k!)
Learn more about Poisson Distribution: Failure Probability here:
https://brainly.com/question/29564533
#SPJ4
Krista designs quilts using the pattern shown. The table of values describes the shaded area of the pattern in square units, y, as a function of the length of a side,X units. Which equation describes this relationship?

Answers
The equation which describes the relationship between the side length and shaded area of the quilt is y=0.5x²
Modeling relationship between two variablesSide length, x = 1,3,4,5,8
Shaded Area, y = 0.5, 4.5, 8, 12.5, 32
The relationship can be modeled as a quadratic function. Using a graphing calculator for the quadratic function written in the form y = ax² + bx + c
a = 0.5 ; b = 0 ; c = 0
Therefore, the quadratic function can be written as y = 0.5x²
Learn more on quadratic functions ; https://brainly.com/question/1214333
#SPJ1

What is the relationship among angle BCD and angle A, and angle B in the figure below?
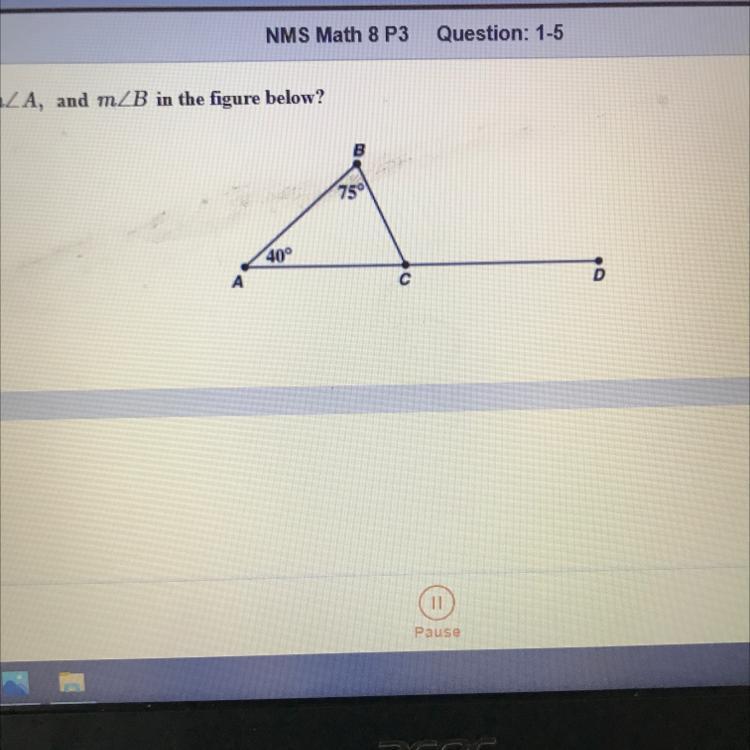
Answers
Answer:
relationship
the exterior angle of triangle is equal to the sum of its opposite angle
<A+<B=<BÇD
Kelly is making a bubble mixture for kids to play with at a backyard party. She adds 1/4 of a cup of corn syrup to 6 cups of soap and water.
She wants to make more bubble mixture and has 18 cups of the soap and water mixture to use.
How much corn syrup does she need to add?
A. 2/3 of a cup of corn syrup
B. 3 cups of corn syrup
C. 3/4 of a cup of corn syrup
D. 3 1/4 cups of corn syrup
Answers
Answer: C. 3/4 of a cup of corn syrup
Step-by-step explanation:
We will set up a proportion to help us solve.
\(\displaystyle \frac{1/4\text{ cup corn syrup}}{6\text{ cups of soap and water}} =\frac{x\text{ cups corn syrup}}{18\text{ cups of soap and water}}\)
Next, we will cross-multiply.
1/4 * 18 = 6 * x
9/2 = 6x
Lastly, we will divide both sides of the equation by 6.
x = 3/4 of a cup of corn syrup
C. 3/4 of a cup of corn syrup