The intensity of sound is measured on the decibel scale, dB. The equation
dB 10 log I represents the decibel level, where I is the ratio of the sound to
the human hearing threshold. A noise registers a decibel level of 29. What is the
value of I? Round to the nearest whole number.
A) 42071
B) 18
C) 89
D) 794
Answers
Answer: D) 794
Step-by-step explanation:
\(10lgI=29\)
Divide both parts of the equation by 10:
\(lgI=2.9\\\\I=10^{2.9}\\\\I\approx794\)
Related Questions
determine slope and y-intercept
Use the following table to answer questions #19 and #20.

Answers
Answer:
Slope. -6
Y- intercept. 180
Perform each operation.
(x^2-6x+9)-2(x^2-3x+1)
Answers
Answer:
\(\huge\boxed{(x^2-6x+9)-2(x^2-3x+1)=-x^2+7}\)
Step-by-step explanation:
\((x^2-6x+9)-2(x^2-3x+1)\qquad|\text{use the distributive property}\\\\=x^2-6x+9+(-2)(x^2)+(-2)(-3x)+(-2)(1)\\\\=x^2-6x+9-2x^2+6x-2\qquad|\text{combine like terms}\\\\=(x^2-2x^2)+(-6x+6x)+(9-2)\\\\=-x^2+7\)
hope this helps
Function A and Function B are linear Functions. Function A is represented by the equation
y= -2x+w. Function B is represented by the graph. Which statement is true?
A. The slope of function A is the same as the slope of Function B.
B. The slope of Function A is negative and the slope of Function B is positive.
C. The slope of Function A and B are both positive.
D. The slope of Function A and B are both negative.
Function B
Function A
y = -2x+3
1
2
7
Your answer
Answers
Answer:
6.0 and the other things that you want me on my way 6.0 and if I can
Answer:
I think it is 6.0
Step-by-step explanation:
Hope this helped have an amazing day/month/year!
can someone help me please i don't understand this

Answers
The transformation that would not result in a congruent figure when performed on triangle RST is A. A dilation by a scale factor of 2 with respect to point R.
The equation that has the same solution as the system of equations is C. 4x + 9y = 10
4x + 6y = 24.
Which transformations changes congruency ?Transformations that change the shape or size of a figure can change its congruency. A dilation is a transformation that changes the size of a figure so this would mean that RST dilated would not result in a congruent figure.
How to find the equation?When the system of equations, 4x + 9y = 10, 2x + 3y = 12 is solved, we find that x = 13 and y = - 14/ 3.
Options A,B, and D cannot have the same value because the numbers are the same and so they should have different values., Only option C can be the same and when the values are slotted in, this is proven.
Option C, 4x + 9y = 10 , 4x + 6y = 24 is therefore correct.
Find out more on equations at https://brainly.com/question/25869125
#SPJ1
use the laplace transform to solve the given initial-value problem. y' 5y = f(t), y(0) = 0, where f(t) = t, 0 ≤ t < 1 0, t ≥ 1
Answers
The solution to the initial-value problem using the Laplace transform is y(t) = (1/25)(1 - \(e^{(-5t)\)) - (1/25)t + (1/125)\(e^{(-5t)\).
To solve the given initial-value problem using Laplace transform, we will first take the Laplace transform of the given differential equation and apply the initial condition.
Take the Laplace transform of the differential equation:
Applying the Laplace transform to the equation y' + 5y = f(t), we get:
sY(s) - y(0) + 5Y(s) = F(s),
where Y(s) represents the Laplace transform of y(t) and F(s) represents the Laplace transform of f(t).
Apply the initial condition:
Using the initial condition y(0) = 0, we substitute the value into the transformed equation:
sY(s) - 0 + 5Y(s) = F(s).
Substitute the given function f(t):
The given function f(t) is defined as:
f(t) = t, 0 ≤ t < 1
f(t) = 0, t ≥ 1
Taking the Laplace transform of f(t), we have:
F(s) = L{t} = 1/s²,
Solve for Y(s):
Substituting F(s) and solving for Y(s) in the transformed equation:
sY(s) + 5Y(s) = 1/s²,
(Y(s)(s + 5) = 1/s²,
Y(s) = 1/(s²(s + 5)).
Inverse Laplace transform:
To find y(t), we need to take the inverse Laplace transform of Y(s). Using partial fraction decomposition, we can write Y(s) as:
Y(s) = A/s + B/s² + C/(s + 5),
Multiplying both sides by s(s + 5), we have:
1 = A(s + 5) + Bs + Cs².
Expanding and comparing coefficients, we get:
A = 1/25, B = -1/25, C = 1/125.
Therefore, the inverse Laplace transform of Y(s) is:
y(t) = (1/25)(1 - \(e^{(-5t)\)) - (1/25)t + (1/125)\(e^{(-5t)\).
Learn more about laplace transform at
https://brainly.com/question/30759963
#SPJ4
-Question 6, 5.2.19Find the interest rate for a $9500 deposit accumulating to $11,346, compounded annually for 7 years.The interest rate is_____%.(Do not round until the final answer. Then round to two decimal places as needed.

Answers
GIVEN
A compound interest account with a principal of $9500 accumulating to $11346 in 7 years, compounded annually.
TO FIND
The interest rate.
SOLUTION
The compound interest formula is given to be:
\(A = P(1 + \frac{r}{n})^{nt}\)where
A = final amount
P = initial principal balance
r = interest rate
n = number of times interest applied per time period
t = number of time periods elapsed.
From the question, the following parameters are seen:
\(\begin{gathered} A=11346 \\ P=9500 \\ n=1\text{ \lparen annual compounding\rparen} \\ t=7 \end{gathered}\)Therefore:
\(\begin{gathered} 11346=9500(1+\frac{r}{1})^{1\times7} \\ 11346=9500(1+r)^7 \end{gathered}\)Solve for r:
\(\begin{gathered} (1+r)^7=\frac{11346}{9500} \\ 1+r=\sqrt[7]{\frac{11346}{9500}} \\ r=\sqrt[7]{\frac{11346}{9500}}-1 \\ r=0.02569 \end{gathered}\)Multiply by 100:
\(\begin{gathered} r=2.569\% \\ r\approx2.57\% \end{gathered}\)ANSWER
The interest rate required to get a total amount of $11,346.00 from compound interest on a principal of $9,500.00 compounded once per year over 7 years is 2.57% per year.
I need help ASAP!!!
Thx!!!

Answers
Answer:
c
Step-by-step explanation:
because i said so
Please help me,.........
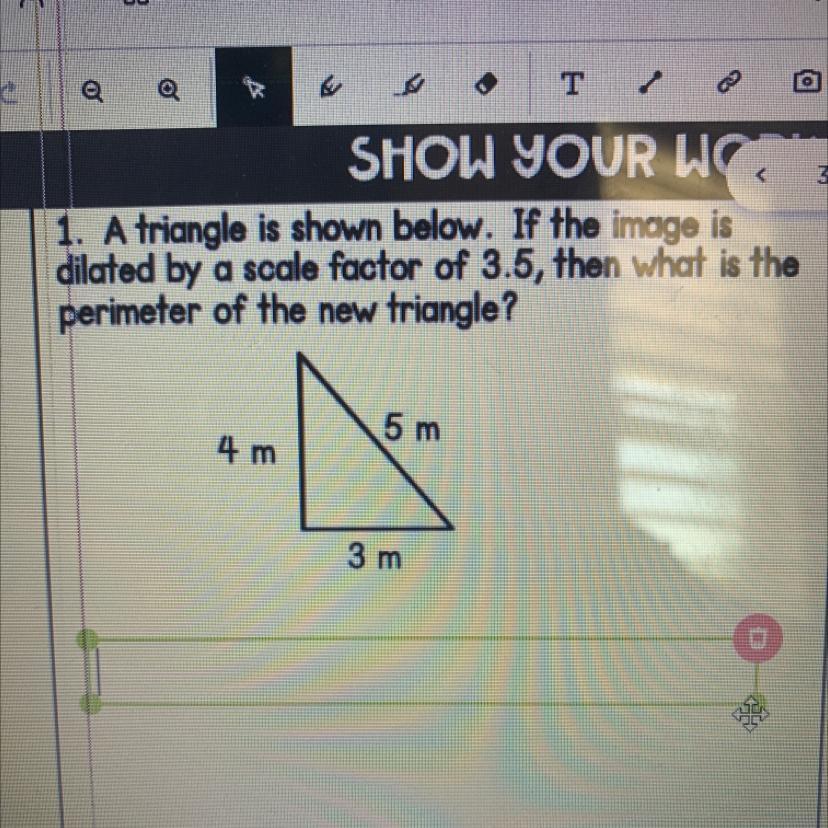
Answers
Answer
19?
Step-by-step explanation:
PLEASE HELP!!! I don't understand rate of change so please include a bit of an explaination. Use the table to find the rate of change

Answers
Answer:
4
Step-by-step explanation:
every 2 servings, 8 oz. every 1 serving, 4 oz.
Answer:
try looking up rise over run method. that's what i was taught to use for rate of change. it's easier so basically it's x over y
Step-by-step explanation:
10 problemas de ecuaciones de primer grado relacionada los datos con el cambio climático
Answers
Answer: Si la emisión de gases de efecto invernadero aumenta en un 5% anual, ¿cuánto aumentará la temperatura global en 20 años?
Solución: Dado que cada
Step-by-step explanation:
Una empresa produce 400 toneladas de dióxido de carbono al año. Si cada tonelada de dióxido de carbono contribuye al calentamiento global en 0.05 grados Celsius, ¿cuál será el aumento de temperatura causado por la empresa en un año?
Solución: 400 x 0.05 = 20 grados Celsius
La temperatura media de la Tierra ha aumentado en 1 grado Celsius desde la era preindustrial.
Si el aumento de temperatura está directamente relacionado con la cantidad de dióxido de carbono en la atmósfera, ¿cuánto dióxido de carbono adicional se ha emitido desde la era preindustrial hasta ahora?
Solución: Dado que cada tonelada de dióxido de carbono contribuye a un aumento de 0.05 grados Celsius, 1 / 0.05 = 20. Por lo tanto, se han emitido 20 veces la cantidad de dióxido de carbono necesario para contribuir a un aumento de 1 grado Celsius.
Una central térmica produce 1000 megavatios de electricidad al día. Si la eficiencia de conversión de la central térmica es del 30%, ¿cuántas toneladas de dióxido de carbono se emiten al día?
Solución: La eficiencia de conversión de la central térmica es del 30%, lo que significa que se pierde el 70% de la energía.
Por lo tanto, la cantidad de energía producida por la central térmica es de 1000 x 0.3 = 300 megavatios. Si cada megavatio produce 0.5 toneladas de dióxido de carbono, entonces la central térmica emite 300 x 0.5 = 150 toneladas de dióxido de carbono al día.
Si se reduce la emisión de dióxido de carbono en un 20%, ¿en qué medida se reducirá el aumento de temperatura global?
Solución: Si se reduce la emisión de dióxido de carbono en un 20%, se reducirá el aumento de temperatura global en un 20% x 0.05 = 0.01 grados Celsius.
Si la temperatura media en una ciudad ha aumentado en 0.5 grados Celsius en los últimos 10 años, ¿cuál es la tasa de aumento de temperatura por año?
Solución: La tasa de aumento de temperatura por año es de 0.5 grados Celsius / 10 años = 0.05 grados Celsius por año.
Si la concentración de dióxido de carbono en la atmósfera es de 400 partes por millón (ppm) y se espera que aumente en un 2% anual, ¿cuál será la concentración de dióxido de carbono en 10 años?
Solución: El aumento anual de la concentración de dióxido de carbono es de 400 x 0.02 = 8 ppm. Por lo tanto, la concentración de dióxido de carbono en 10 años será de 400 + 8 x 10 = 480 ppm.
Si la emisión de gases de efecto invernadero aumenta en un 5% anual, ¿cuánto aumentará la temperatura global en 20 años?
Solución: Dado que cada
To know more about invernadero refer here
https://brainly.com/question/25286039#
#SPJ11
Explain 2+2=5
how is it possible?
Answers
By having very large values of 2. Rounding 2.26 to the closest integer yields 2. 2.26+2.26 = 4.52, which, rounded to nearest integer, makes 5. So 2+2 = 5, with very large values of 2.
Compare the two integers below:
11____-1
<
>
=

Answers
Answer:
B. >
Step-by-step explanation:
Yes, you got it correct! Anything with a "-" is always less than a "+". Look at it this way:
I have 11 dollars (+11) and you owe me one dollar (-1). Now which is better?
Hope this helps
~R3VO
Blueprint
3 in
Deck
3 in
1 in
1 in
1 In
The area of the scale drawing is
square inches.
If the scale is 1 inch = 4 feet, the area of the actual deck would be
Numerically, the value of the area of the actual deck would be
Based on these results, if the scale is 1 inch = k feet, the area of the actual deck would be "
square feet.
times the value of the area of the scale drawing.
square feet

Answers
Area of the scale drawing is 10 square inches. Area of the actual deck would be 160 square feet.
Area of the actual deck would be 16 times the area of the scale drawing.
What is Area?Area of a two dimensional shape is the total region which is bounded by the object's shape.
Given scale drawing can be made into two squares.
One with a side length of 1 inch and other with side length of 3 inches.
Area of a square with side length 'a' = a²
Area of the given scale drawing = (1 inch)² + (3 inches)²
= 1 inch² + 9 inches²
= 10 inches²
If the scale is 1 inch = 4 feet,
Area of the actual deck = (1 × 4 feet)² + (3 × 4 feet)²
= 4² [(1 feet)² + (3 feet)²]
= 4² (10)
= 160 feet²
Area of the actual deck = 160 feet²
= 16 (Area of the scale drawing)
If the scale is 1 inch = k feet,
Area of the actual deck = k² ( Area of scale drawing)
= 10 k² square feet
Hence the area of the actual deck would be 10k² if the scale is 1 inch = k feet.
Learn more about Area here :
https://brainly.com/question/12916755
#SPJ9
During a typical football game, a coach can expect 3.2 injuries. Find the probability that the team will have at most 1 injury in this game.
Answers
The probability of the team having at most 1 injury in the game can be calculated using a Poisson distribution.
To find the probability of the team having at most 1 injury in a typical football game, we can use a Poisson distribution. The Poisson distribution is commonly used to model the occurrence of rare events, such as injuries in this case.
The parameter for the Poisson distribution is the average number of injuries per game, which is given as 3.2.
Let's denote the random variable X as the number of injuries in a game. We need to calculate the probability P(X ≤ 1), which represents the probability of having at most 1 injury.
Using the Poisson distribution formula, we can compute this probability:
P(X ≤ 1) = P(X = 0) + P(X = 1)
Using the Poisson probability mass function, we substitute the values into the formula and calculate the probability.
The result will be the probability that the team will have at most 1 injury in the game.
To learn more about “probability” refer to the https://brainly.com/question/13604758
#SPJ11
PLS HELP ME $!!!!!!!
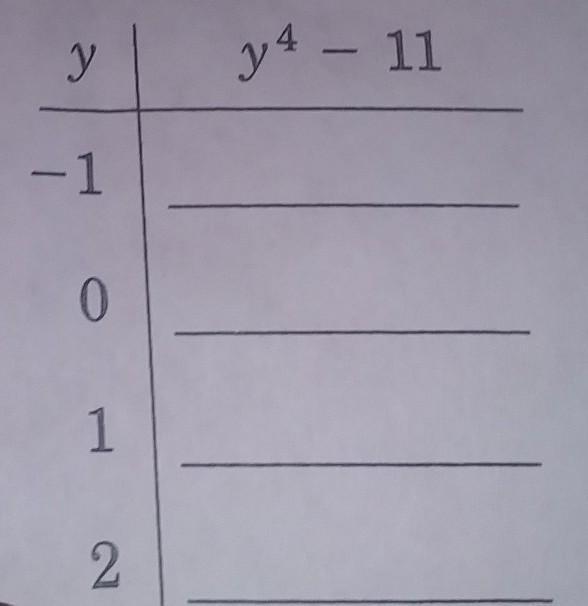
Answers
Step-by-step explanation:
(-1)⁴ - 11 = 1 - 11 = -10
0⁴ -11 = -11
1⁴ - 11 = -10
2⁴ -11 = -3
solve each equation in the real number system

Answers
Step-by-step explanation:
\( - x {}^{3 } - {x}^{2} + x + 1\)
\( - {x}^{2} ( x + 1) + 1(x + 1)\)
\((1 - {x}^{2} )(x + 1) = 0\)
\((1 - x)(1 + x)(x + 1) = 0\)
\(1- x = 0\)
\(x = 1\)
\(1 + x = 0\)
\(x = - 1\)
\(x = - 1\)
So we have the answer of
-1 and 1.
The following table gives information on GPAs and starting salaries (rounded to the nearest thousand dollars) of seven recent col- lege graduates.
GPA 2.90 3.81 3.20 2.42 3.94 2.05 2.25
Starting salary 48 53 50 37 65 32 37
Construct a 98% confidence interval for the mean starting salary of recent college graduates with a GPA of 3.15. Construct a 98% predic- tion interval for the starting salary of a randomly selected recent college graduate with a GPA of 3.15.
Answers
We can be 98% confident that the true mean starting salary of recent college graduates with a GPA of 3.15 lies between $36,540 and $55,740.
We can be 98% confident that the starting salary of a randomly selected recent college graduate with a GPA of 3.15 lies between -$32,080 and $124,360.
First, we need to calculate the sample mean, which is the average starting salary of the seven college graduates given:
sample mean = (48 + 53 + 50 + 37 + 65 + 32 + 37) / 7 = 46.14 thousand dollars
Next, we need to calculate the standard error. The sample standard deviation is calculated as follows:
s = √[((48-46.14)² + (53-46.14)² + (50-46.14)² + (37-46.14)² + (65-46.14)² + (32-46.14)² + (37-46.14)²) / 6] = 11.36 thousand dollars
The square root of the sample size is calculated as:
√(7) = 2.65
So, the standard error is:
standard error = 11.36 / 2.65 = 4.28 thousand dollars
Finally, we need to find the t-value for a 98% confidence level and 6 degrees of freedom (sample size - 1). We can use a t-table or a calculator to find this value, which is approximately 2.447.
Now we can plug in all the values into the formula to get the confidence interval:
Confidence interval = 46.14 ± 2.447 * 4.28 = (36.54, 55.74)
The t-value and standard error are calculated in the same way as in the confidence interval, but we also need to calculate the sample standard deviation, which is the square root of the variance:
variance = [(48-46.14)² + (53-46.14)² + (50-46.14)² + (37-46.14)² + (65-46.14)² + (32-46.14)² + (37-46.14)²] / 6
= 1315.43 thousand dollars squared
sample standard deviation = √(variance) = 36.26 thousand dollars
Now we can plug in all the values into the formula to get the prediction interval:
Prediction interval = 46.14 ± 2.447 * 4.28 ± 2.447 * 36.26 = (-32.08, 124.36)
To know more about confidence interval here
https://brainly.com/question/24131141
#SPJ4
There is an error in this diagram. What is the error and what have you learned that supports your answer?

Answers
The angles can't be the same and why is point f left alone?
If there are 3 apples for every 4 oranges, how many apples would you have if you had 20 oranges?
Answers
Answer:
6 Apples
Step-by-step explanation:
There would be six apples and 2 oranges left over.
Hope this Helps!
:D
Answer:
I was kind of confused on this one but is it 15 apples?
Step-by-step explanation:
3, 6, 9, 12, 15
4, 8, 12, 16, 20
I think the answer is 15 apples.
Marshall bought 32 ounces of mixed nuts, which are estimated to be 30% peanuts. Which expression can be used to find the percentage of peanut concentration of the final mix if he adds x ounces of peanuts?
Answers
Multiplying the entire expression by 100 gives us the percentage of peanut concentration in the final mix.
To find the percentage of peanut concentration in the final mix after Marshall adds x ounces of peanuts, we can use the following expression:
((0.3 * 32) + x) / (32 + x) * 100
Let's break down the expression:
0.3 * 32 represents the number of ounces of peanuts initially present in the mixed nuts. Since the mixed nuts are estimated to be 30% peanuts, multiplying 0.3 by the total weight of 32 ounces gives us the initial amount of peanuts
Adding x to this expression represents the additional ounces of peanuts that Marshall adds to the mix.
The denominator (32 + x) represents the total weight of the final mix, which includes both the initial mixed nuts (32 ounces) and the additional x ounces of peanuts.
For more such questions on percentage
https://brainly.com/question/24304697
#SPJ8
5 2/3 divided by what is 1?
Answers
Answer:
5 2/3
Step-by-step explanation:
I'm not sure how to explain, but 5 2/3 divided by itself is 1...
I hope this helped a little bit still. Have a great day c:
hope this helped:)
A vase contains 16 roses, 10 carnations, and 14 daisies. Write each ratio in lowest terms using carnations to all flowers
Answers
The ratio of carnations to all flowers in the vase is 1:4.
To find the ratio of carnations to all flowers, we need to compare the number of carnations to the total number of flowers in the vase.
Count the total number of flowers in the vase.
The vase contains 16 roses, 10 carnations, and 14 daisies. Adding these numbers together, we get a total of 40 flowers.
Determine the ratio of carnations to all flowers.
Out of the total 40 flowers, we have 10 carnations. Therefore, the ratio of carnations to all flowers can be expressed as 10:40.
Simplify the ratio to its lowest terms.
To simplify the ratio, we can divide both numbers by their greatest common divisor (GCD), which in this case is 10. Dividing 10 by 10 gives 1, and dividing 40 by 10 gives 4. Hence, the simplified ratio is 1:4.
Learn more about ratio
brainly.com/question/13419413
#SPJ11
To the nearest millimeter, a cell phone is 105 mm long and 66 mm wide. What is the ratio of the width to the length?
Answers
Answer:
22/35
Step-by-step explanation:
width/length = 66/105 = 22/35
Answer:
66/105
it says width to the length
not length to length
Please help me this is timed giving brainiest if right and 14 points (sorry it's all I have) :)

Answers
The given expressions and their verbal descriptions (meaning) are as follows;
2•(x - 3) → Twice the difference between x and 3\(x + \frac{3}{4} \) → Three fourths more than x. '5 + x' → The sum of five and the number, x\( \frac{3}{4} \cdot x\) → Three fourths part of x.5 - x → five less xx - 5 → Five less than x2•x - 3 → Twice x minus three\( \frac{5}{x} \) → The quotient of 5 and xHow can the expressions be described verbally?The given mathematical expressions and their correct verbal expressions or meaning are as follows;
2•(x - 3) can be described as two times or twice the difference between x and 3
\(x + \frac{3}{4} \)
The above mathematical expression can be described as three fourths added to x, which is the same as; three fourths more than x.
'5 + x' can be described as the sum of five and x, which is the same as the sum of five and the number, x.
\( \frac{3}{4} \cdot x\), The expression means the product of three fourths and x, which is the same as three fourths part of x.
5 - x can be written as the difference between five and x, which is the same as five less x
x - 5 can be written as the difference between x and 5, which means a number that is 5 less than x
2•x - 3 can be written as two times x minus three, which can be described as twice x minus three
\( \frac{5}{x} \) can be written as fI've divided by x. which can be written as the quotient of 5 and x
Learn more about verbal description mathematical expressions here:
https://brainly.com/question/9177302
#SPJ1
The radius of a circle is 18 yards. What is the circle's area?
Use 3.14 for .
Answers
Solution:
We know that:
Radius: 18 yardsπr² = Area of circleπ = 3.14Finding the area of the circle:
(π)(r²) = Area of circle=> (3.14)(18²) = Area of circle=> (3.14)(324) = Area of circle=> Area of circle = 3.14 x 324 = 1017.36 yards²\( \large{|\underline{\mathbb{\red{G}\blue{I}\orange{V}\pink{E}\blue{N}\purple{}\green{ : }\red{}\blue{}\orange{-}}}}\)
Radius = 18 yards\( \large{|\underline{\mathbb{\red{T}\blue{O }\orange{ \: }\pink{ F}\blue{I}\purple{N}\green{D }\red{ : }\blue{ - }\orange{-}}}}\)
Area of circle\( \underbrace{\mathbb{CALCULATION}}\)
\( \qquad \sf \dashrightarrow \: Area\:of \:circle = \pi {r}^{2} \)
\( \qquad \sf \dashrightarrow \: Area\:of \:circle = 3.14 \times {18}^{2} \)
\( \qquad \sf \dashrightarrow \: Area\:of \:circle = 3.14 \times 324\)
\( \qquad \sf \dashrightarrow \: Area\:of \:circle = 1017.36\)
Thus, The area of the circle is 1017.36 yard²...~
factor the trinomial. use the steps and factor chart for help. x2 5x 6x2 5x 6 remember the format: ax2 bx c
Answers
After factorizing the trinomial x^2 - 5x + 6 the factors are ( x - 3 ) ( x - 2).
Given:
Quadratic equation:
x^2 - 5x +6
= x^2 - 3x - 2x +6
Taking x as common
= x ( x - 3 ) - 2x + 6
Taking -2 as common
= x ( x - 3 ) - 2 ( x - 3 )
Taking (x-3) as common
= ( x - 3 ) ( x - 2 )
Therefore after factorizing the trinomial x^2 - 5x + 6 the factors are
( x - 3 ) ( x - 2).
Learn more about the factor here:
https://brainly.com/question/26923098
#SPJ4
Find the area of the surface.
The part of the hyperbolic paraboloid z = y2 − x2 that lies between the cylinders x2 + y2 = 1 and x2 + y2 = 4
Answers
The area of the surface between the cylinders x2 + y2 = 1 and x2 + y2 = 4 for the hyperbolic paraboloid z = y2 - x2 is 3π√(17).
Hyperbolic paraboloid is a doubly ruled surface that can be described as a saddle-shaped surface that has hyperbolic curves in two different directions and parabolic curves in the third. It can be represented by the equation z = x2 - y2 or z = y2 - x2, depending on the orientation of the surface.Let's take the hyperbolic paraboloid z = y2 - x2, the part of the hyperbolic paraboloid that lies between the cylinders x2 + y2 = 1 and x2 + y2 = 4 is shown below:
Let's solve the problem now:
We can evaluate the surface area of this region using a double integral in cylindrical coordinates:
∫∫R √(1 + fx2 + fy2) dA, where f is the function z = y2 - x2, and R is the region of integration.
For this particular problem, R is the annular region between the cylinders x2 + y2 = 1 and x2 + y2 = 4, and it can be expressed as 1 ≤ r ≤ 2, 0 ≤ θ ≤ 2π. Therefore, we have:
∫∫R √(1 + fx2 + fy2) dA= ∫02π ∫12^2 √(1 + (−2x)2 + (2y)2) rdrdθ
= ∫02π ∫12^2 √(17) rdrdθ= √(17) ∫02π ∫12^2 rdrdθ
= √(17) ∫02π [r2/2]12^2 dθ= √(17) ∫02π (4 − 1)/2 dθ
= √(17) ∫02π 3/2 dθ= 3π√(17).
Therefore, the area of the surface between the cylinders x2 + y2 = 1 and x2 + y2 = 4 for the hyperbolic paraboloid z = y2 - x2 is 3π√(17).
To know more about hyperbolic paraboloid visit:
https://brainly.com/question/14786349
#SPJ11
Find distance between the parallel lines
L1
x=−3−2t,y=5+3t,z=−2−t
L2
X=−2+2s,y=−2−3s,z=3+s.
Answers
We can find the distance between the two parallel lines L1 and L2 by using the formula: d = |a (x1 - x2) + b (y1 - y2) + c (z1 - z2)| / √(a2 + b2 + c2), where a, b, and c are the direction ratios of the two parallel lines, and (x1, y1, z1) and (x2, y2, z2) are two points on the two lines. Using the given direction ratios and points, we can calculate the distance between the two parallel lines.
The direction ratios of line L1 are (-2, 3, -1), and the direction ratios of line L2 are (2, -3, 1). Let (x1, y1, z1) be the point (-3, 5, -2) on L1, and (x2, y2, z2) be the point (-2, -2, 3) on L2. Then, the distance between the two lines is:d = |a (x1 - x2) + b (y1 - y2) + c (z1 - z2)| / √(a^2 + b^2 + c^2)Where a, b, and c are the direction ratios of the two parallel lines. Plugging in the values, we get:d = |(-2)(-3 + 2s) + (3)(5 + 3t + 2) + (-1)(-2 - t - 3)| / √((-2)^2 + 3^2 + (-1)^2)This simplifies to:d = |-4s + 19 + t - 3| / √14Therefore, the distance between the two parallel lines is |4s + t - 16| / √14.
Learn more about direction ratios here:
https://brainly.com/question/11909679
#SPJ11
"What is the global minimum of the function f(x)=x^2/2-x, on the
interval 0 ≤ x ≤ 3 ?
Answers
The global minimum of the function f(x) = x^2/2-x on the interval 0\(\leq\) x\(\leq\) 3 occurs at x = 1 with a value of f(1) = -0.5.
The global minimum of the function f(x)=x^2/2-x on the interval 0 ≤ x ≤ 3 can be found by taking the derivative of the function and setting it equal to zero to find the critical points.
f'(x) = x - 1 = 0
x = 1
We then need to check the endpoints of the interval to see if they are lower than the critical point:
f(0) = 0
f(3) = 9/2 - 3 = 3/2
Comparing the values, we see that the global minimum of the function on the interval 0 ≤ x ≤ 3 is f(1) = 1/2.
Visit here to learn more about Function:
brainly.com/question/11624077
#SPJ11
in a two-way analysis of variance, a researcher tests for the significance of: group of answer choices three main effects. one main effect and an interaction. two interactions. two main effects and an interaction.
Answers
In a two-way analysis of variance, a researcher tests for the significance of two main effects and an interaction.
What is two-way analysis of variance?A statistical test called two-way analysis of variance (ANOVA) compares the means of many groups using two independent variables (factors) and one dependent variable.
In a two-way analysis of variance (ANOVA), the researcher tests for the significance of two main effects and an interaction effect between two independent variables (factors) on a dependent variable. The main effects refer to the individual effect of each factor on the dependent variable, while the interaction effect refers to the combined effect of both factors on the dependent variable. Thus, the researcher aims to examine how each independent variable affects the dependent variable separately (main effects) and how their combination affects the dependent variable (interaction effect).
Therefore, in a two-way analysis of variance, a researcher tests for the significance of two main effects and an interaction.
Learn more about two-way analysis of variance on:
https://brainly.com/question/29435977
#SPJ4