The ratio of an objects weight on earth to its weight on the moon is 6:1 the first person to walk on the moon was neil armstrong. he weighed 165 pounds on earth. what would be the proportion of this word problem?
Answers
The proportion of this word problem is 6 : 1 where Neil Armstrong weighed approximately 27.5 pounds on the moon.
The proportion of a word problem represents the relationship between two or more quantities. In this case, the proportion can be set up as:
Weight on Earth : Weight on Moon = 6 : 1
Using the information provided in the problem, we know that Neil Armstrong weighed 165 pounds on Earth. We can use this information to find his weight on the moon by setting up a proportion:
165 : x = 6 : 1
where x represents his weight on the moon. To solve for x, we can cross-multiply and simplify:
165 * 1 = 6 * x
x = 165/6
x ≈ 27.5
Therefore, Neil Armstrong weighed approximately 27.5 pounds on the moon.
Learn more about weight at https://brainly.com/question/21086815
#SPJ11
Related Questions
Tell whether the angles are complementary or supplementary. Then find the value of x.
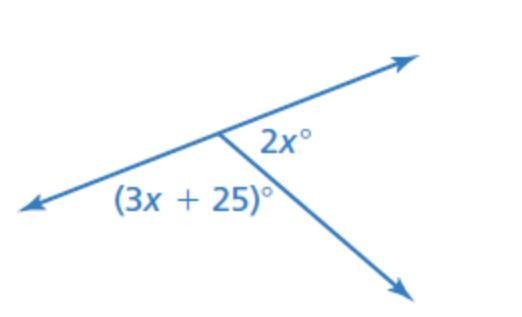
Answers
3x+25+2x=180
5x=155
x=31
Hope this helps!! :)
Pick an lunch for every single day?



Answers
Answer:
The last one please.
3x-2
3
= 9
4x-1 what is the answer
Answers
Answer:
\(-\frac{22}{91} = x\)
Step-by-step explanation:
To solve the equation \(3x - 23 = 94x - 1\), we'll follow these steps:
Start by simplifying the equation by combining like terms. In this case, we have terms with x on both sides, as well as constants:
\(3x - 23 = 94x - 1\)
To isolate the x terms, we can subtract 3x from both sides of the equation:
\(3x - 3x - 23 = 94x - 3x - 1\)
Simplifying further, we get:
\(-23 = 91x - 1\)
Next, we want to isolate the constant term on one side of the equation. We can do this by adding 1 to both sides:
\(-23 + 1 = 91x - 1 + 1\)
Simplifying further:
\(-22 = 91x\)
Finally, we can solve for x by dividing both sides of the equation by 91:
\(-\frac{22}{91}=\frac{91x}{91}\)
Simplifying further:
\(-\frac{22}{91} = x\)
Therefore, the solution to the equation \(3x - 23 = 94x - 1\) is \(-\frac{22}{91} = x\)
help me with is please the question is in the picture

Answers
$1.60 x .10 = .16
1.60 - .16 = $1.44
so
1.44 x 4 = $5.76
1.44 / 2 = .72
$5.76 + .72 = $6.48
so your answer is $6.48 [B]
Answer: the answer is b or 6.48
Step-by-step explanation:
Find q in this geometry problem please.

Answers
Answer:
3
Step-by-step explanation:
Use scale factor
6/q=8/4
a car is to be placed on a metal incline for display. if only friction is to be used to keep the car at rest on the incline, what is the maximum angle theta of the incline if, for the car on the incline, the coefficient of static friction is 0.8 and the coefficient of kinetic friction is 0.6?
Answers
The maximum angle of the incline for the car to be at rest using only friction is 38.7° if, for the car on the incline, the coefficient of static friction is 0.8 and the coefficient of kinetic friction is 0.6.
If the car is at rest on the incline, the force of gravity acting on the car down the incline is balanced by the force of static friction acting up the incline. The maximum angle \($\theta$\) of the incline is the angle at which the force of static friction is at its maximum, which is given by the product of the coefficient of static friction and the normal force.
Let's assume that the mass of the car is m and the incline makes an angle of \($\theta$\) with the horizontal. Then, the force of gravity acting on the car down the incline is given by \($mg\sin(\theta)$\), where g is the acceleration due to gravity. The normal force acting on the car perpendicular to the incline is given by \($mg\cos(\theta)$\).
For the car to be at rest on the incline, the force of static friction acting up the incline must be equal in magnitude to the force of gravity down the incline. Therefore, we have:
\($$\mu_s mg\cos(\theta) = mg\sin(\theta)$$\)
here \($\mu_s$\) is the coefficient of static friction. Simplifying this equation,
we get:
\($$\tan(\theta) \leq \mu_s$$\)
Therefore, the maximum angle \($\theta$\) of the incline is:
\($$\theta \leq \tan^{-1}(\mu_s)$$\)
Substituting the value of \($\mu_s = 0.8$\), we get:
\($$\theta \leq \tan^{-1}(0.8) \approx 38.7^{\circ}$$\)
Therefore, the maximum angle of the incline for the car to be at rest using only friction is approximately 38.7°.
To read more about static friction:
https://brainly.com/question/13000653
#SPJ4
An ordered pair is a(n) ________ of an equation in two variables if replacing the variables by the coordinates of the ordered pair results in a true statement.
Answers
An ordered pair is a solution of an equation in two variables if replacing the variables by the coordinates of the ordered pair results in a true statement.
In mathematics, an equation in two variables represents a relationship between two quantities. An ordered pair consists of two values, typically denoted as (x, y), that represent the coordinates of a point in a two-dimensional plane.
When these values are substituted into the equation, if the equation holds true, then the ordered pair is considered a solution or a solution set to the equation. This means that the relationship described by the equation is satisfied by the values of the ordered pair. In other words, the equation is true when evaluated with the values of the ordered pair.
Learn more about ordered pair at https://brainly.com/question/29427152
#SPJ11
Perpendicular distance between the base of a triangle and the opposite vertex is called _____of the triangle
Answers
Answer:
Median might be the answer or maybe the height?
at what rate is the area of the triangle formed by the ladder wall and ground changing when the top of the ladder is 12 m from the ground?
Answers
The rate of change of the area of the triangle is not constant and will depend on the angle between the ladder and the ground.
Rate of Change of Area of Triangle Formed by Ladder Wall and Ground with 12 m Top of LadderThe area of the triangle formed by the ladder wall and ground is dependent on the angle between the ladder and the ground. The area of a triangle is equal to half the product of the length of the base and the corresponding height. Therefore, if the angle between the ladder and the ground changes, the corresponding height of the triangle will also change, resulting in a change of the area of the triangle. As the angle between the ladder and the ground changes, the rate of change of the area of the triangle will also change.
Learn more about the Area of Triangle: https://brainly.com/question/17335144
#SPJ4
Can someone help with this

Answers
Answer:
1/8^2, 1/2^4 and 1/3^5
Step-by-step explanation:
¡¡ANSWER MY QUESTION FIRST¡¡
Can you help me with these questions, please?


Answers
Answer:
∠5 = 70°
∠8 = 130°
Step-by-step explanation:
Since ∠5 and ∠1 are equal they will both equal 70°
Since ∠6 and ∠8 are also equal they will both equal 130°
Hope this helps
Plz mark brainliest
Help me please I really need it please help me

Answers
The answer is in the image. If you convert them to improper fractions, the division is easier. Like 2/3 + 1 = 5/3

Solve the system by graphing, then state the solution as an ordered pair
HELP ASAP!!!!!

Answers
Step-by-step explanation:
Simply graph the two equations....the intersection of the two graphs is the solution

Marcy walked 3 7/10 miles on Saturday and Sunday she walked 0.25 more miles than she did on Saturday how many total miles did she walk over the weekend. Pls.
Help
It’s math
B
Answers
Over the weekend she walked a total distance of (4 + 5/8) miles
How many total miles did she walk over the weekend?
We know that on Saturday she walked a total of (3 + 7/10) miles (so we need to work with mixed numbers), and on Sunday she walked 0.25 of that distance.
Then the distance that she walked on Sunday is:
D = 0.25*(3 + 7/10) miles
We can rewrite: 0.25 = 1/4
replacing that:
D = (1/4)*(3 + 7/10) mi = (3/4 + 7/40) mi
= (30/40 + 7/40)mi = (37/40)mi
Then the total distance that she walked over the weekend is:
d = (3 + 7/10) mi + (37/40)mi
= (120/40 + 28/40) mi + (37/40) mi
= (185/40)mi = (160/40 + 25/40) mi = (4 + 5/8) mi
Over the weekend she walked a total distance of (4 + 5/8) miles
If you want to learn more about mixed numbers:
https://brainly.com/question/21610929
#SPJ1
Solve 2x 10 = -4
X = ?
Answers
2x • 10 = -4
20x = -4
x = - 4/20 = -0.2
Answer: x = -0.2
I need help with this

Answers
Step-by-step explanation:
\( {17}^{2} = {8}^{2} + {b}^{2} \\ {b}^{2} = {17}^{2} - {8}^{2} \\ {b }^{2} = 225 \\ b = \sqrt{225} = 15\)
Use Pythagorean theorem
\(\\ \sf\longmapsto b^2=h^2-p^2\)
\(\\ \sf\longmapsto b^2=17^2-8^2\)
\(\\ \sf\longmapsto b^2=289-64\)
\(\\ \sf\longmapsto b^2=225\)
\(\\ \sf\longmapsto b=15ft\)
I need help with this question

Answers
Answer:
Step-by-step explanation:

Listed below are the results of 16 independent trials that attempted to measure quantity Q. Calculate the average value and give an uncertainty range where you can be 95% sure that the true value of Q lies within.41.31440.08741.24840.19640.28441.15238.85236.40137.94139.22139.03538.40440.68341.56842.17542.319calculate the absolute value of the difference in the two estimates of q with an uncertainty range at a 95onfidence interval. make sure you do all calculations with unrounded values.
Answers
Note that the absolute value of the difference in the two estimates of Q with an uncertainty range at a 95% confidence interval is 1.052.
What is the rationale for the above response?To find the average value of Q, we simply add up all the values and divide by the number of trials:
Average value of Q = (41.314 + 40.087 + 41.248 + 40.196 + 40.284 + 41.152 + 38.852 + 36.401 + 37.941 + 39.221 + 39.035 + 38.404 + 40.683 + 41.568 + 42.175 + 42.319)/16
= 39.976
Next, to find the uncertainty range where we can be 95% sure that the true value of Q lies within, we need to find the standard error of the mean. The formula gives this:
Standard error of the mean = standard deviation / √(n)
where n is the number of trials. We can find the standard deviation using the formula:
Standard deviation = √(Σ(Qi - Q_avg)² / (n-1))
where Qi is the value of Q for the ith trial.
Using these formulas, we find:
Standard deviation = 1.549
Standard error of the mean = 0.387
To find the uncertainty range, we say:
Uncertainty range = t-value * standard error of the mean
= 2.131 * 0.387
= 0.826
Therefore, we can be 95% sure that the true value of Q lies within the range:
39.976 ± 0.826
Now, to calculate the absolute value of the difference in the two estimates of Q with an uncertainty range at a 95% confidence interval, we can simply add the uncertainty ranges of the two estimates and take the absolute value of the difference:
|Q1 - Q2| = |39.976 ± 0.826 - 40| + |39.976 ± 0.826 - 39.8|
= 0.826 + 0.226
= 1.052
Therefore, the absolute value of the difference in the two estimates of Q with an uncertainty range at a 95% confidence interval is 1.052.
Learn more about Absolute Value at:
https://brainly.com/question/1301718
#SPJ1
I MARKING BRAINLIST! "If you cry me a river, then I'll give you a tissue." is this sentence complex, compound or simple? Also, tell me what the dependent clause is and the independent clauses.
Answers
Which is the graph of the rose curve


Answers
Rose curve equations have two forms: r = a cos(nθ) and r = a sin(nθ) where a ≠ 0 and n is a positive integer. Petals have length determined by a. If n is odd, the number of petals is n. However, if n is even, the number of petals is 2n.
hope it helps aaa ^^'

AB=x+25, AC=26, and BC= 29 + x. Find x.
Answers
Answer:
-14Step-by-step explanation:
Given
AB=x + 25, AC=26, BC= 29 + xAs per segment addition postulate
AB + BC = ACSubstituting values
x + 25 + 29 + x = 262x = -28x = -147(x+4)=-21
what does x equals
CORRECT answers ONLY please
Answers
Answer: x = -7
Step-by-step explanation:
7 (x + 4) = -21
7x + 28 = -21
Subtract 28 from both sides
7x = -49
Divide both sides by 7
x = -7
Answer:
x = -7
Step-by-step explanation:
first distribute he 7 to get 7x + 28 = -21
then subtract 28 from both sides to get 7x = -49
lastly divide 7 from both sides to get x = -7
At the market, Meyer buys a bunch of bananas for $0.65 per pound and a frozen pizza for $4.99. The total for his purchase was $6.94, without tax. How many pounds of bananas did Meyer buy?
Answers
Answer:
Well, 6.94 - 4.99 = 1.95 also that divided by 0.65 = 3 So it is 3 pounds of bananas
Step-by-step explanation:
P.S can I have brainliest?
6.94-4.99=1.95
1.95*0.65=3
3
Write an equation in slope-intercept form for the line with slope 1/5
and y-intercept 5.
Answers
Answer:
y=1/5x+5
Step-by-step explanation:
Slope-intercept form is written y=mx+b.
y- needs to be by itself in this form.
m- the slope.
x- always to the right side of the slope, or m.
b- y-intercept.
Now that we know this, all we have to do is plug in the numbers we have. So when we plug this in, the equation looks like this:
y=1/5x+5
Hope this helps you and have a great day :3
6. The diagram on the right shows right-angled triangles POR
and PRS. Given that tan 0 =
3
4
in em, the length of
(a) PR
(b) RS
Q
9 cm
R
Answers
Answer:
The answer is below
Step-by-step explanation:
Trigonometric ratios shows the relationship between the sides of a right angled triangle and its angles. Some trigonometric ratios are:
sinθ = opposite / hypotenuse, cosθ = adjacent / hypotenuse; tanθ = opposite / adjacent.
In triangle PQR:
tanθ = QR / PQ
substituting gives:
3/4 = 9 / PQ
PQ = 9 * 4 / 3 = 12 cm
Applying Pythagoras in triangle PQR gives:
PR² = PQ² + QR²
PR² = 12² + 9²
PR² = 144 + 81 = 225
PR = 15 cm
Also in triangle PRS:
PS = (5/3)PR = (5/3)*15 = 25 cm
PS² = PR² + RS²
25² = 15² + RS²
625 = 225 + RS²
RS² = 400
RS = 20 cm


the midpoint of chord AB is ( , ), and the slope of chord AB is BLANK
Answers
Answer:
midpoint of chord ab is (-2, 12) slope of chord ab is 1/2
Step-by-step explanation:
pls help
Factor out the GCF
16x - 48
Answers
Answer:
16
Step-by-step explanation:
the greatest common factor of 16 and 48 is 16
Factors for 16: 1, 2, 4, 8, and 16.
Factors for 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
Find the solution of the differential equation r ′′
(t)=⟨e 10t−10
,t 2
−1,1⟩ with the initial conditions r(1)=⟨0,0,5⟩,r ′
(1)=⟨12,0,0⟩ (Use symbolic notation and fractions where needed. Give your answer in vector form.) r(1
Answers
The solution to the differential equation is: r(t) = ⟨1/100 e10t - t2 + 119/10 t + 49/100, 1/12 t4 - 1/2 t2 - 13/3 t - 1/3, 1/2 t2 - 12 t + 26/5 ⟩, for t ≥ 0.
The differential equation for r′′(t) = ⟨e10t − 10, t2 − 1, 1⟩ with the initial conditions r(1) = ⟨0, 0, 5⟩, r′(1) = ⟨12, 0, 0⟩ can be solved using the following method:
Solve for the position vector r(t) using the acceleration vector a(t).
Then solve for the velocity vector r′(t) using the initial velocity. Finally, solve for r(t) using the initial position vector.1.
Solve for r(t) using a(t)
Integrate a(t) with respect to t two times to get r(t):a(t) = ⟨e10t − 10, t2 − 1, 1⟩
Integrating once will give the velocity: v(t) = ∫a(t) dt = ⟨ 1/10 e10t - 10t + C1 , 1/3 t3 - t + C2, t + C3 ⟩
Integrating again will give the position: r(t) = ∫v(t) dt = ⟨ 1/100 e10t - t2 + C1t + C4 , 1/12 t4 - 1/2 t2 + C2t + C5, 1/2 t2 + C3t + C6 ⟩2.
Solve for C1, C2, and C3 using initial velocity r′(1) = ⟨12, 0, 0⟩ = v(1)C1 = 119/10, C2 = -13/3, C3 = -12.3.
Solve for C4, C5, and C6 using initial position r(1) = ⟨0, 0, 5⟩ = r(1)C4 = 49/100, C5 = -1/3, C6 = 26/5
Therefore, the solution to the differential equation is: r(t) = ⟨1/100 e10t - t2 + 119/10 t + 49/100, 1/12 t4 - 1/2 t2 - 13/3 t - 1/3, 1/2 t2 - 12 t + 26/5 ⟩, for t ≥ 0.
Learn more about: differential equation
https://brainly.com/question/21145944
#SPJ11
Z+k, when z=1 and k = 7
Answers
Answer:
8
Step-by-step explanation:
Replace the variables with numbers.
1+7=8
Answer:
8
Step-by-step explanation:
Since z equals 1 and k equals 7, we do 1 + 7 which is equal to 8. Therefore, the answer would be 8.
Tema: valor numérico de expresiones algebraicas
A= 2
B= 1
X= 3
Y= 5
Z= -3

Answers
Answer:
1. 61
2. -8
3. 731
4. -16
5. -5
Step-by-step explanation: