The total amount of the food came to $47. 50. But the restaurant also charges 6% sales tax on the total. The server was not great, so you left a 15% tip. How much will they pay at the restaurant’s register, including sales tax and tip?
Answers
The pay at the restaurant’s register, including sales tax and tip will be $ 57.475.
The sales tax amount = 47.50 × 6%
Calculating percentage on Right Hand Side of the equation
The sales tax amount = 2.85
Total amount of bill and sales tax = 47.50 + 2.85
Performing addition on Right Hand Side of the equation
Total amount of bill and sales tax = $50.35
Tip amount = 47.50 × 15%
Performing multiplication on Right Hand Side of the equation
Tip amount = 7.125
Total amount of bill and sales tax = 50.35 + 7.125
Performing addition on Right Hand Side of the equation
Total amount of bill and sales tax = $57.475
Hence, the total pay is $ 57.475.
Learn more about percentage -
https://brainly.com/question/24877689
#SPJ4
Related Questions
A painter spends 3 hours working on a painting. A sculptor spends 23 as long working on a sculpture. How long does the sculptor work?
Answers
Answer:
69 hours
Step-by-step explanation:
The painter spends 3 hours working on a painting.
The sculptor spends 23 times as long as the painter.
The amount of time the sculptor spent is:
23 * 3 = 69 hours
The sculptor works for 69 hours.
What is the area of the triangle?
4
2
units
Lol been struggling on this for a while

Answers
I NEED THE ANSWER TO THIS BY TODAY PLEASE HELP (200, 150) GCF
Answers
Answer: 50
Step-by-step explanation:
Greatest common factor of 200 and 150 is 50
200/50=4
150/50=3
does anyone know the answer?????

Answers
Answer:
-3x + 7
Step-by-step explanation:
she used the y-intercept as the slope and the slope as the y- intercept.
Answer:
its y= -3x+7
Step-by-step explanation:
she used the x intercept for the y - intercept and the y- intercept for the c-intercept
What is the value of x?
А
6x - 3
3x + 6
B
5x

Answers
Answer:
x=3
Step-by-step explanation:
6x-3
(6*3)-3
18-3
15
3x+6
(3*3)+6
9+6
15
5x
5*3
15
The value of x from the given equilateral triangle is 3.
The given triangle is equilateral triangle with sides 6x-3, 3x+6 and 5x.
What is an equilateral triangle?An equilateral triangle is a triangle in which all three sides are equal and angles are also equal. The value of each angle of an equilateral triangle is 60° therefore, it is also known as an equiangular triangle.
Now, 6x-3=3x+6
⇒ 6x-3x=6+3
⇒ 3x=9
⇒ x=9/3 =3
and 6x-3=5x
⇒ 6x-5x=3
⇒ x=3
Therefore, the value of x from the given equilateral triangle is 3.
To learn more about an equilateral triangle visit:
https://brainly.com/question/17824549.
#SPJ2
Worth 60 points for a rapid reply- find the area of each regular polygon. Answers are rounded to the nearest whole number.

Answers
The area of the regular polygons with 12 sides(dodecagon) and 5 sides (pentagon) are 389.06 in² and 19.87 in² respectively.
How to calculate for the area of the polygonArea of regular polygon = 1/2 × apothem × perimeter
perimeter = (s)side length of octagon × (n)number of side.
apothem = s/[2tan(180/n)].
11 = s/[2tan(180/12)]
s = 11 × 2tan15
s = 5.8949
perimeter = 5.8949 × 12 = 70.7388
Area of dodecagon = 1/2 × 11 × 70.7388
Area of dodecagon = 389.0634 in²
Area of pentagon = 1/2 × 5.23 × 7.6
Area of pentagon = 19.874 in²
Therefore, the area of the regular polygons with 12 sides(dodecagon) and 5 sides (pentagon) are 389.06 in² and 19.87 in² respectively.
Read more about area here:https://brainly.com/question/27440983
#SPJ1
Education researchers are interested in the workload expectations of freshmen at a local university. Since all of the
freshmen are randomly placed into freshman seminar classes the researchers randomly select 3 freshman seminar
classes and survey all of the students within those classes. Which sampling method was used?
Answers
Answer: cluster sampling
Step-by-step explanation: got it right on edge:)
Answer:
A
Step-by-step explanation:
find an equation of the tangent line to the given curve at the specified point. y = e^x / x , (1, e)
Answers
y = e is the equation of the tangent line to the given curve at the specified point , y = \(e^{x}\) / x , (1, e)
Through the coordinate geometry formal of point-slope form, the equation of tangent and normal can be calculated.
The tangent has the equation (y - y1) = m(x - x1), and a normal travelling through this point and perpendicular to the tangent has the equation (y - y1) = -1/m (x - x1).
thus , y' = \(\frac{e^{x}-xe^{x} }{x^{2} }\)
y'(1) = 0 = m
Our slope is indicated by the horizontal line.
y−\(y_{1}\)=m(x−\(x_{1}\))
Our line will simply be our y-coordinate because our slope(m) is 0:
e
Therefore:
The tangent line's equation is y=e.
For more such questions on Tangent :
brainly.com/question/14022348
#SPJ4
Use Heron's Area Formula to find the area of the triangle. (Round your answer to two decimal places.) \[ a=11.52, \quad b=7.62, c=14.5 \]
Answers
The area of the triangle is 42.31 square units.Using Heron's formula, we found that the area of the triangle with side lengths a = 11.52, b = 7.62, and c = 14.5 is approximately 42.31 square units.
To find the area of the triangle using Heron's formula, we need to calculate the semi-perimeter (s) first. The semi-perimeter is given by the formula s = (a + b + c) / 2, where a, b, and c are the lengths of the sides of the triangle.
In this case, we have a = 11.52, b = 7.62, and c = 14.5. Thus, the semi-perimeter is:
s = (11.52 + 7.62 + 14.5) / 2 = 33.64 / 2 = 16.82.
Now, we can use Heron's formula to calculate the area (A) of the triangle:
A = sqrt(s(s - a)(s - b)(s - c)).
Substituting the values, we have:
A = sqrt(16.82(16.82 - 11.52)(16.82 - 7.62)(16.82 - 14.5))
A = sqrt(16.82(5.3)(9.2)(2.32))
A = sqrt(424.469728) ≈ 20.61.
Rounding the area to two decimal places, the area of the triangle is approximately 42.31 square units.
Using Heron's formula, we found that the area of the triangle with side lengths a = 11.52, b = 7.62, and c = 14.5 is approximately 42.31 square units.
To know more about Heron's formula follow the link:
https://brainly.in/question/40915776
#SPJ11
he current in an rlc circuit is described by d2idt2 10didt 25 i = 0 if i(0) = 10 a and di(0)/dt = 0, then for t > 0, i(t) = (a bt)est a, where a = , b = , and s = .
Answers
The current in an rlc circuit is described by d²i/dt² + 10di/dt + 25i = 0 if i(0) = 10 a and di(0)/dt = 0, then for t > 0, where a = 10 , b = 5 , and s = -5.
The given differential equation is:
d²i/dt² + 10di/dt + 25i = 0
The characteristic equation is:
r² + 10r + 25 = 0
Solving this quadratic equation, we get:
r = (-10 ± √(100 - 4*25))/2
r = -5
Since the roots are equal, the general solution of the differential equation is:
i(t) = (a + bt) \(e^{-5t}\)
Now, using the initial conditions i(0) = 10 and di(0)/dt = 0, we get:
i(0) = a = 10
di/dt = -5(a + bt)e \(e^{-5t}\) + b* \(e^{-5t}\)
At t=0, di/dt = 0
So, 0 = -5a + b
b = 5a
Substituting the value of a and b, we get:
i(t) = (10 + 5t) \(e^{-5t}\)
Therefore, for t > 0, i(t) = (10 + 5t) \(e^{-5t}\).
Learn more about "RLC circuit": brainly.com/question/15595203
#SPJ11
n + n+1 = 2n+1 = 2n+2-1 = 2(n+1) -1
2 = factor so must be even.
even number -1 is always odd
Answers
The value of n is 1/2 and it is not an even number or odd number
How to determine the solution to the equation?From the question, the steps are given as
n + n + 1 = 2n + 1
n + n + 1 = 2n+2-1
n + n + 1 = 2(n+1) -1
Also, from the question, we have the result of the expression to be
2
This means that
n + n + 1 = 2
Substitute n + n + 1 = 2(n+1) -1 in the equation n + n + 1 = 2
So, we have
2(n + 1) - 1 = 2
Add 1 to all sides of the equation
So, we have
2(n + 1) = 3
Divide both sides of the equation by 2
So, we have
n + 1 = 3/2
Subtract 1 from all sides
n = 1/2
The above implies that the number n is neither an even number, nor an odd number
This is so because the result is a fraction
Read more about expressions at
https://brainly.com/question/13818690
#SPJ1
in a class there are 84 student . the number of boy is 2 times the number of girls .how many girls are there in the class
Answers
Answer:
28 girls.
Step-by-step explanation:
b - number of boys
g - number of girls
b = 2*g
b + g = 84
2*g + g = 84
3*g = 84
g = 84/3 = 28
And just in case:
b = 2*g = 2*28 = 56
b + g = 28 + 56 = 84; the answer checks out ;)
Answer:
28
Step-by-step explanation:
Let the number of girls be x .
number of boys = 2x
Number of students in class =84
A/q,
2x +x = 84
3x =84
x= 84/3
x= 28
So number of girls in class is 28
please give brainliest thank you
Anya has $25,000 which she recently received from a trust fund, which she intends to invest in an account earning 12% annually. a) How many years would it take Anya to accumulate $40,000. b) If Anya's goal is to save $40,000 in just 3 years, what rate of return must she earn annually on her account. Show all workings and formulae
Answers
a) It would take Anya approximately 4 years to accumulate $40,000 with an annual interest rate of 12%. b) Anya must earn an annual rate of return of approximately 12.6% to save $40,000 in 3 years.
a) To calculate the number of years it would take Anya to accumulate $40,000, we can use the future value formula for compound interest:
Future Value = Present Value * (1 + interest rate)ⁿ
Where:
Future Value = $40,000
Present Value = $25,000
Interest rate = 12% = 0.12
n = number of years
Substituting the given values into the formula, we have:
$40,000 = $25,000 * (1 + 0.12)ⁿ
Dividing both sides of the equation by $25,000, we get:
(1 + 0.12)ⁿ = 40,000 / 25,000
(1.12)ⁿ = 1.6
To solve for n, we can take the logarithm of both sides of the equation:
n * log(1.12) = log(1.6)
Using a calculator, we find that log(1.12) ≈ 0.0492 and log(1.6) ≈ 0.2041. Therefore:
n * 0.0492 = 0.2041
n = 0.2041 / 0.0492 ≈ 4.15
b) To calculate the required rate of return for Anya to save $40,000 in just 3 years, we can rearrange the future value formula:
Future Value = Present Value * (1 + interest rate)ⁿ
$40,000 = $25,000 * (1 + interest rate)³
Dividing both sides of the equation by $25,000, we have:
(1 + interest rate)³ = 40,000 / 25,000
(1 + interest rate)³ = 1.6
Taking the cube root of both sides of the equation:
1 + interest rate = ∛1.6
Subtracting 1 from both sides, we get:
interest rate = ∛1.6 - 1
Using a calculator, we find that ∛1.6 ≈ 1.126. Therefore:
interest rate = 1.126 - 1 ≈ 0.126
To express the interest rate as a percentage, we multiply by 100:
interest rate = 0.126 * 100 = 12.6%
To know more about annual interest rate,
https://brainly.com/question/33696451
#SPJ11
Find the maximums and minimums and where they are reached of the function f(x,y)=x2+y2+xy in {(x,y): x^2+y^2 <= 1
(i) Local
(ii) Absolute
(iii) Identify the critical points in the interior of the disk (not the border) if there are any. Say if they are extremes, what kind? Or saddle points, or if we can't know using one method?
Answers
To find the maximums and minimums of the function f(x,y)=x^2+y^2+xy in the region {(x,y): x^2+y^2<=1}, we need to use the method of Lagrange multipliers.
First, we need to find the gradient of the function and set it equal to the gradient of the constraint (which is the equation of the circle x^2+y^2=1).
∇f(x,y) = <2x+y, 2y+x>
∇g(x,y) = <2x, 2y>
So, we have the equations:
2x+y = 2λx
2y+x = 2λy
x^2+y^2 = 1
Simplifying the first two equations, we get:
y = (2λ-2)x
x = (2λ-2)y
Substituting these into the equation of the circle, we get:
x^2+y^2 = 1
(2λ-2)^2 x^2 + (2λ-2)^2 y^2 = 1
(2λ-2)^2 (x^2+y^2) = 1
(2λ-2)^2 = 1/(x^2+y^2)
Solving for λ, we get:
λ = 1/2 or λ = 3/2
If λ = 1/2, then we get x = -y and x^2+y^2=1, which gives us the critical points (-1/√2, 1/√2) and (1/√2, -1/√2). We can plug these into the function to find that f(-1/√2, 1/√2) = f(1/√2, -1/√2) = -1/4.
If λ = 3/2, then we get x = 2y and x^2+y^2=1, which gives us the critical point (2/√5, 1/√5). We can plug this into the function to find that f(2/√5, 1/√5) = 3/5.
Therefore, the local maximum is (2/√5, 1/√5) with a value of 3/5, the local minimum is (-1/√2, 1/√2) and (1/√2, -1/√2) with a value of -1/4, and the absolute maximum is also (2/√5, 1/√5) with a value of 3/5, and the absolute minimum is on the border, which occurs at (0,1) and (0,-1) with a value of 0.
There are no critical points in the interior of the disk (not the border) that are not extremes or saddle points.
(i) Local extrema:
To find the local extrema, we first find the partial derivatives of f(x, y) with respect to x and y:
f_x = 2x + y
f_y = 2y + x
Set both partial derivatives equal to zero to find critical points:
2x + y = 0
2y + x = 0
Solving this system of equations, we find that the only critical point is (0, 0).
(ii) Absolute extrema:
To determine whether the critical point is an absolute maximum, minimum, or saddle point, we must examine the second partial derivatives:
f_xx = 2
f_yy = 2
f_xy = f_yx = 1
Compute the discriminant: D = f_xx * f_yy - (f_xy)^2 = 2 * 2 - 1^2 = 3
Since D > 0 and f_xx > 0, the point (0, 0) is an absolute minimum of the function.
(iii) Critical points and their classification:
The only critical point in the interior of the disk is (0, 0). As determined earlier, this point is an absolute minimum. No saddle points or other extrema are present within the interior of the disk.
To find any extrema on the boundary of the disk (x^2 + y^2 = 1), we use the method of Lagrange multipliers. However, as the boundary is not part of the domain specified in the question, we will not delve into that here.
Visit here to learn more about equation : https://brainly.com/question/29538993
#SPJ11
Find mZAEB
A
38°
B
66°
47°
859

Answers
Answer:
\( 85\degree \)
Step-by-step explanation:
By the property of intersecting chords inside a circle.
\( m\angle AEB=\frac{1}{2} (132\degree + 38\degree) \)
\( m\angle AEB=\frac{1}{2} \times 170\degree \)
\( m\angle AEB=85\degree \)
n traveling across flat land you notice a mountain directly in front of you. Its angle of elevation (to the peak) is 3.5 degrees. After you drove 13 miles closer, the angle of elevation is 9 degrees. What is the approximate height of the mountain?
Answers
The height of the mountain is 1.49 miles if in traveling across flat land you notice a mountain directly in front of you.
Given,
In the question:
Its angle of elevation (to the peak) is 3.5 degrees.
After you drove 13 miles closer, the angle of elevation is 9 degrees.
To find the approximate height of the mountain.
What is trigonometry?
Trigonometry is a branch of mathematics that deals with the relationship between the sides and angles of a right-angle triangle.
Now, According to the question:
It is given that:
In traveling across flat land you notice a mountain directly in front of you.
Applying tan ratio:
tan3.5 = h/(15+x)
Here h is the height of the mountain and x is the distance between the base of the mountain and to the second position of the car.
h = (15 + x) tan3.5
h = x tan9
(15 + x) tan3.5 = x tan9
x = 9.44
h = 9.44 tan9
h = 1.49 miles
Hence, the height of the mountain is 1.49 miles if in traveling across flat land you notice a mountain directly in front of you.
Learn more about Trigonometry at:
https://brainly.com/question/1969305
#SPJ4

how much is (((13x3)-3)/3)?
Answers
Answer: 12
Step-by-step explanation: 13*3=39
39-3=36
36/3=12✅
In a cookie mix, we find cinnamon cookies, raisin cookies, and pinwheel cookies in a ratio of 3 : 1 : 2. If a bag of the mix contains 26 pinwheel cookies, how many cookies in total are there? *
Answers
Answer:
39 : 13 : 26 or 78 cookies total
Step-by-step explanation:
if following the rule, divide the normal amount of cookies by the total
(26 divided by 2 = 13)
then multiply that 13 with the other two numbers and thats your answer
how much will money will u pay if a pair of 100 headphones have a 15% percent discount
Answers
Answer:
85
Step-by-step explanation:
out of 100 aka 100%, 15% is taken so subtract the too and you get 85
A washing machine in a laundromat breaks down an average of three times per
month. Using the Poisson probability distribution formula, find the probability that
during the next month this machine will have
a) exactly two breakdowns
b) at most one breakdown.
Answers
a) the probability of exactly two breakdowns in the next month is approximately 0.224 or 22.4%
b) the probability of at most one breakdown in the next month is approximately 0.199 or 19.9%.
To find the probability of the number of breakdowns in a month for the washing machine using the Poisson probability distribution, we need to know the average rate of breakdowns per month, which is given as three breakdowns.
The Poisson probability distribution formula is given by:
P(x; λ) = (\(e^{(-\lambda )\)* λ^x) / x!
Where:
P(x; λ) is the probability of x events occurring in a given interval,
λ is the average rate of events occurring in that interval,
e is the base of the natural logarithm, and
x! represents the factorial of x.
a) To find the probability of exactly two breakdowns, we substitute x = 2 and λ = 3 into the formula:
P(2; 3) = (\(e^{(-3)} * 3^2\)) / 2!
Calculating this, we get:
P(2; 3) ≈ 0.224
Therefore, the probability of exactly two breakdowns in the next month is approximately 0.224 or 22.4%.
b) To find the probability of at most one breakdown, we sum the probabilities of zero breakdowns and one breakdown:
P(0; 3) + P(1; 3)
Substituting x = 0 and λ = 3 into the formula for the first term:
P(0; 3) = (\(e^{(-3)} * 3^0)\) / 0! = \(e^{(-3)\)
Substituting x = 1 and λ = 3 into the formula for the second term:
P(1; 3) = (\(e^{(-3)} * 3^1\)) / 1! =\(3e^{(-3)\)
Calculating this sum, we get:
P(0; 3) + P(1; 3) = \(e^{(-3)} + 3e^{(-3)}\)
Approximating this value, we find:
P(0; 3) + P(1; 3) ≈ 0.199
Therefore, the probability of at most one breakdown in the next month is approximately 0.199 or 19.9%.
Using the Poisson probability distribution, we can determine the likelihood of different numbers of breakdowns occurring in a month for the washing machine in the laundromat.
For more such questions on probability visit:
https://brainly.com/question/251701
#SPJ8
(L5) Given: ΔABC with AC>AB;BD¯ is drawn so that AD¯≅AB¯Prove: m∠ABC>m∠C
Answers
Angle ABC is greater than angle C, as required. Given triangle ABC with AC greater than AB, and BD drawn such that AD is congruent to AB, we need to prove that angle ABC is greater than angle C.
To begin with, we can draw a diagram to visualize the situation. In the diagram, we see that BD is an altitude of triangle ABC, as well as a median since it divides the base AC into two equal parts. We also see that triangles ABD and ABC are congruent by the side-side-side (SSS) criterion, which means that angle ABD is equal to angle ABC.
Now, we can use this information to prove our statement. Since triangle ABD and triangle ABC are congruent, their corresponding angles are also equal. Therefore, we know that angle ABD is equal to angle ABC.
Next, we observe that angle ABD is a right angle, since BD is an altitude of triangle ABC. This means that angle ABC is the sum of angles ABD and CBD.
Since AD is congruent to AB, we also know that angles ABD and ADB are congruent. Therefore, angle CBD is greater than angle ADB.
Putting all of this together, we can conclude that angle ABC is greater than angle C, as required.
In summary, we have shown that given triangle ABC with AC greater than AB and BD drawn such that AD is congruent to AB, angle ABC is greater than angle C. This is because angles ABD and CBD add up to angle ABC, and angle CBD is greater than angle ADB.
learn more about congruence here: brainly.com/question/27922830
#SPJ11
What is the frequency?

Answers
Answer:
Its A
Step-by-step explanation:
If integer constraints are added to a linear programming model, then the optimal objective value will improve.
true or false?
Answers
Adding integer constraints to a linear programming model may or may not improve the optimal objective value.
When solving a linear programming problem, the standard approach is to relax the integer constraints and find an optimal solution in the continuous domain. This is known as linear programming (LP) relaxation. However, the optimal solution obtained from the LP relaxation may not satisfy the integer constraints. In such cases, if the integer constraints are added back to the problem, it becomes an integer programming (IP) problem.
The addition of integer constraints introduces discrete decisions into the problem, allowing for more precise control over the variables. In some cases, adding integer constraints can lead to a better optimal objective value because it forces the solution to select values that align with the discrete nature of the problem. This is especially true when the problem exhibits combinatorial or logical structures where discrete choices are crucial.
However, there are instances where adding integer constraints may not improve the optimal objective value. This can happen when the LP relaxation already provides an optimal solution that satisfies the problem's requirements. In such cases, the introduction of integer constraints may restrict the feasible solution space, making it harder to find a better solution.
In summary, while adding integer constraints to a linear programming model has the potential to improve the optimal objective value by incorporating discrete decisions, it is not guaranteed to do so. The impact of integer constraints depends on the problem structure and whether the LP relaxation already provides an optimal solution that meets the problem's criteria.
For more questions like Integer constraints click the link below:
https://brainly.com/question/32597572
#SPJ11
Avery has two books and a lunch box in his backpack Each book weighs 7/8 pound. The total weight in his backpack it 2 2/3 pounds. How much does Avery's lunch box weigh?
Answers
The weight of the Avery's lunch box using given weights is equal to 0.92 pounds (rounded to two decimal places).
Total weight of the backpack= 2 2/3 pounds
= 8/3 pounds
The weight of the each book =7/8 pounds.
Let x be the weight of the lunch box in pounds.
An equation that represents the total weight in Avery's backpack,
2(7/8) + x = 8/3
To solve for x, simplify and solve for x,
⇒14/8 + x = 8/3
Multiplying both sides by 24 the least common multiple of 8 and 3 to clear the fractions,
⇒42 + 24x = 64
Subtracting 42 from both sides,
⇒24x = 22
Dividing both sides by 24,
⇒x = 22/24
Simplifying the fraction,
⇒x = 11/12
= 0.92 pounds (rounded to two decimal places).
Therefore, the weight of the lunch box is equal to 0.92 pounds (rounded to two decimal places).
learn more about weight here
brainly.com/question/14315665
#SPJ4
What is the first step to be performed when computing Σ(X + 2)2?
a)Square each value
b)Add 2 points to each score
c)Sum the squared values
d)Sum the (X + 2) values
Answers
What is the first step to be performed when computing Σ(X + 2)2 option d) Sum the (X + 2) values. The first step in computing Σ(X + 2)2 is to perform the operation within the parentheses, which is adding 2 to each score. Once this is done, the resulting values of (X + 2) should be summed.
This is the explanation for the correct answer. Squaring each value (option a) or adding 2 points to each score (option b) are not the correct first steps in this calculation. Summing the squared values (option c) is also not the correct first step as the expression Σ(X + 2)2 requires summing the values before squaring them.
Therefore, the conclusion is that option d) is the correct first step in computing Σ(X + 2)2.
To know more about squared visit:
hhttps://brainly.com/question/14198272
#SPJ11
After restocking the vending machine, Dannie determined that 2 out of every 5 packages of candy were M&M’s. The vending machine sold 160 packages of candy last week. How many packages of M&M’s were sold?
Answers
Add.
(6x³ + 3x² − 2) + (x³ - 5x² − 3)
Express the answer in standard form. (Please and thank you)
Answers
Answer:
\(\\\sf7x^3 - 2x^2 - 5\)
Step-by-step explanation:
\(\\\sf(6x^3 + 3x^2 - 2) + (x^3 - 5x^2 - 3)\)
Remove parenthesis.
6x^3 + 3x^2 - 2 + x^3 - 5x^2 - 3
Rearrange:
6x^3 + x^3 + 3x^2 - 5x^2 - 2 - 3
Combine like terms to get:
7x^3 - 2x^2 - 5----------------------------------------
More on adding polynomials: https://brainly.com/question/30791478
Hope this helps! :)
Answer:
7x³ - 2x² - 5
Step-by-step explanation:
(6x³ + 3x² - 2) + (x³ - 5x² - 3)
Remove the round brackets.
= 6x³ + 3x² - 2 + x³ - 5x² - 3
Put like terms together.
= 6x³ + x³ + 3x² - 5x² - 2 - 3
Do the operations.
= 7x³ - 2x² - 5
____________
hope this helps!
What is the solution to this system of equations?
2x+y = 6
- - x - y = 2
0
0
(1, -1)
(0,8)
infinitely many solutions
no solution
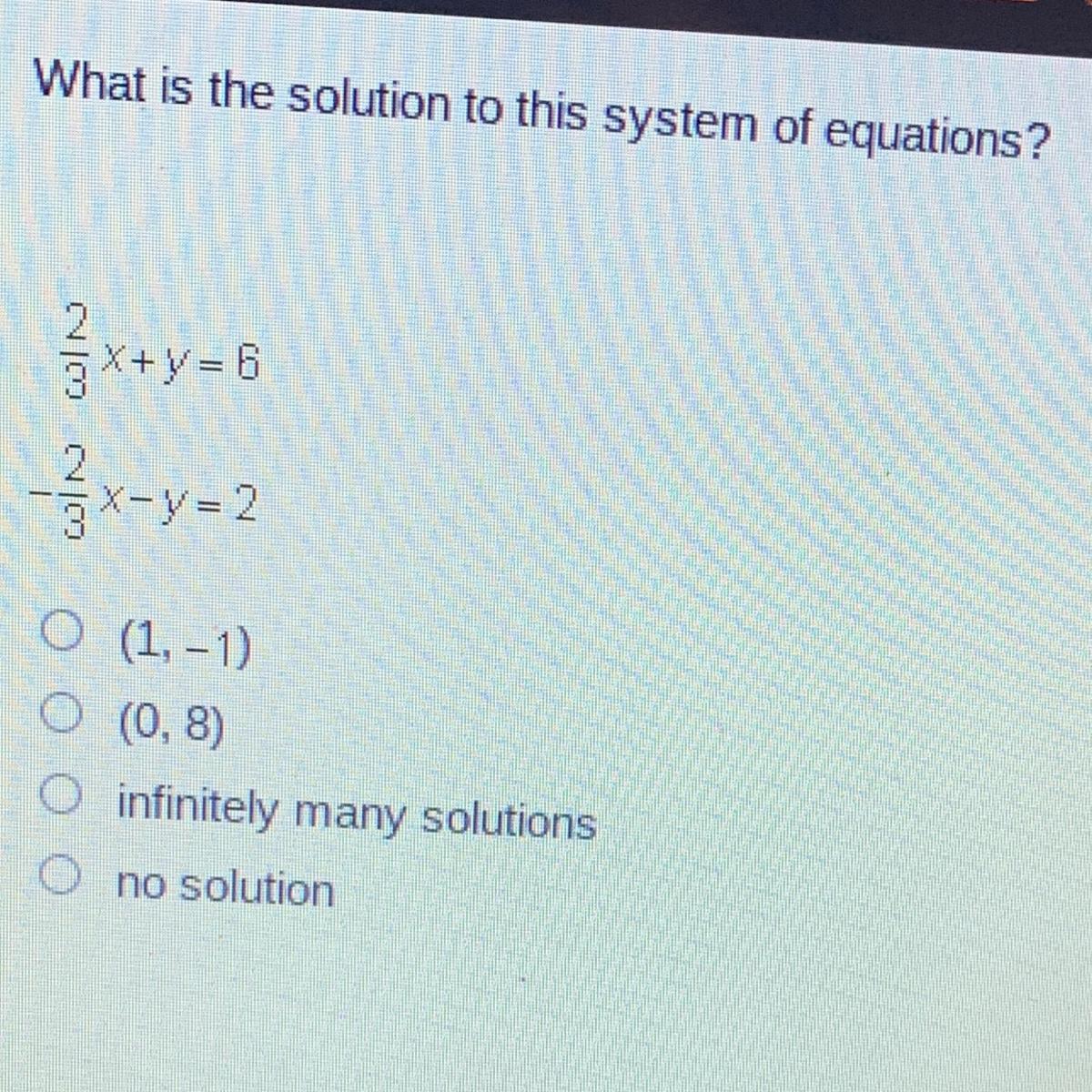
Answers
Answer:
Step-by-step explanation:
{ 2/3 x+y=6
+
{ -2/3x-y=2
= 0=6
Hence,no solution.
What is the word form for 6.005
Answers
Answer:
six and five thousands
Which is a valid conclusion that can be drawn from these statements?
If a quadrilateral is a rhombus, then it is a parallelogram.
If a quadrilateral is a parallelogram, then its opposite angles are congruent.
A. Opposite angles of a rhombus are congruent.
B.Opposite angles of a quadrilateral are congruent.
C. Every parallelogram is a rhombus.
D. Every quadrilateral is a rhombus.
Answers
Answer:
A. Opposite angles of a rhombus are congruent.
Step-by-step explanation: