The width of the large size is 9.9 cm and its height is 19.8 cm.
The width of the small size bottle is 4.5 cm.
hcm
h =
4.5 cm
Calculate the height of the small bottle.
19.8 cm
9.9 cm
+
cm
Answers
Answer and Explanation:
The height of the small bottle can be calculated using the ratio of the width of the large and small bottles.
Ratio of width = Large bottle width / Small bottle width
Ratio of width = 9.9 cm / 4.5 cm
Ratio of width = 2.2
Therefore, the height of the small bottle can be calculated by multiplying the ratio of width with the height of the large bottle.
Height of small bottle = Ratio of width x Height of large bottle
Height of small bottle = 2.2 x 19.8 cm
Height of small bottle = 43.56 cm
Related Questions
Algebraic Expression:
Add:
2a+3b
4a+7b
Answers
Answer:
6a + 10b
Step-by-step explanation:
(2a + 3b) + (4a + 7b) =
Drop the two sets of parentheses since they are unnecessary.
= 2a + 3b + 4a + 7b
Group like terms together.
= 2a + 4a + 3b + 7b
Add like terms.
= 6a + 10b
convert 2 Bigha into kattha
Answers
Answer:
To convert 2 Bigha into Kattha:
If 1 Bigha = 20 Kattha:
2 Bigha = 2 * 20 Kattha = 40 Kattha
If 1 Bigha = 16 Kattha:
2 Bigha = 2 * 16 Kattha = 32 Kattha
7. EFGH is a rectangle and IF = 8. Find EH.
Please answer #7 ASAP
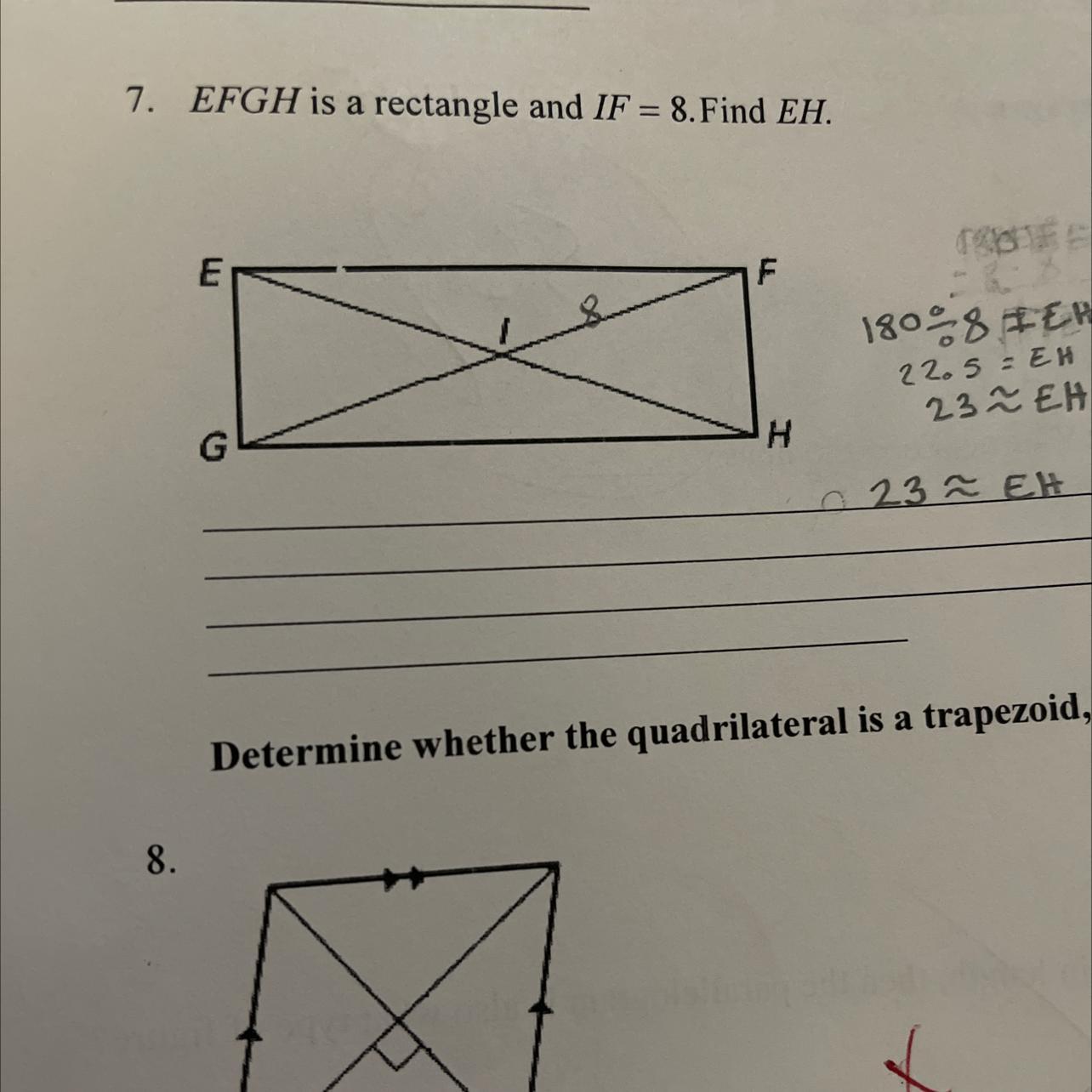
Answers
Answer:
16
Step-by-step explanation:
the diagonals intersect in the center...
you have collected information on the brand of phone owned by a 200 students. what is the variable type and level of measurement?
Answers
In the study of the brand of phone owned by 200 students, the variable type is a categorical variable with a nominal level of measurement.
A variable is a characteristic or attribute that can change or take on different values in a study or experiment. There are different types of variables in statistics, each with its own level of measurement.
In the case of the brand of phone owned by 200 students, the variable type is a categorical variable. This is because the brand of phone can be divided into distinct categories, such as Apple, Samsung, Huawei, etc.
The level of measurement for this variable is nominal. This means that the categories of phone brands are not ordered and do not have any inherent numerical meaning. They simply represent different, distinct categories, and the only relationship between them is that of membership to a specific category.
To know mare about variable refer here:
https://brainly.com/question/15740935#
#SPJ11
Help me out hdbshshshdhdhdhbdb

Answers
Answer:
Step-by-step explanation:
4 ( 3 ) - 6 = 6.
4 ( 7 ) - 6 = 22
4 ( 11 ) - 6 = 35
if you need 180g of flour for 24 cookies how much flour is needed for 200
Answers
Answer:
1500g
Step-by-step explanation:
First, divide 200 by 24 so that you can have a common ratio. This would get you 8.333... Then multiply 8.333... to 180. This would get you the answer of 1500 g. Hope this helps :)
The amount of flour to make 200 cookies will be 1500 grams.
What are ratio and proportion?A ratio is a group of sequentially ordered numbers a and b expressed as a/b, where b is never equal to zero. When two objects are equal, a statement is said to be proportional.
The definition of simplicity is making something simpler to achieve or grasp while also making it a little less difficult.
If you need 180g of flour for 24 cookies.
Let 'x' be the amount of flour. Then the ratio of the flour to cookies will be constant.
x / 200 = 180 / 24
x = 200 x 180 / 24
x = 1500 grams
The amount of flour to make 200 cookies will be 1500 grams.
More about the ratio and the proportion link is given below.
https://brainly.com/question/14335762
#SPJ5
You buy an 8-year $1,000 par value bond today that has a 6% yield and a 6% annual payment coupon. In 1 year promised yields have risen to 7%. Your 1-year holding-period return was
Answers
In one-year, the promised yields have risen to 7%, then the 1-year holding-period return was : (a) 0.61%.
The "Par-value" of the bond (face value) is = $1,000;
Coupon rate = 6% (annual payment coupon)
Yield at purchasing time is = 6%
Yield after 1 year = 7%
Step 1: Calculate the present value of the redeemable value:
We know that PVIF at 7% for 7 years is 0.623,
So, Present value of redeemable value = (Par value) × PVIF = $1,000 × 0.623 = $622.75,
Step 2: Calculate the present value of coupon payments:
Coupon payment = (Coupon rate)×(Par value) = 6% × $1,000 = $60,
We know that PVAF at 7% for 7 years is 5.389,
So, Present value of coupon payments = (Coupon payment) × (PVAF) = $60 × 5.389 = $323.36,
Step 3: Calculate the price of bond after 1 year:
Price of bond = Present value of redeemable value + Present value of coupon payments,
Substituting the values,
We get,
Price of bond = $622.75 + $323.36 = $946.11
Step 4: Calculate the 1-year holding-period return:
Holding return = (Price in next year + Coupon interest - Price in current year) / Price in current year,
Holding return = ($946.11 + $60 - $1,000) / $1,000
Holding return = $6.11 / $1,000
Holding return = 0.00611 = 0.61%.
Therefore, the correct option is (a).
Learn more about Bond here
https://brainly.com/question/31512988
#SPJ4
The given question is incomplete, the complete question is
You buy an 8-year $1,000 par value bond today that has a 6% yield and a 6% annual payment coupon. In 1 year promised yields have risen to 7%. Your 1-year holding-period return was
(a) 0.61%
(b) -5.39%
(c) 1.28%
(d) -3.25%
5. Let f(x,y) = 4 + root(x^2 + y^2). (a) Find the gradient of f at the point (-3,4). (b) Determine the equation of the tangent plane at the point (-3,4). (c) For what unit vectors u is the directional derivative (D_u)f = 0 at the point (-3, 4)?
Answers
c) the unit vectors u that satisfy (D_u)f = 0 at the point (-3, 4) are those that are orthogonal to the gradient vector ∇f(-3, 4),
(a) To find the gradient of f at the point (-3, 4), we need to find the partial derivatives of f with respect to x and y.
Partial derivative of f with respect to x:
∂f/∂x = (∂/∂x)(4 + \(sqrt(x^2 + y^2))\)
= (∂/∂x)(4 + \((x^2 + y^2)^{0.5})\)
= 0 + \((1/2)(x^2 + y^2)^{(-0.5)(2x)}\)
= \(x/(x^2 + y^2)^{0.5}\)
Partial derivative of f with respect to y:
∂f/∂y = (∂/∂y)(4 + \(sqrt(x^2 + y^2)\))
= (∂/∂y)(4 + \((x^2 + y^2)^{0.5})\)
= 0 +\((1/2)(x^2 + y^2)^{(-0.5)(2y)}\)
= \(y/(x^2 + y^2)^{0.5}\)
Therefore, the gradient of f at the point (-3, 4) is given by:
∇f(-3, 4) =\((x/(x^2 + y^2)^0.5, y/(x^2 + y^2)^0.5)\)
= (-3/5, 4/5)
(b) To determine the equation of the tangent plane at the point (-3, 4), we can use the point-normal form of the equation of a plane.
The normal vector to the plane is given by the gradient of f at the point (-3, 4), which we found in part (a): ∇f(-3, 4) = (-3/5, 4/5).
Using the point-normal form of the equation of a plane, the equation of the tangent plane at the point (-3, 4) is:
(-3/5)(x + 3) + (4/5)(y - 4) = 0
Simplifying the equation, we have:
-3x/5 - 9/5 + 4y/5 - 16/5 = 0
-3x/5 + 4y/5 - 25/5 = 0
-3x + 4y - 25 = 0
Therefore, the equation of the tangent plane at the point (-3, 4) is -3x + 4y - 25 = 0.
(c) For what unit vectors u is the directional derivative (D_u)f = 0 at the point (-3, 4)?
The directional derivative (D_u)f represents the rate of change of f in the direction of the unit vector u. When the directional derivative is zero, it means that the function is not changing in that direction.
At the point (-3, 4), the directional derivative (D_u)f is given by the dot product of the gradient of f at (-3, 4) and the unit vector u:
(D_u)f(-3, 4) = ∇f(-3, 4) · u = 0
For the dot product to be zero, the vectors ∇f(-3, 4) and u must be orthogonal (perpendicular) to each other. This means that the angle between them should be 90 degrees.
To know more about vectors visit:
brainly.com/question/24256726
#SPJ11
Solve the proportion v/84 =2/21
Answers
Answer:
there is no solution for this equation, Hope this helps! x <3
Step-by-step explanation:
v/84=2/21
We move all terms to the left:
v/84-(2/21)=0
We add all the numbers together, and all the variables
v/84-(+2/21)=0
We get rid of parentheses
v/84-2/21=0
We calculate fractions
There is no solution for this equation
Can someone answer this for e pleaseeeee

Answers
Answer: 220
Step-by-step explanation:
Derivations (20 marks): For each of the questions in this section provide a derivation. Other methods will receive no credit i. ∃x(Fx & Gx) ⊢ ∃xFx & ∃xGx (5 marks)
ii. ¬ 3x(Px v Qx) ⊢ Vx ¬ Px (5 marks) iii. ¬ Vx(Fx → Gx) v 3xFx (10 marks; Hint: To derive this theorem use RA.)
Answers
¬ Vx(Fx → Gx) v 3xFx ⊢ Fx → Gx [1-5, Modus Ponens]
i. ∃x(Fx & Gx) ⊢ ∃xFx & ∃xGx (5 marks)
Proof:
1. ∃x(Fx & Gx) [Premise]
2. Fx & Gx [∃-Elimination, 1]
3. ∃xFx [∃-Introduction, 2]
4. ∃xGx [∃-Introduction, 2]
5. ∃xFx & ∃xGx [Conjunction Introduction, 3 and 4]
6. ∃x(Fx & Gx) ⊢ ∃xFx & ∃xGx [1-5, Modus Ponens]
ii. ¬ 3x(Px v Qx) ⊢ Vx ¬ Px (5 marks)
Proof:
1. ¬ 3x(Px v Qx) [Premise]
2. ¬ Px v ¬ Qx [DeMorgan’s Law, 1]
3. Vx ¬ Px [∀-Introduction, 2]
4. ¬ 3x(Px v Qx) ⊢ Vx ¬ Px [1-3, Modus Ponens]
iii. ¬ Vx(Fx → Gx) v 3xFx (10 marks; Hint: To derive this theorem use RA.)
Proof:
1. ¬ Vx(Fx → Gx) v 3xFx [Premise]
2. (¬ Vx(Fx → Gx) v 3xFx) → (¬ Vx(Fx → Gx) v Fx) [Implication Introduction]
3. ¬ Vx(Fx → Gx) v Fx [Resolution, 1, 2]
4. (¬ Vx(Fx → Gx) v Fx) → (Fx → Gx) [Implication Introduction]
5. Fx → Gx [Resolution, 3, 4]
6. ¬ Vx(Fx → Gx) v 3xFx ⊢ Fx → Gx [1-5, Modus Ponens]
Learn more about Derivations
brainly.com/question/30365299
#SPJ11
In 1787 the French scientist Jacques Charles observed that when he plotted the graph of volume of a fixed amount of air versus the temperature of the air, the points lay along a straight line. Therefore, he concluded that volume of a gas varies linearly with temperature. Suppose that at 27º C a certain amount of air occupies a volume of 500 cm3. When it is warmed to 90º C, it occupies 605 cm3.
a) Write the particular equation in slope-intercept form expressing volume in terms of temperature.
b) Predict the volume at 60º C.
c) The process of predicting a value between two data points is called “interpolation”.
What is the origin of the word?
d) Predict the volume at 300º C.
e) The process of predicting a value beyond any given data points is called
“extrapolation”. What is the origin of this word?
f) Extrapolate your mathematical model back to the point where the volume is zero.
That is, find the temperature-intercept.
g) What is the special name given to the temperature in part f)?
Answers
The relationship between the volume, V, and temperature, T, of a given mass of gas, found by the French scientist Jacques Charles, gives;
a) The slope–intercept form of the equation that expresses the volume in terms of the temperature of the gas is; \( \displaystyle{ V = 1. \bar 6 \cdot T + 455}\)
b) The volume at 60 °C is 555 cm³
c) Interpolation originates from the verb interpolare
d) The temperature at 300 °Cis 955 cm³
e) Extrapolation originates from 'extra' (meaning outside) and the shortened form of Interpolation
f) The temperature–intercept is -273 °C
g) The special name is the absolute zero temperature
What is Charles law for gases?Charles law states that the volume of a given mass of gas is directly proportional to its temperature given in Kelvin.
Mathematically, Charles Law states that; V = K•T
Where;
V = The volume of the gas
T = The gas temperature
K = The proportionality constant
The volume occupied by the gas at 27 °C = 500 cm³
The volume occupied at 90 °C = 605 cm³
a) To write the equation in slope–intercept form, we have;
\( \displaystyle{ Slope = \frac{605 - 500}{90 - 27} =1. \bar{6} =1. \bar{6}}\)
The equation of the line in point and slope form is therefore;
Point–slope form; \( \displaystyle{ V - 500 = 1. \bar{6} \times (T - 27) }\)
\( \displaystyle{ V = 1. \bar{6} \cdot T -45 + 500 = 1. \bar{6} \cdot T + 455}\)
The equation in slope–intercept form of expressing the volume, V, in terms of the temperature, T, is therefore;
Volume equation; \( \displaystyle{ V = 1. \bar{6} \cdot T + 455}\)
b) The volume at 60 °C is given from the equation that gives the volume, V, in terms of time, T as follows;
\( \displaystyle{ V(T) = 1. \bar{6} \cdot T + 455}\)
When T = 60 °C
\( \displaystyle{ V(60) = 1. \bar{6} \times 60 + 455=555}\)
The volume occupied by the gas at 60 °C is 555 cm³c) The word interpolate originated from the Latin word interpolare which means to alter or refurbish
d) The volume occupied by the gas at 300 °C is given by the function for the volume, V, in terms of temperature, T, equation as follows;
When T = 300 °C
\( \displaystyle{ V(300) = 1. \bar{6} \times 300 + 455 = 955}\)
The volume of the gas at 300 °C is 955 cm³e) Extrapolation originate from the word 'extra' which refers to the outside of an area. Extra is combined with a short form of interpolate to give the word, extrapolation
f) When the volume is zero, the volume function equation can be used to find the temperature as follows;
Volume function; \( \displaystyle{ V = 1. \bar{6} \cdot T + 455}\)
When V = 0
\( \displaystyle{ V = 0 =1. \bar{6} \cdot T + 455}\)
\( \displaystyle{ -455 = 1. \bar{6} \cdot T }\)
\( \displaystyle{T = \frac{3 \times (-455)}{5}= -273 }\)
The temperature at which the volume of the gas is zero is -273 °Cg) The special name given to -273 °C of the gas is the absolute zero temperature.
Learn more about Charles law for gases here:
https://brainly.com/question/16927784
#SPJ1
7 divided by 55 but every step must be shown, thank you
Answers
Step-by-step explanation:
how many positions after the decimal point ?
7 ÷ 55 = 0.12727...
7 remainder, we ran out of digits before the decimal point
70 (when there are no more digits, we simply pull 0s)
15 remainder
150
40 remainder
400
15 remainder
150
40 remainder
400
15 remainder
... (that loop now continues forever)
find the value of x
(7x - 12) 114

Answers
Answer:
(7x-12)=-5
-5x÷-5 114÷-5=
x=29
\((7x - 12) + 114 = 180\)
Reason: The cointerior angles equal 180°
Collecting like terms:
\(7x + 102 = 180 \\ 7x = 180 - 102\)
\(7x = 78\)
Divide both sides of the equation by the coefficient of 7x which is 7.
\( \frac{7x}{7} = \frac{78}{7} \)
\(x = \frac{78}{7} = \\ = 11.14\)
( The decimal answer is not necessary except if asked for)
I hope this helps.Someone pls help this is an easy question if u know what ur doing !!
Bea has decided to use the elimination method to solve the system of equations as
shown below.
3x - y = 23
2 + 2y = 10
Which of the following statements could be Bea's first step.
on
O Multiply the top equation by 2. then add the equations together.
O Multiply the top equation by-2. then add the equations together,
O Multiply the bottom equation by 3, then add the equations together,
O Multiply the top equation by 2 and the bottom equation by 3, then add the equations together

Answers
I think the first option is the correct one.
for elimination you'd need to multiply one of the equations by a number in order to cancel out the other equation.
There are several ways to solve a system of equations, one of them is the elimination method.
The statement that can represent Bea's first step is (a) multiply the top equation by 2, then add the equations together.
The system of equation is given as:
\(3x - y = 23\)
\(x + 2y = 10\)
To eliminate y, we start by multiplying the top equation by 2
\(3x - y = 23\)
This gives
\(2(3x - y = 23)\)
\(6x - 2y =46\)
Add this equation to the bottom equation
\(6x + x - 2y + 2y =46 + 10\)
\(7x =56\)
Notice that the variable y has been eliminated.
Hence, the possible first step is statement (a)
Read more about system of equations at:
https://brainly.com/question/14323743
Jamal has a drawer containing 6 green socks, 18 purple socks, and 12 orange socks. After adding more purple socks, Jamal noticed that there is now a 60% chance that a sock randomly selected from the drawer is purple. How many purple socks did Jamal add?
A 6
B 9
C 12
D 18
E 24
Answers
Answer:
B 9
Step-by-step explanation:
We have 6 green socks, 18 purple socks, and 12 orange socks.
Adding more purple sock means 6 green socks, 18+x purple socks, and 12 orange socks.
We have a probability of 60% of getting a purple sock.
P( purple) = number of purple socks / total
.60 = (18+x) / (6+18+x+12)
.60 = (18+x) / (36+x)
Multiply each side by 36+x
21.6 +.6x = 18+x
Subtract 18 from each side
3.6x +.6x = x
Subtract .6x from each side
3.6x = .4x
Divide each side by .4
9 =x
Jamal added 9 purple socks
if two measures have a high positive correlation, and a person has a low score on one measure, her score on the other measure is most likely to be
Answers
The answer is low using correlation.
What is correlation?
The terms "co" and "relation" are combined to form the word "correlation." Correlation is the relationship between any set of data when taken as a whole because the term "co" signifies together.
The correlation coefficient, which in statistics is a number between -1 and +1, measures the linear dependency of the collection of data.
It cannot capture nonlinear correlations between two variables and only assesses the magnitude and direction of the linear link between the two variables.
The difference between dependent and independent variables is not possible.
In the question, it is given that there is a high positive correlation between x and y, which means for every increase in x there is a corresponding increase in y
So if x is having low score, than y is also having low score
Hence the answer is low.
Learn more about arithmetic, by the following link.
https://brainly.com/question/4219149
#SPJ4
Write the equation of the graph shown below in factored form.
Option A: f(x) = (x-2)^2(x+1)(x-3)
Option B: f(x) = (x+2)^2(x-1)(x+3)
Option C: f(x) = (x+2)^2(x+1)(x+3)
Option D: f(x) = (x-2)^2(x-1)(x-3)
Please show and explain all work.

Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
The Correct choice is Option A

Select the TRUE statements: a A sufficiently large sample size for the central limit theorem is greater than 30 b The variability of sampling distribution of the mean (X-bar) is less than the variability of the individual observations (X) c A sufficiently large sample size for the central limit theorem is greater than 50 d The variability of sampling distribution of the mean (X-bar) is more than the variability of the individual observations (X)
Answers
The true statements are:
b. The variability of the sampling distribution of the mean (\(\overline x\)) is less than the variability of the individual observations (x)
a. A sufficiently large sample size for the central limit theorem is greater than 30.
The central limit theorem:The CLT states that if a sample is drawn randomly from any population, the distribution of sample means will approach a normal distribution, regardless of the shape of the population distribution, as the sample size increases.
This means that for large enough sample sizes, the mean and standard deviation of the sample mean can be estimated using a normal distribution.
Let's check each option as follows
Statement c is false because a sample size of 30 or greater is often considered sufficiently large for the central limit theorem.
Statement d is false because the variability of the sampling distribution of the mean decreases as the sample size increases, which is why the central limit theorem is useful.
Therefore,
The true statements are:
b. The variability of the sampling distribution of the mean (X-bar) is less than the variability of the individual observations (X)
a. A sufficiently large sample size for the central limit theorem is greater than 30.
Learn more about Central limit theorem at
https://brainly.com/question/18403552
#SPJ4
How many solutions does this equation have?2(x+2)+3=2(x+1)+1
Answers
Answer:
no solutions
Step-by-step explanation:
2(x+2)+3=2(x+1)+1
Distribute...
2x+4+3=2x+2+1
combine like terms...
2x+7=2x+3
rearange
7=-2x+2x+3
Combine like terms
7=3
there fore this equation has no solution the -2x and the +2x cancel each other out.
writing 5a2b − 13ab 7a3 − 4b in polynomial decending order
Answers
For the given polynomial 5a²b-13ab+7a³-4b, the descending order is 7a³+5a²b-13ab-4b.
What is polynomial?Polynomials are sums of terms of the form k⋅xⁿ, where k is any number and n is a positive integer. For example, 3x+2x-5 is a polynomial. Polynomials are introduced. This video defines words such as degree, standard form, monomial, binomial, and trinomial. A polynomial is an expression made up of variables, constants, and exponents that are combined using mathematical operations like addition, subtraction, multiplication, and division (No division operation by a variable).
Here,
The given polynomial is,
=5a²b-13ab+7a³-4b
The descending order,
=7a³+5a²b-13ab-4b
The descending order of polynomial is 7a³+5a²b-13ab-4b for the given polynomial 5a²b-13ab+7a³-4b.
To know more about polynomial,
https://brainly.com/question/11536910
#SPJ4
HEY CAN ANYONE PLS ANSWER DIS MATH PROBLEM!!!

Answers
Step-by-step explanation:
Number of triangles Perimeter
1 5*2 + 3*1 = 13
2 5*2 + 3*2 = 16
3 5*2 + 3*3 = 19
Points
(1, 13), (2, 16), (3, 19)The graph is attached

If f(x)=1/3x+7 and g(x)=-2x-5, find f(g(-7))
Please help.
Answers
Answer:
\(f(g(-7))=10\)
Step-by-step explanation:
We have the two functions:
\(\displaystyle f(x)=\frac{1}{3}x+7\text{ and } g(x)=-2x-5\)
And we want to find:
\(f(g(-7))\)
So, we will first find g(-7). We know that:
\(g(x)=-2x-5\)
Then by substitution:
\(g(-7)=-2(-7)-5\)
Evaluate. Multiply:
\(g(-7)=14-5=9\)
Therefore, we can rewrite our expression as:
\(f(g(-7))=f(9)\)
Since we know that:
\(\displaystyle f(x)=\frac{1}{3}x+7\)
By substitution:
\(\displaystyle f(9)=\frac{1}{3}(9)+7\)
Evaluate:
\(f(9)=3+7=10\)
Therefore:
\(f(g(-7))=10\)
Answer:
\(\boxed {\boxed {\sf f(g(-7))= 10}}\)
Step-by-step explanation:
We are asked to find f(g(-7)) given these 2 functions:
\(f(x)=\frac{1}{3}x+7\)\(g(x)= -2x-5\)We must work from the inside out, so first find g(-7).
1. g(-7)
The function for g is:
\(g(x)= -2x-5\)
Since we want to find g(-7), plug -7 in for x.
\(g(-7)= -2(-7)-5\)
Solve according the PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.
Multiply -2 and -7.
\(g(-7)=14-5\)
Subtract 5 from 14.
\(g(-7)=9\)
2. f(9)
Refer back to the original problem: f(g(-7))
Since we found that g(-7) is 9, we can substitute 9 in: f(9)
The function for f is:
\(f(x)= \frac{1}{3} x+7\)
Plug 9 in for x.
\(f(9)=\frac{1}{3}(9)+7\)
Solve according to PEMDAS and multiply 1/3 and 9.
\(f(9)=3+7\)
Add 3 and 7.
\(f(9)=10\)
f(g(-7) is equal to 10
Can someone help me?

Answers
Answer:
1 feet
Step-by-step explanation:
15-14
You have prizes to reveall go to your ga
seventh grade
z. 1 scale drawings: word problems 84h
)) steven made a scale drawing of a theater. the stage is 5 inches wide in the drawing. the
actual stage is 20 feet wide. what is the scale of the drawing?
) 1 inch :
feet
Answers
As per given data, the scale of the drawing is 4 feet wide.
Which direction is width?Length, width, and height are measurements that allow us to indicate the volume of geometric bodies. The length (20 cm) and the width (10 cm) correspond to the horizontal dimension. On the other hand, the height (15 cm) refers to the vertical dimension.
How wide is feet?A wide width is 1/4” wider than a medium width and an extra wide width is 1/2” wider than a medium width. People with foot swelling or edema may benefit from additionally measuring their instep girth, which will help them choose the appropriate shoe width.
In real life, width of stage = 20 feet
In drawing, width of stage = 5 inches
To find the actual scale of the drawing,
Based on the given conditions, formulate:: width in real life/width in drawing
= 20/5
Cross out the common factor: 4
To learn more about measurements visit:
brainly.com/question/4725561
#SPJ4
Persevere with Problems The table shows the highway fuel economy of various popular vehicles.

Answers
The mean absolute deviation of highway fuel economy of various popular vehicles is 4.9
How to find mean absolute deviation?Find the mean of the data set
= (38 + 48 + 25 + 35 + 33 + 37 + 32 + 34 + 23 + 30) / 10
= 335 / 10
= 33.5
Mean deviation of each set;
38 - 33.5 = 4.5
48 - 33.5 =14.5
25 - 33.5 = -8.5
35 - 33.5 = 1.5
33 - 33 .5 = -0.5
37 - 33.5 = 3.5
32 - 33.5 = -1.5
34 - 33.5 = 0.5
23 - 33.5 = -10.5
30 - 33.5 = -3.5
Absolute deviation of each value
|4.5| = 4.5
|14.5| = 14.5
|8.5| = 8.5
|1.5| = 1.5
|-0.5| = 0.5
|3.5| = 3.5
|-1.5| = 1.5
|0.5| = 0.5
|-10.5| = 10.5
|-3.5| = 3.5
Total absolute deviation = 4.5 + 14.5 + 8.5 + 1.5 + 0.5 + 3.5 + 1.5 + 0.5 + 10.5 + 3.5
= 49
Mean absolute deviation = Total absolute deviation / mean
= 49/10
= 4.9
Learn more about mean absolute deviation:
https://brainly.com/question/3998118
#SPJ1
The following angles are given in degrees, arcminutes, and arcseconds. Rewrite them in degrees and decimal fractions of degrees.A. 2 degrees 18 ′ 36 ′′B. 36 ′ 18 ′′C. 7 degrees 59′ 59′′D. 1′E. 1′′
Answers
On solving the provided question, we can say that 1 degree = 3600 arc seconds and 1 degree = 60 arc minutes.
what is degrees ?A 160 degree angle is measured in arc minutes, often known as arcmin, arcmin, arcmin, or arc minutes (represented by the sign '). One minute is equal to 121600 revolutions, or one degree, hence one degree equals 1360 revolutions (or one complete revolution). A degree, also known as a complete angle of arc, angle of arc, or angle of arc, is a unit of measurement for plane angles in which a full rotation equals 360 degrees. A degree is sometimes referred to as an arc degree if it has an arc of 60 minutes. Since there are 360 degrees in a circle, an arc's angles make up 1/360 of its circumference.
1 degree = 3600 arc seconds
1 degree = 60 arc minutes
A. 2 degree 18'36 = 2 + 18/60 + 36 / 2600 = 231 / 100 degree
B. 36 ′ 18 ′′ = 36/60 + 18/2600 = 121 / 200 degree
C. 7 degrees 59′ 59′′ = 7 + 59 / 60 + 59 / 3600 = 28799 / 3600 degree
D. 1' = 1/60 degree
F. 1" = 1/3600 degree
To know more about degree visit:
https://brainly.com/question/364572
#SPJ4
a croissant shop has plain croissants, cherry croissants, chocolate croissants, almond croissants, apple croissants, and broccoli croissants. how many ways are there to choose ) two dozen croissants with at least two of each kind?
Answers
There are 6188 ways are there to choose two dozen croissants with at least two of each kind.
A combination is the combination of two or more distinct things. Although it is not necessary to combine things in pairs, the term "combining" comes from the Latin word for "joining together two by two."Combination repetition is permitted.
There are six different varieties of croissants (n = 6), and we must select two dozen croissants (r = 12) with at least two of each type.
In combination, The order does not matter and repetition is allowed.
thus, according to combination,
\(C( n+ r - 1,r) = \frac{(n + r - 1 )!}{r! (n-1)!} \\\\C( 6+ 12 - 1,12) = \frac{(6 + 12 - 1 )!}{12! (6-1)!} \\\\ = \frac{17!}{12!5!} \\= 6188\)
thus, there are 6188 ways possible to choose two dozen croissants with at least two of each kind.
Know more about combination here: https://brainly.com/question/11732255
#SPJ4
Julio says, If you subtract 18 from my number and multiply the difference by -5 , the result is-80 . What is s number?
Answers
Answer:
34 is your answer
Step-by-step explanation:
34-18=16
16(-5)=-80
Answer:
\(s=34\)
Step-by-step explanation:
Set up an equation using the given information:
our number is represented by ssubtract 18 from smultiply the difference by -5result is -80"Multiply the difference" suggests that the subtraction should be done first. Following PEMDAS, in order to get subtraction done first, it would need to be in parentheses:
\((s-18)\)
Then you would multiply that difference by -5:
\(-5*(s-18)\)
Now set the expression as equal to -80:
\(-80=-5(s-18)\)
Now you can solve for s. Use the distributive property:
\(-80=-5(s)-5(-18)\\\\-80=-5s+90\)
Isolate the variable s. Subtract 90 from both sides:
\(-80-90=-5s+90-90\\\\-170=-5s\)
Divide both sides by -5:
\(\frac{-170}{-5}=\frac{-5s}{-5} \\\\34=s\)
Your number is 34.
:Done
Check answer:
Insert the value of s into the equation to determine if true:
\(-80=-5(34-18)\\\\-80=-5(16)\\\\-80=-80\)
This is true, so the value of s is correct.
a study has two groups of subjects who receive different treatments but take the same posttreatment t test. what analytic statistic will be appropriate?
Answers
To compare the posttreatment t-test scores of two groups of subjects who received different treatments, the appropriate analytic statistic would be a two-sample t-test. An independent samples t-test would be appropriate for analyzing the data.
This test is used to determine whether there is a statistically significant difference between the means of two independent groups. The two-sample t-test assumes that the samples are independent, normally distributed, and have equal variances.
It calculates a t-statistic, which measures the difference between the sample means relative to the variation within the groups, and compares it to a t-distribution to determine the probability of observing such a difference by chance.If the probability is lower than a predetermined significance level (usually 0.05), then we reject the null hypothesis that the two group means are equal and conclude that there is a statistically significant difference between the treatments.
To learn more about “statistics” refer to the https://brainly.com/question/15525560
#SPJ11