This has 2 parts - The first one is the easy part, the
second parts presents a challenge. You must show
your strategy and calculations to receive full credit.
Write your answer as whole numbers in hours and
in minutes. (Example: 35.25 = 35 hours and 15
minutes (NOTE: every 0.1 hour = 6 minutes))
Part 1: 2 airplanes left the same airport at the same
time. One is traveling at 422 mph straight east, the
other is traveling 384 mph straight west.
How long will it take before they are 6045 miles
apart?
Part 2: 2 airplanes left the same airport at the same
time. One is traveling at 422 mph straight NORTH,
the other is traveling 384 mph straight WEST.
How long will it take before they are 1997 miles
apart?
Answers
Answer:
Step-by-step explanation:
Part 1)
add their velocities
422+384= 806
now divide 6045 by 806 = 7.5 or 7 hours 30 minutes
7:30 = t hours:minutes
Part 2)
For this part we will need to employ Pythagoras theorem. we need the hypotenuse to be 1,997
so, when will plane traveling N , and plane traveling W be that far (1997)?
or
when does \(1997^{2}\) = \(N^{2}\) + \(W^{2}\)
then we're also given that N = 422*t
and that W = 384 * t
so now our formula looks like
\(1997^{2}\) = \((422*t)^{2}\) + \((384*t)^{2}\)
rewrite this so it's making clear math sense
\(1997^{2}\) = \(422^{2}\) * \(t^{2}\) + \(384^{2}\) * \(t^{2}\)
now pull out the \(t^{2}\)
\(1997^{2}\) = ( \(422^{2}\) + \(384^{2}\) ) * \(t^{2}\)
now simplify some
3988009 = (178084 + 147456 ) * \(t^{2}\)
now divide the left side by the numbers on the right
3988009 / (178084 + 147456 ) = \(t^{2}\)
12.12044234 = \(t^{2}\)
\(\sqrt{12.25044234}\) = t
3.500063191 = t
so at 3 and a half hours, the planes will be 1997 miles apart
3:30 = t
Related Questions
Help me please i am stuck

Answers
To find the length of x, add the opposite side. The opposite side is made up of:
4cm + 7 cm = 11cm
You may need to use the appropriate appendix table or technology to answer this question.
A population has a mean of 800 and a standard deviation of 200. Suppose a sample of size 400 is selected and
x
is used to estimate μ. (Round your answers to four decimal places.)
(a)____
What is the probability that the sample mean will be within ±5 of the population mean?
(b)___
What is the probability that the sample mean will be within ±10 of the population mean?
Answers
a. The probability that the sample mean will be within ±5 of the population mean is the area under the normal curve between these two z-scores. b. The lower bound z-score is (-10 - 0) / 10 = -1, and the upper bound z-score is (10 - 0) / 10 = 1. We can use the same normal distribution table or technology to find the probability associated with these z-scores.
(a) To find the probability that the sample mean will be within ±5 of the population mean, we can use the Central Limit Theorem (CLT) and the properties of a normal distribution.
The sample mean, is an unbiased estimator of the population mean, μ. According to the CLT, the distribution of sample means approaches a normal distribution with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
= 200 / √400
= 200 / 20
= 10
To find the probability that the sample mean will be within ±5 of the population mean, we can standardize the interval using the z-score:
For the lower bound (-5), the z-score is (-5 - 0) / 10 = -0.5.
For the upper bound (+5), the z-score is (5 - 0) / 10 = 0.5.
We can now use a standard normal distribution table or technology (such as a calculator or statistical software) to find the probability associated with the z-scores -0.5 and 0.5. The probability that the sample mean will be within ±5 of the population mean is the area under the normal curve between these two z-scores.
(b) To find the probability that the sample mean will be within ±10 of the population mean, we follow the same steps as in part (a).
The lower bound z-score is (-10 - 0) / 10 = -1, and the upper bound z-score is (10 - 0) / 10 = 1. We can use the same normal distribution table or technology to find the probability associated with these z-scores.
Note: Since the question mentions rounding answers to four decimal places, please use the appropriate table or technology to obtain the precise probabilities for parts (a) and (b).
Learn more about probability here
https://brainly.com/question/25839839
#SPJ11
1) f(t)=t2+sin(2t)+2cos(2t)+e−tsin(3t) You must solve the problem manually. You can only use MATLAB or other computer tools to verify your solution.
Answers
The solution to the integral of f(t) = t^2 + sin(2t) + 2cos(2t) + e^(-t)sin(3t) is:
F(t) = (1/3)t^3 - (1/2)cos(2t) + (1/2)sin(2t) - 4e^(-t)cos(3t) + C
where F(t) represents the antiderivative or the indefinite integral of f(t).
To find the solution for the function f(t) = t^2 + sin(2t) + 2cos(2t) + e^(-t)sin(3t) manually, we need to analyze each term separately.
Term: t^2
The integral of t^2 with respect to t is (1/3)t^3.
Term: sin(2t)
The integral of sin(2t) with respect to t is -(1/2)cos(2t).
Term: 2cos(2t)
The integral of 2cos(2t) with respect to t is (1/2)sin(2t).
Term: e^(-t)sin(3t)
To integrate this term, we can use integration by parts. Let's define u = e^(-t) and dv = sin(3t) dt.
Taking the derivatives and integrals:
du = -e^(-t) dt
v = -(1/3)cos(3t)
Using the integration by parts formula:
∫ u dv = uv - ∫ v du
∫ e^(-t)sin(3t) dt = -e^(-t)(1/3)cos(3t) - ∫ -(1/3)cos(3t)(-e^(-t)) dt
= -e^(-t)(1/3)cos(3t) + (1/3)∫ cos(3t)e^(-t) dt
We can apply integration by parts again to the remaining integral:
Let u = cos(3t) and
dv = e^(-t) dt.
Taking the derivatives and integrals:
du = -3sin(3t) dt
v = -e^(-t)
Using the integration by parts formula again:
∫ cos(3t)e^(-t) dt = -e^(-t)cos(3t) - ∫ (-e^(-t))(-3sin(3t)) dt
= -e^(-t)cos(3t) + 3∫ e^(-t)sin(3t) dt
Substituting the value we found for the previous integral:
∫ e^(-t)sin(3t) dt = -e^(-t)(1/3)cos(3t) + (1/3)(-e^(-t)cos(3t) + 3∫ e^(-t)sin(3t) dt)
Now we can solve for the integral:
∫ e^(-t)sin(3t) dt = (-e^(-t)(1/3)cos(3t) - (1/3)e^(-t)cos(3t))/(1 - 1/3)
= -3e^(-t)(1/3)cos(3t) - 3e^(-t)cos(3t)
= -e^(-t)cos(3t) - 3e^(-t)cos(3t)
= -4e^(-t)cos(3t)
Now we can put all the terms together:
∫ f(t) dt = (1/3)t^3 - (1/2)cos(2t) + (1/2)sin(2t) - 4e^(-t)cos(3t)
Let's continue with the expression for the integral:
∫ f(t) dt = (1/3)t^3 - (1/2)cos(2t) + (1/2)sin(2t) - 4e^(-t)cos(3t) + C
where C is the constant of integration.
So, the solution to the integral of f(t) = t^2 + sin(2t) + 2cos(2t) + e^(-t)sin(3t) is:
F(t) = (1/3)t^3 - (1/2)cos(2t) + (1/2)sin(2t) - 4e^(-t)cos(3t) + C
where F(t) represents the antiderivative or the indefinite integral of f(t).
To know more about integral visit
https://brainly.com/question/31433890
#SPJ11
the greek letter used to represent the probability of a type i error is alpha (α). true or false
Answers
True, the Greek letter used to represent the probability of a Type I error is alpha ().
The Greek letter alpha (α) is indeed used in statistics, but it represents the level of significance chosen for a statistical test. The level of significance is the probability of rejecting the null hypothesis when it is actually true. The probability of making a Type I error (rejecting the null hypothesis when it is true) is equal to the level of significance (α) chosen for the test.
Therefore, alpha is not used to represent the probability of a Type I error directly, but it is related to it. The probability of a Type I error depends on the chosen level of significance and the specific hypothesis test being conducted.
To know more about probability visit:-
https://brainly.com/question/30034780
#SPJ11
True. The Greek letter used to represent the probability of a Type I error is alpha
This is a statement and not a question. However, if you are asking whether the statement "the Greek letter used to represent the probability of a type i error is alpha (α)" is true or false, the answer is that it is partially true. While the Greek letter α is commonly used to represent the significance level (or the probability of a Type I error) in hypothesis testing, it is not the only letter that can be used.
Other letters such as β and γ may also be used in certain contexts. So the complete answer would be a long answer that explains the partial truth of the statement.
To know more about probability visit:-
https://brainly.com/question/32004014
#SPJ11
What are the properties of the circumcenter of a triangle quizlet?
Answers
For different types of triangle, The circumcenter has different properties. The properties varies for acute, obtuse and right angle triangles.
What do you mean by a triangle?A polygon with three edges and three vertices is called a triangle. It is one of the fundamental geometric shapes.
What do you mean by circumcenter of triangle?The spot where the three perpendicular bisectors of a triangle's sides meet and which is equally spaced from the triangle's three vertices.
Properties of circumcenter of triangle are:
In an acute-angled triangle, circumcenter lies inside the triangle. In an obtuse-angled triangle, it lies outside of the triangle. Circumcenter lies at the midpoint of the hypotenuse side of a right-angled triangle.To learn more about circumcenter visit:
https://brainly.com/question/16276899
#SPJ4
The thin‑layer chromatography (TLC) plate shown was developed with 20% ethyl acetate in hexanes. (4)
Suppose the plate had instead been developed with 5% ethyl acetate in hexanes. Determine whether each plate is a possible result of the adjusted development process
Answers
The solvent characteristics of the formed plate would probably change from those of the unaltered plate development process if it had been developed with 5% ethyl acetate in hexanes.
Hexanes are nonpolar while ethyl acetate is polar, therefore mixing the two together would probably produce a more polar solvent solution.This might alter the chemicals' solubility and movement on the plate, possibly resulting in various separation patterns and band intensities.Additionally, it's feasible that the 5% ethyl acetate in hexane solution will improve the separation of the chemicals on the plate since the solvents' polar and nonpolar characteristics.
May combine to do so.However, it would rely on the different kinds of compounds on the plate and each one's unique solubility characteristics.
Conclusion: The 5% ethyl acetate in hexanes produced plate may have varied solvent characteristics, which may result in different separation patterns and band intensities, but it is impossible to know for sure without additional testing and analysis of the precise substances on the plate.
Complete question:
The thin‑layer chromatography (TLC) plate shown was developed with 20% ethyl acetate in hexanes. (4) Suppose the plate had instead been developed with 5% ethyl acetate in hexanes. Determine whether each plate is a possible result of the adjusted development process and its conclusion.
To know more about Ethyl visit:
https://brainly.com/question/30313025
#SPJ4
Alguien que hable español?
jsjsjs
:)
Answers
Answer:
yo we xddd
Step-by-step explanation:
What is the sum of \(4 radical 3 +11 radical 12\)
Answers
The sum of 4√3 + 11√12 is 26√3.
What is Expression?An expression is combination of variables, numbers and operators.
We need to find the sum of 4radical3+11radical12
4√3 + 11√12
To find the solution we have to simplify the terms in the square root first.
4√3 + 11√4×3
4√3 + 11.2√3
4√3 + 22√3
26√3
So, the sum of 4√3 + 11√12 is 26√3.
To learn more on Expressions click:
https://brainly.com/question/14083225
#SPJ9
f(x)=3x+10
g(x)=x-2
find f(g(5)
Answers
Answer:
Step-by-step explanation:
g(5) = 5 - 2 = 3
f(3) = 3(3) + 10 = 9 + 10 = 19
please answer this, i'm not sure abt it nor have i seen the answer on here.

Answers
Answer:
t should be multipled by s
Step-by-step explanation:
r/s = t
r = t × s
Runners who achieved a time between 37 and 48 minutes to complete the race were each awarded a silver medal. (c) Calculate an estimate of the number or runners awarded silver medals
Answers
Answer:
The data is missing, However the answer is given below
Step-by-step explanation:
The data is missing about the runners and the duration minutes taken to complete the race, However the answer is given below
(3 * 4) + (8 * 3)
12 + 24
36 silver medals would have been awarded to runners.
The data is missing for the runners of the race and the time they took to complete the race, silver medal is awarded for runners who completed race in 37 to 38 minutes.
PLZZZ HELPPP I WILL AWARD BRAINLEIST!!!!!!
Factor -4 + 8a - 4a 2.
Answers
Given the system of linear equations ... \[ \left\{\begin{array}{c} x+2 y+3 z=9 \\ 2 x-y+z=8 \\ 3 x-z=3 \end{array}\right. \] 1) Write the system in the matrix form \( A . X=B \) (2 points) 2) Solve t
Answers
The solution of the system of equations is \(\[x=3,\text{ }y=0,\text{ and }z=2\]\).
As per data the system of linear equations,
\(\[ \left\{\begin{array}{c} x+2 y+3 z=9 \\ 2 x-y+z=8 \\ 3 x-z=3 \end{array}\right. \] 1)\)
Write the system in the matrix form \(\( A . X=B \)\)
We know that the matrix form of the system of linear equations is as follows.
\(\[A. X = B\]\)
Where
\(\[A=\begin{pmatrix} 1 & 2 & 3 \\ 2 & -1 & 1 \\ 3 & 0 & -1 \end{pmatrix}\[X=\begin{pmatrix} x \\ y \\ z \end{pmatrix}\]\)
and
\(\[B=\begin{pmatrix} 9 \\ 8 \\ 3 \end{pmatrix}\]2)\)
To solve the system, we can use row reduction method.
\(\[\begin{pmatrix} 1 & 2 & 3 & 9 \\ 2 & -1 & 1 & 8 \\ 3 & 0 & -1 & 3 \end{pmatrix}\]\)
Applying the elementary row operations
\(\[R_{2}\to R_{2}-2R_{1}\]\)
and
\(\[R_{3}\to R_{3}-3R_{1}\]\)
we get,
\(\[\begin{pmatrix} 1 & 2 & 3 & 9 \\ 0 & -5 & -5 & -10 \\ 0 & -6 & -10 & -24 \end{pmatrix}\]\)
Now applying the elementary row operations
\(\[R_{3}\to R_{3}-(6/5)R_{2}\]\)
we get,
\(\[\begin{pmatrix} 1 & 2 & 3 & 9 \\ 0 & -5 & -5 & -10 \\ 0 & 0 & -1 & -2 \end{pmatrix}\]\)
Now, we need to apply back substitution method. Using the third row, we can get the value of z as z = 2.
Now, using the second row,
\(\[-5y - 5z = -10\]\\\-5y - 5(2) = -10\]\)
Solving this equation, we get y = 0.
Finally, using the first row, we can get the value of x as
\(\[x + 2y + 3z = 9\]\\x = 3\]\)
Hence, the solution of the system of equations is \(\[x=3,\text{ }y=0,\text{ and }z=2\]\).
To learn more about linear equations from the given link.
https://brainly.com/question/2030026
#SPJ11
What are three consecutive odd integers of 57?
Answers
The required three consecutive odd numbers that sum up 57 are 17, 19 and 21.
What are consecutive numbers ?
Numbers that follow each other continuously in the order from smallest to largest are called consecutive numbers. For example: 1, 2, 3, 4, 5, 6, and so on are consecutive numbers.
Since, we know that any odd number is always of the form (2k +1). We express an odd number in this form because we know that an odd number is not divisible by 2.
Now, the next odd number after (2k+1) will be (2k+3) because if we take (2k+2) then we can see that it is clearly divisible by 2.
So, we can say that the difference between any two consecutive odd numbers is:
= 2k+3 – (2k+1)
=2k+3-2k-1
=2
So, for every two consecutive odd numbers there is a difference of 2.
Now, let us take ‘n’ to be an odd number.
So, an odd number just before n will be (n-2).
And also an odd number just after n will be (n+2).
Since, it is given that the sum of these three consecutive odd numbers is 57. So, we can write the following equation:
n-2+n+n+2=57
3n=57
So, n = 19
The odd number before n will be = n -2 = 19-2 = 17
And the odd number after n will be = n+2 = 19 + 2 = 21
Therefore, The required three consecutive odd numbers that sum up 57 are 17, 19 and 21.
Learn more about consecutive numbers at:
https://brainly.com/question/17296996
#SPJ4
1. A sample of 100 service times at a call center has a sample mean of 8 minutes and a sample standard deviation of 7 minutes. Assume that the service times are independent and have a normal distribution (a) Give a 95% confidence interval for the mean service time. (b) Approximately how many service times we would have to collect to return a 95% confidence interval whose width is at most 20 seconds (1/3 minute)?
Answers
We would need to collect at least 268 service times to return a 95% confidence interval whose width is at most 20 seconds.
(a) We can use the formula for a confidence interval for the mean of a normal distribution with known standard deviation:
CI = X ± z*(σ/√n)
where X is the sample mean, σ is the population standard deviation (in this case, the sample standard deviation is used as an estimate of the population standard deviation since it is known), n is the sample size, and z is the critical value from the standard normal distribution for the desired level of confidence.
For a 95% confidence interval, the critical value is z = 1.96. Plugging in the values, we get:
CI = 8 ± 1.96*(7/√100) = 8 ± 1.372
Therefore, a 95% confidence interval for the mean service time is (6.63, 9.37) minutes.
(b) To find the sample size required to return a 95% confidence interval whose width is at most 20 seconds, we can use the formula for the margin of error:
ME = z*(σ/√n)
where ME is the maximum allowed margin of error (which is 1/3 minute or 0.33 minutes in this case).
Solving for n, we get:
n = (z*σ/ME)^2
For a 95% confidence interval, the critical value is z = 1.96. Plugging in the values, we get:
n = (1.96*7/0.33)^2 ≈ 267.17
Therefore, we would need to collect at least 268 service times to return a 95% confidence interval whose width is at most 20 seconds.
To learn more about confidence interval visit: https://brainly.com/question/24131141
#SPJ11
10 = 10 2п 4nt 10 10 37 6nt 10 10 10 2.30 The Fourier series for the function y(t) = t for -5
Answers
This series converges to y(t) = t for -5 < t < 5.
To find the Fourier series of the function y(t) = t for -5 < t < 5, we can use the following formula:
c_n = (1/T) ∫(T/2)_(−T/2) y(t) e^(-jnω_0 t) dt
where T is the period of the function, ω_0 = 2π/T is the fundamental frequency, and n is an integer.
In this case, T = 10 and ω_0 = π. Thus, we have:
c_n = (1/10) ∫(-5)^(5) t e^(-jπnt/5) dt
Evaluating this integral using integration by parts, we get:
c_n = (1/π^2n^2)(-1)^n [2e^(jπn) - 2]
Therefore, the Fourier series of y(t) = t is:
y(t) = a_0 + ∑_(n=1)^∞ (c_n e^(jnω_0 t) + c_{-n} e^(-jnω_0 t))
where a_0 = c_0 = 0, and
c_n = (1/π^2n^2)(-1)^n [2e^(jπn) - 2], c_{-n} = (1/π^2n^2)(-1)^n [2e^(-jπn) - 2]
Therefore, the Fourier series of y(t) = t is:
y(t) = ∑_(n=1)^∞ [(1/π^2n^2)(-1)^n [2e^(jπn) - 2] e^(jnπt/5) + (1/π^2n^2)(-1)^n [2e^(-jπn) - 2] e^(-jnπt/5)].
This series converges to y(t) = t for -5 < t < 5.
Learn more about series here:
https://brainly.com/question/15415793
#SPJ11
solve pls brainliest

Answers
Answer:
\(18 {m}^{2} \)
Step-by-step explanation:
\(area \: = 6m \times 4m \\ = 24 {m}^{2} \\ \\ grass \: area = 3m \times 2m \\ = 6 {m}^{2} \\ \\ cement \: area \: = 24 {m}^{2} - 6 {m}^{2} \\ = 18 {m}^{2} \)
Answer:
18 m^2
Step by step explanation:
In these types of math problems, we have two ways to solve.
1) Directly find the area of the shaded area.
2)Find the unshaded area and then minus that from the total area.
In this case, I will use the second way.
The grass area (unshaded) is 3 x 2 = 6 m^2 ( 6 square meters )
The total area (grass + cement) is 4 x 6 = 24 m^2 ( 24 square meters )
Now, we want the area of the cement part but the grass's area is also in the total.
So, we minus 6m^2 from 24m^2.
Then we get 18m^2.
And that is the answer.
I hope it helps.
(Note : because this problem is easy, you can use both ways but most use the second way. There may also be problems where we can use only the first or second way.)
I can type 600 words in 12 minutes. How many words can I type in 1 minute.
Answers
In order to calculate how many words can you type in 1 minute we you use the rule of 3 to calculate the amount of words as follows:
you can type 600 words in 12 minutes therefore;
if 600 words____________________12 minutes
x_____________________1 minute
Therefore, the calculation would be:
x=words you can type in 1 minute
x=(600 words*1 minute)/12 minutes
x=50
Therefore, you can type a number of 50 words in 1 minute
Answer: 50 words
Step-by-step explanation: 600 divided by 12=50. 50x12=600
Find an equation for the plane containing the two (parallel) lines
v1 = (0, 1, −8) + t(6, 7, −5) and v2 = (8, −1, 0) + t(6, 7, −5).
Answers
The equation of the plane containing the two parallel lines v₁ = (0, 1, −8) t(6, 7, −5) and v₂ = (8, −1, 0) t(6, 7, −5) is 6x + 6y + 3z = 0.
What are parallel lines?
Parallel lines are coplanar infinite straight lines that do not intersect at any point in geometry. Parallel planes are planes that never meet in the same three-dimensional space. Parallel curves are those that do not touch or intersect and maintain a constant minimum distance.
To find an equation for the plane containing the two parallel lines v₁ = (0, 1, −8) t(6, 7, −5) and v₂ = (8, −1, 0) t(6, 7, −5),
We use the equation of a line: v = v₀ + tv₁
where v₀ and v₁ are points on the line and t is a real number.
Substitute the given points in for v₀ and v₁: v = (0, 1, −8) + t(6, 7, −5)
This equation of the plane is Ax + By + Cz = D, where A, B, C, and D are constants to be determined.
Equate the components:
0x + 1y - 8z = D....(1)
6x + 7y - 5z = D...(2)
Now, we subtract equation (1) from (2) and we get
6x - 0x + 7y - 1y - 5z + 8z = 0
6x + 6y + 3z = 0
Hence, the equation of the plane containing the two parallel lines v₁ = (0, 1, −8) t(6, 7, −5) and v₂ = (8, −1, 0) t(6, 7, −5) is 6x + 6y + 3z = 0.
To learn more about the parallel line from the given link
https://brainly.com/question/24607467
#SPJ4
The wheels on a bike have a diameter of 26 inches. How many full revolutions will the wheels need to make to travel 100 feet? A. 4 revolutions B. 8 revolutions C. 15 revolutions D. 82 revolutions
Answers
Answer:
C) 15 revolutions
Step-by-step explanation:
one revolution is the measure of the wheel's circumference, which is 26π inches
26π is about 81.7 inches or 6.8 feet
100 ÷ 6.8 is 14.7
therefore, you would need to round up to 15 revolutions
What is the solution to this equation?
−15(x+134)=−212
Responses
x=2114
x equals 21 and 1 over 4
x=1414
x equals 14 and 1 over 4
x=1034
x equals 10 and 3 over 4
x=334
Answers
Answer: 10 3\4
Step-by-step explanation:
I did the quiz
The product of the ages of three children is 1872. The age of the middle child is the average of the ages of the other two children. What is the sum of their ages
Answers
When the product of the ages of three children is 1872, the age of the middle child is the average of the ages of the other two children, then the sum of their ages is 57.
Let, the ages of the three children as A, B, and C.
Given that the product of their ages is 1872, we have:
A * B * C = 1872
Given that the age of the middle child is the average of the ages of the other two children, we can write:
B = (A + C) / 2
Now we have a system of two equations:
A * B * C = 1872
B = (A + C) / 2
We can substitute the value of B from the second equation into the first equation:
A * ((A + C) / 2) * C = 1872
Simplify the equation:
A * (A + C) * C = 3744
Now, we have a quadratic equation in terms of A and C.
\(A^2 * C + AC^2 = 3744\\AC(A + C) = 3744\\AC^2 + AC^2 = 3744\\2AC^2 = 3744\\AC^2 = 1872\\C^2 = 1872 / A\)
Since the ages are positive integers, we need to find a pair of positive integers A and C such that \(A * C^2 = 1872\).
Let's look for factors of 1872 that can work for \(C^2\):
\(1872 = 2^4 * 3^2 * 13\)
The possible pairs of A and C are:
A = 1, C = 1872
A = 2, C = 936
A = 3, C = 416
A = 4, C = 234
A = 6, C = 104
A = 8, C = 58
A = 12, C = 26
Since A and C are ages, we'll choose A = 12 and C = 26.
Now we can find B using the equation B = (A + C) / 2:
B = (12 + 26) / 2 = 38 / 2 = 19
The sum of their ages is:
A + B + C = 12 + 19 + 26 = 57
Therefore, the sum of their ages is 57.
To learn more on equation click:
https://brainly.com/question/14468218
#SPJ12
The dimensions, in centimetres, of this rectangle are shown as algebraic expressions.
Not to scale
5x-y-8
3x + y-4
2x-6-3
3x + 5y +4
Work out the length and width of the rectangle.

Answers
Answer:
length = 15
Width = 9
Step-by-step explanation:
In a rectangle opposite sides are equal.
5x - y- 8 =3x +5y + 4
5x - 3x -y - 5y = 4 + 8
2x - 6y = 12
Divide the entire equation by 2
x - 3y = 6 --------------(I)
3x + y - 4 = 2x - 6y - 3
3x - 2x + y + 6y = -3 + 4
x + 7y = 1 -------------(II)
Multiply equation (II) by (-1)
(I) x - 3y = 6
(II)*(-1) -x - 7y = -1 {Now add. 'x' will be eliminated}
-10y= 5
y = 5/(-10)
y = -0.5
Plugin y = -0.5 in equation (I)
x - 3*(-0.5) = 6
x + 1.5 = 6
x = 6 - 1.5
x = 4.5
Length = 5x - y - 8
= 5*4.5 - (-0.5) - 8
= 22.5 + 0.5 - 8
= 23 - 8
Length = 15
Width = 2x - 6y - 3
= 2*4.5 - 6*(-0.5) - 3
= 9 + 3 - 3
Width = 9
A scale drawing of a room is shown below. In the drawing, the room is 7 inches long and 5 inches wide. What is the actual area of the room?
75ft^2
37 1/2 ft^2
150 ft^2
50 ft^2
please help TvT
Answers
Answer:
the actual area of the room is 35 inches
Step-by-step explanation:
you have to multiply 7 by 5.
Multiply 7 by 5 which is 35
two marbles are randomly selected without replacement from a bag containing blue and green marbles. the probability they are both blue is . if three marbles are randomly selected without replacement, the probability that all three are blue is . what is the fewest number of marbles that must have been in the bag before any were drawn? (2000 mathcounts national target)
Answers
The probability of selecting two blue marbles without replacement is 1/6, and the probability of selecting three blue marbles without replacement is 1/35. The fewest number of marbles that must have been in the bag before any were drawn is 36.
Let's assume there are x marbles in the bag. The probability of selecting two blue marbles without replacement can be calculated using the following equation: (x - 1)/(x) * (x - 2)/(x - 1) = 1/6. Simplifying this equation gives (x - 2)/(x) = 1/6. Solving for x, we find x = 12.
Similarly, the probability of selecting three blue marbles without replacement can be calculated using the equation: (x - 1)/(x) * (x - 2)/(x - 1) * (x - 3)/(x - 2) = 1/35. Simplifying this equation gives (x - 3)/(x) = 1/35. Solving for x, we find x = 36.
Therefore, the fewest number of marbles that must have been in the bag before any were drawn is 36.
Learn more about probability here: https://brainly.com/question/31828911
#SPJ11
What is the measure of
Answers
Answer: measure of what ?
Step-by-step explanation:
Copy the axes below.
a) By completing the tables of values to help you, plot the lines
y=x+6 and y=-2x + on your axes.
b) Use your diagram to find the solution to the simultaneous equations
y = x + 6 and y = -2x +
3
y=x+6
-40 4
Y
y = -2x + ²
x-1 0 1
Y
6
5
4
3
2
14
-3 -2 51 10
2

Answers
Using graph to solve the system of linear equations, the value of x is -2 and y is 5.5
What is the solution to the linear equationsIn the given problem, we are asked to find the solution to the simultaneous linear equations;
y = 1/4x + 6
y = -2x + 3/2
In the problem, we are asked to plot this and use the solution from the graph to determine the value of x and y.
The solution of system of linear equation is determine from the point of intersection of the the two linear lines.
Plotting the linear equations on a graphing calculator;
From the graph attached below, the point of intersection is at (-2, 5.5) and this shows the value of x is -2 and y is 5.5
Learn more on system of linear equations here;
https://brainly.com/question/13729904
#SPJ1

i need help with these two pls answer if u know how to do dis

Answers
a) The Total area of figure is 128.5 in²
b) Total area of the figure is 36.54 m
Define the term rectangle and triangle?A triangle is a three-sided, triangular geometric shape. The sum of the angles in a triangle is always 180 degrees.
a). Two rectangles are present,
Area of Rectangle 1 = 12 in × 8 in = 96 in²
Area of Rectangle 2 = 6.5 in × 5 in = 32.5 in²
Total area of figure = 96 + 32.5 = 128.5 in²
b). One triangle and one rectangle are present.
Area of Rectangle = 7.8 m × 4.2 m = 32.76 m²
Area of triangle = 1/2 × base × height
Area of triangle = 1/2 × 4.2m × 1.8 m = 3.78 m²
Total area of the (figure (b) = Area of Rectangle + Area of triangle
Total area of the figure = 32.76 m² + 3.78 m²
To know more about rectangle, visit:
brainly.com/question/2607596
#SPJ1

From the 4380 Science students on campus, a random sample of 219 students are selected. Out of this sample, 177 was found to have a height over 1.80 m. Use a 95% left-sided confidence interval to estimate the true proportion of tall students. Are any of the conditions required for a valid interval violated? How many conditions are violated? (Only type the number) If it is possible to calculate a confidence interval, enter the confidence limits in the provided spaces (rounded to at least 3 decimal places). If it is not possible to calculate a confidence interval, then enter 0 for both limits. [ ] Is 63% a possible true percentage of tall Science students? Yes Or NO
Answers
The 95% left-sided confidence interval for the true proportion of tall students is approximately 0.825.If 63% is a possible true percentage of tall Science students. Since 63% is outside the interval is NO.
To determine if any conditions are violated and calculate a confidence interval for the true proportion of tall students, the formula for a confidence interval for a proportion:
p ± Z × √((p× q ) / n)
Where:
P is the sample proportion (177/219)
q is the complement of the sample proportion (1 - p)
n is the sample size (219)
Z is the Z-score corresponding to the desired confidence level (95% left-sided corresponds to a Z-score of -1.645)
calculate the confidence interval:
p = 177/219 =0.807
q = 1 - p = 1 - 0.807 =0.193
n = 219
Z = -1.645
Confidence interval formula:
0.807 ± -1.645 ×√((0.807 × 0.193) / 219)
Calculating the confidence interval:
0.807 ± -1.645 × √(0.156051 / 219)
0.807 ± -1.645 × 0.010941
0.807 ± -0.017989
0.789 to 0.825 (rounded to three decimal places)
To know more about percentage here
https://brainly.com/question/28998211
#SPJ4
What is the simplest form of 3/3/8 + 5/12 help pleaseeee
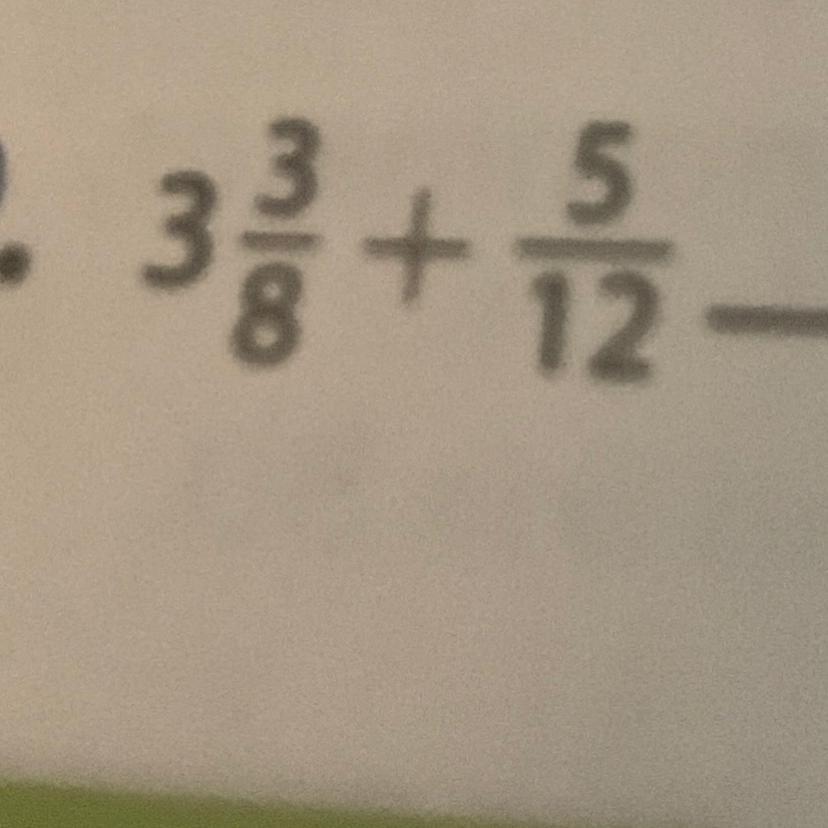
Answers
Answer:
it is 27/50 is already in simplist form
Step-by-step explanation:
brainliest plzzzz
Answer:
3.791666 in decimals.
91/24 in fraction form.
Step-by-step explanation:
Hope it helps.
