use the confidence level and sample data to find a confidence interval for estimating the population μ. round your answer to one decimal place.
a group of 64 randomly selected students have a mean score of 38.6 with a standard deviation of 4.9 on a placement test. what is the 90% confidence interval for the mean score, μ, of all students taking the test?
Answers
The 90% confidence interval for the mean score, μ, of all students taking the test is (37.6, 39.6).
To find the confidence interval for estimating the population mean score, we can use the following formula:
CI = x ± z*(σ/√n)
Where:
x = sample mean score = 38.6
σ = population standard deviation (unknown)
n = sample size = 64
z = z-score for the desired confidence level, which is 1.645 for 90% confidence interval
First, we need to estimate the population standard deviation using the sample standard deviation:
s = 4.9
Next, we can plug in the values into the formula:
CI = 38.6 ± 1.645*(4.9/√64)
= 38.6 ± 1.645*(0.6125)
= 38.6 ± 1.008
= (37.6, 39.6)
Therefore, the 90% confidence interval for the mean score, μ, of all students taking the test is (37.6, 39.6).
Read more about Confidence Interval at; brainly.com/question/17097944
#SPJ11
Related Questions
For every $1 increase in the price per scarf, Sofie's profit changes by an average of $
Answers
Answer:
True, because if price changes, dod oes average of money. So if you get 5 bucks per 10 scarfs, you'll get 5.50$ for 11 scarfs
Step-by-step explanation:
Lets just say she gets half of what the actual cost is. In total.
Answer:
This is true
Step-by-step explanation:
2. is 5/8 greater than, less than or equal to 11/16
Answers
Answer:
less than
Step-by-step explanation:
Convert –18° to radians.
Answer: D on edg (- pie/10 radians)
Answers
Answer:
\(-\frac{\pi }{10}\) radians
Step-by-step explanation:
Miguel and three of his friends went to the movies. They originally had a total of $40. Each boy had the same amount of money and spent $7.50 on a ticket. How much money did each boy have left after buying his ticket?
A. Draw a bar diagram that represents the situation.
B. Write and solve an equation that represents the situation.
C. Explain how you solved your equation.
D. Compare the arithmetic solution and the algebraic solution.
Answers
I might be wrong
91 is 70% of what number?91 is 70% of what number?
Answers
Answer: 91 is 70% of 130
Step-by-step explanation:
:)
Answer:
130
Step-by-step explanation:
70% of 130 = 91
Simplify the expression

Answers
Answer:
\(2\)
Step-by-step explanation:
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition SubtractionStep 1: Write expression
\(\frac{12/2(3)}{3(3)}\)
Step 2: Evaluate
Divide: \(\frac{6(3)}{3(3)}\)Multiply: \(\frac{18}{3(3)}\)Multiply: \(\frac{18}{9}\)Divide: \(2\)what is the equation for the line that is parallel to the y-axis and passes through the point (2, -5)?
Answers
Answer:
X = 2
Step-by-step explanation:
Which of the following is a counterexample to the given statement?
The name of every month ends in the letter y.
a. January
b. July
C February
d. December
Answers
The name of every month ends in the letter y is the given statement. February is a counterexample to this statement. This is because February does not end with the letter 'y'. So the right option is (c) February.
What is a counterexample?
In mathematics, a counterexample is an example that opposes or disproves a statement, proposition, or theorem. It is a scenario, an instance, or an example that goes against the given statement.
Therefore, a counterexample demonstrates that the given statement is false or invalid.In this case, the statement is: "The name of every month ends in the letter y." We have to find which of the months listed does not end in "y."February is the only month in the options listed that does not end in the letter "y."
Thus, it is a counterexample to the given statement. Therefore, the correct option is C, February.
For more questions on: counterexample
https://brainly.com/question/29197877
#SPJ8
A scientist began a study with a sample of 1,500 bacteria. He noticed that the number of bacteria in the sample after t days can be modeled by the equation P=1,500 • 5t . In this equation, what does 5t represent? A. The number of bacteria increases by 5 bacteria each day. B. The number of bacteria increases by a factor of t each day for 5 days. C. The number of bacteria increases by a factor of 5 each day. D. The number of bacteria increases by t bacteria after 5 days.
Answers
The correct answer is the number of bacteria increases by a factor of 5 each day. I've tooken a quiz on it
The correct answer A that the number of bacteria increases by a factor of 5 each day.
What is a linear equation?A linear equation is an equation that has the variable of the highest power of 1. The standard form of a linear equation is of the form Ax + B = 0.
It is said that a scientist began a study with a sample of 1,500 bacteria.
He noticed that the number of bacteria in the sample after t days can be modeled by the equation P = 1,500 x 5t.
Here, the equation is given P = 1,500 x 5t.
So, 5t terms represent the number of bacteria increases by 5 bacteria each day.
The correct answer is the number of bacteria increases by a factor of 5 each day.
Learn more about linear equations;
https://brainly.com/question/27056029
The temperature is 2 ∘F and drops to −15 ∘F overnight. Write and then evaluate a subtraction expression to determine the temperature change.
Enter the correct answers in the boxes.
Expression:
a
Temperature change:
∘F
Answers
I assume that F (is the variable) it’s what’s missing from the equation. The change i. temperature. To find F add 2 +(-15) which is -13 so the change in temperature is -13
please help i will mark brainlist

Answers
Answer:
In order to use the Pythogrean theorem you must first use the points to form a triangle then count the side length in order to get your numbers. It should be 7^2+2^2=c^2 and your answer should be 7.28. This person subtracted the x coordinates from the x coordinate and the y from the y to get their numbers.
Step-by-step explanation:
Express the area of the entire rectangle
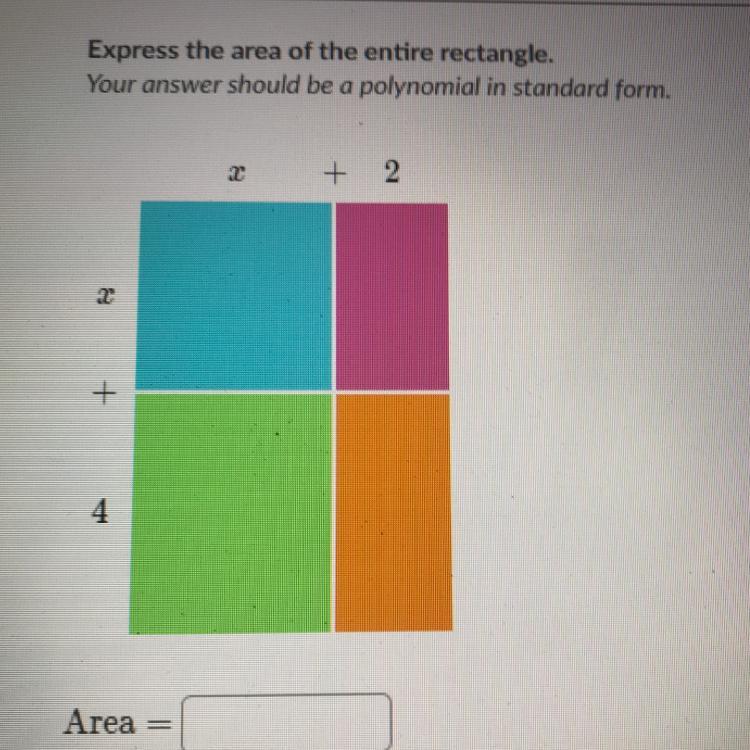
Answers
Answer:
x^2 + 6x + 8
Step-by-step explanation:
area of blue = x^2
area of pink= 2x
area of green=4x
area of brown=8
Adding all the area.
we get : x^2 + 6x +8
Pls halp due today >_<. Thank you

Answers
Whole, integer, rational, real
CAN SOMEONE PLS HELP ME WITH THIS MATH

Answers
Answer:
1. 3) measure of angle 3 and measure of angle 5 are supplementary
2. x=16
Factor the polynomial and use the factored form to find the real zeros. (Enter your answers as a comma-separated list. Enter all answers including repetitions.)
P(x) = x³ + x² − x − 1
Answers
The real zeros of P(x) are 1, −1, and −1.
We have,
To factor the given polynomial P(x) = x³ + x² − x − 1, we can use the Rational Root Theorem and synthetic division to find one of its roots, and then factor out the corresponding linear factor.
The constant term of P(x) is −1, and the leading coefficient is 1, so any rational root of P(x) must have a numerator that is a factor of −1 and a denominator that is a factor of 1.
Thus, the possible rational roots of P(x) are ±1 and ±1/1 = ±1.
To check which of these possible roots is actually a root of P(x), we can use synthetic division:
1 | 1 1 -1 -1
| 1 2 1
|-------------
| 1 2 1 0
Since the remainder is 0, we have found that 1 is a root of P(x), and we can write:
P(x) = (x − 1)(x² + 2x + 1)
The quadratic factor can be factored further as (x + 1)².
So,
P(x) = (x − 1)(x + 1)²
The real zeros of P(x) are the values of x that make P(x) equal to 0.
These occur when x = 1, and x = −1 (twice).
Therefore,
The real zeros of P(x) are 1, −1, and −1.
Learn more about polynomials here:
https://brainly.com/question/2284746
#SPJ1
Expand.Put this in polynomial standard form (Y2-9)(y2-4)=
Answers
Just multiply both, and simplify by collecting like terms
Solve the following Find allsolutions on the interval 0 <= x < 2π.
Give exact solutions when possible. Found to 4 decimal place.
a) cos(2x) = 0
b) cos2x - cosx + 1 = 0
Answers
a) To find the solutions to the equation cos(2x) = 0 on the interval 0 <= x < 2π, we can use the property double-angle identity of cosine that states when the cosine of an angle is zero, the angle must be an odd multiple of π/2.
Therefore, we have two cases to consider: 2x = (2n + 1)π/2, where n is an integer. For the first case, solving 2x = (2n + 1)π/2 for x, we have x = (2n + 1)π/4, where n is an integer. Since we want the solutions within the interval 0 <= x < 2π, we can substitute n = 0, 1, 2, and 3 to find the solutions in that range: x = π/4, 3π/4, 5π/4, and 7π/4. The solutions to cos(2x) = 0 on the interval 0 <= x < 2π are x = π/4, 3π/4, 5π/4, and 7π/4.
Learn more about double-angle identity here : brainly.com/question/30402758
#SPJ11
solve the equation simultaneously:
y = 2-2x
y = -16 + 2(x-3)^2
Answers
Answer:
y = -26
Step-by-step explanation:
[y = 2 - 2x] + [y = -16 + 2(x - 3)^2]
y = -16 + 2x - 6^2
y = -16 + 2x - 6^2 + 2 - 2x
y = (+2x - 2x) - 16 - 6^2 + 2
y = -16 - 6^2 + 2
y = -16 - 12 + 2
y = - 28 + 2
y = -26
For the standard normal probability distribution, the area under the probability density function to the left of the mean is.
Answers
For the standard normal probability distribution, the area under the probability density function to the left of the mean is 0.5.
This means that half of the distribution lies to the left of the mean, and the other half lies to the right. Since the distribution is symmetric, the area under the curve to the left of the mean is equal to the area under the curve to the right of the mean. Therefore, both areas are 0.5 or 50%.
In a standard normal distribution, the probability density function (PDF) is symmetric about the mean. This means that the area under the curve to the left of the mean is equal to the area under the curve to the right of the mean.
Since the total area under the curve represents the probability of the entire distribution, it sums up to 1. Therefore, when we divide the distribution into two equal parts, each part represents 0.5 or 50% of the total area.
To know more about standard normal probability distribution,
https://brainly.com/question/32577342
#SPJ11
10. A cone has a Volume of 94.25cm ^ 3 If the radius of the cone is 3 cm, what is the height of the cone?
Answers
Answer:
10 cm
Step-by-step explanation:
V =1/3 x π x r² x h
94.25 =1/3 x π x 3² x h
94.25 ÷ 3π =h
so, h= 10 cm
Find the x-intercept and y-intercept
from the following linear equation:
- 7x + 4y = 56
x-intercept ([?],[ ])
y-intercept ([?],[ ])
Answers
y= 7/4x + 14
Among 1,000 applicants for admission to MSC Statistics course in a University, 600 were statistics graduates and 400 were non-statistics graduates; 30% of statistics graduate applicants and 5% of non-statistics graduate applicants obtained admission. If an applicant selected at random is found to have been given admission, what is the probability that he or she is an statistics graduate?
Answers
the probability that an admitted applicant is a statistics graduate is approximately 0.818 (or 81.8%) when rounded to one decimal place.
We can use Bayes' theorem to calculate the probability that an admitted applicant is a statistics graduate. Let A represent the event that an applicant is a statistics graduate, and B represent the event that an applicant is admitted. Then, we want to find P(A|B), the probability that an admitted applicant is a statistics graduate.
Using the given information, we can determine the following probabilities:
P(A) = 600/1000 = 0.6
P(B|A) = 0.3
P(B|A') = 0.05
where P(A') represents the complement of event A (i.e., an applicant is not a statistics graduate).
We can now apply Bayes' theorem:
P(A|B) = P(B|A)P(A) / [P(B|A)P(A) + P(B|A')P(A')]
Substituting the given probabilities, we get:
P(A|B) = (0.3)(0.6) / [(0.3)(0.6) + (0.05)(0.4)]
P(A|B) = 0.818
Therefore, the probability that an admitted applicant is a statistics graduate is approximately 0.818 (or 81.8%) when rounded to one decimal place.
To know more about statistics related question visit:
https://brainly.com/question/31577270
#SPJ11
.
.
On Monday, she drove 4 to hours.
On Tuesday, she drove 5 to hours.
On Wednesday, she drove 3 hours.
.
How many hours altogether did Taniya drive on her trip?
A
1210
B
13
C
lo
13.10
14
D
Answers
Answer:
She drove 12 hours
5+4+3=12
Step-by-step explanation:
Find the derivative of the function at P in the direction of A f(x,y,z):xy + yz + zx, (1,-1,-2), A = 3i + 2j - 6k (DAf) | 1(1,-1,-2) =
Answers
Therefore, the directional derivative of f at P=(1,-1,-2) in the direction of A=3i+2j-6k is -2.
To find the directional derivative of f(x,y,z) at P=(1,-1,-2) in the direction of A=3i+2j-6k, we first need to find the gradient of f at P, which is given by:
grad(f) = ∇f = (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k
Here, f(x,y,z) = xy + yz + zx, so we have:
∂f/∂x = y + z
∂f/∂y = x + z
∂f/∂z = x + y
Thus, at P=(1,-1,-2), we have:
∇f(P) = (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k
= (y+z)i + (x+z)j + (x+y)k
= (0+(-2))i + (1+(-2))j + (1+0)k
= -2i - 1j + 1k
Next, we need to find the unit vector in the direction of A:
|A| = sqrt(3^2 + 2^2 + (-6)^2) = 7
u = A/|A| = (3/7)i + (2/7)j - (6/7)k
Finally, we can compute the directional derivative of f at P in the direction of A as:
(DAf) | 1(1,-1,-2) = ∇f(P) · u
= (-2i - 1j + 1k) · (3/7)i + (2/7)j - (6/7)k
= -6/7 - 2/7 - 6/7
= -2
To know more about derivative,
https://brainly.com/question/29752525
#SPJ11
draw the image of △ △abctriangle, a, b, c under a dilation whose center is pp and scale factor is 1 2 2 1 start fraction, 1, divided by, 2, end fraction.
Answers
The resultant triangle is shown below. The resulting triangle PQR is the image of the original triangle ABC under the given dilation with center P and scale factor 1/2.
To draw the image of △ ABC triangle under a dilation with center P and scale factor 1/2, follow these steps:
Locate point P: Identify point P, the center of dilation, on the coordinate plane.
Plot the original triangle ABC: Plot the three given points A(0,6), B(-6,0), and C(6,0) to form the original triangle ABC.
Calculate the new coordinates: To find the new coordinates A', B', and C', multiply the x and y coordinates of each point by the scale factor 1/2. For instance, the new coordinates of point A' would be
\((0 \times 1/2, 6 \times 1/2) = (0, 3).\)
Draw the new triangle PQR: Connect the new points A', B', and C' to form the image triangle PQR.
Therefore the resulting triangle PQR is the image of the original triangle ABC under the given dilation with center P and scale factor 1/2. The new triangle will be smaller than the original, with sides reduced by a factor of 1/2.
Learn more about geometric transformations here:
https://brainly.com/question/29987040
#SPJ12

You start a savings account and on the first week you deposit $2. Every
week you add $1 more to the account then the week before. So on the
second week you add $3, on the third week $4. On which week would the
account be worth $560?
Answers
Answer:
558 weeks
Step-by-step explanation:
let x = number of weeks
this equation can be derived from the question
2 + 1x = 560
collect like terms
x = 560 - 2
x = 558
Given the coordinates below, determine if ΔFGH and ΔJKL are congruent. If they are, give the reason, if they aren't choose "not congruent".
F(-5, 10), G(-2, 2), H(-9, -7), J(0, -5), K(9, 2), L(-8, -2)
*enter your lengths to the NEAREST TENTH
FG =
GH =
FH =
JK =
KL =
JL =
Answers
Answer:
FG≅LJ
GH≅JK
HF≅KL
Step-by-step explanation:
Suppose a spring with spring constant 3 N/m 3 N m is horizontal and has one end attached to a wall and the other end attached to a 4 kg 4 k g mass. Suppose that the friction of the mass with the floor (i.e., the damping constant) is 3 N⋅s/m 3 N s m .
Set up a differential equation that describes this system. Let x x to denote the displacement, in meters, of the mass from its equilibrium position, and give your answer in terms of x,x′,x′′ x x ′ x ′ ′ . Assume that positive displacement means the mass is farther from the wall than when the system is at equilibrium.
Find the general solution to your differential equation from the previous part. Use c1c1 and c2c2 to denote arbitrary constants. Use tt for independent variable to represent the time elapsed in seconds. Enter c1c1 as c1 and c2c2 as c2. Your answer should be an equation of the form x=…x.
Enter a value for the damping constant that would make the system critically damped.
Answers
The required differential equation is x'' + 0.67x' + 2.33x = 0.
The standard differential equation, which we use to represent a damped spring-mass system is written as:
m(d²x/dt²) + c(dx/dt) + kx = 0,
where m is the mass, c is the damping coefficient, k is the spring constant, x is the d²splacement, and the equation has been derived with respect to time t.
In the question, the
mass m = 3 kg,
spring constant k = 7 N/m,
damping constant c = 2N-s/m.
Differentiating x with time t, we take (d²x/dt²) = x'', and (dx/dt) = x'.
Substituting all the values in the standard differential equation, we get:
3x'' + 2x' + 7x = 0,
or, x'' + (2/3)x' + (7/3)x = 0 {Dividing by 3},
or, x'' + 0.67x' + 2.33x = 0, which is the required differential equation.
Learn more about differential equations at
https://brainly.com/question/13557017
#SPJ4
The provided question is incorrect. The correct question is:
"Suppose a spring with a spring constant of 7 N/m is horizontal and has one end attached to a wall and the other end attached to a 3 kg mass. Suppose that the friction of the mass with the floor (i.e., the damping constant) is 2 N⋅s/m. Set up a differential equation that describes this system. Let x denote the displacement, in meters, of the mass from its equilibrium position, and give your answer in terms of x, x′, x′′. Assume that positive displacement means the mass is farther from the wall than when the system is at equilibrium."
(1+2.46^2) ÷ 2+3.5^2
Answers
Answer:0.4948
Step-by-step explanation:
(1+2.46^2) ÷ 2+3.5^2
(1+6.052) ÷ (2+12.25)
7.052/14.25
0.4948
Answer: 15.77
Step-by-step explanation:
How do you solve for x in an angle?
Answers
To solve for x at an angle, you must first understand what type of angle you are working with. If the angle is a right angle, you can use the Pythagorean theorem to solve for x. If the angle is an obtuse angle, you can use the law of cosines to solve for x. If the angle is an acute angle, you can use the law of sines to solve for x.
How to solve for x at a right angle?To solve for x at a right angle using the Pythagorean theorem, you must have the lengths of the two neighboring sides of the triangle. The sum of the squares of the two sides is equal to the square of the hypotenuse, according to the Pythagorean theorem. By rearranging the components and solving for x, this equation may be used to find x.
How to solve for x at an obtuse angle?To use the law of cosines to solve for x at an obtuse angle, you must know the lengths of all three sides of the triangle. According to the law of cosines, the square of one side's length equals the sum of the squares of the other 2 sides minus twice the product of the other 2 sides multiplied by the cosine of the obtuse angle. You can use this equation to solve for x by rearranging the terms and solving for x.
How to solve for x in an acute angle?To apply the law of sines to solve for x in an acute angle, you should first know the lengths of the triangle's two sides as well as the acute angle's measurement. According to the law of sines, the ratio of one side's length to the sine of the opposite angle equals the ratio of the other side's length to the sine of the acute angle. By rearranging the terms and solving for x, you may use this equation to solve for x.
Learn more about acute angle here: brainly.com/question/6979153
#SPJ4