What integer is closest to the radius of a circle with a circumference of 50.27?

Answers
The integer which is closest to the radius of a circle with a circumference of 50.27 as required is; Choice A; 8.
Which answer choice is closest to the radius of the circle?It follows from the task content that the integer which is closest to the radius of the circle whose circumference is; 50.27 is to be determined.
Recall; Circumference, C = 2πr
r = C / 2π
r = 50.27 / 2π
r = 8.000718989
Ultimately, the integer which is closest to the radius is; Choice A; 8.
Read more on circumference of a circle;
https://brainly.com/question/18571680
#SPJ1
Related Questions
Elizabeth has $26 left after shopping at the mall. She bought 2 shirts for $22.99 each, a drink for $2.02, and 2 books for $16 each. How much money did she start with?
Answers
Step-by-step explanation:
22.99 × 2 + 2.02 + 16 × 2 + 26= $106
Situe no mesmo sistema de eixos cartesianos os pontos A(1, 3), B(-2, 1), C(0, -4), D(-3, 0), E(-2, -3), F(2, -1), G(3, -4) e H(5/2, ½).
Answers
Answer:
A,D,F,E
Step-by-step explanation:
• Los médicos pueden recetar los mismos medicamentos a los niños y a los adultos.
La fórmula utilizada, conocida como regla de Fried, es la siguiente: d= 0.08 AD,
donde des la dosis del niño, a es la edad del niño y D es la dosis del adulto. Si el
médico le receta 1,000 mg de acetaminofén a un adulto, ¿cuántos mg le debe de
recetar a un niño de 8 años?
Answers
Evaluando la función dada, veremos que la dosis para el niño debe ser 640 mg.
¿Cual será la dosis que se debe recetar al niño?
La funcion que debemos utilizar es:
d = 0.08*A*D
Donde, A es la edad del niño, en este caso: A = 8
D es la dosis correspondiente para un adulto, D = 1,000 mg
Reemplazando eso obtenemos:
d = 0.08*8*1,000mg = 640mg
Así, podemos concluir que al niño se le debe recetar una dosis de 640 mg.
Sí quieres aprender más sobre evaluaciones, puedes leer:
https://brainly.com/question/4344214
What the answer plsssssssss

Answers
Pamela prepared 16 kilograms of dough after working 2 hours. How many hours did Pamela
work if she prepared 72 kilograms of dough? Solve using unit rates.
hours
Answers
Answer:
Pamela worked 9 hours if she prepared 72 kilograms of dough.
Step-by-step explanation:
First we divide 72 by 16.
72 ÷ 16 = 4.5
Next we multiply 4.5 by 2.
4.5 * 2 = 9
So, the answer is 9 hours.
Hope this helps! :)
what is 999.09344471 rounded to the nearest square kilometer?
Answers
The nearest kilometers to 999.09344471 km is 1000 km.
Given value is 999.09344471 Km.
We have to calculate the round off value to the nearest kilometers. we know that after the decimal if the value of tenth place is 5 or bigger than 5 then we add 1 to the tens place digit, this is the fundamental rule of rounding off.
Now on following this rule from the very right hand side up to the tenth place digit we come to the conclusion that only the value after the decimal (934) is to be rounded off which is (900).
So 999.09344471 km is finally becomes 999.900 km after rounding of to nearest hundredth value.
Again rounding off 999.900 km to nearest km so it becomes 1000 km.
The nearest kilometers to 999.09344471 km is 1000 km.
For more details on round off follow the link:
brainly.com/question/1093198
Find the coordinates of the point of intersection of the diagonals of parallelogram ABCD with the vertices:A(-1,3), B (3,3), C (5, -1), and D (1, -1)
Answers
Solution
Part 1
We have the following points given:
A (-1,3) B(3,3) C(5, -1) and D(1, -1)
The diagonals for this case are:
AC and BD
Then we can find the midpoint with the following points:
A (-1,3) C(5,-1)
\(x=\frac{x_1+x_2}{2}=\frac{-1+5}{2}=2\)\(y=\frac{y_1+y_2}{2}=\frac{3-1}{2}=1\)Then the midpoint would be:
(2,1)
Part 2
For this case we have the following points:
P(-3,2) Q(2,6) R(3,3) S(x,y)
We need to satisfy the following:
slope PS= slope QR
And replacing we got:
\(\frac{y-2}{x+3}=\frac{3-6}{3-2}\)Solving we have the following equation:
(y-2) = (x+3)*-3
y -2= -3x-9
y= -3x -7
Then we can create this other equation:
slope PQ = slope RS
replacing we got:
\(\frac{y-3}{x-3}=\frac{6-2}{2+3}\)Solving we got:
5(y-3) = 4(x-3)
5y-15 =4x-12
5y -4x = 3
Replacing the first equation we got:
5(-3x-7) -4x= 3
-15x -35 -4x = 3
-19 x= 38
x= -2
y= -3*(-2)-7= 6-7 =-1
Then the answer is:
S= (-2,-1)
Part 3
We have the following points:
A= (-3,4)
B= (3,2)
C=(2,-1)
D=(-4,1)
We can find the distance between points like this:
\(d_{AB}=\sqrt[]{(3+3)^2+(2-4)^2}=\sqrt[]{40}\)\(d_{BC}=\sqrt[]{(2-3)^2+(-1-2)^2}=\sqrt[]{10}\)\(d_{CD}=\sqrt[]{(-4-2)^2+(1+1)^2}=\sqrt[]{40}\)\(d_{DA}=\sqrt[]{(-4+3)^2+(1-4)^2}=\sqrt[]{10}\)Then AB= DA and BC= CD
Then the answer is:
Parallelogram
Rectangle
Would you mind the window ?
Answers
Kira and Jake are building towers. Each one of Kira's blocks is 9 cm tall. Each one of Jake's blocks is 12 cm tall. They both build towers that are exactly the same height. What is the smallest height that their towers could be? Give your answer in centimetres (cm).
Answers
The smallest height of the towers is 3 cm.
We have,
Grace:
Kira's = 9 cm
Jake:
Blocks = 12 cm
Now, Kira and Jake build towers that are exactly the same height.
To find the smallest height we have to find the Least Common Multiple.
9 = 3 x 3
12= 2 x 2 x 3
So, LCM(9, 12) = 3
Thus, the smallest height of tower is 3.
Learn more about Least Common Multiple here:
https://brainly.com/question/28882807
#SPJ1
If there are penguins in the aquarium is full of fish, then this is an octopus write
this in Symbolic form

Answers
The compound statement "If there are penguins and the aquarium is full of fish, then this is an octopus" can be written in symbolic form as: r ∧ q → o
How to explain the informationLet's assign variables to represent the statements:
q: The aquarium is full of fish.
r: There are penguins.
The compound statement "If there are penguins and the aquarium is full of fish, then this is an octopus" can be written in symbolic form as: r ∧ q → o
∧ represents the logical operator "and" which connects the statements r and q.
→ represents the logical operator "implies" or "if...then".
o represents the statement "this is an octopus".
Learn more about compound statement on
https://brainly.com/question/28794655
#SPJ1
Sasha's retirement party will cost $15 if she invites 3 guests. What is the maximum number of guests there can be if Sasha can afford to spend a total of $45 on her retirement party? Solve using unit rates.
Answers
The maximum number of guests she can invite is 9.
What is an expression?Expression in maths is defined as the relation of numbers variables and functions by using mathematical signs like addition, subtraction, multiplication, and division.
Given that If Sasha invites three guests, the cost of her retirement party will be $15.
If she can afford to spend $45 the maximum number of the guest will be calculated as:-
3 guests = $15
1 guest = $5
Calculate the maximum guest,
Number of guests = $45 / $5
Number of guests = 9
Therefore, the most visitors she may invite is 9.
To know more about an expression follow
https://brainly.com/question/19672026
#SPJ1
Please show your work, tysm :D
~giving brainliest!~

Answers
Answer:
. 0625
Step-by-step explanation:
1/2^4
or
1/16
just doing half life
How far is the distance from sprinkler head to ?
The distance from sprinkler head B to C is?
.B (-14,-5)
C(-14, 7)
Answers
The distance between the points B and C is 12m
What is the distance between two points?Distance between two points is the length of the line segment that connects the two points in a plane. The formula to find the distance between the two points is usually given by d=√((x2 – x1)² + (y2 – y1)²). This formula is used to find the distance between any two points on a coordinate plane or x-y plane.
for the coordinates B (-14,-5) and C(-14, 7), then x1 = -14 ,x-2= -14 , y1= -5 and y2= 7
therefore d =√((x2 – x1)² + (y2 – y1)²) = √((-14– -14)² + (-5 – 7)²)
d=√((0)² + 12²)
d=√144
d= 12m
therefore the distance between the points B and C is 12m.
learn more about distance between points from
https://brainly.com/question/7243416
#SPJ1
Need help, pls!!!
ty!

Answers
The graph of this function will behave as (b) A graph of this function would slope downward, starting from a price of $100 dollars because the rate of change is less than 0 and the initial value is -10.
The demand function is given by d = 100 - 10p. This means that the quantity demanded (d) decreases as the price (p) increases.
The slope of the demand function is the rate of change of the quantity demanded with respect to the price. In this case, the slope is -10, which is negative. This indicates that as the price increases, the quantity demanded decreases.
The initial value of the demand function is 100, which represents the quantity demanded when the price is zero. This means that the demand function intersects the y-axis at (0, 100).
Therefore, the correct answer is (b) A graph of this function would slope downward, starting from a price of $100 dollars because the rate of change is less than 0 and the initial value is -10.
To learn more about function here:
https://brainly.com/question/12431044
#SPJ1
Please help me with this "Percent Escape Room"
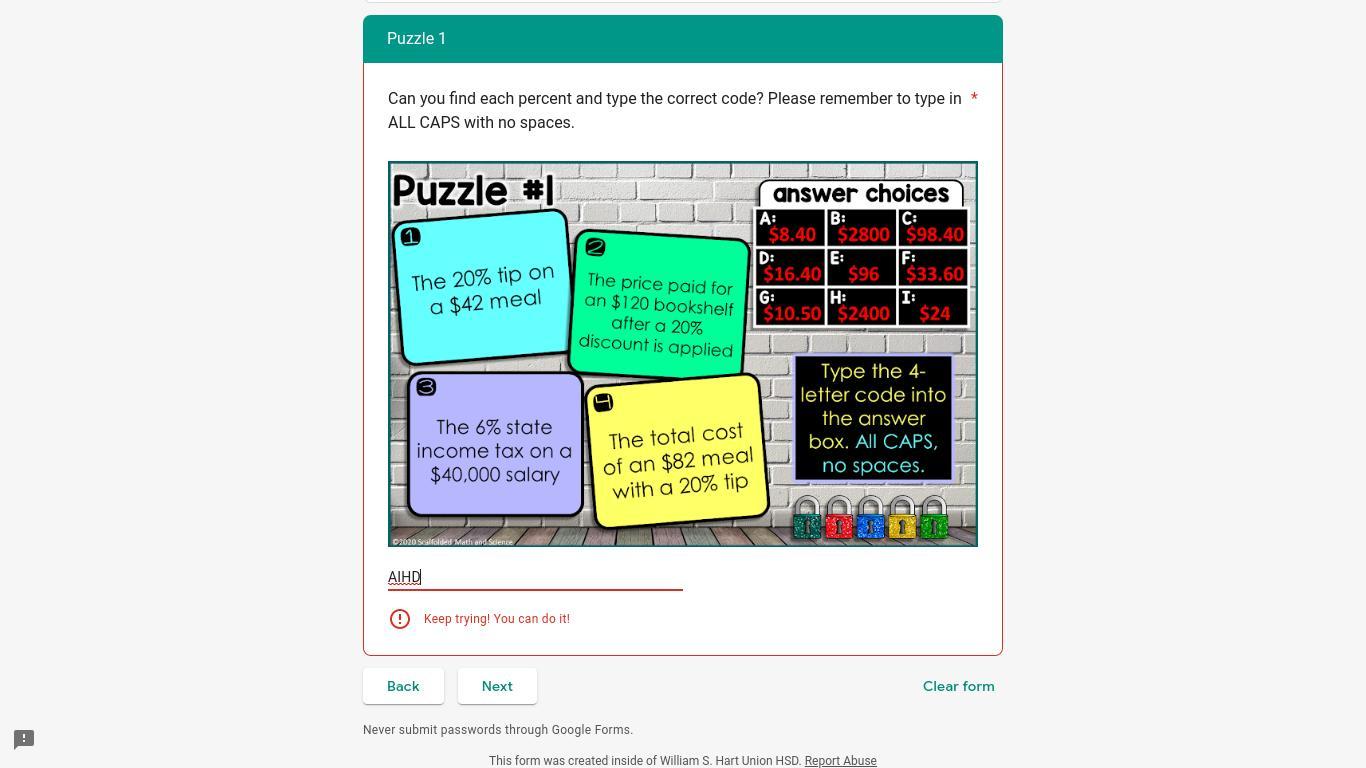
Answers
(1) The 20 Percent tip on a $42 meal will amount to $8.4
(2) The price to be paid for a $120 bookshelf with a 20% discount applied will be $96.
(3) Income Tax on a $40000 salary, with a 6% rate of taxation will be $2400.
(4) The total amount of a $82 meal with a 20% tip will be $98.4.
As per the question statement, we are provided with four different scenarios, and we are required to calculate the following based on the individual scenario:
(1) The amount of 20 Percent tip on a $42 meal
(2) The price to be paid for a $120 bookshelf with a 20% discount applied
(3) The Income Tax amount on a $40000 salary, with a 6% rate of taxation
(4) The total amount of a $82 meal with a 20% tip
Starting to solve with part (1),
20 Percent tip on a $42 meal will be = (20% of 42)
= $[(20/100) * 42]
= $[(2/10) * 42]
= $[(42 * 2)/10]
= $(84/10)
= $8.4
Now solving part (2),
20% discount Amount for a $120 bookshelf = (20% of 120)
= $[(20/100) * 120]
= $(2 * 12)
= $24
And the price to be paid for a $120 bookshelf with the 20% discount applied will be $(120 - 24) = $96
Part (3), Income Tax on a $40000 salary, with a 6% rate of taxation will be = (6% of 40000)
= $[(6/100) * 40000]
= $(6 * 400)
= $2400
And Finally, in part (4),
20% tip amount on a $82 meal = (20% of 82)
= $[(20/100) * 82]
= $[(2/10) * 82]
= $[(82 * 2)/10]
= $(164/10)
= $16.4
Therefore, the total amount of a $82 meal with the 20% tip = $(82 + 16.4)
= $98.4
Percent: In Mathematics, a percentage is a number or a ratio, that is expressed as a fraction of 100, to indicate the amount of a part of something, and is often denoted using the percent sign, "%"To learn more about Percents and Discounts, click on the link below.
brainly.com/question/17063437
#SPJ1
A sales person has a commission of $532 for selling $2800 in merchandise what is the commission rate and what is the answer as a percentage
Answers
Commission amount= sales price* commission percentage
We need to find the commission percentage so we rearrange the equation and plug in the known values:
Commission amount/ sales price = commission percentage
532/2800= commission percentage
Solve the equation: 532/2800= 0.19
0.19 can be converted into percentage as: 0.19*100= 19%
Therefore commission rate= 19%
A pew research Center project on the state of news media showed that the clearest pattern of news audience growth in 2012 came on digital platforms. According to pew research data, 39% of Americans get news online or from a mobile device in a typical day. a. Suppose that you take a sample of 100 Americans. If the population proportion of Americans who get news online or from a mobile device in a typical day is 0.39, what is the probability that fewer than 30% in your sample will get news online or from a mobile device in a typical day? b. Suppose that you take a sample of 400 Americans. If the population proportion of Americans who get news online or from a mobile device in a typical day is 0.39, what is the probability that fewer than 30% in your sample will get news online or from a mobile device in a typical day? c. Discuss the effect of sample size on the sampling distribution of the proportion in general and the effect on the probabilities in (a) and (b).
Answers
Answer:
Step-by-step explanation:
Given that:
the sample proportion p = 0.39
sample size = 100
Then np = 39
Using normal approximation
The sampling distribution from the sample proportion is approximately normal.
Thus, mean \(\mu _{\hat p} = p = 0.39\)
The standard deviation;
\(\sigma = \sqrt{\dfrac{p(1-p)}{n} }\)
\(\sigma = \sqrt{\dfrac{0.39(1-0.39)}{100} }\)
\(\sigma = 0.048\)
The test statistics can be computed as:
\(Z = \dfrac{{\hat _{p}} - \mu_{_ {\hat p}} }{\sigma_{\hat p}}\)
\(Z = \dfrac{0.3 - 0.39 }{0.0488}\)
\(Z = -1. 8 4\)
From the z - tables;
\(P (\hat p \le 0.3 ) = P(z \le -1.84)\)
\(\mathbf{P (\hat p \le 0.3 ) = 0.0329}\)
(b)
Here;
the sample proportion = 0.39
the sample size n = 400
Since np = 400 * 0.39 = 156
Thus, using normal approximation.
From the sample proportion, the sampling distribution is approximate to the mean \(\mu_{\hat p} = p = 0.39\)
the standard deviation \(\sigma_{\hat p} = \sqrt{\dfrac{p(1-p)}{n} }\)
\(\sigma_{\hat p} = \sqrt{\dfrac{0.39 (1-0.39)}{400} }\)
\(\sigma_{\hat p} =0.0244\)
The test statistics can be computed as:
\(Z = \dfrac{{\hat _{p}} - \mu_{_ {\hat p}} }{\sigma_{\hat p}}\)
\(Z = \dfrac{0.3 - 0.39 }{0.0244}\)
\(Z = -3.69\)
From the z - tables;
\(P (\hat p \le 0.3 ) = P(z \le -3.69)\)
\(\mathbf{P (\hat p \le 0.3 ) = 0.0001}\)
(c) The effect of the sample size on the sampling distribution is that:
As sample size builds up, the standard deviation of the sampling distribution decreases.
In addition to that, reduction in the standard deviation resulted in increases in the Z score, and the probability of having a sample proportion that is less than 30% also decreases.
A bowl has 8 green grapes and 15 red grapes. Henry randomly chooses a grape, eats it, and then chooses another grape. What is the probability that both grapes are red? about 39.7% about 41.5% about 42.5% about 44.5%
Answers
Answer:
About 41.5%
Step-by-step explanation:
Given:
A bowl has 8 green grapes and 15 red grapes. Henry randomly chooses a grape, eats it, and then chooses another grape.
To Find:
What is the probability that both grapes are red?
Answer choices:
about 39.7%
about 41.5%
about 42.5%
about 44.5%
Solution:
Since, there are 8 green grapes and 15 red grapes, the total number of grapes is 23 .
As the red grapes are 15..
Thus,
The probability of choosing a red grape the first time is 15/23.
Because out of the total 23 grapes only 15 were red grape.
The probability of choosing the red grape the second time will be 14/22. Because the number of red grapes has already decreased by one and so is the total number of grapes after first choice
Hence, the probability of choosing or eating two red grapes will be :
15/23×14/22
=105/253
=0.415
= 41.5%
Therefore, the probability that both grapes are red is about 41.5%
Kavinsky
if you have 12 rice and you throw it of the velocity of 23 kilometers per hour how many hours does it take to get the velocity of earts speed?
Answers
It would take approximately 1.3 hours for 12 rice to reach the velocity of Earth's orbit at a velocity of 23 km/hr.
What is velocity of Earth's orbit ?The velocity of Earth's orbit around the sun is approximately 30 km/s.
To determine how many hours it takes for 12 rice to reach this velocity, you must use the formula for calculating average speed:
Average Speed = Total Distance/Total Time
Since the total distance is the speed of Earth's orbit (30 km/s) and the total time is the amount of time it takes to reach this speed, then you can solve for the total time by rearranging the equation:
Total Time = Total Distance/Average Speed
Therefore, the total time it takes to reach the velocity of Earth's orbit is:
Total Time = 30 km/s/23 km/hr
= 1.3 hours
It would take approximately 1.3 hours for 12 rice to reach the velocity of Earth's orbit at a velocity of 23 km/hr.
This is because the average speed of the rice is equal to the total distance (30 km/s) divided by the total time (1.3 hours).
For more questions related to orbit
https://brainly.com/question/28106901
#SPJ1
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
How many years will it take an initial investment of $25,000 to triple to $75,000 at an annual rate of 7% compounded continuously
Answers
Answer:
\(t = 15.7\)
Step-by-step explanation:
Given
\(Principal = 25000\) --- P
\(Amount = 75000\) --- A
\(Rate = 7\%\) --- R
Required
Determine the time (t)
Using continuous growth formula:
We have
\(A = Pe^{rt}\)
Convert rate to decimal
\(Rate = 7\%\)
\(r = 0.07\)
Substitute values for A, P and r
\(75000 = 25000 * e^{0.07t}\)
Divide both sides by 25000
\(3 = e^{0.07t}\)
Rewrite the exponential function as logarithmic, we have:
\(ln3 = 0.07t\)
Reorder
\(0.07t = ln3\)
Divide both sides by 0.07
\(t = \frac{ln3}{0.07}\)
\(t = \frac{1.09861228867}{0.07}\)
\(t = 15.69\)
\(t = 15.7\)
Hence, the time is approximately 15.7 years
Scott took out a 72 month
loan for $35,000 to purchase
a new boat. If Scott paid
$8,925 in simple interest,
what was the interest rate?
Answers
$8,925 / ($35,000 * 6 years) = 0.0429 or 4.29%
Therefore, the interest rate on Scott's loan was 4.29%.
The interest rate paid by Scott is 4.25% for the 72 months.
We can determine the simple interest of the given problem by the simple interest formula which is given as :
I=PRT
Where,
I=Interest
P=principal
R=rate in decimal
T=time in years
Converting the given 72 months into years we get time t :
1 year = 12months
72 months / 12months = 6 years
t=6
From the given data
I=8925
P=35000
R=r
T=6
Substituting the above values in the simple interest equation we get:
8925 = 35000*r*6
8925 = 210000*r
divide both sides by 210000
R = 0.0425
Therefore, the interest rate is 4.25%
To learn more about the simple interests :
https://brainly.com/question/25793394
Mrs. Jackson needs to earn $3,000 a month. How much does she need to sell if she earns 15% commission on everything she sells?
Answers
The amount that she needs to sell 15% commission is $2,000.
Given that,
Mrs. Jackson needs to earn $3,000 a month. The commission percentage is 15%.Let us assume the amount be x.Based on the above information, the calculation is as follows:
15% of x = $3,000
x = $2,000
Learn more: brainly.com/question/17429689
Mrs. Jackson needs to sell a total of $20,000 worth of products to earn $3,000 a month with a 15% commission on everything she sells.
Given that,
Mrs. Jackson needs to earn $3,000 a month.
The commission percentage is 15%.
Let us assume the amount be x.
To calculate how much Mrs. Jackson needs to sell to earn $3,000 a month, we can use the formula for commission-based earnings:
Earnings = Commission Rate × Sales
We know that Mrs. Jackson earns a 15% commission on everything she sells, and her goal is to earn $3,000 a month.
Let x be the total sales amount she needs to achieve her goal.
Earnings = 0.15x
According to the problem, she needs to earn $3,000, so we can set up the equation:
0.15x = $3,000
Now, to find x, we need to isolate it on one side of the equation. We can do that by dividing both sides by 0.15:
x = $3,000 / 0.15
x = $20,000
So, Mrs. Jackson needs to sell a total of $20,000 worth of products to earn $3,000 a month with a 15% commission on everything she sells.
To learn more on percentage click:
brainly.com/question/13450942
#SPJ3
Find the solution of the differential equation that satisfies the given initial condition. dy/dx=x/y , y(0)=-1
Answers
Separating variables, we have
\(\dfrac{dy}{dx} = \dfrac xy \implies y\,dy = x\,dx\)
Integrate both sides.
\(\displaystyle \int y\,dy = \int x\,dx\)
\(\dfrac12 y^2 = \dfrac12 x^2 + C\)
Given that \(y(0)=-1\), we find
\(\dfrac12 (-1)^2 = \dfrac12 0^2 + C \implies C = \dfrac12\)
Then the particular solution is
\(\dfrac12 y^2 = \dfrac12 x^2 + \dfrac12\)
\(y^2 = x^2 + 1\)
\(y = \pm\sqrt{x^2 + 1}\)
and because \(y(0)=-1\), we take the negative solution to accommodate this initial value.
\(\boxed{y(x) = -\sqrt{x^2+1}}\)
39. From the top of a vertical cliff 50 meters high, the angles of depression of an object that is levelled with
the base of the cliff is 30°. How far is the object from the base of the cliff?
A. 50 meters
B. 50-√3 meters
C. 100 meters
D. 100-√3 meters
40. What expression is used to answer: "A 4-m tall man stands on horizontal ground 43 m from a tree.
The angle of depression from the top of the tree to his eyes is 22°. Estimate the height of the tree."
A. sin 22
B. cos 22
C. tan 22
D. cot 22
41. From the top of the building of a food chain, the angle of depression from where Miguel stands is
45°. If the building is 12 meters high, how far is he from it?
A. 11 meters
B. 12 meters
C. 13 meters
D. 14 meters
42. A plane, at an altitude of 3,000 feet, observes the airport at an angle of 27°. What is the
horizontal distance between the plane and the airport to the nearest foot?
A. 3,000 feet
B. 4,000 feet
C. 5,000 feet
D. 6,000 feet
43. An escalator has an angle of elevation of 10° and a vertical rise of 6 m. Find the length of the
escalator.
C. 34.55 m
D. 36 m
A. 6,09 m
B. 34,03 m
Answers
Answer: cos4
Step-by-step explanation: 50 meters
B. 50-√3 meters
C. 100 meters
D. 100-√3 meters
40. What expression is used to answer: "A 4-m tall man stands on horizontal ground 43 m from a tree.
The angle of depression from the top of the tree to his eyes is 22°. Estimate the height of the tree."
A. sin 22
B. cos 22
C. tan 22
D. cot 22
WILL MARK BRAINLYIST
Answers
Answer:
what's the question
Step-by-step explanation:
lol but u could mark me brainlyist
Answer:
.....................................
Step-by-step explanation:
ALGEBRA please put a very small explanation to the awnser


Answers
Certainly! The problem can be solved using the Pythagorean theorem,
which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In this case, the ladder acts as the hypotenuse, and we need to find the length of the vertical side (height) it reaches up the wall.
The ladder forms the hypotenuse, and its length is given as 12 meters. The distance from the foot of the ladder to the base of the wall represents one side of the triangle, which is 4.5 meters.
By substituting the given values into the Pythagorean theorem equation: (12m)^2 = h^2 + (4.5m)^2, we can solve for the unknown height 'h'.
Squaring 12m gives us 144m^2, and squaring 4.5m yields 20.25m^2. By subtracting 20.25m^2 from both sides of the equation, we isolate 'h^2'.
We then take the square root of both sides to find 'h'. The square root of 123.75m^2 is approximately 11.12m.
Therefore, the ladder reaches a height of approximately 11.12 meters up the wall.
For more questions Pythagorean theorem:
https://brainly.com/question/343682
#SPJ8
Solve the following equation. Then place the correct number in the box provided. 3x + 1 = 2x + 12
Answers
Answer:
x = 11
Step-by-step explanation:
3x+1 = 2x+12 (subtract 2x from both sides)
x+1 = 12 (subtract 1 from both sides)
x = 11
So x is equal to 11
find the composition and simplify your answer as much as possible. Write the domain using interval notation.

Answers
The composition f∘g is given by (13) / (x - 13).
The domain of the composition is all real numbers except for x = 13, which can be represented in interval notation as (-∞, 13) U (13, ∞).
To find the composition f∘g, we need to substitute g(x) into f(x) in the following way:
f(g(x)) = f(13/x) = (13/x) / ((13/x) - 1)
To simplify this expression, we can multiply both the numerator and denominator by x, which gives us:
f(g(x)) = (13) / (x - 13)
The domain of f(g(x)) is restricted by the domain of g(x), which is all real numbers except for x = 0. Therefore, the domain of f(g(x)) is the set of all real numbers except for x = 13.
Using interval notation, we can write the domain of f(g(x)) as:
(-∞, 13) U (13, ∞)
To learn more about composition click on,
https://brainly.com/question/29059805
#SPJ1
unfortunately, the set up of these problems is very confusing for me because they keep altering and changing per problem

Answers
Answer:
2292.03
Step-by-step explanation:
Start with the formula for continuously compounded interest.
Then substitute all given values in the formula.
Finally, solve for the only variable remaining.
\( A = Pe^{rt} \)
A = future value = $5000
P = principal (deposited amount) = unknown
r = 6.5% = 0.065
t = time = 12 years
\( 5000 = Pe^{0.065 \times 12} \)
\( 5000 = Pe^{0.78} \)
\(5000 = P \times 2.18147\)
\( P = \dfrac{5000}{2.18147} \)
\( P = 2292.03 \)
Answer: $2292.03
Answer:
P = $2366.91
(maybe try answering without a comma)
Step-by-step explanation:
The formula for continuous compounding is:
A = Pe^(rt)
Where:
A = final amount
P = principal amount (initial deposit)
e = Euler's number (approximately 2.71828)
r = annual interest rate (as a decimal)
t = time (in years)
We are given:
r = 6.5% = 0.065 (annual interest rate)
t = 12 years
A = $5000 (final amount)
So we can rearrange the formula to solve for P:
P = A / e^(rt)
Substituting the values:
P = 5000 / e^(0.065*12)
P = $2366.91 (rounded to the nearest cent)
Therefore, you would need to deposit $2366.91 in an account with a 6.5% interest rate, compounded continuously, to have $5000 in your account 12 years later.