Answers
We have been given image of a circle. We are asked to find the measure of angle WTV.
We know that measure of an inscribed angle is half the measure of intercepted arc.
We can see that angle WTV is inscribed angle to arc WV. So measure of angle WTV will be half the measure of arc WV.
\(\angle WTV=\frac{1}{2}\widehat{WV}\)
\(\angle WTV=\frac{1}{2}\cdot 90^{\circ}\)
\(\angle WTV=45^{\circ}\)
Therefore, the measure of angle WTV is 45 degrees and 2nd option is the correct choice.
Related Questions
Rewrite the following equation in slope-intercept form. y - 10 = 4(x - 3)
Answers
Answer:
y=4x-2
Step-by-step explanation:
Is x+y is an algebraic expression?
A. Yes
B. No
C. Cannot be identified
D. None of these
Answers
Answer:
A. Yes
Step-by-step explanation:
It depends on the definition of "algebraic expression", and especially the meaning of "algebraic" you take to use in your context. If you talk from a high-school perspective, then yes, x+y−π is an algebraic expression, because... well, it looks like algebra and has algebraic-looking characters.
Answer:
A. Yes
Step-by-step explanation:
Yeah, x+y is an algebraic expression. This statement is correct. So, option (A) is the correct answer.
ad←→ is tangent to circle b at point c. the measure of ∠abc is 40º. what is the measure of ∠bac? responses 40º 40º 50º 50º 90º 90º 180º
Answers
The value of ∠BAC is 50°. Hence, the correct option is 50º.Given, AD is tangent to circle B at point C. ∠ABC = 40°.We need to find the value of ∠BAC.Therefore, let's solve this problem below:As AD is tangent to circle B at point C, it forms a right angle with the radius of circle B at C.
∴ ∠ACB = 90°Also, ∠ABC is an external angle to triangle ABC. Therefore,∠ABC = ∠ACB + ∠BAC = 90° + ∠BACNow, putting the value of ∠ABC from the given information, we get,40° = 90° + ∠BAC40° - 90° = ∠BAC-50° = ∠BAC
Therefore, the value of ∠BAC is 50°. Hence, the correct option is 50º.
To know more about tangent visit:
https://brainly.com/question/10053881
#SPJ11
The picture below shows the graph of which inequality?

Answers
The graph shows the inequality x² ≤ 16
How find the inequality for the graph?An inequality is a relationship that makes a non-equal comparison between two numbers or other mathematical expressions e.g. 2x > 4.
Inequalities are often used to describe conditions or constraints in real-world problems.
You will notice that the values represented in the graph ranges from -4 to 4. Thus, solving x² ≤ 16 will produce these values. That is:
x² ≤ 16
x ≤ ±√16
x ≤ ±4
x ≤ -4 or x ≤ 4
Learn more about inequality on:
brainly.com/question/25275758
#SPJ1
A large university accepts 70% of the students who apply. Of the students the university accepts,25% actually enroll. If 20,000 students apply, how many enroll?
Answers
The number of students that enrolled = 3,500 students.
What is enrollment?This is defined as the intake of individuals into an organism or students into an institution through adherence to specific orders given by the administrative department of the organisation.
The number of students that apply= 20,000 students
The percentage of students that are accepted= 70% of 20,000
That is, 70/100× 20,000
= 1400000/100
= 14,000 students.
The quantity of students that actually enroll = 25% of 14,000
That is, 25/100× 14000
= 350000/100
= 3,500 students.
Learn more about percentage here:
https://brainly.com/question/24304697
#SPJ1
from a point on a river, two boats are driven in opposite directions, one at 10 miles per hour and the other at 14 miles per hour. in how many hours will they be 120 miles apart?
Answers
The two boats will be 120 miles apart in five hours.
We need to find the time at which the boats will be 120 miles apart from each other.
It has been given that the total distance is 120 miles.
Now, let's take up the following assumptions in order to arrive at the time taken by two boats to cover the requisite distance:-
Let x= distance traveled by boat 1 at 10 miles per hour.
Let y= distance traveled by boat 2 at 14 miles per hour.
Thus, x+y=120(given)------(i) [That is, distance travelled by boat 1+ Distance travelled by boat 2= Total Distance]
Let t denote the time factor,
then, Boat 1 will travel x miles in T hours, and the Boat 2 will travel y miles in T hours.
We know, Distance= Rate * Time
Thus, we can say, x= 10*T---------------(ii)
y=14*T-----------------(iii)
Adding equations ii and iii, we get
x+y=24T----------------(iv)
Now, subtracting equation (iv) from (i), we get
24T-120=0
24T= 120
thus, we get t=5
Hence, the time taken by two boats, to be 120 miles apart is five hours.
To know more about equations:
https://brainly.com/question/10777820
#SPJ4
Use the quadratic formula to find both solutions to the quadratic equation
given below.
3x2 - 5x-1=0
A. X= 5 - (gcf)13/6
B. X= 5 - (gcf)13/6
c. X= 5+ (gcf)13/6
D. X= -5 + (gcf)13/6
E. X= 5+ (gcf)37/6
F. x= 5 - (gcf)37/6
Answers
Answer:
E. X= 5+ (gcf)37/6
F. x= 5 - (gcf)37/6
Step-by-step explanation:
put in calculator MOD 5 3
write the values: -
a= 3 b= -5 c= -1
Two years ago, Estelle reserved 24 books in 4 months. Then last year, Estelle reserved books in 36 months. Finally, this year, Estelle reserved 18 books in 3 months. Write this proportional relationship as an equation in the form , where is the unit rate between books and months.
Answers
Answer: To write the proportional relationship between books and months, we can use the formula:
unit rate = (total books) / (total months)
Let's calculate the total books and months for Estelle's reservations:
Two years ago: 24 books in 4 months
Last year: unknown number of books in 36 months
This year: 18 books in 3 months
To find the total number of books for last year, we can use a proportion:
24 books / 4 months = x books / 36 months
Cross-multiplying, we get:
24 * 36 = 4 * x
x = 24 * 9
x = 216
So Estelle reserved 216 books in 36 months last year.
Now we can calculate the unit rate:
unit rate = (total books) / (total months)
unit rate = (24 + 216 + 18) / (4 + 36 + 3)
unit rate = 258 / 43
unit rate = 6
Therefore, the proportional relationship between books and months is:
books = 6 * months
Step-by-step explanation:
According to the synthetic division below, which of the following statements
are true?
Check all that apply.
Answers
The question is not complete, so i have attached it.
Answer:
Options A, B & E are correct
Step-by-step explanation:
In the synthetic division attached, we see that:
: 2 , -2 & -12 are the coefficient of the dividend of the function 2x² - 2x - 12
: The divisor is 3
Thus;
x = 3 is a root of f(x) = 2x² - 2x - 12
Thus, (x - 3) is a factor of the dividend which is the function f(x) = 2x² - 2x - 12
- Now, from the attached image, the coefficients of the quotient are 2 , 4
- The quotient will be 1 degree less than the dividend since it was divided by the factor (x - 3)
The degree of the dividend will be 2 since it contains x²
Thus, the degree of the quotient will be 1
Therefore, the quotient in factor form is (2x + 4)
Looking at the given statements in the options;
- Option A is true, because we have established earlier that 3 is a root of f(x) = 2x² - 2x - 12
- Option B is true because we have established that (x - 3) is a factor of 2x² - 2x - 12
- Option C is not true because the factor is (x + 3) and not (x - 3)
-Option D is not true because the root is 3 and not -3
- Option E is true because we have established that quotient as a factor is: (2x + 4)
Thus, the correct options are A , B , E

If f (x) = x^2 + 3, evaluate f (-4).
=
A) -5
B) 19
C
11
D) -13
Answers
Answer: B) 19
Step-by-step explanation:
To solve this problem, simply plug in -4 for x:
\(f(x)=x^{2} +3\\f(x)=(-4)^{2} +3\\f(x)=16+3\\f(x)=19\)
Hope it helps :) and let me know if you want me to elaborate/explain further
Answer:
D. -13
Step-by-step explanation:
If you substitute -4 in for x you get -4^2+3, so when you simplify you get -16+3 which equals -13.
f(x)=x^2+3
f(-4)= -4^2+3
f(-4)= -16+3
f(-4)= -13
2x2 + 6x - 25 = 0
Can someone help me solve this?
Answers
Answer:
Hope this helped you a little
Step-by-step explanation:

If the following jobs are sequenced according to the SLACK rule then job A would be completed on day (assume zero for today's date)
Job - Processing Time (days) - Due Date
A 8 12
B 6 15
C 11 17
D 7 10
E 3 8
Select one: A. 7. B. 15. C. 8. D. 12.
Answers
If the jobs are sequenced according to the SLACK rule, Job A would be completed on day 12.
The SLACK rule involves calculating the slack time for each job, which is the difference between the due date and the completion time. The job with the least slack time is prioritized and scheduled first. In this case, the due dates for the jobs are as follows: Job A (12), Job B (15), Job C (17), Job D (10), and Job E (8).
Job A has a processing time of 8 days and a due date of 12, so the slack time is 12 - 8 = 4 days. Since Job A has the least slack time among all the jobs, it would be completed on day 12. Therefore, the answer is D. 12.
Learn more about slack here: brainly.com/question/29352983
#SPJ11
Suppose P, is the terminal point on the unit circle and is determined by the real number t, and P, E II. P, has y-coordinate. Find each of the following (i) sin (t+6x) (ii) cost (iii) tan (t + r)
Answers
(i) sin(t + 6π) = sin(t). (ii) cos(t). (iii) tan(t + π). (i) Since the unit circle has a period of 2π, adding a multiple of 2π to an angle does not change the sine function. Therefore, sin(t + 6π) is equal to sin(t)
(ii) The y-coordinate of a point on the unit circle represents the value of the cosine function. So, the y-coordinate of P represents cos(t).
(iii) The tangent function is defined as the ratio of the sine and cosine functions. Therefore, tan(t + π) = sin(t + π) / cos(t + π). Using the periodicity of sine and cosine, we have sin(t + π) = -sin(t) and cos(t + π) = -cos(t). Thus, tan(t + π) = -sin(t) / -cos(t) = sin(t) / cos(t) = tan(t).
Therefore:
(i) sin(t + 6π) = sin(t)
(ii) cos(t)
(iii) tan(t + π)
Learn more about trigonometric functions here: brainly.com/question/25618616
#SPJ11
any one can solve this
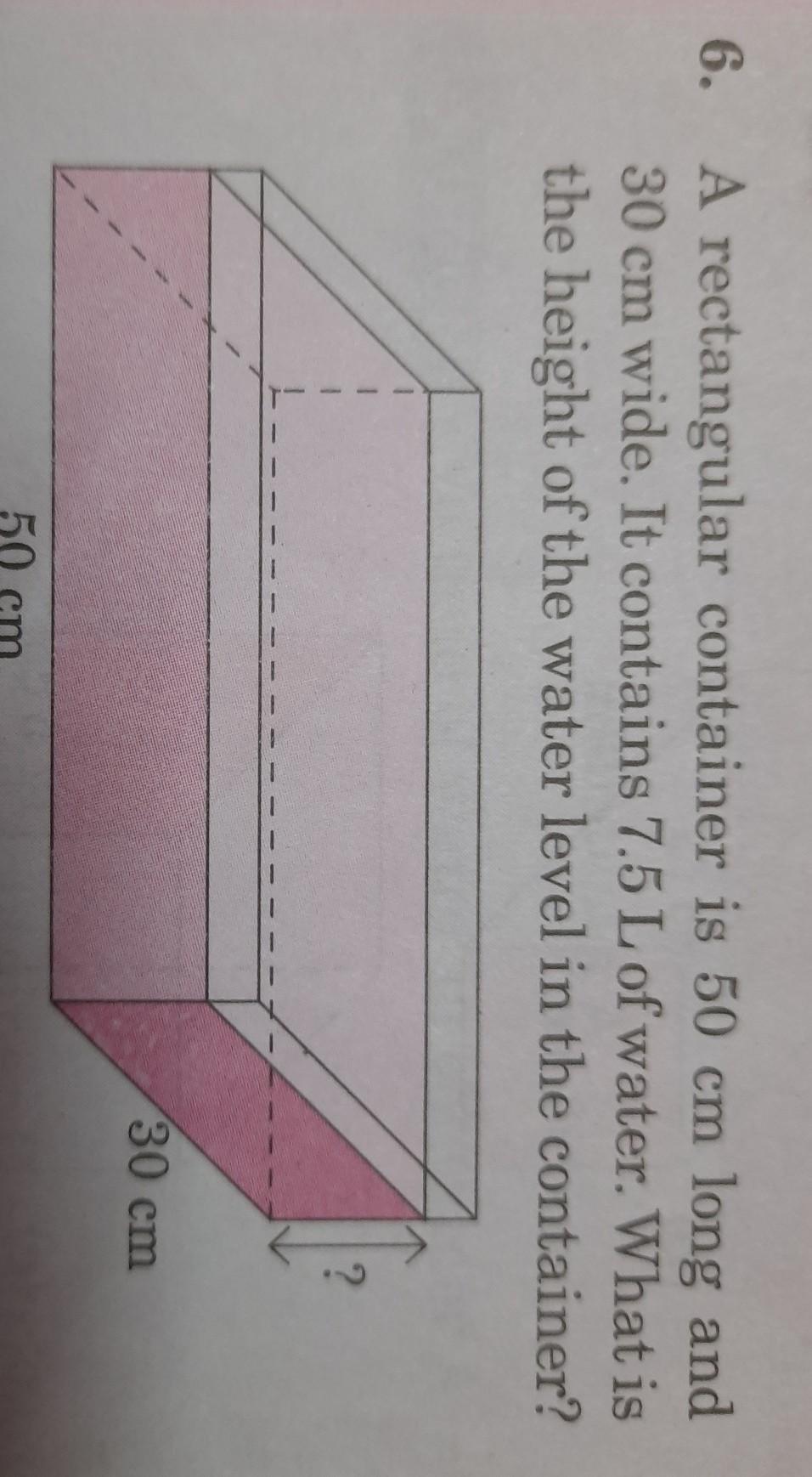
Answers
Answer:
The height of water in the container is 5 cm
Step-by-step explanation:
Here, we want to calculate the height of the water in the container
Mathematically, the volume is :
50 * 30 * h = 1500h cm^3
Also, 7.5 L = 7500 cm^3 = 7.5 L
Let the height be h
1500h = 7500
h = 7500/1500
h = 5 cm
Score on last try: 0.5 of 1 pts. See Details for more. Get a similar question You can retry this question below Find the absolute extrema of the function f(x, y) = 2x² + 2y² + x + y − 1 on the domain defined by x² + y² ≤ 9. Round answers to 3 decimals or more. Absolute Maximum: 21.243 Absolute Minimum: 12.757 X
Answers
The absolute maximum value of the function f(x, y) = 2x² + 2y² + x + y - 1 on the domain x² + y² ≤ 9 is 21.243, and the absolute minimum value is 12.757.
To find the absolute extrema of the given function on the given domain, we can use the method of Lagrange multipliers. First, we define the objective function as f(x, y) = 2x² + 2y² + x + y - 1, and the constraint function as g(x, y) = x² + y² - 9.
Next, we calculate the partial derivatives of the objective function with respect to x and y, as well as the partial derivatives of the constraint function with respect to x and y. Setting up the Lagrange equations, we have:
∇f(x, y) = λ∇g(x, y)
where ∇ represents the gradient operator and λ is the Lagrange multiplier. Solving these equations simultaneously, we obtain values for x, y, and λ.
By substituting the obtained values of x and y into the objective function f(x, y), we can calculate the corresponding function values. The maximum value among these function values represents the absolute maximum, and the minimum value represents the absolute minimum on the given domain.
Rounding the results to three decimal places, we find that the absolute maximum is 21.243, and the absolute minimum is 12.757. These values indicate the highest and lowest points, respectively, that the function achieves on the given domain.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
The probability density function of the length of a cutting blade is f(x) = 1.25 for 74.6 < x < 75.4 millimeters. Determine the following: (a) P(X < 74.8) (b) P(X < 74.8 or X > 75.2) (c) If the specifications of this process are from 74.7 to 75.3 millimeters, what proportion of blades meets specifications?
Answers
First, let me explain a few terms. Density refers to the amount of something in a given space, while function refers to a relationship between two or more variables. In this case, the probability density function is a function that describes the likelihood of a cutting blade having a certain length. Blades, of course, refer to the objects being measured.
Now, let's move on to the questions.
(a) P(X < 74.8) means the probability that a blade's length is less than 74.8 millimeters. To find this probability, we need to integrate the probability density function from 74.6 to 74.8:
P(X < 74.8) = ∫f(x)dx from 74.6 to 74.8
= ∫1.25dx from 74.6 to 74.8
= 1.25(74.8 - 74.6)
= 0.25
Therefore, the probability of a blade's length being less than 74.8 millimeters is 0.25.
(b) P(X < 74.8 or X > 75.2) means the probability that a blade's length is either less than 74.8 millimeters or greater than 75.2 millimeters. To find this probability, we need to add up the probabilities of these two events:
P(X < 74.8 or X > 75.2) = P(X < 74.8) + P(X > 75.2)
= 0.25 + ∫f(x)dx from 75.2 to 75.4
= 0.25 + 1.25(75.4 - 75.2)
= 0.5
Therefore, the probability of a blade's length being either less than 74.8 millimeters or greater than 75.2 millimeters is 0.5.
(c) If the specifications of this process are from 74.7 to 75.3 millimeters, we need to find the proportion of blades that meet these specifications. This is equivalent to finding the probability that a blade's length is between 74.7 and 75.3 millimeters. To find this probability, we need to integrate the probability density function from 74.7 to 75.3:
Proportion of blades meeting specifications = ∫f(x)dx from 74.7 to 75.3
= 1.25(75.3 - 74.7)
= 0.75
Therefore, the proportion of blades that meet specifications is 0.75, or 75%.
(a) To find P(X < 74.8), we need to calculate the area under the probability density function (PDF) from 74.6 to 74.8 millimeters. Since f(x) = 1.25 is a constant, we can find the area by multiplying the length of the interval by the constant value of the function:
P(X < 74.8) = 1.25 * (74.8 - 74.6) = 1.25 * 0.2 = 0.25
(b) To find P(X < 74.8 or X > 75.2), we need to calculate the area under the PDF from 74.6 to 74.8 and from 75.2 to 75.4 millimeters. The total probability is the sum of the probabilities for each interval:
P(X < 74.8 or X > 75.2) = 1.25 * (74.8 - 74.6) + 1.25 * (75.4 - 75.2) = 1.25 * 0.2 + 1.25 * 0.2 = 0.25 + 0.25 = 0.5
(c) If the specifications are from 74.7 to 75.3 millimeters, we need to calculate the area under the PDF from 74.7 to 75.3 millimeters:
Proportion of blades meeting specifications = 1.25 * (75.3 - 74.7) = 1.25 * 0.6 = 0.75
So, 75% of the blades meet the specifications.
Visit here to learn more about Probability:
brainly.com/question/24756209
#SPJ11
write an algebraic equation that matches the values shown in the table. explain how you solved the problem. x y 1 14 2 23 3 32 4 41
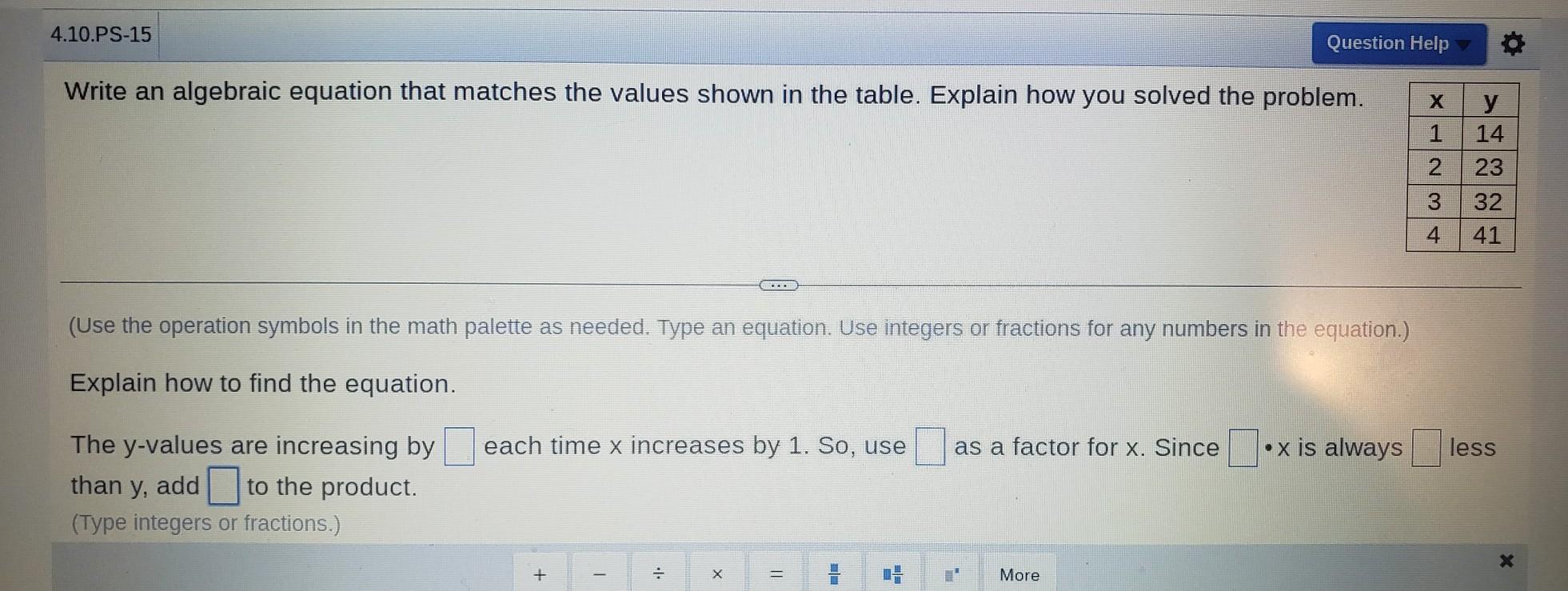
Answers
Standard formula of linear equation is: y = mx+b
What is algebraic equation?
In mathematics, an algebraic or polynomial equation is an equation of the form P=0, where P is a polynomial with coefficients in some field (often a field of rational numbers). For many authors, the term algebraic equation refers only to univariate equations, i.e. polynomials involving only one variable. A polynomial, on the other hand, may contain multiple variables. For multiple variables (multivariate), the term polynomial is usually preferred over algebraic equations.
Some, but not all, polynomials with rational coefficients have solutions that are algebraic expressions that can be found using a finite number of operations involving only the same kind of coefficients (that is, they can be solved algebraically I can). This can be done for any equation of degree 1, 2, 3, or 4. But for 5th grade and above, it can only be done for some equations, not all. Much work has been devoted to efficiently computing exact approximations to real or complex solutions to univariate algebraic equations (see Root Finding Algorithms).
Therefore, Standard formula of linear equation is: y = mx+b
To know more about algebraic equation, visit:
https://brainly.com/question/4344214
#SPJ1
you can rent time on computers at the local copy center for a $10 setup charge and an additional $2 for every 5 minutes. how much time can you rent for $25?
Answers
You can rent time on computers at the local copy center for 35 minutes with $25.
To find out how much time you can rent for $25 at the local copy center, follow these steps:
1. Subtract the $10 setup charge from the total amount you have: $25 - $10 = $15.
2. Now you have $15 left for renting time on the computers. Since it costs $2 for every 5 minutes, you need to find out how many 5-minute increments can be covered by $15.
3. Divide the remaining amount by the cost per 5-minute increment: $15 / $2 = 7.5. Since you can't have half an increment, round down to 7.
4. Multiply the number of 5-minute increments by the time per increment: 7 * 5 = 35 minutes.
So, you can rent time on computers at the local copy center for 35 minutes with $25.
To learn more about rent
https://brainly.com/question/28452806
#SPJ11
Suppose you are interested in signing up for a cell phone plan. There are two plans available.
Plan 1
$95 start-up fees
$20 per month after the 1st month
Plan 2
No start-up fee
$35 per month after the first month
Answers
Answer:
The first plan is better
Step-by-step explanation:
The first plan is better because after you do a yearly subscription you only have to pay 335 dollars. The second plan has to make you pay 420 dollars for a yearly subscription. Choose the 1st plan for a cheaper cost.
El ruedo de la plaza de toros "Las Ventas", de
Madrid, España mide 61. 5 metros de diámetro,
mientras que el de la Plaza "México", tiene una
circunferencia de 135. 02 metros. ¿Cuál de los dos
ruedos es más grande?
Answers
Answer:
mention any one contribution of maiti nepal
Let P(t) denote the population of bacteria in a
Petri disht hours after bacteria are introduced to the environment
of the Petri dish. Suppose that the initial population of bacteria
is known to be 5000, and that the bacteria population doubles
every 6 hours. Assume that the population can grow indefinitely.
Give a formula for P(t).
Answers
well, if the population is doubling from whatever they happen to be, so that means the growth rate is 100%, so if they're hmmm "g", then later they become "2g", or doubled, and the later becomes "4g" and so on, so the rate is simply 100%, because "g" plus "g" is just 2g, and "2g" plus "2g" is just 4g and so on, anyhow
\(\textit{Periodic/Cyclical Exponential Growth} \\\\ A=P(1 + r)^{\frac{t}{c}}\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{initial amount}\dotfill &5000\\ r=rate\to 100\%\to \frac{100}{100}\dotfill &1\\ t=hours\\ c=period\to &6 \end{cases} \\\\\\ A=5000(1 + 1)^{\frac{t}{6}}\implies A=5000(2)^{\frac{t}{6}}\implies {\Large \begin{array}{llll} P(t)=5000(2)^{\frac{t}{6}} \end{array}}\)
Larry decides to walk around the block of his neighborhood one afternoon. The neighborhood is in the shape of a square and each street is 2 miles long. What is the area of the neighborhood?
Answers
Answer:
4miles²Step-by-step explanation:
Area of a square = Length * Length
If the neighborhood is in the shape of a square and each street is 2 miles long, then the length of the square is 2 miles.
Area of the neighborhood can simply be calculated using the area for finding the area of a square.
Area of the neighborhood = 2miles * 2miles
Area of the neighborhood = 4miles²
suppose v1,v2,v3 is an orthogonal set of vectors in r5. let w be a vector in span(v1,v2,v3) such that v1⋅v1=6,v2⋅v2=18,v3⋅v3=25, w⋅v1=−6,w⋅v2=−90,w⋅v3=−75,
Answers
According to the information, we can express the vector w as a linear combination of v1, v2, and v3 like this: w = -v1 - 5v2 - 3v3
How to express the vector w as a linear combination?We can express the vector w as a linear combination of v1, v2, and v3. Let's say:
w = c1 v1 + c2 v2 + c3 v3
We can find the values of c1, c2, and c3 using the dot product properties of orthogonal vectors. Since v1, v2, and v3 are orthogonal:
w ⋅ v1 = (c1 v1 + c2 v2 + c3 v3) ⋅ v1 = c1 (v1 ⋅ v1) = 6c1
w ⋅ v2 = (c1 v1 + c2 v2 + c3 v3) ⋅ v2 = c2 (v2 ⋅ v2) = 18c2
w ⋅ v3 = (c1 v1 + c2 v2 + c3 v3) ⋅ v3 = c3 (v3 ⋅ v3) = 25c3
Using the given values, we can set up a system of equations:
-6 = 6c1 + 0c2 + 0c3
-90 = 0c1 + 18c2 + 0c3
-75 = 0c1 + 0c2 + 25c3
Solving for c1, c2, and c3, we get:
c1 = -1
c2 = -5
c3 = -3
Therefore, we have:
w = -v1 - 5v2 - 3v3
Note: The solution is not unique, as any linear combination of v1, v2, and v3 that satisfies the given dot product conditions would work.
Learn more about vectors in: https://brainly.com/question/13322477
#SPJ1
Please help me! thank you
Suppose an object is thrown upward with initial velocity of 48 feet per second from a high of 120 feet. The height of the object t seconds after it is thrown is given by h(t)=-16t^2+48t+120. Find the average velocity from t=2 to t=4.
Type your answer as a number with no units.
Answers
The average velocity from t = 2s to t = 4s would be - 48 ft/s.
What are algebraic expressions?In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context.
Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.
Given is that an object is thrown upward with initial velocity of 48 feet per second from a high of 120 feet. The height of the object t seconds after it is thrown is given by h(t) = - 16t² + 48t + 120.
Average velocity
Average rate of change of velocity with time is called average velocity. Mathematically -
v{avg.} = Δx/Δt .... Eq { 1 }
Δx = x(4) - x(2)
Δx = - 16(4)² + 48(4) + 120 - {- 16(2)² + 48(2) + 120}
Δx = - 96
Δt = 4 - 2 = 2
So -
v{avg.} = Δx/Δt = -96/2 = - 48 ft/s
Therefore, the average velocity from t = 2s to t = 4s would be - 48 ft/s.
To solve more questions on functions, visit the link below-
brainly.com/question/17613163
#SPJ1
uppose that a certain data set contains the variable HEIGHT (giving a person's height) and the variable GENDER (coded O=female, 1=male). Then the y-intercept of the regression equation predicting HEIGHT from GENDER is given by: Select one: a. how much shorter females are than males, on average. b. how much taller males are than females, on average. c. the average height of females in the data set. d. the average height of males in the data set. e. the proportion of females in the data set. f. the proportion of males in the data set. g. it is not appropriate to interpret the y-intercept in this case.
Answers
The data set contains the variable height (giving a person's height) and the variable gender (coded O=female, 1=male). Then the y-intercept of the regression equation predicting height from gender is given by: option c) the average height of females in the data set.
The y- intercept of a direct retrogression relationship represents the value of one variable when the value of the other is zero. Non-linear retrogression models also live, but are far more complex. Retrogression analysis is a important tool for uncovering the associations between variables observed in data, but can not fluently indicate occasion. The data set contains the variable height (giving a person's height) and the variable gender (enciphered O = womanish, 1 = manly). also the y- intercept of the retrogression equation prognosticating height from gender is given by option c) the average height of ladies in the data set.
To learn more about y-intercept, click here:
brainly.com/question/14180189
#SPJ4
How I can answer this question, NO LINKS, If you answer correctly I will give u brainliest!

Answers
Answer for 2. B
Answer for 3. B
Is 0.343434 an irrational or rational?
Answers
Answer:
irrational
Step-by-step explanation:
a rational number is always a whole number
Guide
A chemist mixes Chemical A and Chemical B to make a solution. She uses the same ratio of chemicals for each batch she
makes.
Drag numbers to complete the table.
?
4
6
12
Chemical A (ML) Chemical B (mL)
3
36
48
84
36
96
108
132
168
7
9
Answers
When chemist mixes Chemical A and Chemical B to make a solution
Part A
When the quantity of chemical B = 48 ml, then the quantity of chemical A = 4 ml
Part B
When the quantity of chemical A = 9 ml, then the quantity of chemical B = 108 ml
A chemist mixes Chemical A and Chemical B to make a solution
She uses the same ratio of chemicals for each batch
The solution A and B are in linear relationship
y = kx
Where y is the quantity of chemical A
x is the quantity of chemical B
k is the constant
Substitute the values in the table and find k
36 = k × 3
k = 36 /3
k = 12
Part A
When chemical B = 48 ml
48 = 12 × x
x = 48 / 12
x = 4 ml
Part B
When chemical A = 9 ml
y = 12 × 9
y = 108 ml
Therefore, when Chemical B = 48 ml, chemical B is 4ml . When chemical A = 9 ml, Chemical B = 108 ml
Learn more about ratio here
brainly.com/question/13637951
#SPJ4
Please help with trig problem very confusing.

Answers
Answer:
this so you just divide the numbers and should get answers
(Slope-Intercept to Standard Form)
y=6/5 x
How would I work this out?
Answers
Since 6 represents x and 5 represents y, you have to write it as 6x and 5y. And it’s going to equal zero since there is no y-intercept.
