What is the area of a circle with the radius of 11.5 meters? ill give brainliest
Answers
Answer:
415.265 m²
Step-by-step explanation:
A=π r²
π*132.25
Answer:
415.48 m²
The area would be 415.48 square meters
Related Questions
PLEASE HELP ME!!!! HOMEWORK DUE IN 30 MIN!!!!!!

Answers
Answer:
b is 10.5 c is 11
Step-by-step explanation:
9+1.5
10.5
3(5)-4
15-4
11
please help me!!!!!!!!!!!!!

Answers
Answer:
I'm not positive on this but I think the answer might be C 27 sin (39)/ sin (51)
Step-by-step explanation:
Consider the following hypothesis test.
H0: μ ≤ 12
Ha: μ > 12
A sample of 25 provided a sample mean
x = 14
and a sample standard deviation
s = 4.54.
(a)
Compute the value of the test statistic. (Round your answer to three decimal places.)
(b)
Use the t distribution table to compute a range for the p-value.
p-value > 0.2000.100 < p-value < 0.200 0.050 < p-value < 0.1000.025 < p-value < 0.0500.010 < p-value < 0.025p-value < 0.010
(c)
At
α = 0.05,
what is your conclusion?
Do not reject H0. There is insufficient evidence to conclude that μ > 12.Do not reject H0. There is sufficient evidence to conclude that μ > 12. Reject H0. There is insufficient evidence to conclude that μ > 12.Reject H0. There is sufficient evidence to conclude that μ > 12.
(d)
What is the rejection rule using the critical value? (If the test is one-tailed, enter NONE for the unused tail. Round your answer to three decimal places.)
test statistic≤test statistic≥
What is your conclusion?
Do not reject H0. There is insufficient evidence to conclude that μ > 12.Do not reject H0. There is sufficient evidence to conclude that μ > 12. Reject H0. There is insufficient evidence to conclude that μ > 12.Reject H0. There is sufficient evidence to conclude that μ > 12.
Answers
a) Value of the test statistic is 1.54.
b) Range for the p-value is: 0.050 < p-value < 0.100
c) Do not reject H0. Due to insufficient evidence to get a result that μ > 12.
d) Do not reject H0. Due to insufficient evidence to get a result that μ > 12.
What is brief explaination to each part of the question?(a) To compute the value of the test statistic, we use the formula:
t = (x - μ) / (s / √n)
where;
x is sample mean
μ is hypothesized population mean
s is sample standard deviation
n is sample size.
Plugging in the given values, we get:
t = (14 - 12) / (4.54 / √25) ≈ 1.54
So the value of the test statistic is 1.54.
(b) To compute the p-value, we need to find the area under the t-distribution curve to the right of the test statistic. Using a t-table with 24 degrees of freedom (df = n - 1 = 25 - 1 = 24), we find that the closest value to 1.54 is 1.711.
The area to the right of 1.711 is between 0.05 and 0.10, so the range for the p-value is:
0.050 < p-value < 0.100
(c) At α = 0.05, the p-value (0.050 < p-value < 0.100) is greater than α, so we do not reject the null hypothesis. The conclusion is:
Do not reject H0. Due to insufficient evidence to get a result that μ > 12.
(d) The rejection rule by using of the critical value is:
If t ≤ tα,df, reject H0.
If t > tα,df, do not reject H0.
At α = 0.05 and df = 24, the critical value (from a t-table) is 1.711. Since the calculated test statistic (1.54) is less than the critical value (1.711), we do not reject the null hypothesis. The conclusion is the same as in part (c):
Do not reject H0. Due to insufficient evidence to get a result that μ > 12.
Learn more about test statistic.
brainly.com/question/14128303
#SPJ11
Simplify: 3.2/0.4 •2• 0.4/0.1
option 1) 64
option 2) 16
option 3) 6.4
option 4) 1.6
Answers
Answer:
1
Step-by-step explanation:
3.2/0.4=8
8×2=16
16×0.4=6.4
6.4÷0.1=64
For what values of a and b is the line 4x y = b tangent to the parabola y = ax2 when x = 5?
Answers
The line 4x + y = 30 is tangent to the parabola \(\(y = \frac{2}{5}x^2\)\) at the point \(\((5, 25\left(\frac{2}{5}\right))\)\).
To determine the values of a and b such that the line 4x + y = b is tangent to the parabola \(\(y = ax^2\)\), we need to find the point of tangency.
Given that the line is tangent to the parabola, the point of tangency will have the same x value for both the line and the parabola.
Let's substitute x = 5 into both equations and equate them:
For the line:
\(\(4(5) + y = b \Rightarrow 20 + y = b \Rightarrow y = b - 20\)\)
For the parabola:
\(\(y = a(5)^2 \Rightarrow y = 25a\)\)
Since the point of tangency has the same x value, we have:
25a = b - 20
To find the values of a and b, we need additional information. Let's assume the line is tangent to the parabola at the point (5, 25a).
The slope of the line is given by the coefficient of x in its equation, which is 4. The derivative of the parabola at the point of tangency will also give us the slope of the tangent line.
The derivative of the parabola \(\(y = ax^2\)\) with respect to x is:
\(\(\frac{dy}{dx} = 2ax\)\)
Evaluating the derivative at x = 5, we get:
\(\(\frac{dy}{dx} = 2a(5) = 10a\)\)
Since the slope of the tangent line is 4, we have:
10a = 4
\(\(a = \frac{4}{10}\)\)
\(\(a = \frac{2}{5}\)\)
Substituting the value of 'a' back into the equation 25a = b - 20, we can solve for b:
\(\(25\left(\frac{2}{5}\right) = b - 20\)\)
10 = b - 20
b = 10 + 20
b = 30
Therefore, the parabola is tangent to the line 4x + y = 30 \(\(y = \frac{2}{5}x^2\)\) at the point \(\((5, 25\left(\frac{2}{5}\right))\)\).
Learn more about parabola on:
https://brainly.com/question/9201543
#SPJ11
Need Help here Please!

Answers
Answer:
Step-by-step explanation:

To solve the given equation \(\sf x - y = 4 \\\), we can perform the following calculations:
a) To find the value of \(\sf 3(x - y) \\\):
\(\sf 3(x - y) = 3 \cdot 4 = 12 \\\)
b) To find the value of \(\sf 6x - 6y \\\):
\(\sf 6x - 6y = 6(x - y) = 6 \cdot 4 = 24 \\\)
c) To find the value of \(\sf y - x \\\):
\(\sf y - x = - (x - y) = -4 \\\)
Therefore:
a) The value of \(\sf 3(x - y) \\\) is 12.
b) The value of \(\sf 6x - 6y \\\) is 24.
c) The value of \(\sf y - x \\\) is -4.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Consider the following exponential probability density function. f(x) = 1/3 4 e^-x/3 for x > 0a. Write the formula for P(x < x_0). b. Find P(x < 2). c. Find P(x > 3). d. Find P(x < 5). e. Find P(2 <.x <5).
Answers
\(P(x < x_0) = ∫_0^x_0 f(x) dx\) ,\(P(x < 2) = ∫_0^2 (1/3) 4 e^-x/3 dx = -4e^-2/3 + 4\) , \(P(x > 3) = 1 - P(x < 3) = 1 - ∫_0^3 (1/3) 4 e^-x/3 dx = e^-1\) , \(P(x < 5) = ∫_0^5 (1/3) 4 e^-x/3 dx = -4e^-5/3 + 4\) , \(P(2 < x < 5) = P(x < 5) - P(x < 2) = (-4e^-5/3 + 4) - (-4e^-2/3 + 4) = 4e^-2/3 - 4e^-5/3\)
are the required solutions probability density function.
a. The formula for P(x < x_0) can be obtained by integrating the probability density function f(x) from 0 to x_0:
\(P(x < x_0) = ∫_0^x_0 f(x) dx\)
b. To find P(x < 2), we can substitute x_0 = 2 into the formula above and evaluate the integral:
\(P(x < 2) = ∫_0^2 (1/3) 4 e^-x/3 dx = -4e^-2/3 + 4\)
c. To find P(x > 3), we can use the complementary probability:
\(P(x > 3) = 1 - P(x < 3) = 1 - ∫_0^3 (1/3) 4 e^-x/3 dx = e^-1\)
d. To find P(x < 5), we can again use the formula for P(x < x_0) and substitute x_0 = 5:
\(P(x < 5) = ∫_0^5 (1/3) 4 e^-x/3 dx = -4e^-5/3 + 4\)
e. To find P(2 < x < 5), we can use the cumulative distribution function:
\(P(2 < x < 5) = P(x < 5) - P(x < 2) = (-4e^-5/3 + 4) - (-4e^-2/3 + 4) = 4e^-2/3 - 4e^-5/3\)
In general, the exponential distribution is commonly used to model the time until an event occurs, such as the time between radioactive decays or the time until a customer arrives at a service station. The parameter 1/λ, where λ is the rate parameter, represents the average time until the event occurs. The exponential distribution has a memoryless property, which means that the probability of the event occurring in the next unit of time is independent of the time elapsed so far. This property makes the exponential distribution useful in many applications, such as queuing theory and reliability analysis.
To know more about exponential distribution click here:
brainly.com/question/28235111
#SPJ4
what is the value of x please help meee

Answers
Correct answer gets BRAINLIEST!

Answers
Answer:
i think it is the 3rd one hope this helps.
Step-by-step explanation:
Miguel bought 8 equally priced pens for $3.84
How much will 15 pens cost?
Answers
$0.48 x 15 = $7.20
Have a great day :)
$7.50
Explanations:
Since it’s equally cost, you want to divide the total amount of the 8 pens by 8. $3.84/8 is equal to $0.48. Next, you want to multiple 15 by $0.48, since each pen is 48 cents. Your total is gonna $7.50. Hope that helps!!
Can anyone answer these for me pls

Answers
Answer:
#7 can be simplified to -10 √15x -40 √5
#8 = -20 √6x +30x√2
#9 = 10x√6+3 √15xx
#10 = -20√6a -15 √2
Step-by-step explanation:
12. Which line is perpendicular to the line given below

Answers
Answer:
B) 3x - 4y = -28
Step-by-step explanation:
Perpendicular = 90 degree angle

Answer:
B) 3x - 4y = -28
What is the diameter of a circle that has a radius of 5.2 yards?
** Do not put yards
Answers
Answer:
6.4
Step-by-step explanation:
( 2 + 3 ) ^-1 x ( 2 ^-1 + 2^-1 )
Answers
Answer:
Step-by-step explanation:
\(\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\la\la\la\la\ddddddddddddddddddddddddddddddddcleverdddddd\ffffffffffffffffffffffffffffffffffffffff\pppppppppppppppppppppppppppppppppppp\ddddddddddddddddddd\displaystyle\ \Large \boxed{ \boxed{\boldsymbol{Rule : a^{-1}=\frac{1}{a} }}} \\\\\\\\ (2+3)^{-1} \times (2^{-1}+2^{-1}) = \\\\1)\ (2+3)^{-1}=5^{-1}=\frac{1}{5} \\\\2)\ 2^{-1}+2^{-1}=\frac{1}{2} +\frac{1}{2} } =1 \\\\3)\ \frac{1}{5} \cdot 1=\boxed{\frac{1}{5} }\)
If f(x)= -1x2+3, find f(1)
Someone help me, I'm so confused ;-;
Answers
Answer:
-1×(1)×2+3=1 This is the answer I think
Suppose that one of the medians of a triangle happens to be exactly half the length of the side to which it is drawn. What can be said about the angles of this triangle? Justify your response
Answers
If the median of a triangle is exactly half the length of the side to which it is drawn, then the triangle must be isosceles.
An isosceles triangle has two equal sides and two equal angles. The two equal angles are opposite the two equal sides. This means that if the median of a triangle is exactly half the length of the side to which it is drawn, then the triangle must have two equal angles.
Furthermore, since the triangle is isosceles, the two equal angles must add up to 180 degrees. Therefore, the two equal angles of the triangle must each measure 90 degrees. In other words, the triangle will have one right angle. This can be easily seen by looking at the triangle and noting that the two equal sides form a straight line across the triangle, creating a right angle.
In summary, if the median of a triangle is exactly half the length of the side to which it is drawn, then the triangle must be an isosceles triangle with two equal angles that add up to 180 degrees, each measuring 90 degrees. This means that the triangle will have one right angle.
Learn more about the median of a triangle:
brainly.com/question/883707
#SPJ4
1. Determine the value of x.
Please help
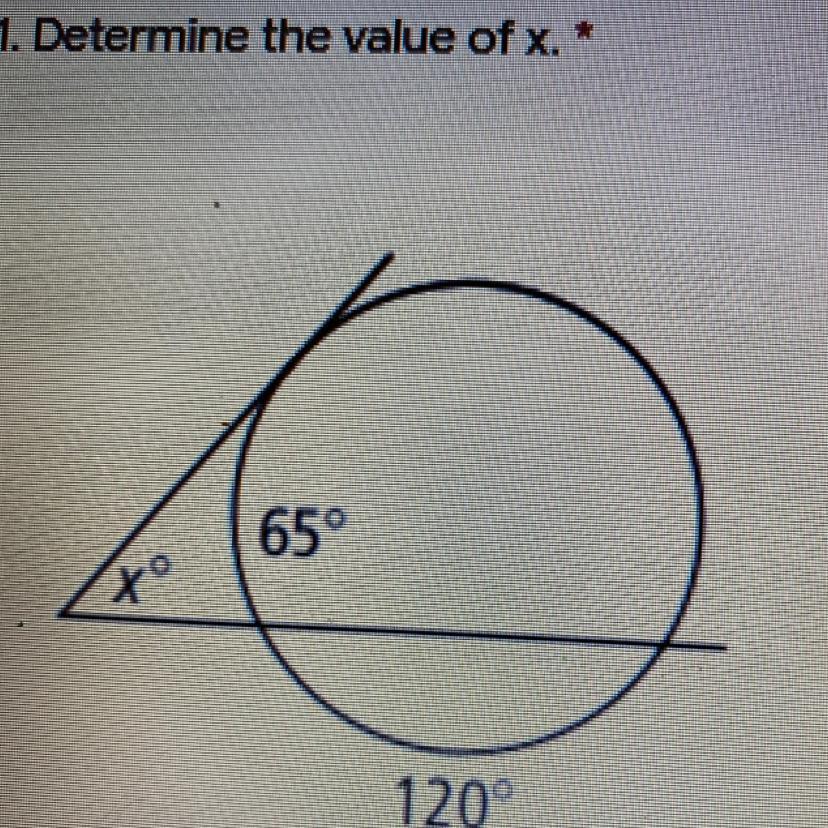
Answers
Answer:
55..........................
Consider the following function call round(3.14159, 3) what is the return value? a.3.14159 b.3.141 c.3.14 d.3.1
Answers
The return value of the function call round(3.14159, 3) is c. 3.14. The round function rounds the first argument (3.14159) to the number of decimal places specified in the second argument (3). In this case, it rounds to 3.14.
The function call in your question is round(3.14159, 3). The "round" function takes two arguments: the number to be rounded and the number of decimal places to round to. In this case, the number to be rounded is 3.14159 and the desired decimal places are 3.
The return value is the result of the rounding operation. In this case, rounding 3.14159 to 3 decimal places gives us 3.142.
So, the correct answer is:
b. 3.142
Visit here to learn more about function call:
brainly.com/question/25762866
#SPJ11
Find the best approximation to a solution of the following systems of equations. What the value for x? 4x 2y = 0 x +y = 11 -2 2 1
Answers
The best approximation to a solution of the system of equations is x = -11 and y = 22.
A system of equations is a collection of two or more equations with the same variables. Solving a system of equations means finding the values of the variables that satisfy all the equations in the system.
In this case, you have a system of two equations:
4x + 2y = 0 and x + y = 11.
To find the best approximation to a solution of the system, we can use substitution or elimination methods.
First, we can isolate one of the variables in one of the equations.
=> 4x + 2y = 0.
Dividing both sides by 2, we get:
=> 2x + y = 0.
Now we have one equation in terms of one variable, which is y.
Next, we can substitute the expression for y from this equation into the second equation:
=> x + y = 11.
Replace y with -2x
=> x + (-2x) = 11.
=> -x = 11.
=> x = -11.
Finally, we can substitute the value for x back into one of the original equations to find the value of y.
Let's substitute x = -11 into the first equation:
=> 4(-11) + 2y = 0.
=> -44 + 2y = 0.
=> 2y = 44.
=> y = 22.
To know more about equation here.
https://brainly.com/question/10413253
#SPJ4
The volume of a cone with height 29 cm is 1758 CM3, find the radius of the conw
Answers
Answer:13.77 cm.
Step-by-step explanation:
r = sqrt((3V)/(pih))
= sqrt((31758)/(pi29))
= sqrt((5274)/(pi*29))
= sqrt(182.16)/(pi/29)
= 13.77 cm
Need Help ASAP I cant solve this I think the answer might be 14x-35 but im not sure and i have to solve by combining like terms

Answers
In the attached diagram the perimeter of the hall way is
17x - 34How to find the perimeter of the hallwayThe perimeter of the hall way is calculated by adding all the sides of the hallway
The perimeter of the hall way = 2x - 7 + x + 1 + 4x - 9 + x - 2 + x + 2 + 3x - 11 + x - 2 + 3x - 11 + x + 4
adding like terms results to
The perimeter of the hall way = 17x + (-34)
Finally, the simplified expression is:
17x - 34
Learn more about perimeter at
https://brainly.com/question/19819849
#SPJ1
A company made 700000 profit last year. It says this was 12percent more than the year before. What was the profit made the year before
Answers
Answer:
784000
Step-by-step explanation:
Given data
Profit = 700000
Let us begin by finding what 12% of 700000 is
=12/100* 700000
=0.12* 700000
=84000
Hence the profit made last years was
=84000+700000
=784000
Please help me show my work. I know the answer, but don't know how to get to it.
Fiona is purchasing a condominium and is financing $305,000 with a 30-year 5/1 ARM at 4. 65% with a 1/12 cap structure. What will her payments be at the beginning of year 6?
Answers
Fiona's payment at the beginning of year 6 will be $110,977.32. The monthly payment is the amount of money that is due each month to pay off a loan.
To determine Fiona's payments at the beginning of year 6, we need to first calculate the monthly payment for the loan using the following formula:
Monthly Payment =\([P * R] / [1 - (1 + R) ^ (^-^N^)]\)
Where:
P = the loan amount (in this case, $305,000)
R = the monthly interest rate (in this case, 4.65%/12 = 0.0039583)
N = the number of monthly payments (in this case, 30 years x 12 months/year = 360 months)
Plugging these values into the formula, we get:
Monthly Payment = [$305,000 x 0.0039583] / [1 - (1 + 0.0039583) ^ (-360)]
= $1,534.61
To determine the payment at the beginning of year 6, we need to calculate the total number of payments that have been made up until that point. Since the payments are made monthly, at the beginning of year 6 there will have been 6 years x 12 months/year = 72 payments.
Therefore, Fiona's payment at the beginning of year 6 will be $1,534.61 x 72 = $110,977.32.
Learn more about payment, here https://brainly.com/question/15136793
#SPJ4
What is the answer to this question?

Answers
Answer:
A
Step-by-step explanation:
Use the drop-down menus to complete each equation so the statement about its
solution is true.

Answers
Answer:
Step-by-step explanation:

What is the height of the brick?

Answers
The height of the cube brick is 7 units and the volume is equal to 343 unit³
Volume of a cubeThe volume of a cube is defined as the total number of cubic units occupied by the cube. The formula is given as V = a³ where "a" is the length of edge or sides.
The length of an edge for the cube brick is 7 units which implies the height represented by h is also 7 units and the volume is calculated as follows:
volume of cube brick = 7 units × 7 units × 7 units
volume of cube brick = 343 units ³
Therefore, the height of the cube brick is 7 units and the volume is equal to 343 unit³
Learn more about volume of cube here: https://brainly.com/question/1972490
#SPJ1
can someone solve this and include the steps its due today!!!!!

Answers
Answer: x = 5
Use cross multiplication: A/B = C/D ⇒ AD = BC
(2x-5)/(3) = (x+5)/(6)
6(2x-5) = 3(x+5)
12x-30 = 3x+15 (Group the like terms)
12x-3x = 15+30
9x = 45 (Divide both sides by 9 to isolate for x)
x = 5
Answer:
x=5
Step-by-step explanation:
3x+15=12x-30>>>>9x=45>>>>x=5
The number of square units occupied by the space inside the circle. the word starts with A
Answers
The number of square units occupied by the space inside the circle is called area
The number of square units occupied by the space inside a circle is given by the formula A = πr^2, where A is the area of the circle and r is the radius. The letter A is commonly used to represent area in mathematical equations. The formula states that the area of a circle is proportional to the square of its radius, meaning that as the radius increases, so does the area. The constant π, which is approximately equal to 3.14, represents the ratio of the circumference of a circle to its diameter.
The area of a circle can be used in many real-world applications, such as calculating the amount of space inside a circular room or the amount of material needed to cover a circular surface.
Learn more about area here
brainly.com/question/28642423
#SPJ4
Instructions: Find the missing side lengths. Leave your answers as radicals in simplest form.

Answers
Answer:
\( a = 4 \)
\( b = 2\sqrt{3} \)
Step-by-step explanation:
✔️Solving for a using trigonometric ratio:
reference angle = 60°
hypotenuse = a
adjacent = 2
Thus:
\( cos(60) = \frac{2}{a} \)
\( \frac{1}{2} = \frac{2}{a} \) (cos 60 = ½)
Cross multiply
\( 1*a = 2*2 \)
\( a = 4 \)
✔️Solving for b using trigonometric ratio:
reference angle = 60°
Opposite = b
Adjacent = 2
Thus:
\( tan(60) = \frac{b}{2} \)
Multiply both sides by 2
\( tan(60)*2 = \frac{b}{2}*2 \)
\( tan(60)*2 = b \)
\( \sqrt{3}*2 = b \) (tan 60 = √3)
\( 2\sqrt{3} = b \)
\( b = 2\sqrt{3} \)
Find an ordered pair (x, y) that is a solution to the equation.
-x+5y=3
Answers
The ordered pair that is the solution to the equation -x + 5y = 3 is (-3,0) and (0, 0.6)
Ordered pair:
Ordered pairs refers a set of 2 numbers that exist in a particular order. The first one represents the x value and the second one refer the y value.
Given,
Here we need to find the ordered pair (x, y) that is a solution to the equation -x + 5y = 3
In order to find the solution ordered pair we have to plot this equation on the graph.
To plot this equation, we have to use the graphing calculator, and then input the given equation as the function, then we get the graph like the following.
While we looking into the graph, we have identified that the solution ordered pairs are (-3,0) and (0, 0.6)
To know more about Ordered pair here.
https://brainly.com/question/28874341
#SPJ1
