what is the equation of the line that is parallel to the given line and passes through the point (-3, 2)
• 3x-4y = -17
• 3x - 4y = -20
• 4x + 3y = -2
•4x + 3y = -6

Answers
Answer:
Parallel lines have the same slope. Find the slope of the "given" line
and then find the equation of the line with that same slope through (-3, 2)
Example: Find equation of the line parallel to y = -5x +4 through (-3, 2)
Slope of y = -5x + 4 is m = -5
Equation of line with slope -5 through (-3, 2)
y = -5x + b
2 = -5(-3) + b
2 = 15 + b
-13 = b
plz rate it and like
Related Questions
Hi again could you help me please
Find the area of the composite shape.

Answers
Answer:
For the one on the far left its 104 m2
Step-by-step explanation:
u split the shape in a square and rectangle
them u fin the area of the square by multiplying both sides. (8*8)
then u find the area of the rectangle by using the formula
2*(16+4)
when u find both areas u count them up and it'll become 104 m squared
Let U = {(x, y, z) € R^3 | x + 2y – 3z =0}. a) (2pt) Show directly (by verifying the conditions for a subspace) that U is a subspace of R^3. You may not invoke results learned in class or from the notes. b) (2pts) Find a basis for U. You must explain your method. c) (1pt) Using your answer from part b) determine Dim(U).
Answers
a) U is subspace of R^3.
b) The set {(3, -2, 0), (0, 1/2, 1)} is a basis for U.
c) 2.
a) To show that U is a subspace of R^3, we need to verify the following three conditions:
i) The zero vector (0, 0, 0) is in U.
ii) U is closed under addition.
iii) U is closed under scalar multiplication.
i) The zero vector is in U since 0 + 2(0) - 3(0) = 0.
ii) Let (x1, y1, z1) and (x2, y2, z2) be two vectors in U. Then we have:
x1 + 2y1 - 3z1 = 0 (by definition of U)
x2 + 2y2 - 3z2 = 0 (by definition of U)
Adding these two equations, we get:
(x1 + x2) + 2(y1 + y2) - 3(z1 + z2) = 0
which shows that the sum (x1 + x2, y1 + y2, z1 + z2) is also in U. Therefore, U is closed under addition.
iii) Let (x, y, z) be a vector in U, and let c be a scalar. Then we have:
x + 2y - 3z = 0 (by definition of U)
Multiplying both sides of this equation by c, we get:
cx + 2cy - 3cz = 0
which shows that the vector (cx, cy, cz) is also in U. Therefore, U is closed under scalar multiplication.
Since U satisfies all three conditions, it is a subspace of R^3.
b) To find a basis for U, we can start by setting z = t (where t is an arbitrary parameter), and then solving for x and y in terms of t. From the equation x + 2y - 3z = 0, we have:
x = 3z - 2y
y = (x - 3z)/2
Substituting z = t into these equations, we get:
x = 3t - 2y
y = (x - 3t)/2
Now, we can express any vector in U as a linear combination of two vectors of the form (3, -2, 0) and (0, 1/2, 1), since:
(x, y, z) = x(3, -2, 0) + y(0, 1/2, 1) = (3x, -2x + (1/2)y, y + z)
Therefore, the set {(3, -2, 0), (0, 1/2, 1)} is a basis for U.
c) Since the basis for U has two elements, the dimension of U is 2.
Learn more about subspace
brainly.com/question/30318872
#SPJ11
Which of the following is the function for the graph shown?

Answers
Answer: A. \(y = x^{2} + 6x + 8\)
Step-by-step explanation:
You can plug in the know point of (-3, -1) to each equation to see which one fits. The correct one in this case is \(y = x^{2} + 6x + 8\)
Is this function linear or nonlinear? y=2x2−4 nonlinear linear
Answers
Answer:
yes cause its in a form of y=mx+b
Step-by-step explanation:
Answer:
linear
Step-by-step explanation:
I got to K-12 and this was correct
Whoever answers correctly gets BRAINLIESTand 100 points
A rectangular prism with a length of 3.8 meters and a width of 1.5 meters has a volume of 16.53 cubic meters.
What is the height of the prism?
2.9 m
6.525 m
11.23 m
21.83 m
Answers
Answer:
2.9 meters.
Step-by-step explanation:
First we multiply the length, 3.8, by the width, 1.5, to get the base, 5.7 (this step is not entirely necessary, but makes it much easier). Then we divide the volume, 16.53, by the base, 5.7, to get the height, 2.9 meters.
Answer:
i think its 21.83 i may be wrong but im pretty sure its 21.83
Step-by-step explanation:
Find the average value of the function f(x, y) over the plane region R. f(x, y) = 6x^2y^3; R = {(x, y) | 2 ≤ x ≤ 4 ; 0 ≤ y ≤ 3
Answers
The average value of function f(x, y) over R is 512/5.
To find the average value of the function f(x, y) = 6x^2y^3 over the region R = {(x, y) | 2 ≤ x ≤ 4 ; 0 ≤ y ≤ 3}, we need to compute the double integral of f(x, y) over the region R and divide by the area of R.
The double integral of f(x, y) over R is:
∬R f(x, y) dA = ∫2^4 ∫0^3 6x^2y^3 dy dx
Evaluating this integral, we get:
∫2^4 ∫0^3 6x^2y^3 dy dx = ∫2^4 [3x^2y^4]0^3 dx
= ∫2^4 3x^2(3^4) dx
= (3/5)(4^5 - 2^5)
= 3072/5
The area of R is:
Area(R) = ∫2^4 ∫0^3 dy dx = (4-2)(3-0) = 6
Therefore, the average value of f(x, y) over R is:
(1/Area(R)) * ∬R f(x, y) dA = (1/6) * (3072/5) = 512/5
To learn more about function here:
https://brainly.com/question/12431044
#SPJ4
Find the value of the monomial: 3x^2y for x=1, y=9
Answers
Answer:
Step-by-step explanation:
3x^2y
3(2)^2(9)
6^18= 101 559 956 668 416
Answer:
387,420,489 is the answer to the monomial.
Step-by-step explanation:
3x^2y = 3(1)^2(9) when the variables are replaced.
3(1) = 3
2(9) = 18
3^18 = 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3
3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 387,420,489
Therefore, 387,420,489 is the answer to the monomial.
Hope this helps! :D
need help with these 2 questions
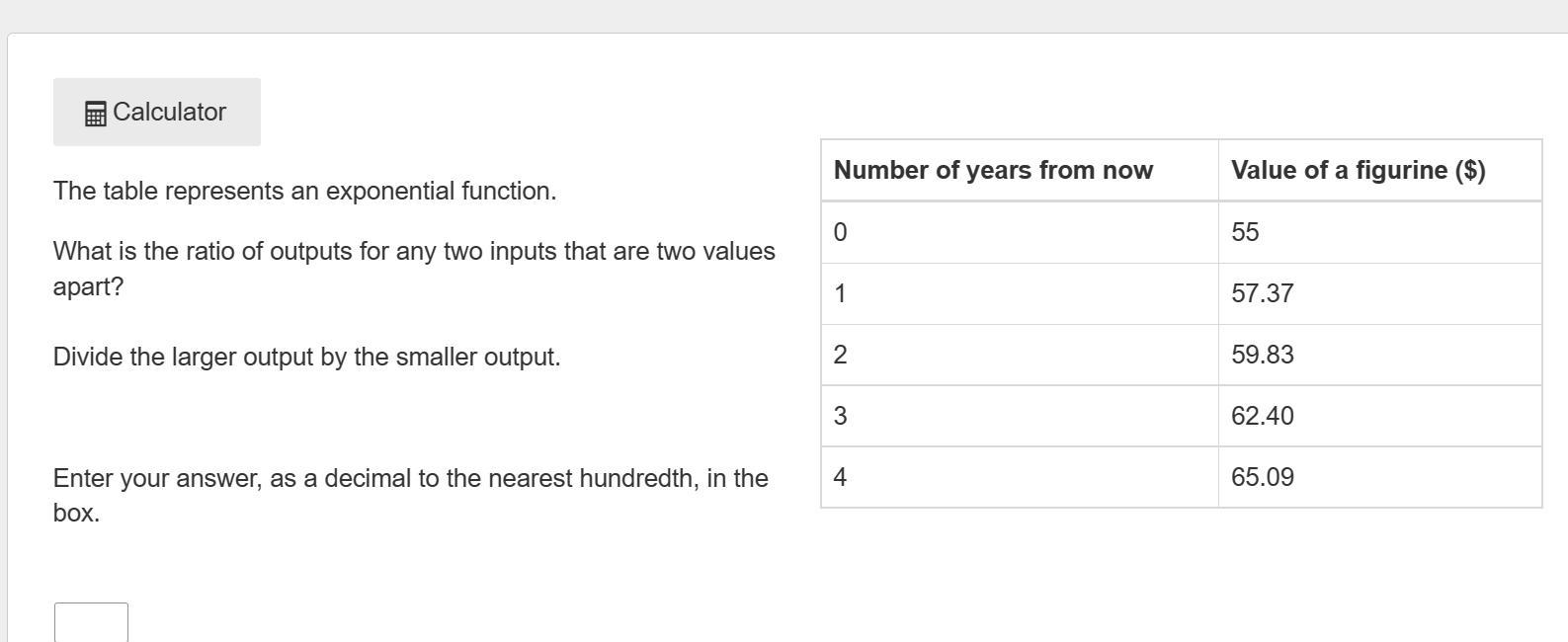

Answers
The ratio of output that are two values apart is 1.09.
Q2: the function for the given table is exponantial.
What is an exponential function?A mathematical function with the form f (x) = axe is an exponential function. "x" is a variable, while "a" is a constant that serves as the function's base and must be bigger than 0. The transcendental number e, or roughly 2.71828, is the base for exponential functions that are most frequently utilized.
Given table is an exponential function,
Number of years from now Value of a figurine ($)
0 55
1 57.37
2 59.83
3 62.40
4 65.09
to find the ratio of output that are two values apart,
to find the ratios of 59.83:55,
62.40:57.37, and 65.09:59.83
since the function is exponential the ratios are in proportion and ratio is equal,
59.83/55 = 62.40/57.37 = 65.09/83 = 1.09.
ratio is 1.09.
Q2
X f(x)
-5 8192
-3 512
-1 32
1 2
3 1/8
to find whether the functions are linear or exponential,
From the given table it is noticed that the rate of change is not constant, therefore it is not a linear function,
The general form of an exponential function is
y = abˣ
From the given table it is noticed that the function passes through the points (1,2) and (3, 1/8). It means the equation must be satisfied by these points.
2 = ab¹
1/8 = ab³
solving the equation we get,
b = 1/4
and a = 8
equation = y = 8(1/4)ˣ
checking the points,
f(-5) = 8(1/4)⁻⁵ = 8192
f(-3) = 8(1/4)⁻³ = 512
f(1) = 8(1/4)¹ = 2
so the function is exponential.
Hence, the ratio for the terms is 1.09.
Q2: te function is exponential.
Learn more about exponential function;
https://brainly.com/question/14355665
#SPJ1
Bob is planning to start an it business, servicing computers that are infected with viruses. to start his new enterprise, bob estimates that he will need to spend $5,000 on equipment $6,000 on premises, $4,000 on advertising. all of these costs are fixed. he is planning on charging his customers $250 each to fix an infected computer. for each computer that he fixes, he must spend $25 on parts and software. suppose we let x be the number of computers that bob fixes. if bob only fixes 50 computers, what is his total loss?
Answers
If Bob only fixes 50 computers, his total loss is $3,750.
What is the total loss?The total loss results from the negative difference between the total revenue and the total costs.
The total costs consist of variable and fixed costs.
The result is a loss when the total costs exceed the total revenue. This result becomes a profit or income when the total revenue exceeds the total costs.
Fixed Costs:Equipment = $5,000
Premises = $6,000
Advertising = $4,000
Total fixed costs = $15,000
Variable cost per unit = $25
Selling price per unit = $250
Total number of computers fixed = 50
The total variable cost for 50 units = $1,250 (50 x $25)
The total costs (fixed and variable) = $16,250
The sales revenue for 50 units = $12,500 (50 x $250)
Loss = $3,750 ($12,500 - $16,250)
Thus, Bob will incur a total loss of $3,750 if he fixes only 50 computers based on his fixed and variable costs.
Learn more about fixed and variable costs at https://brainly.com/question/14872023
#SPJ1
3 Jazmin is mailing two packages. One package weighs 3 pounds, and the other package weighs 20 ounces. What is the total weight of both packages? (1 pound = 16 ounces)
Answers
Answer:
68oz
Step-by-step explanation:
1) 3lbs x 16oz = 48
Now we know 3lbs is 48oz. since one pound is 16 ounces, 3 pounds is 48 ounces.
2) 48 + 20 = 68oz
3) The total weight of both packages is 68 ounces.
Jesus loves ya, have a great day!
---------------------
John 8:12 - When Jesus spoke again to the people, he said, "I am the light of the world. Whoever follows me will never walk in darkness, but will have the light of life."
HURRY ANSWER QUICKLYYYY!!!!!!Angle APE and angle EPD are congruent. Find the measure of minor arc BE?

Answers
The measure of the minor arc BE is 104⁰.
What are congruent angles?
Congruent angles are two or more angles that are identical to each other. Thus, the measure of these angles is equal to each other.
This implies that;
∠APE = ∠ EPD = x
2x + 55 + 41 + 166 = 360 ( sum of angles in a circle)
2x + 262 = 360
2x = 98
x = 98 / 2
x = 49⁰
The measure of the minor arc BE is calculated as;
BE = 55⁰ + 49⁰
BE = 104⁰
Learn more about minor arc here: https://brainly.com/question/23498567
#SPJ1
Hiiioo! Can someone please help me out! :)❤️

Answers
Answer:
-2/3
3/2
Step-by-step explanation:
slope is m in the equation y = m*x+b.
3y=-2x-3
y=-2/3x-1
parallel lines have the same slope, so slope of parallel lines is -2/3
perpendicular lines have negative the inverse
so -(-3/2)=3/2
A dependent variable is the variable that we wish to predict or explain in a regression model. True False
Answers
True. In a regression model, the dependent variable is the variable that we aim to predict or explain using one or more independent variables.
In a regression model, the dependent variable is indeed the variable that we aim to predict or explain. It represents the outcome or response variable that we are interested in understanding or analyzing. The purpose of the regression analysis is to examine the relationship between this dependent variable and one or more independent variables. By identifying and quantifying the influence of the independent variables on the dependent variable, regression analysis allows us to make predictions or explanations about the behavior or value of the dependent variable.
The regression model estimates the relationship between the variables based on observed data and uses this information to infer how changes in the independent variables impact the dependent variable.
To learn more about variable , click here:
brainly.com/question/29583350
#SPJ1
Parametrize the portion of the cone z- V8x2 + 8y2 with 0 s zs V8. (Your instructors prefer angle bracket notation>for vectors.)
Answers
The parametric equations for the portion of the cone are: r(t) = t, θ(t) = t, z(t) = 2√2t where t is a parameter that ranges from 0 to √8.
To parametrize the portion of the cone z - √(8x^2 + 8y^2) with 0 ≤ z ≤ √8, we can use cylindrical coordinates. Let's denote the parameters as r, θ, and z.
We know that x = rcosθ, y = rsinθ, and z = z.
Substituting these values into the equation of the cone, we have:
z - √(8(rcosθ)^2 + 8(rsinθ)^2) = 0
Simplifying the expression inside the square root, we get:
z - √(8r^2(cos^2θ + sin^2θ)) = 0
z - √(8r^2) = 0
z - 2√2r = 0
From this equation, we can express z in terms of r as:
z = 2√2r
Know more about parametric equations here:
https://brainly.com/question/28537985
#SPJ11
Select ALL figures for which at least one cross section is a circle.
O triangular pyramid
O square pyramid
Orectangular prism
cube
Ocone
O cylinder
Osphere
Answers
the correct options are:
O cone
O cylinder
O sphere
What is cylinder?
A cylinder is a three-dimensional geometric shape that consists of two parallel circular bases that are connected by a curved lateral surface. It is a type of prism, as the cross-section of a cylinder taken perpendicular to its axis is always the same, and is a circle.
The volume of a cylinder is calculated as the product of the height (h) and the area of the base (B), which is a circle with radius (r). Therefore, the volume of a cylinder is given by the formula:
V = Bh = πr²h
To know more about cylinder related questions visit:
https://brainly.com/question/16134180
#SPJ1
How long will it take for a $3000 investment to grow to $6450 at an annual rate of 10%, compounded quarterly? Assume that no withdrawals are made. Do not round intermediate computations, and round your answer to the nearest hundreth
Answers
It will take approximately 4.1 years for a $3000 investment to grow to $6450 at an annual rate of 10%, compounded quarterly.
What is compound interest?The interest that is accrued on both the principle and any accumulated interest from earlier periods is known as compound interest. In other words, interest is gained on top of interest and is reinvested. With time, compound interest increases enormously.
Simple interest, on the other hand, is interest that is simply paid on the principle. As interest is not reinvested, the investment's growth is linear over time.
The compound interest is given by the formula:
\(A = P(1 + r/n)^{(nt)}\)
Substitute the values given:
\(A = $3000(1 + 0.10/4)^{(4t)}\\$6450 = $3000(1 + 0.10/4)^{(4t)}\\2.15 = (1 + 0.10/4)^{(4t)}\)
Taking log on both sides we have:
\(ln(2.15) = ln[(1 + 0.10/4)^{(4t)]}\)
ln(2.15) = 4t ln(1 + 0.10/4)
t = ln(2.15)/(4 ln(1 + 0.10/4))
t ≈ 4.1
Hence, it will take approximately 4.1 years for a $3000 investment to grow to $6450 at an annual rate of 10%, compounded quarterly.
Learn more about compound interest here:
https://brainly.com/question/29335425
#SPJ1
The two-way frequency table shows the results of a survey of students.
Right-handed
Left-handed
Total
In music program Not in music program Total
43
394
437
15
33
48
427
475
OA. 48
58
How many left-handed students are not in the music program?
Answers
The given two-way Frequency table, there are 33 left-handed students who are not in the music program.
The number of left-handed students who are not in the music program, we need to examine the data presented in the two-way frequency table.
From the table, we can see that the number of left-handed students in the music program is 15, and the total number of left-handed students is 48.
the number of left-handed students not in the music program, we subtract the number of left-handed students in the music program from the total number of left-handed students.
Number of left-handed students not in the music program = Total number of left-handed students - Number of left-handed students in the music program
Number of left-handed students not in the music program = 48 - 15
Calculating this, we find that the number of left-handed students not in the music program is 33.
Therefore, there are 33 left-handed students who are not in the music program, based on the data provided in the two-way frequency table.
In conclusion, based on the given two-way frequency table, there are 33 left-handed students who are not in the music program.
To know more about Frequency .
https://brainly.com/question/28821602
#SPJ8
Find the area of the figure below.

Answers
I am stuck on this too...
Maybe we can figure it out together
can someone please help with this???

Answers
Answer: Associative property
Answer:
yes
Step-by-step explanation:
its D
If the matrix of coefficients of a system of n linear equations in n unknowns is singular, then the system has infinitely many solutions. (a) Always true (b) Sometimes true (c) Never true, (d) None of the above
Answers
A system of n number of linear equations in n unknowns has an many number of solutions if the coefficients of matrix is unique. The assertion is always accurate. The given statement is always true.
From the question, the given statement is:
A system of n linear equations in n unknowns has an endless number of solutions if the matrix of coefficients is unique. The assertion is always accurate.
The given statement is always true.
Consider the system of equations Ax = b. If A is single, there is no A-inverse. As a result, there is no one approach to solve the system. Then, there are still two options:
There are countless options.No answers.We can't tell which condition is right only examining the matrix [A b]. There exists an endless number of solutions if [A b] is equal to A's rank.
To learn more about linear equations link is here
brainly.com/question/28464514
#SPJ4
3. (07.05 MC) An equation is shown below: 12x + 3(x - 5) = 6x + 9x - 15
Part A: Solve the equation and write the number of solutions. Show all the steps. (6 points)
Part B: Name one property you used to solve this equation. (4 points)
Answers
The equation 12x + 3(x - 5) = 6x + 9x - 15 has infinite many solutions
Solving the equationPart A:
Starting with the given equation:
12x + 3(x - 5) = 6x + 9x - 15
Simplify by distributing the 3:
12x + 3x - 15 = 6x + 9x - 15
Combine like terms on both sides:
15x - 15 = 15x - 15
Add 15 to both sides:
0 = 0
Therefore, the equation has infinite many solutions
Part B:
The property used to solve this equation is the distributive property of multiplication over addition, which states that a(b + c) = ab + ac. In this case, we used the distributive property to simplify 3(x - 5) to 3x - 15.
Read more about equation at
https://brainly.com/question/148035
#SPJ1
Simplify.
100x(5 - 3p)
500x - 3p
5x - 300p
500x - 300p
500x - 300px
giving brainliest
help me pleaseeeeeeeeeeeeeee
Answers
Answer:
=500x^2-300px
Step-by-step explanation:
The problem asks us to simplify,
We can simplify by using the distributive property,
100x(5x-3p)
Distribute 100x inside,
100x*5x=500x^2 (x*x=x^2)
100x(-3p)=-300px (positive x negative = negative)
\(100x*5x=500x^2\\\\ 100x*-3p=-300px \\\\=500x^2-300px \\\)
At any time t > 0,the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized ad tlie number of words tlat have not been memorized. If 2 denotes the number of words memorized at time t, which differential equation models this situation? Assume kis a positive constant; A. d k dt B. d k ( - M) dt C d k(M - 2) dt D. d =Rt(M -t) dt
Answers
The differential equation that models this situation is dx/dt = kx(M - x) (option c).
To determine the differential equation that models the situation, let's analyze the problem statement.
The rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized.
Let's denote the number of words memorized as "a" and the number of words not yet memorized as "M - a" (where M is the total number of words in the list).
The problem states that the rate of memorization is proportional to the product of "a" and "M - a". We can express this mathematically as:
Rate of memorization ∝ a * (M - a)
To convert this proportionality into an equation, we introduce a positive constant k:
Rate of memorization = k * a * (M - a)
The left side of the equation represents the rate of change of the number of words memorized (da/dt), and the right side represents the product of "a" and "M - a" multiplied by the constant k.
Therefore, the differential equation that models this situation is:
da/dt = k * a * (M - a)
Comparing this with the given options, we can see that the correct choice is option C:
dx/dt = k * x * (M - x)
The complete question is:
At any time t > 0 the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized. If a denotes the number of words memorized at time t, which differential equation models this situation? Assume k is a positive constant.
A. dx/dt = kx
B. dx/dt = kx(x - M)
C. dx/dt = kx(M - x)
D. dx/dt = kt(M - t)
To know more about differential equation:
https://brainly.com/question/32524608
#SPJ4
help me with b and you get brilliant

Answers
Hello,
\( \frac{10000 \times 6}{10} \)
\(6000\)
Therefore, 6000 will be your answer.
Benjemin
evaluate 6+4/a+b/3 when a=4 and b=3
Answers
Answer:
8
Step-by-step explanation:
First, insert the values into the problem. It would look like this: 6 + 4/4 + 3/3
We can then reduce 4/4 into 1 and 3/3 into 1 as well.
Then, you get:
6+1+1 or 6+2 which is equal to 8
-Cheers, Galaxy
Solve step by step 249×625
Answers
Answer:
155625 is the answer.
Step-by-step explanation:
add astre#6666 on discord for the step by step
PLEASE HELP ME Check the picture and tell me whats the answer please

Answers
Answer:
B
Step-by-step explanation:
Given
(4x + 3)(3x - 4)
Each term in the second factor is multiplied by each term in the first factor, that is
4x(3x - 4) + 3(3x - 4) ← distribute both parenthesis
= 12x² - 16x + 9x - 12 ← collect like terms
= 12x² - 7x - 12
The coefficient of the x- term is - 7 → B
What is the length of AD?

Answers
Answer:
So, We Need To Write An Equation To Find This:
AD = lAl + lDl Step-by-step explanation:
AD = l-7l + l8l
l-7l= 7.
AD = 7 + 8
7+8 = 15
AD = 15 So, AD = 15. This Means That The Answer Is B.
∆ABC and ∆PQR are congruent under the correspondence: ABC ↔ RQP
then the part of ∆ ABC that correspond to:
Answers
Answer:
Please check the explanation.
Step-by-step explanation:
Given
ABC ↔ RQP
so
ΔABC ≅ ΔABC
It means the triangles are congruent.
Please check the attached diagram.
In the diagram,
A ↔ RB ↔ QC ↔ PParts of ΔABC that correspond to
(i) PQ
\(PQ\) corresponds to \(CB\)
(ii) ∠Q
∠Q corresponds to ∠B
(iii) RP
\(RP\) corresponds to \(AC\)

how many positive odd factors of 48 are greater than 2 and less than 10
Answers
Answer:
Just 1 positive, odd factor
Step-by-step explanation:
48 has many factors. But not many odd factors. Only 3 is odd and bigger than 2 and less than 10.
So, just one odd, positive factor.